考虑学习效应的新产品R&D项目组合调度模型研究

陈 蓉，梁昌勇，叶春森



考虑学习效应的新产品R&D项目组合调度模型研究

陈 蓉1,2，梁昌勇1,3，叶春森4

（1. 合肥工业大学管理学院，安徽合肥 230009；2. 合肥师范学院经济与管理学院，安徽合肥 230601；3. 合肥工业大学智能决策与信息系统技术教育部工程研究中心，安徽合肥230009;4.安徽大学商学院，安徽合肥 230601）

新产品研发项目组合管理的三个关键因素是人才、研发周期和成本。考虑多技能研发人员的学习效应，将技能增值作为一个主要目标，建立以技能增值、研发周期和成本为目标的新产品研发项目组合多目标调度模型。开发了基于NSGA-Ⅱ的改进算法来求解问题的非劣解集，通过赋予目标不同的权重来考虑决策者对各个目标的偏好，进一步根据理想解法从非劣解集中选出最佳调度方案。最后对合肥某电气公司的配网自动化监控终端新产品研发项目组合调度问题进行了实证分析，分析显示模型贴近企业实践，算法可行、有效，能够满足企业在进行新产品研发项目组合调度时的决策需求。

项目组合调度；多技能人配置；学习效应；多目标优化；新产品研发

0 引言

研发项目组合是企业为了实现新产品开发目标而集中放在一起以便进行有效管理的一组项目。面对当前科技的迅猛发展，产品生命周期不断缩短，全球化竞争加剧，采用组合管理理论与方法来有效管理新产品研发活动，能够帮助企业实现利润最大化、维持企业竞争地位、合理有效地分配稀缺资源等目标[1]。项目组合管理是企业成功开发新产品的基础，它是有关资源的分配，即公司如何分配资金和人力资源以及如何选择适当的投资项目[2]。

有关项目组合选择问题已经有不少研究成果[3~6]，而项目组合调度问题的研究还不多见。目前调度问题研究主要集中在单个项目和多项目管理中。其中，多技能人调度问题是研究的一个重点领域，由于科学技术的进步和人的学习能力的不断提升，使得当前研发项目调度面临一个项目需要多种技能、一个研发人员又具备多种技能的情况，形成了项目需求和人员技能之间的多对多选择关系，也即多技能人调度问题。Cai研究了三种类型技能人调度问题，建立了成本最小化、剩余员工最大化以及员工多样性最小化的三个目标优化模型，设计了遗传算法进行求解，该模型没有考虑多技能人的能力水平差异[7]；付方等考虑到多技能人的能力水平差异，建立了多项目环境下的单目标优化模型，采用列生成法对问题加以分解，再利用混合遗传算法进行优化，该模型没有考虑员工技能会随着时间增加而提升[8]；Wu和Sun根据学习曲线，提出员工的能力随着工作时间的增加而增长，建立了成本最小化的多项目人员调度模型并采用遗传算法进行求解，该模型仅考虑了单一技能和单个目标[9]。此外，上述文献都没有在项目组合背景下研究多技能人调度问题，且多以成本为决策目标。Walter首先建立了项目组合背景下人员调度的双目标优化模型，并采用P-ACO和NSGA-Ⅱ两种算法进行求解，该模型的主要贡献是除了考虑财务目标以外，还将研发人员技能增值最大化作为目标，以便在项目组合选择和人员调度过程中进行技能培养，提高公司的整体研发水平[10]。但是该模型没有考虑不同技能水平的员工完成相同任务的时间不同，并且人员安排方案不同会造成项目组合研发周期的不同，使得该模型不贴近企业实际情况，降低了模型的应用性。特别地，在新产品研发项目组合中研发周期是新产品上市成功的一个关键因素，时间的滞后可能使得研发出的新产品被竞争对手抢先推出，导致新产品的获利能力大打折扣。因此，新产品研发项目组合调度必须要考虑到研发周期这一目标，研发周期的长短直接决定新产品上市速度或者交付时间，进而影响公司新产品战略的成败。除了成本和周期两个常见目标以外，为了保证企业的战略地位，研发能力的提升也应作为一个很明确的目标。由于满足研发所需的特定能力不容易短期内从市场上招募到，即便招聘到新的员工，由于新员工融入企业研发团队产生的协作和交流成本很大，导致企业更倾向于从内部发展能力，然而内部发展也需要耗费成本和时间。因此，企业必须在日常的项目研发过程中通过不同人员调度方案进行人才梯队建设，培养关键性、稀缺性人才，提高企业研发能力，应对研发人员流失（辞职、跳槽）带来的人才危机。

综上所述，本文从实际应用角度出发，提出一种包括技能增值、时间和成本三个目标的新产品研发项目组合多技能人调度模型，并结合问题特征，提出了一种求解该模型的改进NSGA-Ⅱ算法，最后采用实例对模型与算法进行了实证分析。

1 学习曲线

学习曲线也称“熟练曲线”，最早由Wright[11]提出，他在研究飞机制造时间时得出，随着飞机产量的增加，飞机的制造时间随之降低，也即飞机的制造效率随产量递增，但当累计产量达到一定数量后，生产效率趋于稳定。随后学习曲线效应在各个领域展开研究，文献[12]对学习曲线的研究进行了综述。Wu和Sun首先在项目选择调度中将学习曲线理论应用于研究研发项目中研发人员的学习效率，认为研发人员使用某一技能的时间越长，其在该技能上的研发效率也会随之增长[9]。假设研发人员使用技能参与研发项目，其技能计算公式如下：

图1 学习曲线

2 问题建模

2.1 问题描述和假设

（1）不考虑人力资源外包，假设企业的现有研发人员数量和技能种类能够满足研发项目组合的需求；

（2）员工的工资为研发周期内的平均综合工资，包括月工资、福利和奖金在内，且不考虑没有参与研发的员工的机会成本；

（3）项目工期的计算只考虑依赖关系，不考虑时滞；

（4）员工技能的计算以项目为界限，不考虑单个项目研发过程中各个时点的技能变化；

（5）员工技能的增加符合学习曲线中的高原效应，也即企业内某种技能水平最高的员工在该技能上通过锻炼，技能不再提升或者提升较少以至于可忽略不计；

（6）在项目组合研发周期内，不考虑员工个体学习率差异以及遗忘效应对学习曲线的影响。

2.2 符号表示

2.2.1 参数

2.2.2 变量

2.3 目标函数

（2）

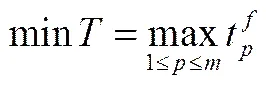
（4）

式（2）表示企业总技能增值最大化目标，总的技能增值等于所有参与项目的员工的所有技能增值之和；式（3）表示新产品研发周期最短化目标，研发周期为最迟完成的项目的终止时间；式（4）表示新产品研发成本最小化目标，总成本为所有参与项目的员工工资的总和。

2.4 约束条件

（6）

，（7）

（9）

if，（10）

（12）

（13）

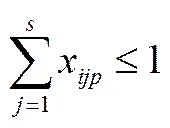
，（15）

，，，，（16）

3 模型求解

本模型包含三个决策目标：员工技能增值、研发周期和研发成本。模型中还含有非线性约束条件，为非线性约束多目标优化问题，也是典型的NP-hard问题。根据问题特征，本文设计了一种改进的NSGA-Ⅱ[13]算法进行求解,首先根据算法求出问题的非劣解集（Pareto解集），再进一步考虑决策者的偏好从所求非劣解集中选择最优方案。对于众多约束条件的处理，是问题求解的关键，算法中一部分约束条件通过个体编码、种群初始化等编程实现，另一部分约束条件通过不可行解修复和罚函数的方式在算法中实现。

3.1 个体编码和种群初始化

3.2 序值和拥挤距离计算[14]

个体序值通过循环排序进行计算。从1开始计算，每一轮循环增加序值1，在每一轮循环中将该轮循环中未被排序的个体与其余未被排序的个体进行比较，如不受其它个体支配，则被赋予当前循环的序值，否则参与下一轮排序。通过循环排序，每个个体都被赋予了相应的序值。拥挤度的计算分层进行，将序值相同的个体放在同一层进行计算。首先，对个体每一目标值进行升序排列；其次，每一个个体拥挤距离由该个体与其相邻前后两个个体之间的距离和表示，这里采用式（18）进行计算，将目标函数的两端极值的差作为分母可消除多个目标函数不同量纲的影响，位于两端的个体拥挤度赋值为1；最后再将个体在每一个目标值上计算的拥挤距离相加即可得到个体的总拥挤度。拥挤距离越大，种群多样性越好。

3.3 遗传操作

选择算子采用锦标赛方式进行，对选中的两个个体，按照序值和拥挤距离进行取舍，序值不同时选择序值小的个体，序值相同时选择拥挤距离大的个体。交叉算子采用单点交叉方式。变异算子通过随机选择染色体和变异位置进行变异操作。交叉算子能够提高算法的全局搜索能力，变异算子能够提高算法的局部搜索能力。分别编制子程序cross文件和mutation文件。由于模型中约束条件的存在，可能导致个体在交叉或变异后产生不可行解。因此，对于交叉和变异后产生的新个体需要进行约束检验，如检测出个体为不可行解，则进行调整或者惩罚处理。调整是对不可行解中个别不符合约束的人员安排进行重新选派，使其符合约束要求成为可行解。惩罚是将不可行解的适应值加上一个很大的数使其在下一轮选择中自然淘汰。

3.4 适应度函数

为提高结果的直观性，适应度函数直接采用员工技能增值、周期和成本的计算公式，编制程序function文件。其中，技能增值目标值越高，个体适应值越高；研发周期目标值越低，个体适应值越高；成本目标值越低，个体适应值越高。

3.5 约束处理

约束式（5）、（6）、（7）、（8）、（9）和（10）是对工期的计算，包括单个项目的工期以及项目组合的总周期，通过适应度函数程序function实现；约束式（11）、（12）和（16）是对技能增值的计算，可计算出每个员工在每一项技能上的增加值，也通过适应度函数程序function实现；约束式（15）是对同一时间段内员工参与时间的限制，在程序function中，对个体中存在同一员工同时参与两个以及两个以上项目的时间之和进行检验，如超过员工总时间的限制，采用惩罚值进行处理，即将该个体成本和周期目标加上一个大数M(M在数量级上超过成本、工期的范围)，同理将技能增值目标减去大数M。约束式（13）要求每个项目所需的每种技能有且只有一人负责，可通过个体编码和初始化种群程序popinitial文件实现。约束式（14）要求每一个员工不能采用两种及两种以上的技能参与同一项目，通过编制程序individualadjust文件实现，将同一项目中每种技能的参与人进行两两比较，如果得出参与人为两个不同的人则通过检验，否则，将其中一种技能的参与人换为具备该技能的其他员工。

3.6 最优方案决策

根据快速非支配遗传算法的思想可求出问题的非劣解集，而如何选取最优方案则需进一步决策。由于模型中三个目标受到公司本身的人才构成状况、新产品研发项目组合特征以及当前市场环境状况的不同程度影响，使得决策者对三个目标的偏好并不相同，这里引入偏好系数辅助决策。又考虑到三个决策目标量纲不同，引入理想点决策方法，通过计算相对接近度在求得的非劣解集中选择最优方案。相对接近度是指各非劣解方案与各目标的正负理想点之间的距离。正负理想点分别由非劣解集中的单目标最优值和最劣值表示。各方案与正负理想点之间的距离以及相对接近度的计算公式如下：

（20）

（21）

3.7 算法步骤

算法主程序具体步骤如下：

第1步：读取模型具体数据，设定遗传算法参数，包括进化代数、种群规模、交叉概率和变异概率。

第2步：调用子程序popinitial，生成初始种群，初始非劣解集为空集。

第3步：开始循环迭代，分别调用程序cross和mutation进行交叉和变异操作，程序cross和mutation中分别调用子程序individualadjust进行个体可行性检验。将交叉和变异后的个体及序值为1的非劣解合并到现有种群中，删除重复个体，并计算个体适应度。

第4步：对种群中的个体进行排序，并根据式（18）分层计算个体的拥挤度。根据序值和拥挤度选择个体生成新一代种群。

第5步：重复第3步和第4步，达到规定的进化代数之后，转入第6步。

第6步：输出模型的非劣解（序值为1），根据式（19）、（20）和（21）计算各非劣解的相对接近度，选择相对接近度最大的非劣解作为最优方案。

4 实例分析

C公司是坐落于合肥市高新区一家致力于配用电自动化、电力专网通信、运营商通信、工业生产机器人产品的研发、生产、销售以及工程技术服务的上市公司，公司掌握本行业最先进的核心技术。配网自动化监控终端是其主要产品之一，该产品主要用户为国家电网、南方电网等，主要作用是通过对配电设备的远程监控，消除故障隐患，减少故障的发生，快速抢修故障，减少停电范围，缩短停电时间，从而有效提高供电可靠性。以某配网自动化监控终端新产品研发项目组合为例，对模型进行实证分析。该项目组合包含10个子项目，子项目之间的先后关系见表1，共需研发技能8种，每一子项目需要其中的多种技能，各个技能是并行开工，每一项目所需技能及最短研发时间见表2。目前公司可供调度的员工有40名，员工工资见表3，每位员工所掌握的技能种类及初始水平见表4，各员工的初始技能水平由项目经理、研发主管和技术负责人等组成专家小组评价给出。根据公司的项目研发经验及时间记录，采用直接测定法，学习率取0.95。

表1 各子项目及其先后关系约束

表2 各项目研发技能的最短时间需求(单位：月)

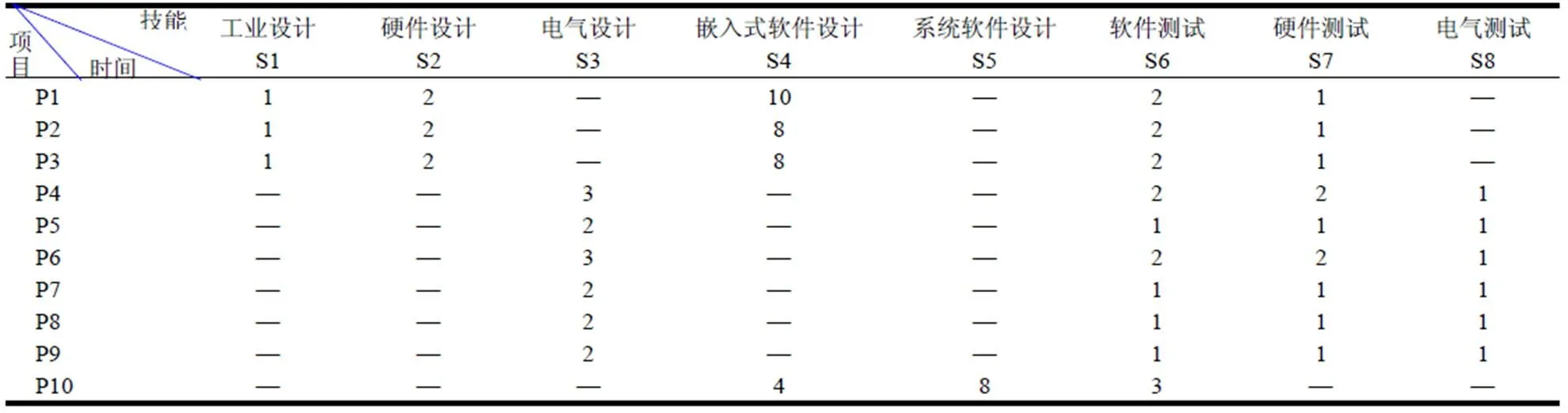
表3 员工工资（单位：元）

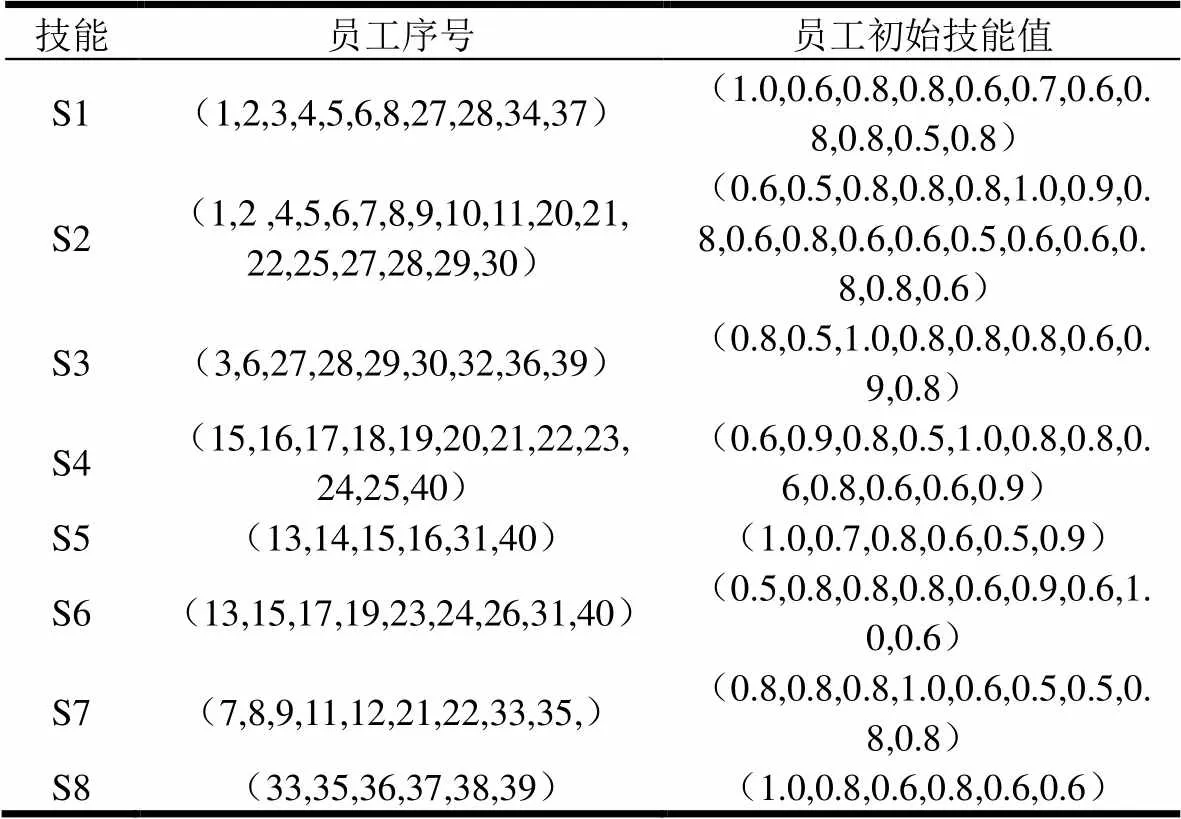
表4 掌握各技能的员工序号及其初始技能值

采用新产品研发项目组合多目标优化模型，利用本文设计的改进NSGA-Ⅱ算法，针对实例给出的问题进行求解，算法采用matlab软件，版本为R2010b，在Inte（R）Core（TM）i5-3470 cpu @3.20GHz计算机上运行。通过实验调整遗传算法各参数值，根据求解效果，设定遗传算法的种群规模为200，迭代次数为300，交叉概率为0.9，变异概率为0.3。经过多次试验,求解得出非劣解所构成的Pareto前沿如图2所示，可以看出该前沿的分布接近光滑曲面，反应了算法收敛性较好。进一步根据式（21），考虑新产品研发项目的市场竞争要求及公司人才战略，结合决策者偏好，设定、、，可以计算出各非劣解方案的相对贴近度，进一步选出最优方案。

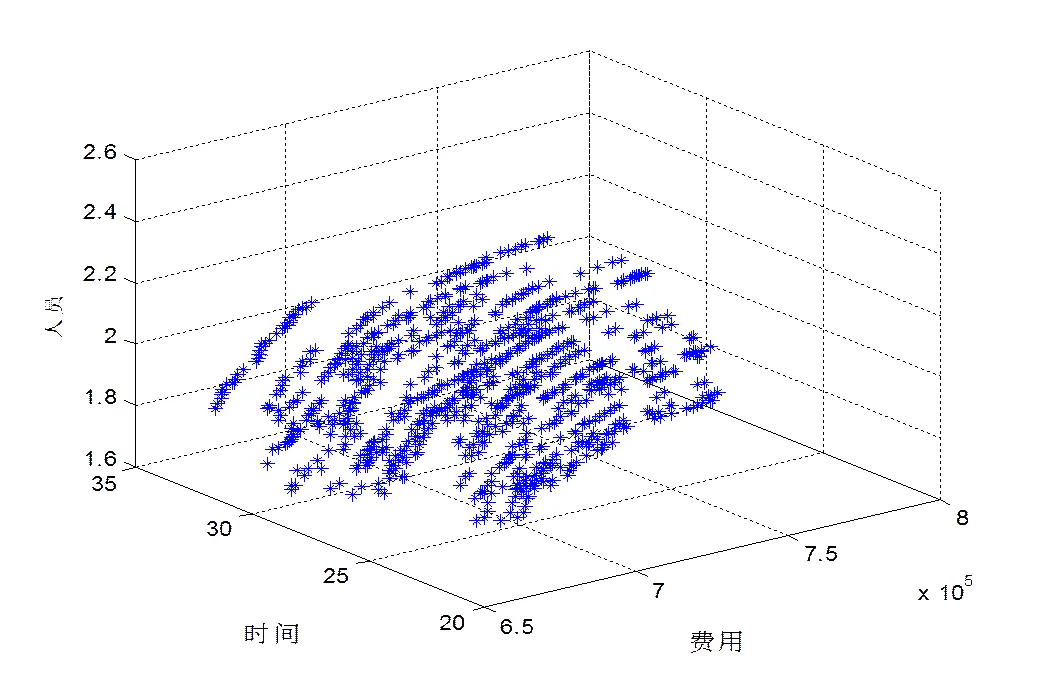
图2 实例问题的Pareto前沿

（1）表5给出了相对贴近度值最高的前10个方案。可以看出方案1相对接近度为0.534657，为非劣解中最大值。因此，选取方案1为最优方案。最佳方案的技能增值、研发周期和研发成本的目标值分别为2.2657、29.58个月和734200元，其解见表6。

（2）由于目标技能增值的权重较大，从而所得最佳方案1中技能增值总和为2.2657，在所有非劣解集中属于较大值，接近非劣解集中最大技能增值2.2755。其中，员工17、20、21和23的第四种技能增幅较大，分别为0.149、0.101、0.149和0.164，增长后技能值分别达到0.95、0.9、0.95和0.96；员工15的第五种技能增幅为0.149，增长后技能值达到0.95。由于第四种技能和第五种技能对该研发项目来说为核心技能且企业现有人才技能还需进一步提升，因此该方案符合企业实际需求。此外，技能初始值为最高值1的员工都没有安排在最佳方案内，这有助于将参与项目研发并获取研发技能和经验的机会留给其他需要进一步提升的员工，被选定员工的技能增值都在0.05和0.164之间，从总的结果来看，该最佳方案满足企业进行人才梯队培养的要求，符合企业人才发展战略规划。由于学习曲线函数是一次导数函数单调递增，二次导数函数单调递减，也即说明如参与项目研发的时间一样，初始技能越低的员工技能增值越大，初始技能越高的员工技能增值越小。因此，如果目标之一技能增值分配的权重大，那么将有更多的初始技能较低的员工入选研发项目。企业可根据人才培养的实际需要，调节技能增值目标的权重分配，改变方案中研发人员的选择安排。

（3）由于成本目标权重最小，因此最佳方案的成本734200元在所有非劣解中并不算少，最少的成本可低至648081元，但其对应方案的技能增值仅仅为1.7，远小于最佳方案；而开发周期目标的权重为0.3，属于中等水平，因此开发总周期为29.58个月在所有方案中属于中等偏下水平，最小和最大时间分别为24.8个月和32.08个月。如果企业要求更短的研发周期和更低的研发成本，可通过调整目标 函数的权重获得不同的员工安排方案，进一步满足目标要求,然而新的方案则是以降低员工技能增值为代价来满足其它两个目标的进一步优化。

（4）最佳方案为非劣解中的相对满意解而非绝对最优解。由于初始种群是随机产生的，每一次运行算法求解所得出的非劣解集不完全相同，因此，最终所求的最佳方案并不是唯一不变的，可通过多次运行程序来得到多个解方案，再进一步决策选取最终的满意方案。

（5）算法的总运行时间为261.43秒。子项目数量、子项目之间关系、所需技能数、员工数及员工技能分布情况都对算法效率有一定影响。项目数量越低、项目之间关系越简单、员工数越少，算法效率越高。

表5 贴近度值最高的10个方案的相对贴近度值及目标值

表6 贴近度值最高的10个方案的员工排列

5 结论

新产品研发项目组合中，研发周期和成本对新产品成功研发和上市具有关键作用，而人才是产品研发的主体因素，人才梯队建设是研发企业的长期战略规划之一。因此，本文提出以技能增值作为新产品研发项目组合调度的主要目标，兼顾考虑研发周期和成本目标，建立多目标模型来求解人员调度方案，并且决策者还可通过控制权重系数来权衡各目标的相对重要性，在非劣解集中选择出最佳方案。此外，若对本文中模型进行简单修改，同样适用于单个项目以及多项目调度中，模型通用性较强。后续研究中可进一步考虑员工之间学习率的不同以及学习曲线的遗忘效应来建立模型，使模型更贴近实践。同时，仍需进一步改进NSGA-Ⅱ算法，并尝试采用其它高级智能算法，以提高多目标调度模型的求解效率。

[1] Cooper RG， Edgett SJ， Kleinschmidt EJ. Portfolio Management for New Product Development：Results of an Industry Practices Study [M].New York， Basic Books， 1998：1-5.

[2] Cooper RG， Edgett SJ， Kleinschmidt EJ. New Problems，New Solutions：Making Portfolio Management More Effective [J]. Research Technology Management， 2000， 43（2）： 18-33.

[3] Archer NP， Ghasemzadeh F. An integrated framework for project portfolio selection [J]. International Journal of Project Management， 1999， 17（4）： 207-216.

[4] Ghasemzadeh F， Archer NP. Project portfolio selection through decision support [J]. Decision Support System， 2000，29（1）： 73-88.

[5] Christer Carlsson， Robert Fullér， Markku Heikkilä， et al. A fuzzy approach to R&D project portfolio selection [J]. International Journal of Approximate Reasoning， 2007（44）： 93-105.

[6] 寿涌毅，姚伟建.信息不确定下项目组合选择问题的鲁棒优化[J].系统工程，2009，27（7）：90-95.

[7] Cai X，Li KN. A genetic algorithm for scheduling staff of mixed skills under multi-criteria [J]. European Journal of Operational Research， 2000（125）： 359-369.

[8] 付芳，周泓.多项目人力资源调度实证研究[J].管理工程学报，2011，25（3）：73-77.

[9] Wu MC， Sun SH. A project scheduling and staff assignment model considering learning effect [J]. The International Journal of Advanced Manufacturing Technology， 2006 (28)： 1190-1195.

[10] Walter JG， Stefan K， Peter R， et al. Multi-objective decision analysis for competence-oriented project portfolio selection [J]. European Journal of Operational Research， 2010(205)： 670-679.

[11] Wright TP. Factors affecting the cost of airplanes [J]. Journal of Aeronautical Science， 1936（3）： 122-128.

[12] Yelle LE. The learning curves：historical review and comprehensive survey [J]. Decision Science， 1979， 10(2)： 302-328.

[13] Deb K， Pratap A， Agarwal S， et al. A Fast and Elitist Multiobjective Genetic Algorithm：NSGA-Ⅱ [J]. IEEE Transactions on Evolutionary Computation， 2002， 6（2）：182-197.

[14] 史峰，王辉.MATLAB智能算法30个案例分析[M].北京：北京航空航天大学出版社，2011：89-101

A New Product R&D Project Portfolio Scheduling Model Considering Learning Effect

CHEN Rong1, 2, LIANG Chang-yong1, 3, YE Chun-sen4

（1. School of Management, Hefei University of Technology, Hefei, 230009, China; 2. School of Economics and Management, Hefei Normal University, Hefei, 230601, China; 3. Ministry of Education Engineering Research Center for Intelligent Decision-making & Information Systems Technologies, Hefei, 230009, China; 4. School of Business Administration, Anhui University, Hefei, 230601, China）

Portfolio management for product innovation has surfaced as one of the most important senior management functions as we move into the 21st century. There are two ways for a business to do right projects, and do projects right. The first way is about project selection. The second way is about how a business allocates its capital and people resources.

The current literature on portfolio management focuses on the problem of selecting a subset of projects, but has little considerations on scheduling projects and assigning staff. Although economic objectives (e.g., return of investment) are common in current literature, time and competence objectives have not been thoroughly examined. In new product portfolio management, product development cycle is an essential objective as it determines the speed of new products launched into the market. Competence is also an indispensable objective because promoting competence of research and development is paramount to business’s future and even the survival. Considering learning effect, this article develops a multi-objective optimization model about multi-skilled workforce. It assumes that an employee has a variety of skills and the level of employee’s skill will rise along with time for research and development activities.. The objective functions of the model are to maximize the improvement of skills, minimize development cycle and minimize total cost. The model also examines the relationships between subsets of projects by considering each employee’s levels of different skills as constraints.

The model contains three decision goals: increment of skills, development cycle and development cost. It’s a typical NP-hard problem with nonlinear restrictions. For the computational solution, we develop an improved Nondominated Sorting Genetic Algorithm Ⅱ (NSGA-Ⅱ) to search Pareto-optimal solutions, and then determine the best solution by using the ideal-point method to transform the multi-objective model into a single-objective model. The weights of objectives are ascertained based on the preference of decision makers. How to deal with constraints is a critical factor for problem solving. Some of these constraints are realized by programming individual codes and population initialization. The other constraints are satisfied through correction of infeasible solutions and penalty functions.

We have conducted empirical analysis of a distribution network of an electrical device company in Hefei city in Anhui province of China with regard to its new product portfolio scheduling and staff assigning problems. The empirical analysis model contains eight kinds of skills, ten subprojects and forty employees. In the case, a project needs several skills. An employee holds more than one skill which are mastered by several employees. Adopting the improved NSGA-Ⅱalgorithm, the company obtains the best solution in improving skills, time and cost.

In summary, this article proposes a model of new product R&D Portfolio scheduling and staff assigning, and develops a corresponding algorithm for solving the problem. The empirical results show our model accords with business practice and the improved algorithm is effective. Our research can help an enterprise improve its decision in solving new product ‘s R&D Portfolio scheduling and staff assigning problems.

project portfolio scheduling; multi-skilled workforce assigning; learning effect; multi-objective optimization; new product R&D

中文编辑：杜 健；英文编辑：Charlie C. Chen

F224.1；C935

A

1004-6062(2016)02-0101-07

10.13587/j.cnki.jieem.2016.02.012

2014-09-27

2015-03-04

国家自然科学基金重点资助项目（71331002）；国家自然科学基金面上资助项目（71271072）；高等学校博士点基金资助项目（20110111110006）；安徽省哲学社会科学基金资助项目（AHSKQ2014D14）

陈蓉（1984—），女，安徽无为人，合肥工业大学管理学院博士研究生，合肥师范学院经济与管理学院讲师，研究方向：项目组合管理、产品研发管理、人力资源管理。