震后应急物流系统中双目标开放式选址：路径问题模型与算法研究

王海军，杜丽敬，马士华



震后应急物流系统中双目标开放式选址：路径问题模型与算法研究

王海军，杜丽敬，马士华

（华中科技大学管理学院，湖北 武汉430074）

灾害发生后，应急物资调度是救援工作核心。应急配送中心选址以及车辆路径安排在应急物资调度中仍然有很大的挑战。本文以平均车辆运输时间最小化和系统总成本最小化为目标，建立了基于多车型、双目标的开放式选址-路径问题混合整数规划模型。采用基于非支配解排序的遗传算法求解，得出包括若干非支配解的Pareto最优解集，为决策者提供多样化选择。最后以“汶川”地震为实例进行研究，结果论证了该模型与算法的有效性以及在实践中的可行性。

应急物流；多目标优化；开放式选址-路径问题；基于非支配解排序的遗传算法

0 引言

近年来地震灾害发生越来越频繁，成为严重危害人类生命的自然灾害之一，如2008年汶川地震, 2010年1月海地地震、2010年2月智利地震与2011年4月日本大地震等。灾害发生后短期内对应急物资产生较大需求，将有限的资源及时、合理地分配到受灾点至关重要。其中，应急配送中心选址与车辆路线安排是应急物资调度决策的核心。一方面需要在合适地点建立一定数目与规模的应急配送中心，以存储、分拨和中转来自全国各地的救灾物资；另一方面需要派遣合适的车辆选择合理的路线以将应急物资从配送中心配送至灾区。两者又是高度相关的[1]，因此应急管理人员需要对应急物资调度集成优化管理。

在应急配送中心选址方面，刘春林等为满足单一受灾点对应急物资的需求，以“时间最短”、“出救点最少”为目标建立模型，并提出了应急配送中心选择问题的模糊规划方法[2,3]；Sheu以需求满足率最大和总成本最小为目标建立动态规划模型[4]，采用模糊聚类优化方法将受灾点进行优先级分类，将应急物资优先运送到优先级较高的受灾点。在应急车辆路线安排方面，Haghani以最小化系统总成本为目标，建立了多模式应急物资配送网络流问题模型[5]，采用基于拉格朗日松弛的方法将模型划分为车辆流和商品流两个子问题求解；Fiedrich以地震发生后前三天总死亡人数最小为目标，建立了考虑多车型的应急物资分配模型[6]，采用模拟退火与禁忌搜索相结合的方法求得问题的满意解；Özdamar以需求未满足率最小化为目标建立多商品动态混合整数规划模型[7]，松弛容量约束转化为车辆流与商品流两个子问题求解；Vitoriano 等最先建立了基于成本、时间、优先权以及可靠性因素的多目标优化模型，采用目标规划的方法求解，实现对车型选择以及车辆路线优化[8]；另外，魏航等给出了时变随机网络下有应急限制期限制的应急路径选择算法[9]。在应急配送中心选址与车辆路线安排集成优化管理方面，Yi W 等以服务延迟最小化为目标建立了集成的选址-配送模型[10]，并提出了基于网络流的车辆路线求解算法；曾敏刚等以系统总成本最小为单一目标建立选址-路径优化模型，并采用选址与路线安排分开的两阶段启发式算法来求解，最后以实例验证模型可行性[11]。

从国内外文献分析看出，现有应急物流方面文献中配送中心选址与车辆路线安排通常分开研究，或者将选址-路径问题分为选址和路线安排两个子问题求解，无法实现集成优化；模型以单一目标函数为主，鲜有同时考虑其他相关因素。本文主要研究震后受灾点多物资需求下允许拆分配送基于时间与成本最小化的配送中心选址与多车型车辆路线安排问题，定义为双目标开放式选址-路径问题(Open Location Routing Problem, OLRP)。地震发生后应急路网不断变化，当前配送中心或许已不适合使用，因此应急物流中车辆不再返回出发点，而是停留在其所服务的最后一个受灾点，等待下一个任务，即开放式车辆路径。开放式车辆路径问题在传统物流中有专门的研究[12,13]，应急物流选址路径问题中研究还比较少。地震发生后，短期内对应急物资产生大量需求。当一个车辆无法满足某受灾点应急物资的需求时，允许其他车辆再次为其配送物资，即拆分配送(Split Delivery)，在应急物资调度中使用拆分配送更符合实际[14]。

1 双目标OLRP模型

1.1 模型假设

(1) 候选配送中心与受灾点地理位置关系已知，且道路的可用情况可以通过探测技术实时获得。(2) 每个车辆允许同时装载不同物资，同样，不同物资允许由同一个车辆运输。(3) 仅考虑当前网络中车辆可以到达的受灾点，需要飞机、轮船等其他运输方式才能到达的受灾点不做考虑。

1.2 问题描述

应急物资调度双目标的OLRP中，应急物流网络表示为=(,)，如图1所示。其中包括两个子集：候选应急物资配送中心集合与受灾点集合，为可用链路集合。为各点之间距离矩阵()，满足三角不等式，即对任意有。=()为地震灾害发生后可用链路上最大可以行使的速度矩阵()，具体数值根据道路的受损程度进行估计。考虑不同类型车辆进行物资配送，v表示车辆的平均行使速度，c表示车辆的单位距离成本，L表示车辆的最大容积。需要配送的应急物资为帐篷和水，考虑受灾点一天的需求量。需要决策的问题是建立合适数量与位置的配送中心，在配送中心和车辆容量的限制下选择合适的车辆并优化相应的路线将应急物资从配送中心运输到各个受灾点。服务结束时车辆停留在其所服务的最后一个节点，等待下次任务的分配；当某受灾点处应急物资需求不能由单一车辆满足时，允许拆分配送。即如图1中，车辆1从候选配送中心0出发，依次为受灾点1、2提供应急物资，其中受灾点2为其所服务的最后一个受灾点，车辆1停留在受灾点2处，不返回配送中心0；若受灾点2仍然有尚未满足的应急物资需求，则允许其它车辆为其提供服务。

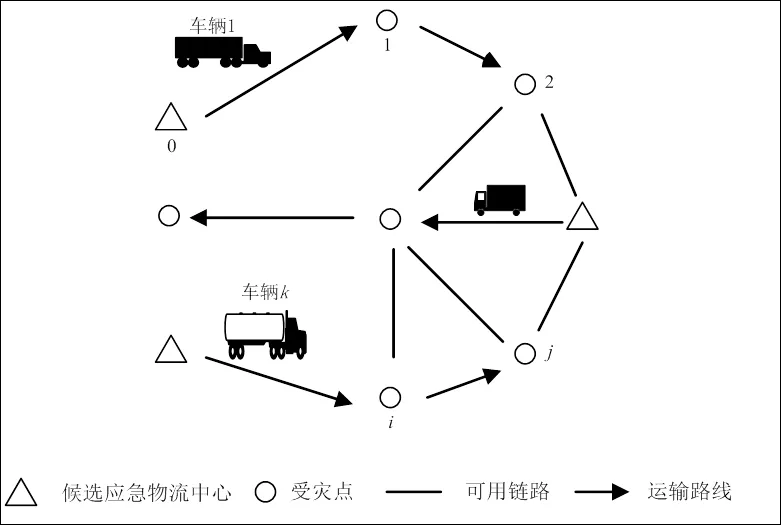
图1 应急物流系统中OLRP示意图

1.3 符号说明

模型中所用到的其他符号和变量定义如下：

其中决策变量为：

1.4 模型建立

应急物资优化调度的目标从两个方面来度量，其一时间上的有效性，以平均车辆路线运输时间最小化表示；其二是成本上的经济性，以最小化系统总成本表示。两个目标是相互冲突的，为最小化所有车辆平均路线运输时间，将建立相对较多的配送中心，增加了成本；要减少系统成本，一方面选择较少的配送中心，另一方面选择单位运输成本较低的车辆等，将导致车辆运输时间增加。

平均车辆路线运输时间最小化可使得应急物资尽可能快地配送给受灾人员，提高受灾人员存活率。在震后OLRP中，车辆停留在其所服务的最后一个受灾点，不返回配送中心，因此车辆在其服务路线上的运输时间为车辆从应急配送中心出发到达其所服务的最后一个受灾点的时间长度。

考虑到灾害发生初期应急资金的筹集不足，为最大程度地合理利用资金，系统成本最小化为另一个需要考虑的因素。震后OLRP系统中，总成本包括配送中心的建设费用和车辆运输费用两个方面。其中，应急配送中心的建设费用为；车辆运输费用为车辆从配送中心出发到达其所服务最后一个受灾点的运输费用，也即车辆在其服务路线所有链路上的行驶费用，表示为，则系统总运输费用为。设表示系统总成本，表示如下：

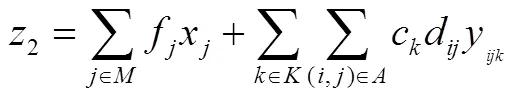
应急物流应急物资调度OLRP优化模型如下：

Min(3)

Min(4)

S.t.

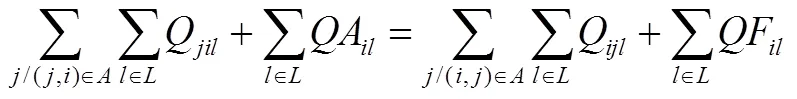
,(6)

(7)

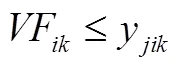
，(9)

(10)

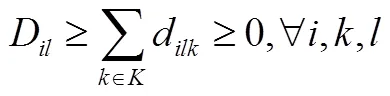
,，(12)

(13)

=0或1,,(15)

，，，(16)

目标函数(3)为平均车辆路线运输时间最小化，目标函数(4)表示系统总成本最小化。

约束(5)表示在受灾点与配送中心处应急物资流量均衡。约束(6)为在各点处车流量均衡。约束(7)表示配送结束后停留在各点的车辆数之和等于系统内最初可用车辆数。约束(8)表示路线上最后一个点必须由车辆提供服务。约束(9)表示服务结束时一个车辆可以且仅可以停留在一个节点上。约束(10)为车辆路线连续性约束。其一，车辆从配送中心出发，则最后不再返回；其二，除路线上最后一个受灾点外，车辆驶出点必为车辆驶入点；其三，在车辆停留在其所服务的最后一个节点，不再驶出。约束(11)要求配送到受灾点处应急物资的量不超过其需求量，且不能为负。约束(12)表示向受灾点配送所有应急物资总量不能超过系统内应急物资的可用量。约束(13)表示车辆所装载的应急物资量不能超过其容量。约束(14)-(15)为0-1整数变量约束。约束(16)为非负约束。

2 算法设计

求解多目标优化问题典型的方法是通过加权法、约束法与混合法等将多目标转化为单目标，再使用求解单目标的传统方法求解[8,15,16]。在这种方法下要取得不同权重下多个解，需要多次运行程序，并利用这些单目标问题最优解去近似Pareto最优解集。近年来，越来越多的研究者应用多目标进化算法求解多目标问题，如Pareto包络选择算法[17]，强度Pareto进化算法[18]，多目标分散搜索算法[19,20]等。2002年Deb提出了基于非支配解排序的遗传算法(Non-dominated Sorting Genetic Algorithm II，NSGA-II)，NSGA-II结合了非支配解排序机制、基于拥挤密度排序机制与遗传算法交叉变异操作算子，能够获得更好的Pareto最优解集[21]。由于LRP是NP-hard问题[22]，OLRP是LRP拓展，因此采用精确算法很难求解。本文采用NSGA-II求解，并采用多目标分散搜索 (Multi-objective Scatter Search, MOSS)算法进行比较。

2.1 多目标最优解概念

现实中许多问题需要同时优化几个目标，而且这些目标之间通常是相互冲突的。仅考虑一个目标值，不能判断所对应优化方案的优劣。因此在多目标优化中产生了Pareto最优解集概念。

2.2 NSGA-II设计

另外，文中采用的比较算法即MOSS算法也是以种群进化为基础的优化算法。种群初始化后选择高质量与多样化的个体进入参考集，通过组合与改进操作产生种群；对种群中个体进行非劣解与拥挤密度排序，选择参考集。相对NSGA-II而言，在选择机制上，其对参考集与中对应位置个体目标值比较，选择目标值占优的个体进入下一代参考集。

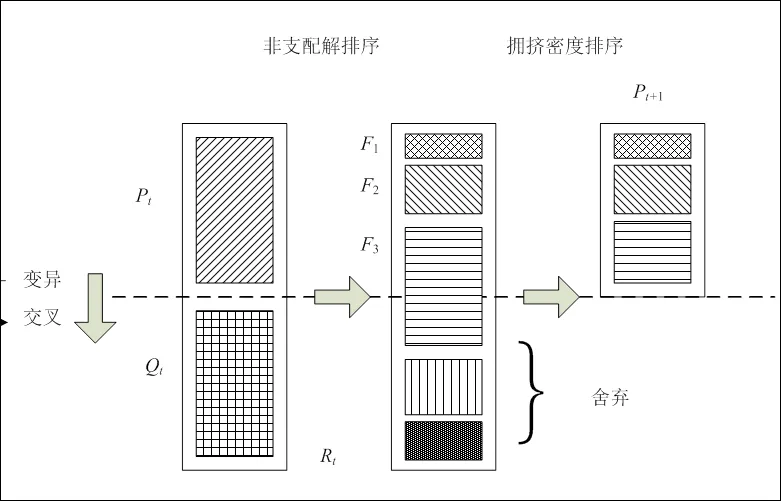
图2 NSGA-II 框架图

2.2.1染色体编码与初始化

本文中每个染色体有三个子串组成，且分别进行交叉和变异操作。令表示车辆总数，表示候选配送中心总数，表示受灾点个数，三个子串的产生方式如下：

子串1 =()；

子串2 =(1,, [1,])；

子串3 =()；

子串1为个车辆的随机排列；子串2有个基因位，每个基因位取值为1到的随机整数；子串3为个受灾点的随机排列。由此可见每个染色体长度为++。子串1中第一个基因位所代表车辆从子串2中第一个基因位所代表的配送中心出发，首先到达子串3第一个基因位代表的受灾点。若该受灾点的需求没有超过车辆容量，则继续配送下一基因位代表的受灾点；否则，该车辆停止在其所服务的最后一个受灾点。子串1中第二个基因位所代表的车辆从子串3中下一个基因位代表的受灾点开始提供救灾物资，以此类推。如果所有受灾点均有车辆提供服务，但车辆还有剩余且受灾点需求未全部满足，则从子串3的第一个基因位开始重复以上过程。这种方式下，为尽可能满足受灾点需求，一个受灾点可以被多个车辆服务，即拆分配送。

2.2.2变异、交叉操作与精英选择机制

图3 快速非支配解排序伪代码

为了增加解的多样性，提高Pareto最优解集质量，对染色体中三个子串分别进行变异与交叉操作。本文主要采用倒置变异、以及单点交叉与双点交叉相结合的交叉方式。NSGA-II最大的特点是其精英选择机制，一方面采用快速非支配解排序方法保留性能较好的解，使得算法加快收敛于Pareto最优解集；另一方面利用基于拥挤密度排序的方法确保解的多样性。

(1) 快速非支配解排序

本文中根据每个染色体所对应平均车辆运输时间和系统总成本两个目标函数值对种群中染色体进行排序，得出其所属于的Pareto前沿等级，称之为非支配解排序。前沿包含当前种群中所有Pareto最优解，前沿包含除去前沿到之后的所有非支配解。快速非支配排序具体参考文献[17]，其伪代码如图3所示。

(2) 拥挤密度排序

假设在解空间中，某个解与其周围最近的前个解的距离分别为，则该解的拥挤密度为。在本文中，即考虑当前种群中每个解对拥挤密度的影响，以避免由于分布不均匀而对拥挤密度做出错误判断。拥挤密度用来对属于同一Pareto前沿的解进行评价，保留拥挤密度较大的解可以提高算法的多样性。

2.3 NSGA-II步骤

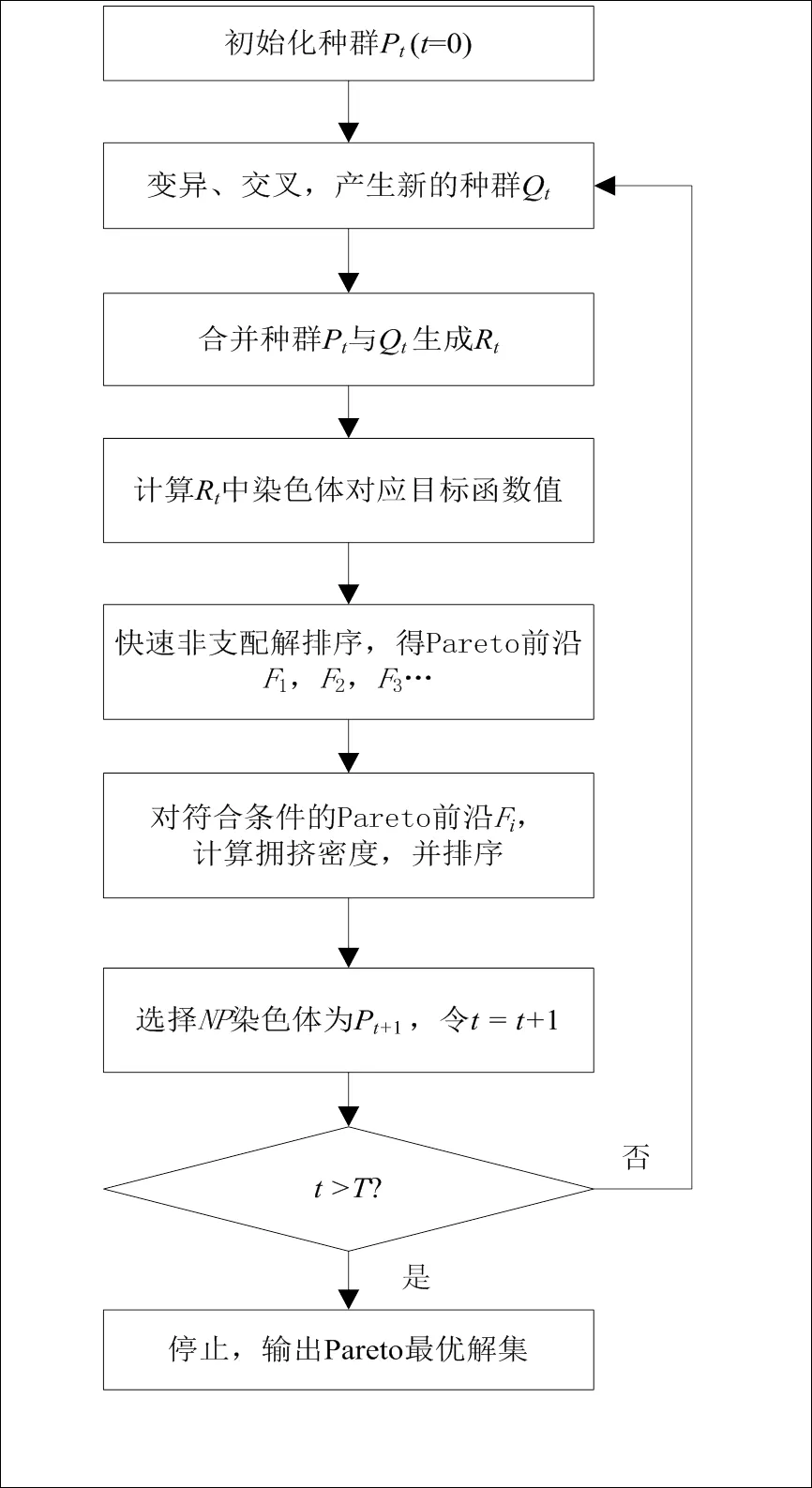
图4 NSGA-II流程图

本文中NSGA-II流程图如图4所示。具体步骤如下：

步骤4: 计算R中每个染色体所对应的目标函数值。

步骤5: 对R中所有染色体对应的目标函数值进行快速 非支配解排序，得出Pareto前沿等级。

步骤7: 根据Pareto前沿等级及拥挤密度，从R中选择个染色体组成p1，即为代染色体父体；

3 算例分析

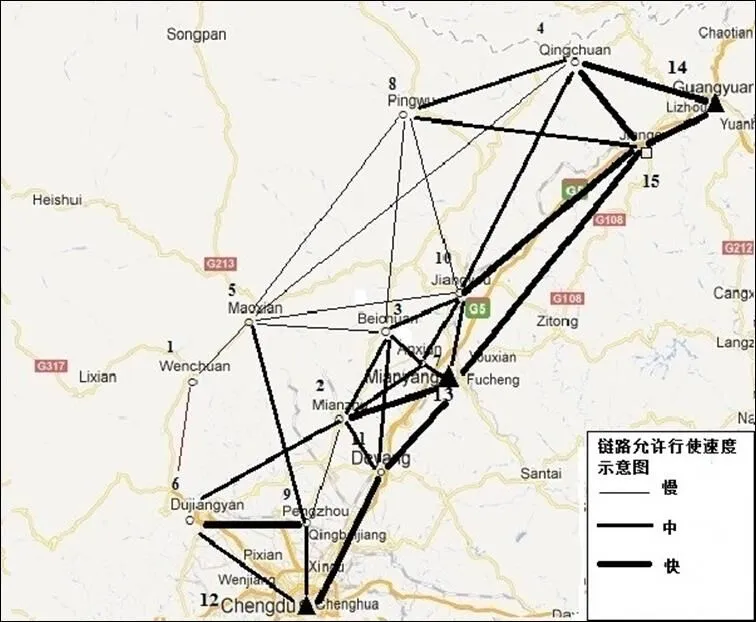
图5 受灾区域运输网络

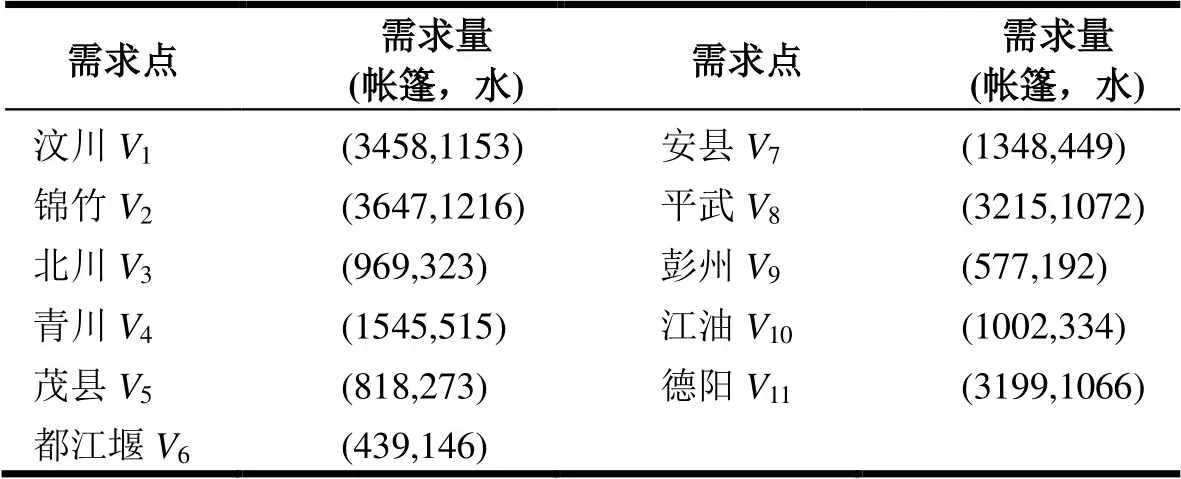
表1 受灾点应急物资需求量

表2 候选配送中心参数

表3 车辆参数

表4 应急物资参数

汶川地震造成至少6万人死亡，数千万人受伤，且公共设施如道路、桥梁等受到严重损害。本文主要研究地震后第一天受灾最为严重的11个区域。运输网络拓扑图如图5所示，其中受灾点为1到11，候选配送中心为12(成都)、13(绵阳)与14(广元)，另外15(剑阁)作为转运点，不考虑其需求。

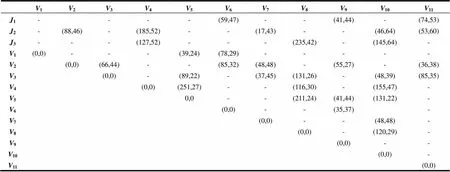
表5 运输网络参数

图中有34个可用链路，越粗则行使的最大允许速度越大。 需要配送的应急物资为帐篷和水，每个受灾点物资需求如表1所示；候选配送中心容量及固定建设费用见表2；所使用车辆中大型卡车有10辆, 另有6辆中型卡车与9辆小型卡车，具体参数见表3。表4为两种应急物资相关参数。

运输网络图的详细信息见表5，其中(，)表示所对应两点之间链路的距离(千米)及最大允许行使的速度(千米/时)，‘-’ 表示没有直接链路。前三行数据(1,2,3)表示3个候选配送中心与11个受灾点之间链路参数，其余表示11个受灾点之间链路参数。

3.1计算结果

本文采用Matlab®6.5对算法编程，所有的计算工作在同一台计算机上完成，表6为所使用计算机的性能参数。经过多次试验，NSGA-II控制参数设置为：种群规模=66, 变异概率p=0.1，交叉概率p=0.7。

对算法运行结果中不合理因素修正后，具体配送方案如图6与图7所示。其中，图6为基于目标1所得近似最优解解决方案，即最小化平均车辆路线行驶时间；图7为基于目标2所得近似最优解解决方案，即最小化系统运行总成本。受灾点处(，，)表示为其提供服务的三种类型(大、中、小)车辆数量。表7为两种配送方案下各目标值及受灾点需求满足率。

表6 计算机配置参数

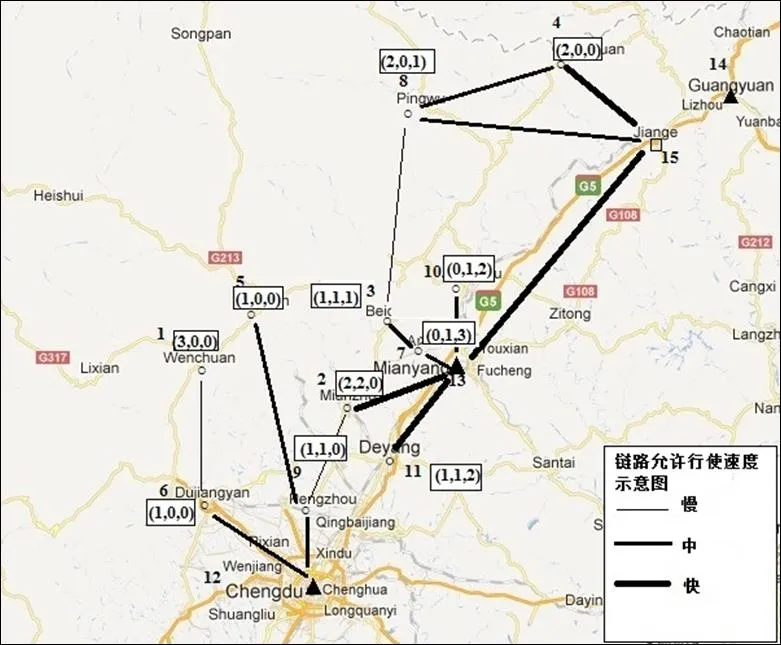
图6 最小化平均车辆路线行驶时间方案

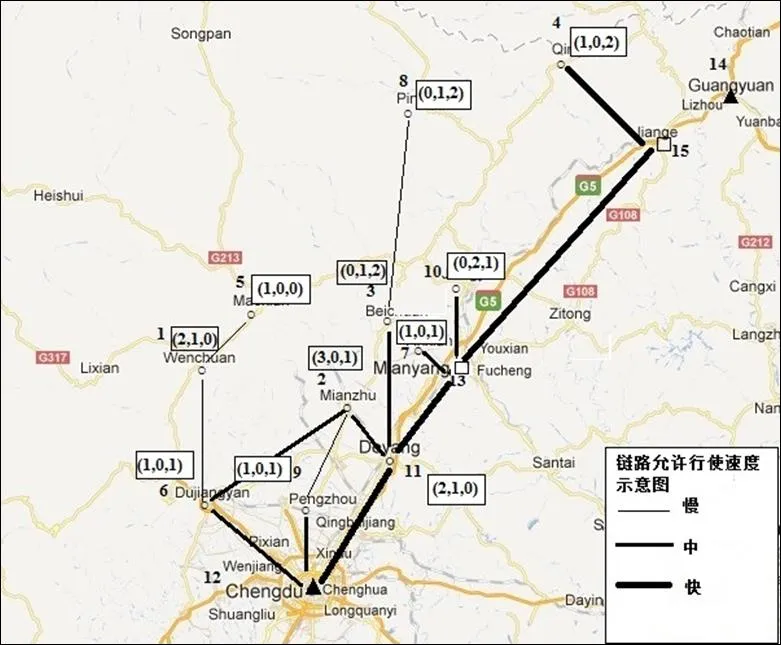
图7最小化系统总成本方案

在平均车辆行驶时间最小化方案中，候选配送中心12, 13开启，如图6所示。车辆最长路线运输时间为8.3小时，为某一小型车辆从配送中心出发经过点15为受灾点8配送应急物资。距离配送中心较远的受灾点(如点1，4，5，6等)较多采用大型车辆，一方面，大型车辆速度较快，用较快车辆配送较远距离可以缩短行驶时间；另外大型车辆容积较大，可以尽可能满足受灾点需求，减少配送次数。

为了最小化系统成本，图7中仅有候选配送中心12(成都)被选作配送中心，候选配送中心13作为转运点。从表7看出方案二的固定建设费用为10000元，方案一为25000元。小型车辆速度较慢，但是单位距离运输成本较低，因此使用小型车辆配送较远受灾点可以降低成本，如受灾点4(青川)、8(平武)。比较表10中两种方案下受灾点需求满足率可知：相对于方案一，方案二中距离配送中心较远的点需求满足率较小；反之，较大。

另外，比较图6与图7，图6所示方案选择了更多最大允许行驶速度较大的链路，如5-9，12-11，8-4，8-15；相对而言，图7选择1-5，即最大允许行驶速度较小的链路。

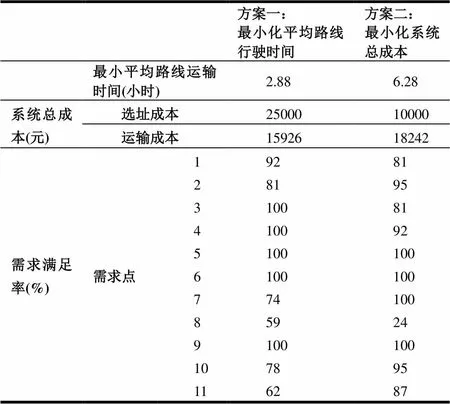
表7 两种目标下Pareto最优方案目标值

3.2算法比较

使用NSGA-II与多目标分散搜索算法(MOSS)两种方法对实例进行运算，得出的帕累托最优解集如图8所示。从图8中可以看出，NSGA-II对应解集中有17个解，MOSS算法对应解集有15个，且前者支配了后者。因此，决策者可以利用NSGA-II获得选择性更多、质量更高的方案。

图8 NSGA-II与MOSS算法所得非支配解集

表8 NSGA-II与MOSS所得最优目标值比较

表9 NSGA-II与MOSS运行时间

另外，本文实例在两种算法下所获得的时间与成本最优值如表8所示。NSGA-II中最小平均路线时间为2.88小时，相对于MOSS算法中3.53小时缩短了18.41%；前者系统总成本为28242元，相对于MOSS算法最小总成本减少了2961元。由此，NSGA-II可以获得时间上更快、经济上更为可行的应急物资调度方案。表9为两种算法分别运行15次之后平均运行时间。NSGA-II在一分钟之内运行结束，MOSS需要78秒，两种算法均在有效的时间内完成。

4 结论

地震一旦发生，短期内对应急物资产生大量需求，及时将应急物资供应到受灾区域是灾后救援工作的核心。灾后初期是救援工作的关键阶段，尽快地满足受灾人员需求能够最大可能地减少人员伤亡。由于初期物资短缺、时间有限，管理者需要对应急物资调度工作进行统筹规划、科学管理。一方面要选择合适的应急配送中心，存储、中转来自其他区域的救援物资；另一方面由于地震发生后道路、桥梁等基础设施部分遭到破坏，因此需要优化路网中救援车辆运输路线，以最小化物资配送时间和系统总成本。

本文研究了地震发生后不完全连通的路网下应急配送中心选址与车辆路径安排问题, 考虑了两种(帐篷和水)应急物资需求,以及三种类型运输车辆，在允许拆分配送的策略下建立了以平均车辆行驶时间和系统总成本为目标的开放式选址-路径问题数学模型。采用NSGA-II求解，得到包含多个支配解的Pareto解集，决策者可以根据实际情况和个人偏好选择合适的物资调度方案。最后以“汶川地震”作为算例，验证了模型的合理性与算法有效性，对灾害后应急物资调度有较大的实用价值。考虑灾后应急物流网络内各因素的随机性与动态性，下一步将进行基于时空网络的多周期选址-路径问题研究。

[1] Ballou RH, Masters JM. Commercial software for locating warehoused and other facilities [J]. Journal of business logistics, 1993, 14(2): 70-107.

[2] 刘春林，何建敏，盛昭瀚.应急系统多出救点选择问题的模糊规划方法[J].管理工程学报，1999，13(4): 23-24.

[3] 刘春林，施建军，李春雨.模糊应急系统组合优化方案选择问题的研究[J].管理工程学报，2002，16(2): 25-28.

[4] Sheu JB. An emergency logistics distribution approach for quick response to urgent relief demand in disasters [J]. Transportation Research Part E: Logistics and Transportation Review, 2007, 43: 687-709.

[5] Haghani A, Oh SC. Formulation and solution of a multi-commodity multi-modal network flow model for disaster relief operation [J]. Transportation research part A: Policy and Practice, 1996, 30(3): 231-250.

[6] Fiedrich F, Gehbauer F, Rickers U. Optimized resource allocation for emergency response after earthquake disasters [J]. Safety Science, 2000, 35: 41-57.

[7] Özdamar L, Ekinci E, Küçükyazici B. Emergency logistics planning in natural disasters [J]. Annals of operations research, 2004, 129(14): 217-245.

[8] Vitoriano B, Ortuño M. T, Tirado G,. A multi-criteria optimization model for humanitarian aid distribution [J]. Journal of Global Optimization, 2011, 51(2): 189-208.

[9] 魏航，刘璇.时变随机网络下基于成功和风险的应急路径选择研究[J].管理工程学报，2010，24(2)：68-74．

[10] Yia W, Özdamar L. A dynamic logistics coordination model for evacuation and support in disaster response activities [J]. European Journal of Operational Research, 2007, 179( 3): 1177-1193

[11] 曾敏刚，崔增收，余高辉.基于应急物流的减灾系统LRP研究[J].中国管理科学，2010，18(2)：75-80．

[12] Schrange L. Formulation and structure of more complex/realistic routing and scheduling problems [J]. Networks, 1981, 11(2): 229-232.

[13] Sariklis D, Powell S. A heuristic method for the open vehicle routing problem [J]. Journal of the Operation Research Society, 2000, 51(5): 564-573.

[14] Dror M, Trudeau P. Split Delivery Routing [J]. Naval Research Logistics, 1990, 37(3):383-402.

[15] Tzeng GH, Cheng HJ, Huang TD. Multi-objective optimal planning for designing relief delivery systems [J]. Transportation research part E, 2007, 43: 673-686.

[16] Chanta S, Mayorga ME, McLay LA. Improving emergency service in rural areas: a bi-objective covering location model for EMS systems [J]. Annual operation research, 2011, DOI 10.1007/s10479-011-0972-6.

[17] Corne DW, Knowles JD, Oates MJ. The Pareto envelope-based selection algorithm for multi-objective optimization.Parallel Problem Solving from Nature PPSN VI (Lecture Notes in Computer Science), 2000, 1917: 839-848.

[18] Paraskevi SG, Loannis AP, Chris TK,. Multi-objective evolutionary emergency response optimization for major accidents [J]. Journal of Hazardous Materials, 2010, 178: 792-803.

[19] Tavakkoli-Moghaddam R, Makui A, Mazloomi Z. A new integrated mathematical model for a bi-objective multi-depot location-routing problem solved by a multi-objective scatter search algorithm [J]. Journal of Manufacturing Systems, 2010, 29: 111-119.

[20] Antonio J. Nebro, Francisco Luna, Enrique Alba. New ideas in applying scatter search to multiobjective optimization [J]. Evolutionary Multi-Criterion Optimization, 2005, 3410: 443-458.

[21] Deb K., Pratab A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II [J]. IEEE Transactions on Evolutionary Computation, 2002, 6:182-197.

[22] 汪寿阳，赵秋红，夏国平.集成物流管理系统中定位-运输路线安排问题的研究[J].管理科学学报，2000, 3(2)：69-74．

Model and Algorithms for Integrated Open Location and Routing Problem in Emergency Logistics under Earthquake

WANG Hai-jun, DU Li-jing, MA Shi-hua

(School of Management, Huazhong University of Science and Technology, Wuhan 430074, China)

Earthquakes have already been major fatal disasters that threaten humankind’s life. Rescue efforts can reduce the impact of damage after an earthquake occurs. Distribution of relief goods is the focus of rescue work. Emergency managers need to find an optimal schedule for distributing relief to disaster areas with limited time and funds. The location of distribution centers and routes scheduling of vehicles are vital to the relief items distribution, which remains challenging in emergency logistics research and related fields.

In this paper we focus on the coordination of location of distribution centers (DCs) and vehicle routes scheduling for distributing relief items to disaster areas efficiently. The problem can be classified as an integrated open location-routing problem (OLRP) with bi-objective. In emergency logistics, with higher uncertainty and dynamic the former DC may not work in the next order in OLRP. Each dispatching vehicle stays at the last disaster areas it serves without returning to DC until the next mission is received. With large demand for relief items in disaster areas after earthquake, the capacity of vehicles may not be enough for fulfillment. Thus, disaster areas can be served more than once. This is called split delivery, which is a big feature from typical vehicle routing problem. It makes the research problem more realistic.

In the first part, we review literature on relief items distribution in emergency logistics. There is a lack of studies on the design of mathematical models and solution algorithms for OLRP in a post-disaster situation.

In the second part, we describe the bi-objective OLRP in emergency logistics. Sleeping bags and water are relief items mainly considered in this study. The relief items are considered for one day needed by disaster areas. Split deliveries are required once the demands of disaster area break the capacity of the serving vehicle. Two objectives are considered: (1) minimizing the average vehicle route time, and (2) minimizing the total cost, including the fixed establishing costs of DCs and the vehicle travelling cost. Objective (1) and (2) are conflict with each other. In the test instance section, we take this fact into account by considering the two objectives simultaneously. Mixed integer programming mathematic models of OLRP are presented.

In the third part, Non-dominated Sorting Genetic Algorithm (NSGA-II) is designed to solve the bi-objective model.Series of sets solutions called generations are computed by NSGA-II. Each generation consists of several individuals called chromosomes. Each chromosome denotes one strategy for relief distribution. Fast-Non-Dominated-Sort and Crowding-Density–Sort are used to select the elites into the offspring, which can guarantee the convergence and diversity of Pareto optimal solutions.

In the fourth part, ‘Wenchuan earthquake’ is conducted to illustrate the efficiency and potential advantages of the proposed method. The approximate optimal DC location and vehicles scheduling according to the above two objectives (minimize the average route travelling time and the total cost) are given. The results show that DC location and vehicle scheduling depend on each other. To minimize the average vehicle travelling time, more DCs are located, and vehicles with higher normal velocity are chosen. The higher normal velocity, the higher cost per kilometers the vehicles are. Thus, the total cost including the fixed location cost and vehicle travelling cost will increase. In contrary, to minimize the total cost fewer DCs are open and vehicles with lower cost per unit of travelling are scheduled. The solutions will support decision makers to direct the distribution of relief items under adverse conditions.

Comparisons are made between NSGA-II and Multi-Objective Scatter Search (MOSS) algorithm. The results have shown that the approximate Pareto optimal solutions obtained by NSGA-II dominate most of all the solutions obtained by MOSS, which verifies the strengths of the NSGA-II in solving multi-objective problems. This provides a profound basis to extend our method to more realistic assumptions.

Finally, it is expected that the proposed relief items distribution approach can improve the performance of emergency logistics managements. In the next step, multi-periods OLRP will be considered.

emergency logistics; multi-objective optimization; open location and routing problem; non-dominated sorting genetic algorithm

中文编辑：杜 健；英文编辑：Charlie C. Chen

F542

A

1004-6062(2016)02-0108-08

10.13587/j.cnki.jieem.2016.02.013

2013-04-08

2013-12-22

国家自然科学基金资助项目（70972020，71372135）

王海军(1970 — )，男，江苏如东人。华中科技大学管理学院副教授，博士生导师，研究方向：物流与供应链管理。