基于椭圆模型与改进NLCS的一站固定式大基线双站SAR成像算法
钟 华 胡 剑 张 松 孙闽红
基于椭圆模型与改进NLCS的一站固定式大基线双站SAR成像算法
钟 华*胡 剑 张 松 孙闽红
(杭州电子科技大学通信工程学院 杭州 310018)
在一站固定式双站SAR成像处理中,该文针对距离-方位2维空变描述不够准确导致成像性能迅速下降的问题,提出一种新的椭圆模型精确描述一站固定式大基线双站SAR的距离-方位空变特性,并基于此推导了改进的非线性调频变标(NLCS)成像算法。在距离向,首先利用相位去斜完成距离去走动和多普勒中心矫正,接着对剩余距离单元徙动和距离方位高次耦合项进行了去除处理。在方位向,根据一站固定式双站SAR的2维空变特性,提出了一种用于描述回波距离-方位空变特性的椭圆模型,基于该模型对空变的回波方位调频率进行了分析,并重新推导NLCS算法的方位变标函数和方位压缩系数。理论分析与仿真结果证明,所提出的模型不仅揭示了一站固定式大基线双站SAR数据的2维空变特性,而且对回波的距离-方位空变给出了更精确的解析式描述,使得基于该模型改进的NLCS算法可以获得更好的成像处理效果。
SAR成像;双站SAR;一站固定式; 非线性调频变标;椭圆模型
1 引言
双站合成孔径雷达(Bistatic Synthetic Aperture Radar, BiSAR)是将发射机与接收机分置于两个不同平台上的一种SAR模式。相对于传统单站SAR,双站SAR系统配置灵活多样,接收装置适装性强,电磁隐蔽性好,不仅能实现传统的侧视成像,还具备前视成像、长基线干涉、3维成像的能力,是新体制SAR技术的重要发展方向。一站固定式双站SAR(例如发射机固定)是双站SAR的一种特殊形式,该系统不仅容易构建与部署,而且可以完成区域监测、飞行器起降辅助等功能,在军民领域都具备广阔的应用前景。近年来,国内外进行了多次一站固定式双站SAR的实验,获得了较好的成像效果。
一站固定式双站SAR虽然相对容易部署,但其成像处理却异常困难。由于发射机与接收机之间相对位置随方位向时间变化,导致其回波具有2维空变特性[9],大基线、宽测绘带条件下这种空变尤为剧烈。因此,传统成像算法很难直接应用于一站固定式双站SAR的成像处理,必须对算法进行合理的创新性改进。
NLCS算法因其方位空变处理能力在双站SAR成像处理中得到了广泛的应用。该算法最初被用于处理方位空变的单站SAR数据[10],后来又被应用于天然具备2维空变特性的非平行轨迹双站SAR数据[11]。文献[12,13]在精心分析了大斜视非平行双站SAR回波2维空变特性的基础上,对该算法作了重要发展。文献[8,9,14]则基于双站SAR的2维空变特性和NLCS精巧的算法结构,提出了基于数值估计的NLCS算法。
虽然NLCS算法在一定程度上能处理双站SAR成像中的2维空变数据,但是由于这些算法没有对双站SAR距离-方位空变特性给出足够精确的描述,使得其成像处理能力受到了一定的限制。文献[11]直接采用了单站SAR的距离-方位模型对双站SAR进行逼近,导致该算法在处理大基线、宽测绘带双站SAR数据时成像性能有所下降。文献[12,13]分析了双站SAR的2维空变特性,并引入了距离偏移变量对双站距离-方位空变进行了建模,大幅提高了NLCS算法的成像性能,但该方法在一站固定式双站SAR成像处理中的适用性受到一定的限制。文献[8,9,14]采用数值法去逼近NLCS算法的方位向扰动函数,计算量较大。
本文对方位向NLCS算法进行了深入分析,并根据一站固定式双站SAR的回波特性,建立了一种新的双站距离-方位空变模型。该模型不仅揭示了双站SAR数据的2维空变特性,而且给出了更精确的解析式描述,为2维空变的双站SAR成像处理提供了新的思路。基于该模型本文为一站固定式双站SAR改进了NLCS算法的方位向扰动和方位向压缩函数。仿真结果表明,本文提出的改进的NLCS算法,在处理大基线、宽测绘带一站固定式双站SAR数据时具备更优良的成像处理性能。
2 信号模型

(2)

图1 一站固定式双站SAR几何构型
假设雷达发射线性调频信号,则点目标的接收回波解调之后可以表示为

(4)
3 距离向处理
接下来,进行线性距离项去除处理,以降低回波数据的距离-方位耦合,即在距离频域-方位时域去除线性走动分量,并同时矫正多普勒中心频率、移除距离调制项[12],其参考函数可以表示为
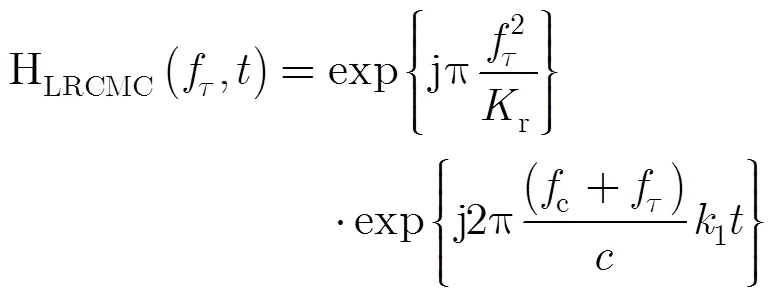
矫正过后的信号:
(6)
接下来,利用级数反演法(MSR)[15]将回波变换到2维频域。

其相位函数为
(8)
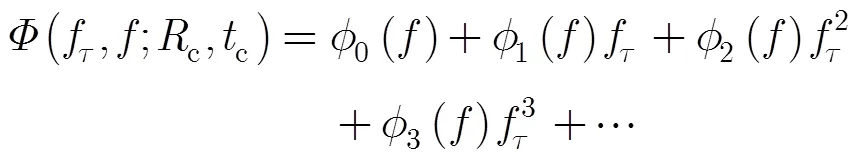
(10)
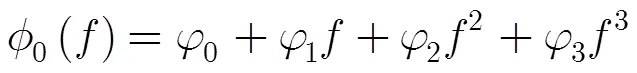
式(11)中,前两项系数分别表示常数相位和目标方位位置,第3项和第4项反映了目标方位调制信息,对成像至关重要。
接下来,将信号变换至距离时域-方位频域得到
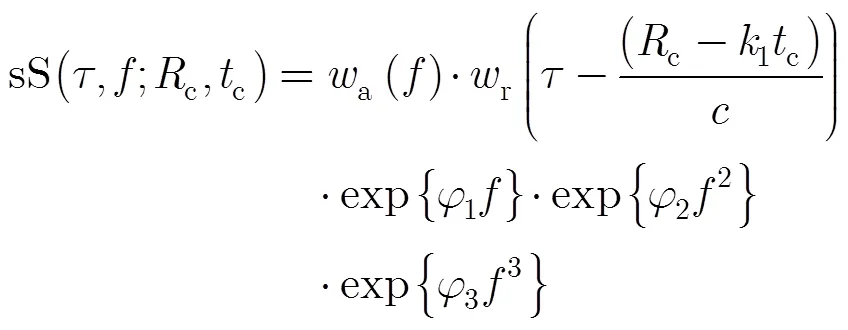
对双站距离表达式(2)取一阶泰勒展开有

此外,由式(12)可知,点目标方位向调制率为

4 方位向处理
在大基线方位时变双站SAR模式下,回波信号的距离-方位空变特性与单站SAR有着较大差异,而此前的研究对此缺乏足够的重视,导致成像算法的适用性受到了一定的制约。本节首先从一种新的角度对传统单站SAR方位向NLCS算法[10]进行解读,并依据单站SAR的距离方位空变关系建立了圆模型。在此基础上,依据双站SAR的距离方位空变特性建立起更为准确的椭圆模型。接下来,根据该模型推导出一种更为精确、有效的方位向NLCS算法用于一站固定式大基线双站SAR成像处理。最后,对方位向处理中所涉及的主要误差进行了分析,并给出了算法的边界条件和适用范围。
4.1 圆模型的引入
根据上一节的分析,若点目标和分别落在方位时间和处,其回波经距离向处理之后具有相同的,即点目标和的回波在距离向落入同一距离单元(见图2(b)),则可认为在模型空间中点目标和将处于以时刻的雷达位置为圆心,为半径的圆上,如图2(c)所示。由式(14)可知,此时点目标和回波的方位调制率与它们各自的波束中心斜距和相关,即具有不同波束中心斜距的点目标和具有不同的方位调制率。NLCS算法就是利用方位扰动函数,实现方位向调制率的均衡,而该算法成功的关键则是建立起点的斜距与参考点斜距的方位空变关系[10],即
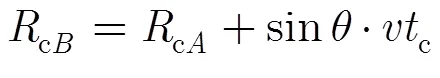
接下来,从几何模型的角度出发,论证上述距离-方位空变关系式,从而验证圆模型的合理性。从图2(c)可见,由圆的几何性质可知长为的半径与切线相垂直,因斜视角为固定值所以有与平行,作与平行,则有,点目标和相距不远时,点切线可近似看作与点相切,,因此有
(16)
由此可见,从圆模型推导出的结果式(16)与NLCS算法对进行距离方位建模的结果式(15)相一致。因此,单站NLCS算法,实际上是利用时刻雷达位置和参考点目标的位置作为两个支点,建立圆模型对周围区域进行方位空变的描述,从而实现了方位空变回波数据的成像聚焦处理。

图2 单站NLCS算法中,回波斜距、方位调频率与圆模型的关系
4.2 椭圆模型的建立
对于双站SAR而言,由于发射机与接收机的分离,圆模型显然已经不再适用,式(16)显然也无法准确描述波束中心斜距与方位时间的空变关系,必须建立起新的模型进行描述。受单站NLCS算法的分析结果启发,本文提出了适用于一站固定式大基线双站SAR的椭圆模型。
在一站固定式双站SAR中,若点目标和的回波经距离向处理之后,具有相同的,即和的回波在距离向落入同一个距离单元(见图3(b)),则可认为在模型空间中,点目标和将处于以时刻发射机和接收机的位置为焦点,点目标两焦点的距离和为长轴的椭圆上,如图3(c)所示,即,其中为点目标接收斜距进行线性距离徙动矫正之后的结果。

(18)
其中,

由式(18)可见,椭圆模型不仅能更为精确地描述双站SAR的距离方位空变关系,而且将2维距离-方向空变描述降至1维空变,为双站SAR的成像处理奠定了基础。若取,,,则有,这与单站中点目标和的斜距方位空变表达式(16)是相同的,即单站圆模型是双站椭圆模型离心率取0,半长轴取的特殊形式。而文献[11]在分析双站SAR的方位调频率时,实质上是直接采用了单站圆模型对双站椭圆模型进行的近似,在大基线、宽测绘带条件下存在较大误差。
图3 双站NLCS算法中,回波斜距、方位调频率与椭圆模型的关系
4.3 方位向均衡与压缩
结合上节分析的结论,把式(18)代入式(14)并作一阶展开,可得点的方位调频率。

接下来,本节将基于椭圆空变模型的方位向调频率的一阶展开式(20),对NLCS算法的变标函数进行重新推导,以得到适用于大基线、宽测绘带一站固定式双站SAR的成像算法。
首先,引入一个三次项的变标函数:
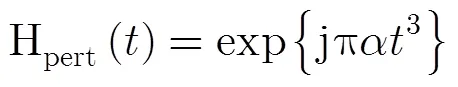
(22)
对于点目标则有

(24)
方位向均衡需去除方位调频率项所包含的位置信息,即令式(24)中第3项指数项为0,可得三次项变标系数:
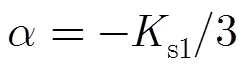
(26)
信号完成方位压缩返回2维时域即可得最终聚焦图像。
4.4 误差及边界条件分析
由前文分析可见,在本算法的方位向处理中涉及的误差主要包括两个部分。第1部分误差是式(18)对方位边缘点距离的一阶近似,其误差为

(28)
综合上述两部分误差,计算方位二次相位误差:

此处以一组一站固定式大基线双站SAR参数(表1)为例,对方位二次相位误差进行仿真计算,并与文献[11]和文献[12]的方法进行了对比,结果见图4。由分析结果可见,由于没有考虑双站SAR方位距离模型的特殊性,文献[11]的二次相位误差较大。文献[12]在文献[11]的基础上,对进行了距离偏移补偿,并对多普勒调频率进行了二次逼近,因此其二次相位误差小于文献[11]的结果。而本文方法对双站SAR的方位距离模型进行了合理建模,即便对多普勒调频率采用线性逼近,其二次相位误差依然优于文献[11]和文献[12]的结果。
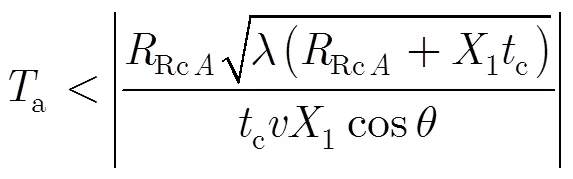
(31)
其中,

由边界条件的计算结果可见,合成孔径时间和目标方位向位置互为约束条件,在进行成像处理时,可使用式(30)和式(31)考察分辨率和成像幅宽等参数设计的合理性。
图4 方位二次相位误差结果分析图
5 仿真结果
为了验证算法的有效性,本文以表1所示的大基线构型一站固定式双站SAR为例,进行了数字仿真实验。发射机、接收机以及成像区域之间的几何关系如图1所示,收发斜距分别为38.45 km和11.55 km,发射机与接收机之间的基线长达30.0 km。目标区域由“5×9”点目标阵列组成,其场景大小为2.0 km×2.4 km,其中点目标距离向间隔为500 m,方位向间隔为300 m,其理论分辨率为3.0 m×3.0 m。
经改进的NLCS算法处理之后,整个测绘带区域的成像结果如图5所示。由成像结果可见,整个测绘带区域都得到了较好的聚焦效果。其中0点为中心点,在进行方位向处理时该点被选为参考点,1和2则为距离向和方位向的边缘点。
为了验证算法的聚焦性能,将文献[11]及文献[12]的双站NLCS算法的成像结果,与本文改进的双站NLCS算法的处理结果进行了对比。图6给出了方位向边缘点2的聚焦效果。由边缘点2的成像结果可见,由于文献[11]没有考虑双站SAR方位-距离的特殊性,导致边缘点2的方位向调频率存在较大误差,因此其点目标图像呈现明显的散焦状态,这是由于其对应的二次相位误差(见图4)造成的。文献[12]虽然对双站SAR的方位-距离模型进行了改进,但在边缘点的二次相位误差依然超过了,所以其聚焦效果存在拖尾和散焦现象。本文改进的NLCS算法则取得了更好的成像性能,边缘点2对应的二次相位误差,点目标聚焦性能较为理想,分辨率也接近理论值。
表2给出了本文算法处理结果的点目标方位向聚焦性能参数。尽管边缘点相对中心点聚焦性能有所下降,但与理论值相差不大。

图5 点目标阵列成像结果
6 结束语
本文针对一站固定式双站SAR方位向空变问题展开了研究,通过引入椭圆模型的几何关系,对一站固定双站SAR信号方位空变性进行了推导,给出了解析表达式,并在此基础上改进了NLCS算法的方位扰动和方位压缩处理。理论分析和仿真结果表明,与传统NLCS算法相比,本文改进的NLCS算法可以获得更好的成像效果。此外,本文所提出的椭圆模型及成像处理方法不仅可应用于一站固定式双站SAR的成像处理,同时也为大斜视、宽测绘带方位空变(非平行轨迹、非等速飞行等)的双站SAR、双站前视SAR的成像算法研究提供了新的思路。
表1 仿真参数表

仿真参数发射机接收机参数值 平台速度-200.00 m/s信号带宽50 MHz 斜视角-50.00°载波频率10 GHz 俯仰角82.44°45.00°多普勒中心频率5107 Hz 平台高度4.60 km2.10 km脉冲重复频率293.33 Hz 中心斜距38.45 km11.55 km合成孔径时间1.397 s
表2 本文算法成像性能参数

成像性能理论值点目标P0点目标P1点目标P2 峰值旁瓣比(dB)积分旁瓣比(dB)-13.3-13.29-13.24-13.18 -10-9.99-9.99-9.92
参考文献
[1] 杨建宇. 双基地合成孔径雷达技术[J]. 电子科技大学学报, 2016, 45(4): 482-501. doi: 10.3969/J.issn.1001-0548.2016.04. 001.
YANG J Y. Bistatic synthetic aperture radar technology[J]., 2016, 45(4): 482-501. doi: 10.3969/J.issn.1001-0548. 2016.04.001.
[2] 曾涛. 双基地合成孔径雷达发展现状与趋势分析[J]. 雷达学报, 2012, 1(4): 329-341. doi: 10.3724/SP.J.1300.2012.20093.
ZENG T.Bistatic SAR: State of the art and development trend[J]., 2012, 1(4): 329-341. doi: 10. 3724/SP.J.1300.2012.20093.
[3] 孟自强, 李亚超, 邢孟道, 等. 基于斜视等效的弹载双基前视SAR相位空变校正方法[J]. 电子与信息学报, 2016, 38(3): 613-621. doi: 10.11999/JEIT150782.
MENG Ziqiang, LI Yachao, XING Mengdao,Phase space-variance correction method for missile-borne bistatic forward-looking SAR based on equivalent range equation[J].&, 2016, 38(3): 613-621. doi: 10.11999/JEIT150782.
[4] LI Z Y, WU J J, HUANG Y L,Ground-moving target imaging and velocity estimation based on mismatched compression for bistatic forward-looking SAR[J]., 2016, 54(6): 3277-3291. doi: 10.1109/TGRS.2016.2514494.
[5] CHEN S, YUAN Y, ZHANG S N,. A new imaging algorithm for forward-looking missile-borne bistatic SAR[J]., 2016, 9(4): 1543-1552. doi: 10.1109/JSTARS.2015.2507260.
[6] ZHANG H, DENG Y K, WANG R,. Spaceborne/ stationary bistatic SAR imaging with TerraSAR-X as an illuminator in staring-spotlight mode[J]., 2016, 54(9): 5203-5216. doi: 10.1109/TGRS.2016.2558294.
[7] WANG R, WANG W, SHAO Y F,. First bistatic demonstration of digital beamforming in elevation with TerraSAR-X as an illuminator[J]., 2016, 54(2): 842-849. doi: 10.1109/TGRS.2015.2467176.
[8] ZENG T, HU C, WU L X,. Extended NLCS algorithm of BiSAR systems with a squinted transmitter and a fixed receiver: Theory and experimental confirmation[J]., 2013, 51(10): 5019-5030. doi: 10.1109/TGRS.2013.2276048.
[9] QIU X L, HU D H, and DING C B. An improved NLCS algorithm with capability analysis for one-stationary BiSAR [J]., 2008, 46(10): 3179-3186. doi: 10.1109/TGRS.2008.921569.
[10] WONG F H and YEO T S. New applications of nonlinear chirp scaling in SAR data processing[J]., 2001, 39(5): 946-953. doi: 10.1109/36.921412.
[11] WONG F H, CUMMING I G, and NEO Y L. Focusing bistatic SAR data using the nonlinear chirp scaling algorithm[J]., 2008, 46(9): 2493-2505. doi: 10.1109/TGRS.2008. 917599.
[12] LI D, LIAO G S, WANG W,Extended azimuth nonlinear chirp scaling algorithm for bistatic SAR processing in high-resolution highly squinted mode[J]., 2014, 11(6): 1134-1138. doi: 10.1109/LGRS.2013.2288292.
[13] WANG W, LIAO G S, LI D,Focus improvement of squint bistatic SAR data using azimuth nonlinear chirp scaling[J]., 2014, 11(1): 229-233. doi: 10.1109/LGRS.2013.2254106.
[14] LIZ Y, WU J J, YI Q Y,Bistatic forward-looking SAR ground moving target detection and imaging[J]., 2015, 51(2): 1000-1016. doi: 10.1109/TAES.2014.130539.
[15] NEO Y L, WONG F H, and CUMMING I G. A two- dimensional spectrum for bistatic SAR processing using series reversion[J]., 2007, 4(1): 93-96. doi: 10.1109/LGRS.2006.885862.
钟 华: 男,1978年生,讲师,研究方向为信号与信息处理.
胡 剑: 男,1991年生,硕士生,研究方向为信号与信息处理.
张 松: 男,1990年生,硕士生,研究方向为信号与信息处理.
孙闽红: 男,1974年生,副教授,研究方向为信号与信息处理.
Improved NLCS Algorithm Based on Ellipse Model for One-stationary Bistatic SAR with Large Baseline
ZHONG Hua HU Jian ZHANG Song SUN Minhong
(,,310018,)
In One-Stationary Bistatic Synthetic Aperture Radar (OS-BiSAR) imaging, imprecise description of 2-D range-azimuth space-variant property usually leads to deterioration of final SAR image rapidly. In order to solve this issue, a new ellipse model is proposed to precisely describe range-azimuth space-variant property of OS-BiSAR with large baseline, and an improved Non-Linear Chirp Scaling (NLCS) algorithm is also derived based on this model. First, a phase de-ramp operation is performed to remove the linear Range Cell Migration (RCM) and Doppler centroid in range frequency domain. Then, the residual RCM and high order range-azimuth coupling terms are removed. Thirdly, a new ellipse model is established to describe range-azimuth space-variant property of OS-BiSAR, and then the azimuth frequency modulation rate of space-variant echo is analyzed. Moreover, azimuth scaling function of NLCS and azimuth compression factors are re-derived. Theoretical analysis and simulation results show that the proposed model not only reveals the property of 2-D azimuth-variant in OS-BiSAR, but also provides a precise analytical expression to depict the 2-D range-azimuth space-variant property of OS-BiSAR. Furthermore, simulation results validate that the improved NLCS algorithm based on this new model has high imaging performance.
SAR imaging; Bistatic SAR; One-stationary; Non-Linear Chirp Scaling (NLCS); Ellipse model
TN957.52
A
1009-5896(2016)12-3174-08
10.11999/JEIT161016
2016-09-30;改回日期:2016-11-25;
2016-12-14
钟华 hzhong@hdu.edu.cn
国家自然科学基金(61301248, 61271214),中国航天科技创新基金
The National Natural Science Foundation of China (61301248, 61271214), Chinese Innovation Foundation of Aerospace Science and Technology
——2022 F1意大利大奖赛

