一种在线计算多模式空间矢量调制算法及其FPGA实现

吴瑕杰 宋文胜 冯晓云,2



一种在线计算多模式空间矢量调制算法及其FPGA实现

吴瑕杰1宋文胜1冯晓云1,2

（1. 西南交通大学电气工程学院 成都 610031 2. 西南交通大学牵引动力国家重点实验室 成都 610031）

针对大功率牵引传动系统中开关频率低的特点，在列车运行全速度范围内，牵引逆变器广泛采用多模式调制算法。为此，给出了一种新颖的在线计算多模式空间矢量脉宽调制（SVPWM）算法并研究了不同调制模式间的切换方法。给出了该算法基于现场可编程逻辑门阵列（FPGA）的详细设计方案，通过简化乘法器、高效率开方器、除法器等关键性设计使核心数字信号处理器（DSP）避免了大量运算，同时兼具FPGA速度快、可靠度高、可移植性好等优点。最后，采用DSP-FPGA的控制系统，基于RT-LAB的半实物（HIL）实验平台对该在线计算多模式SVPWM算法的正确性和基于FPGA设计方案的可行性进行了验证。

空间矢量脉宽调制 在线 多模式 现场可编程逻辑阵列

0 引言

我国高速动车组牵引传动系统主要分为两电平牵引变流器驱动系统和三电平二极管中性点钳位（Neutral Point Clamped, NPC）变流器驱动系统两类[1]。目前，逆变器调制算法主要分为载波调制（SPWM）与空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）两类。相比于SPWM技术，SVPWM技术以其易于数字化实现、电压利用率高等优点，广泛应用于两电平牵引逆变器的调制[1-6]。

大功率交流牵引传动系统启动时，由于载波比较大，由异步SVPWM造成的逆变器输出电流正负半周对称性较好，因此，系统实现简单且具有良好的控制性能。但随着逆变器输出频率逐渐升高，在一个调制周期内脉冲数将逐渐减少，由异步SVPWM造成的逆变器输出电流正负半周不对称情况严重，导致逆变器输出电流容易产生畸变，引发较大的转矩脉动，难以保证系统具有良好的控制性能[7]。目前，为了保证波形的对称性与较好的谐波性，通常采用特定谐波消除技术比如SHEPWM[8-12]，但该技术需要事先根据优化目标离线计算得出开关角，在优化开关角度计算上的复杂性限制了其在某些领域的使用。此外，该方法只适用于稳态条件，在动态过程中开关角度易产生混乱，从而引起电流谐波剧增，甚至导致调制算法失败[7]。以S. R. Bowes为代表的一些学者在此基础上提出了一些实时计算方法用以近似实现SHEPWM[13-16]，但仍存在一些使用限制，并且计算精度难以得到保证。因此，为了弥补异步SVPWM在低载波比时调制性能的不足以及SHEPWM算法灵活性的不足，有必要采用一种可以实时计算且适用于低载波比情况的调制算法。文献[17]论述了一种基于DSP实现的多模式SVPWM调制算法，但并未对多模式SVPWM算法进行详细的理论分析和设计方案；作为顺序处理器，DSP按照顺序逐条执行指令会导致时间延迟与性能下降。此类算法多以离线方式实现，且由于DSP IO数目的限制不利于向多电平拓扑延伸。随着FPGA技术的不断成熟，利用FPGA完成SVPWM相关工作，不仅兼具硬件电路速度快、可靠性高、设计复用性好等优点[18,19]，同时能将核心控制器DSP从繁重的重复性计算中解放出来，使其重点运行核心控制程序[20,21]。

本文以两电平牵引逆变器的调制算法为研究对象，首先给出了一种将低速异步SVPWM与中高速分段同步SVPWM相结合的在线计算多模式SVPWM算法。该方法将同步调制频段分为九脉冲、七脉冲、五脉冲、三脉冲四种调制模式，同时为了进一步减小转矩脉动，改善切换性能，将七脉冲、五脉冲分别设计为七脉冲A和七脉冲B、五脉冲A和五脉冲B的组合形式。其次详细介绍了该在线计算多模式SVPWM算法基于FPGA的设计方案以及不同调制方式间的切换方法。最后基于DSP-FPGA的控制系统和RT-LAB半实物实验平台进行了实验验证。

1 异步SVPWM算法原理

基于两电平牵引逆变器主电路拓扑结构，定义其三相桥臂状态函数为

式中，S为逆变器A、B、C三相桥臂状态函数； 1为上桥臂导通；0为下桥臂导通。

本文将整个空间分为6个扇区（Ⅰ～Ⅳ），以第Ⅰ扇区为例，对两电平异步SVPWM算法进行简要的阐述。

（a）扇区分割

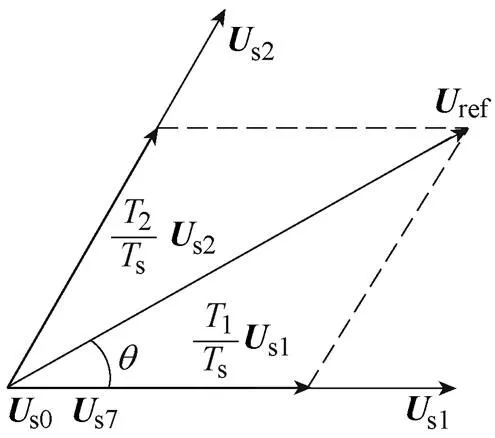
（b）矢量合成

图1 异步调制矢量合成图

Fig.1 Component of space vector for asynchronous modulation

定义调制度为

式中，dc为直流侧电压矢量；ref为参考空间电压矢量。

参考空间电压矢量ref由空间电压矢量s1和s2合成，在一个开关周期s内，由伏秒平衡原理可得

式中，1、2为基本空间电压矢量s1和s2的作用时间；0、7为零矢量s0和s7的作用时间；s为开关周期。

解得基本空间电压矢量s1和s2作用时间为

将零矢量总作用时间平均分配给s0和s7，则有

由前面计算得出的基本矢量作用时间并根据7段式PWM信号生成原理就可以得到一个开关周期内各相桥臂的开关序列模式，如图2所示。

图2 一个开关周内各相桥臂的开关序列模式

2 分段同步SVPWM算法原理

根据我国目前高速动车组的发展现状和高压大电流的电力电子器件发展水平，在电力牵引传动系统中，考虑到逆变器开关频率较低的实际应用情况，为了有效减小脉冲电压中的高次谐波含量，需要保证控制器输出脉冲具有三相对称性（3PS），半波对称性（HWS）和四分之一对称性（QWS）。本文将整个同步调制按照逆变器输出电压频率的不同分为九脉冲、七脉冲、五脉冲和三脉冲四种同步调制方式，同时，为了进一步改善不同同步SVPWM方式间的切换性能，将七脉冲与五脉冲进一步分别设计为A、B两种调制方式，本文以九脉冲、七脉冲A和七脉冲B为例进行详细分析。

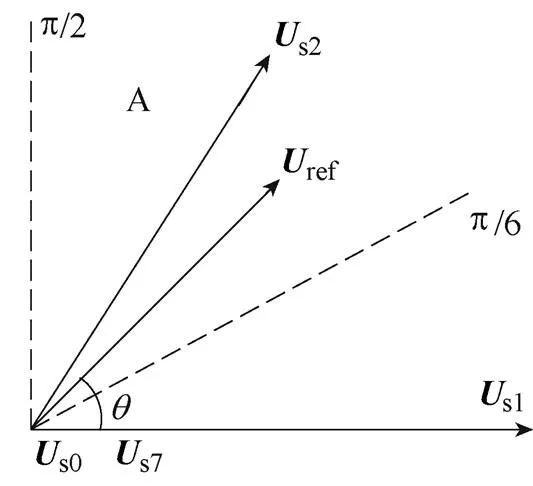
图3 九脉冲同步调制矢量合成

2.1 九脉冲与七脉冲A调制

以每两个基本空间电压矢量（s0～s7）夹角平分线为分界，将整个参考电压矢量空间均分为A～F六个区域，当参考空间电压矢量的位置角p/6＜＜p/2时，即参考空间电压矢量ref位于A区域时，参考空间电压矢量ref的作用效果可以用这一区间的主矢量s2及零矢量s7的作用效果进行等效替代。

根据数字控制的固有特点，假设参考空间电压矢量ref以角速度逆时针旋转，在一个开关周期s内，连续变化的参考空间电压矢量ref按照固定的时间间隔c被离散化为个独立的矢量，其中第个矢量为ref()，则根据伏秒平衡原理可得

式中，c为控制周期，即从控制器对传感器的反馈信号进行采集到计算出参考空间电压矢量ref()的时间；2为主矢量s2的作用时间。

将式（6）所示关系分解为垂直于主矢量s2和沿着主矢量s2两个方向，由于垂直于主矢量方向

因此，只需考虑沿着主矢量方向，存在关系

由式（8）化简可得

假设参考空间电压矢量ref的角速度0在每一个开关周期s内保持不变，即

将式（10）关系代入式（9）可得

解得主矢量s2和零矢量s7的作用角度为

式中，2为A区域内主矢量s2总作用角度；7为A区域内零矢量s7总作用角度。

为满足同步调制所需三个对称性条件，九脉冲同步调制采用等脉宽方式并按照固定的矢量作用序列产生PWM信号。表1给出了参考空间电压矢量位于A区域时九脉冲同步调制矢量作用序列及对应的作用角度区间。

表1 九脉冲同步调制作用角度分配（A区）

Tab.1 Angle distribution of nine-pulse synchronous modulation for region A

同理，对于七脉冲A同步调制，采用类似九脉冲同步调制的分析方法，考虑参考空间电压矢量ref位于A区域的情况，可以解得主矢量s2及零矢量s7的作用角2和7如式（12）所示，然后采用等脉宽方式生成PWM信号。表2给出了参考空间电压矢量位于A区域时七脉冲A同步调制矢量作用序列及对应的作用角度区间。

表2 七脉冲A同步调制作用角度分配（A区）

Tab.2 Angle distribution of seven-pulse A synchronous modulation for region A

2.2 七脉冲B调制

对于七脉冲B同步调制，同样考虑参考空间电压矢量ref位于A区域的情况，与九脉冲同步调制和七脉冲A同步调制不同，此时参考空间电压矢量ref的作用效果需要用一个主矢量s2、两个辅矢量s1和s3以及零矢量s7的作用效果进行等效替代。

首先，将整个A区域均分为A1、A2和A3三个小区域，如图4所示，为了实现相对于七脉冲A同步调制更加精细、准确的等效替代，当参考空间电压矢量ref分别位于三个小区域内时，需采用三种不同的矢量合成方式。表3给出了每个小区域对应的矢量作用序列。

图4 七脉冲B同步调制矢量合成

表3 七脉冲B同步调制矢量作用序列（A区）

Tab.3 Vector sequence of seven-pulse B synchronous modulation for different region in region A

然后，考虑当参考空间电压矢量ref位于A2小区域时，同理，只需考虑参考空间电压矢量沿着主矢量方向的作用，根据伏秒平衡可得

式中，s2为A2区域内主矢量；2(2)为A2区域内主矢量s2作用时间。

由此可以化简参考空间电压矢量ref与主矢量s2的对应伏秒关系为

解得主矢量s2及零矢量s7在A2小区域内作用角度为

式中，2(2)为A区域A2小区域内主矢量s2作用时间；7(2)为A区域A2小区域内零矢量s7作用时间。

为了保证脉冲信号的四分之一对称性（QWS），A1与A3两个小区域需在A2小区域两侧对称分布。所以，A1和A3内零矢量作用角度均为7(2)/2。

根据主矢量s2与辅矢量s1和s3之间存在的等效替代关系，可以将整个A区域内参考空间电压矢量与主矢量、辅矢量间伏秒关系表示为

式中，2(13)为A区域A1和A3小区域内主矢量s2作用角度。

由于基本矢量模值|s1|=|s2|=|s3|，小区域A1与A3中主矢量与辅矢量作用角度可表示为

式中，13(13)为A1和A3区域内辅矢量s1和s3总作用角度。

采用等脉宽的方式，给出七脉冲B同步调制矢量作用序列及作用角度分配见表4。

表4 七脉冲B同步调制作用角度分配（A区）

Tab.4 Angle distribution of seven-pulse B synchronous modulation for region A

本文以九脉冲、七脉冲A和七脉冲B三种同步调制方式为例，考虑当参考空间电压矢量ref位于A区域的情况，对三种同步调制方式进行了详细的推导与分析。同理，可以得到五脉冲A、五脉冲B与三脉冲两种同步调制方式的矢量作用角度计算公式，并推广到A区域以外的其他几个区域。

3 不同调制模式的切换

不同调制方式间的切换是多模式SVPWM算法的一个关键问题。在不同的调制方式下，脉冲所表征的有效基波信息并不完全相同。当发生切换时，由于基波的幅值和相位会发生突变，导致输出电压、电流波形发生突变，转矩脉动及谐波突增，从而使电机使用寿命减少。在不同调制算法之间进行切换时，需要保证参考空间电压矢量的连续性，即切换前后参考空间电压矢量的幅值与相位不突变；另一方面，当逆变器输出电压频率恰好在切换频率点附近时，就会出现在两种不同调制方式间频繁切换的情况。同时切换点与切换时刻的选择也是不同调制方式间平滑切换的关键。为此，本文设计了一种不同调制方式间的切换方法，首先，为了充分利用开关频率，经过详细分析与仿真验证，表5给出了逆变器在不同输出频率段对应的调制方式。其次，为了保证切换前后参考空间电压矢量的连续性，切换时刻选择在前调制模式最后一个脉冲信号结束之后，后调制模式第一个脉冲信号开始之前。

表5 逆变器输出电压频率与调制方式关系

Tab.5 Relationship of voltage frequency and modulation

4 基于FPGA的实现方案

在本设计中，基于Xilinx公司FPGA芯片和VerilogHDL与Schematic的设计方式，设计了在线计算多模式SVPWM电路。图5给出了在线计算多模式SVPWM电路功能模块划分。

图5 在线计算多模式SVPWM电路模块组成

4.1 基于加法器/移位寄存器的乘法器设计

然后，根据展开的级数形式即可得出硬件电路设计方法。图6为乘法器的硬件电路描述。整个系统以16位的数据长度进行定点运算时，异步SVPWM方式的PWM模块分辨率不足13位，因此只需取到级数的第六项即可满足精度要求。

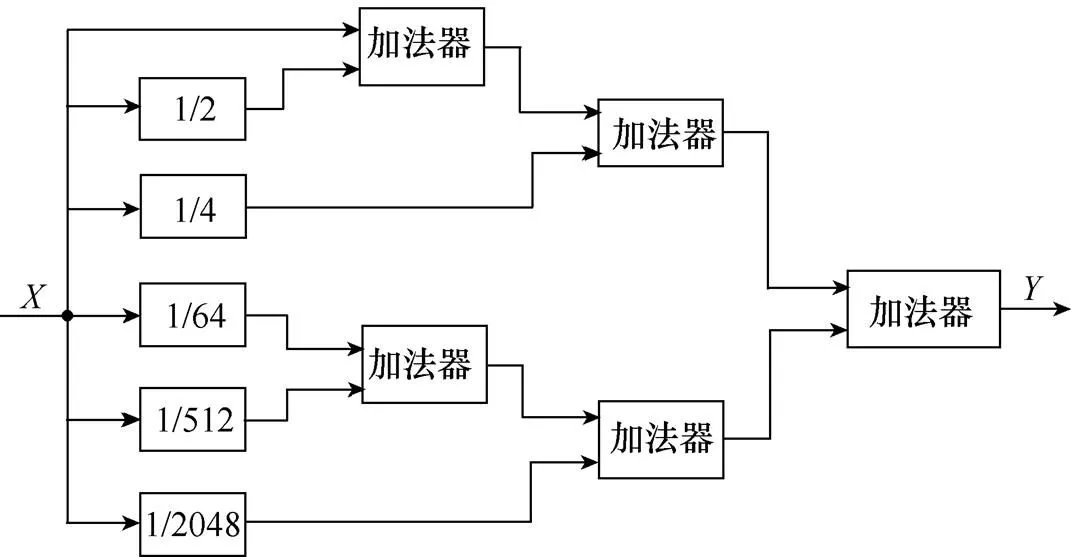
图6 乘法器电路描述

4.2 基于加法器/移位寄存器的开方器设计

本设计采用定点方式完成计算且在算法中存在大量除法运算。为达到高速、低资源占用的设计要求，图7给出了一种除法器的设计思路。整个除法运算主要包括如下步骤：①加载被除数、除数，同时将商和余数清零；②将左移1位并将移出的这一位赋给的最低位；③比较和，若≥，则将更新为-，同时将左移1位并将其最低位赋值为1，否则，保持不变，将左移1位并将其最低位赋值为0。如此循环，便可得到需要的商和余数。

图7 除法器算法描述

4.3 基于加法器/移位寄存器的开方器设计

本设计在同步调制部分需要进行开方运算。由于整个系统以16位的数据长度进行运算，为保证数据不会溢出以及输出16位的开方结果，本文给出了一种基于加法器和移位寄存器的简化开方器设计。

由于被开方数为32位，则开方结果为16位，余数为17位，共需进行16次迭代运算得到开方结果。图8给出了开方器的硬件结构。

图8 开方器硬件结构

5 实验研究

为了验证多模式空间矢量调制算法及基于FPGA设计方案的正确性与可行性以及算法的稳态与切换性能，对该算法进行了半实物实验研究，并给出了异步、九脉冲、七脉冲A与七脉冲B三种调制方式的稳态波形与各调制方式间切换的电流波形。图9给出了该半实物实验系统的实物图。该系统包括TMS320C6713 DSP+Xilinx Spartan 3E FPGA核心控制箱和RT-LAB半实物实验平台以及上位机三个部分。表6给出了半实物实验的相关参数。

图9 半实物实验系统实物

表6 半实物实验系统参数

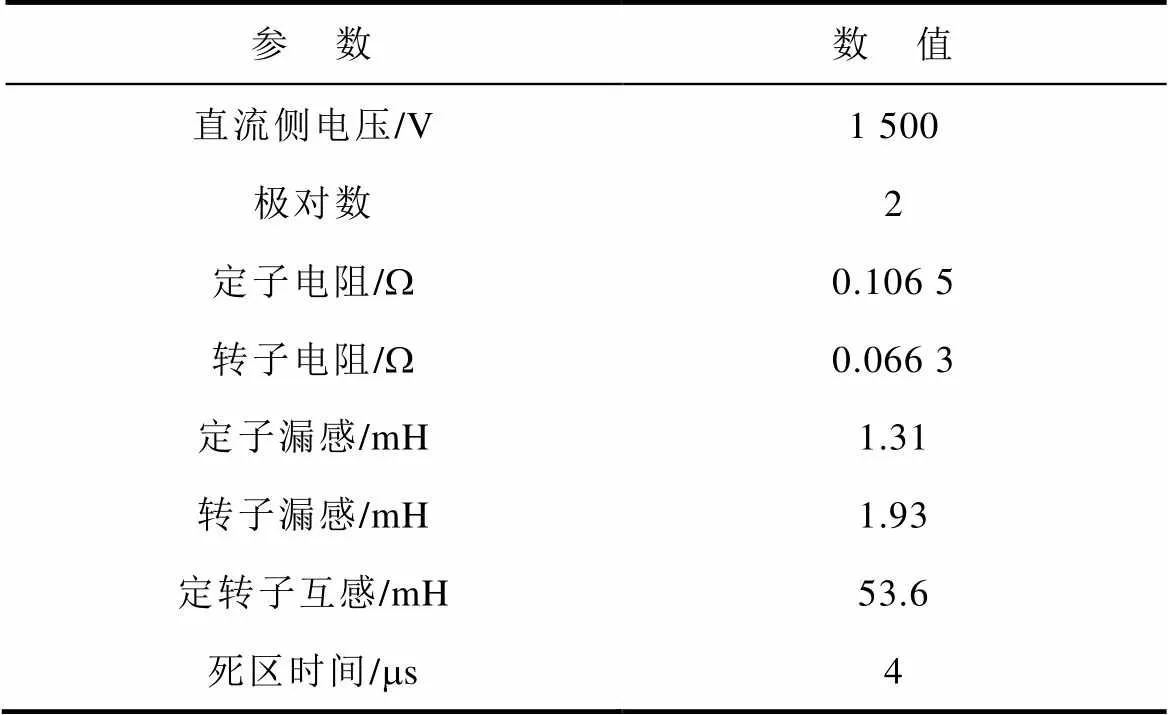
Tab.6 Parameters of Hardware-in-the-loop experiment system

图10给出了不同的同步调制模式下三相上桥臂开关管对应的PWM信号，图10a～图10f中从上至下依次为A相上桥臂PWM信号、B相上桥臂PWM信号、C相上桥臂PWM信号，其中图10a为逆变器输出频率0=50Hz时九脉冲调制模式对应PWM信号，图10b为逆变器输出频率0=52Hz时七脉冲A调制模式对应PWM信号，图10c为逆变器输出频率0=60Hz时七脉冲B调制模式对应PWM信号，图10d为逆变器输出频率0=70Hz时五脉冲A调制模式对应PWM信号，图10e为逆变器输出频率0=80Hz时五脉冲B调制模式对应PWM信号，图10f为逆变器输出频率0=100Hz时三脉冲调制模式对应PWM信号。由图10可知，本文所给出的同步调制模式对应的PWM信号具有良好的三相对称性、半波对称性以及四分之一对称性。

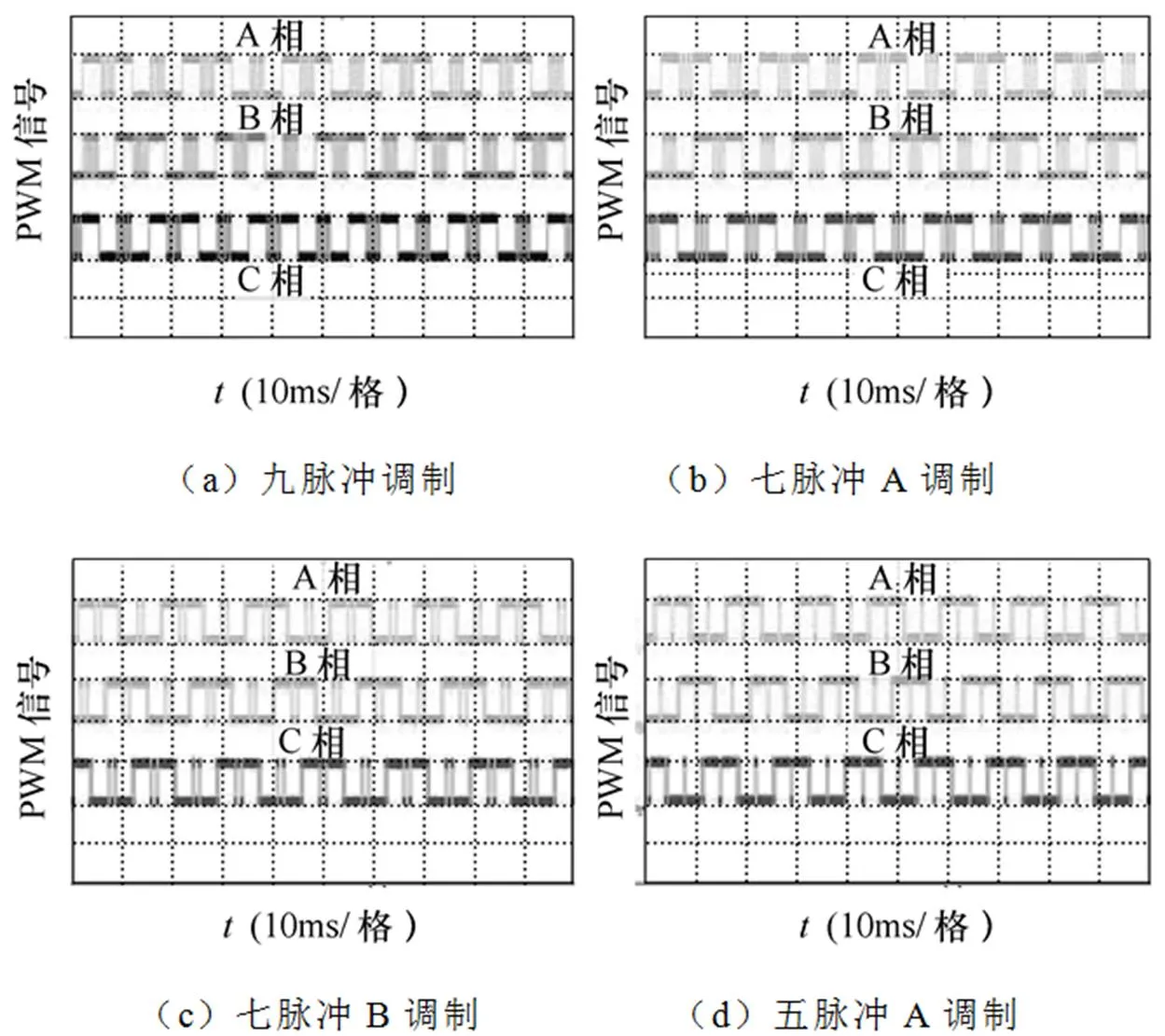
图11给出了逆变器输出频率为20Hz，开关频率为450Hz时异步调制对应的电机侧线电压AB及相电流A的波形，电流波形的半波、三相对称性好；由线电压波形可以看出，此时一个调制周期内脉冲数较多，且正负半周脉冲数相等。

图11 f=20Hz时异步调制模式下线电压和相电流的半实物实验波形

图12给出了逆变器输出频率为50Hz时九脉冲同步调制对应的电机侧线电压AB及相电流A的波形，此时电流波形满足三相对称性、半波对称性、四分之一对称性；线电压正负半周脉冲个数一致，正负半周对称性好。

图12 f=50Hz时九脉冲同步调制模式下线电压和相电流的半实物实验波形

图13给出了逆变器输出频率为52Hz时七脉冲A同步调制和60Hz时七脉冲B同步调制对应的电机侧线电压AB及相电流A的波形。此时电流波形正弦度较高，三相对称性、半波对称性及四分之一对称性均较好。

（a）=52Hz时七脉冲A同步调制

（b）=60Hz时七脉冲B同步调制

图13 七脉冲A和七脉冲B同步调制模式下线电压和相电流的半实物实验波形

Fig.13 HIL experimental waveforms of the line-voltage and phase-current in seven-pulse A and B synchronous modulation modes

图14a给出了异步调制切换到九脉冲同步调制对应的三相相电流波形。图14b给出了九脉冲同步调制切换到七脉冲A同步调制对应的三相相电流波形。图14c给出了七脉冲A同步调制切换到七脉冲B同步调制对应的三相相电流波形。图14d给出了七脉冲B同步调制切换到五脉冲A同步调制对应的三相相电流波形。由图14可知，在切换点附近，三相相电流过渡平滑，不存在明显的尖峰与跳变，并且在整个切换过程中保持了良好的三相对称性、半波对称性与四分之一对称性。

（a）异步调制切换到九脉冲同步调制

（b）九脉冲同步调制切换到七脉冲A同步调制

（c）七脉冲A同步调制切换到七脉冲B同步调制

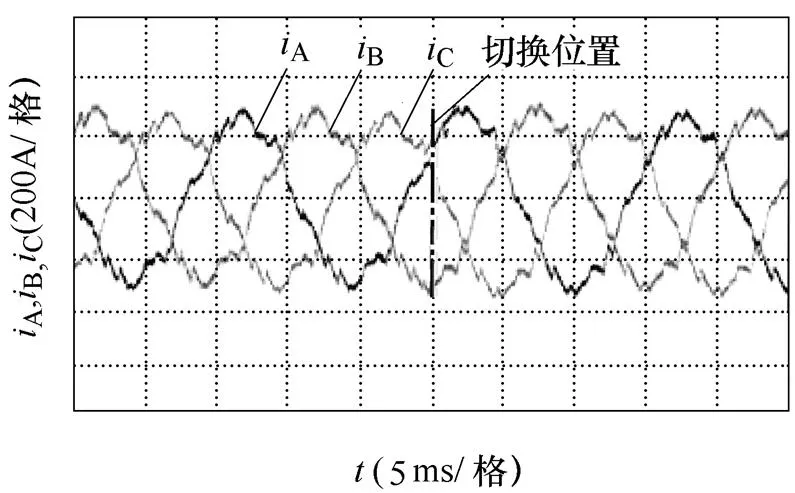
（d）七脉冲B同步调制切换到五脉冲A同步调制

图14 调制方式切换时刻相定子电流的半实物实验波形

Fig.14 HIL experimental waveforms of three-phase stator currents in the different modulation change modes

6 结论

本文以两电平牵引逆变器调制算法为研究对象，给出了一种适用于全速域的在线计算多模式SVPWM算法并给出了基于FPGA的实现方案，其特点如下：

1）该算法是一种在线计算的多模式SVPWM算法，不仅能够实现全速域范围内的调速，同时能够完成实时计算，适应各类不同的外部复杂条件。

2）从实验结果中可以看出，该算法不仅具有良好的稳态性能，同时在切换时刻具有良好的平滑切换能力。

3）方案采用VerilogHDL语言完成设计，通过简化乘法器、开方器等关键性设计在满足设计精度的前提下进一步减少芯片资源占用量，在一定程度上降低了系统的生产成本。

4）本设计可作为电机控制系统协同处理器，将SVPWM相关运算移植到FPGA中完成，使DSP/ MCU从大量正余弦计算中解放出来，更好地运行电机控制核心算法。

最后，通过半实物实验验证了所给出的在线计算多模式SVPWM算法的正确性与可行性，为牵引传动系统的设计提供了参考，对我国轨道交通牵引传动控制系统的发展具有积极意义。

参考文献

[1] 冯晓云. 电力牵引交流传动及其控制系统[M]. 北京: 高等教育出版社, 2009.

[2] Jae A, Chang H, Dong S. A new simplified space- vector PWM method for three-level inverters[J]. IEEE Transactions on Power Electronics, 2001, 16(4): 545-550.

[3] Pou J, Boroyevich D, Pindado R. New feed forward space-vector PWM method to obtain balanced AC output voltages in a three-level neutral-point-clamped converter[J]. IEEE Transactions on Industrial Elec- tronics, 2002, 49(5): 1026-1034.

[4] 姜卫东, 王群京, 史晓峰, 等. 一种完全基于两电平空间矢量调制的三电平空间矢量调制算法[J]. 电工技术学报, 2009, 24(1): 108-114.

Jiang Weidong, Wang Qunjing, Shi Xiaofeng, et al. SVPWM strategy for three-level inverter based on SVPWM strategy for two-level inverter[J]. Transa- ctions of China Electrotechnical Society, 2009, 24(1): 108-114.

[5] 韦克康, 郑琼林, 周明磊, 等. 低开关频率下混合脉宽调制方法研究[J]. 北京交通大学学报, 2011, 35(5): 106-112.

Wei Kekang, Zheng Qionglin, Zhou Minglei, et al. Study on a hybrid PWM method under low switching frequency[J]. Journal of Beijing Jiaotong University, 2011, 35(5): 106-112.

[6] 孙鹤旭, 荆锴, 董砚, 等. 基于120°坐标系的SVPWM算法研究[J]. 电工技术学报, 2016, 31(5): 52-57.

Sun Hexu, Jing Kai, Dong Yan, et al. Research of SVPWM algorithm based on 120° coordinates system[J]. Transactions of China Electrotechnical Society, 2016, 31(5): 52-57.

[7] 周明磊, 游小杰, 王琛琛. 电力机车牵引电机在方波下的控制策略[J]. 电工技术学报, 2013, 28(11): 155-162, 169.

Zhou Minglei, You Xiaojie, Wang Chenchen. Vector control of driving system of locomotive[J]. Transa- ctions of China Electrotechnical Society, 2013, 28(11): 155-162, 169.

[8] Li L, Czarkowski D, Liu Y, et al. Multilevel selective harmonic elimination PWM technique in series- connected voltage inverters[J]. IEEE Transactions on Industrial Applications, 2000, 36(1): 160-170.

[9] Pontt J, Rodriguez J, Huerta R. Mitigation of noneli- minated harmonics of SHEPWM three-level mul- tipulse three-phase active front end converters with low switching frequency for meeting standard IEEE- 519-92[J]. IEEE Transactions on Power Electronics, 2004, 19(6): 1594-1600.

[10] Agelidis V, Balouktsis A, Balouktsis I, et al. Multiple sets of solutions for harmonic elimination PWM bipolar waveforms: analysis and experimental verify- cation[J]. IEEE Transactions on Power Electronics, 2006, 21(2): 415-421.

[11] Zhang Y, Zhao Z, Zhu J. A hybrid PWM applied to high-power three-level inverter-fed induction-motor drives[J]. IEEE Transactions on Industrial Elec- tronics, 2011, 58(8): 3409-3420.

[12] Kavousi A, Vahidi B, Salehi R, et al. Application of the bee algorithm for selective harmonic elimination strategy in multilevel inverters[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1689-1696.

[13] Bowes S, Clark P. Regular-sampled harmonic- elimination PWM control of inverter drives[J]. IEEE Transactions on Power Electronics, 1995, 10(5): 521- 531.

[14] 张志刚, 黄守道, 胡存刚, 等. 三电平SHEPWM与SVPWM混合控制策略及其矢量平滑切换方法的研究[J]. 电工技术学报, 2015, 30(14): 342-348.

Zhang Zhigang, Huang Shoudao, Hu Cungang, et al. Hybrid method of three-level SHEPWM and SVPWM and its vector smooth-switching[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 342-348.

[15] 王堃, 游小杰, 王琛琛, 等. 低开关频率下SHEPWM和SVPWM同步调制策略比较研究[J]. 电工技术学报, 2015, 30(14): 333-341.

Wang Kun, You Xiaojie, Wang Chenchen, et al. Research on the comparison of synchronized modulation of SHEPWM and SVPWM under low switching frequency[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 333-341.

[16] Bowes S, Grewal S. Novel space vector based harmonic elimination inverter control[J]. IEEE Transactions on Industrial Applications, 2000, 36(2): 549-557.

[17] 何亚屏, 文宇良, 徐峻峰, 等. 基于多模式SVPWM算法的永磁同步牵引电机弱磁控制策略[J]. 电工技术学报, 2012, 27(3): 92-99.

He Yaping, Wen Yuliang, Xu Junfeng, et al. High- power permanent magnet fiux-weakening strategy based on multi-mode SVPWM[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 92-99.

[18] 徐文波, 田耕. Xilinx FPGA开发实用教程[M]. 北京: 清华大学出版社, 2012.

[19] Pongiannan R, Paramasivam S, Yadaiah N. Dyna- mically reconfigurable PWM controller for three- phase voltage-source inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(6): 1790-1799.

[20] Alvarez J, Lopez O, Freijedo F, et al. Digital parameterizable VHDL module for multilevel multiphase space vector PWM[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9): 3946-3957.

[21] 吴瑕杰, 王顺亮, 宋文胜, 等. 基于FPGA的三电平空间矢量脉宽调制算法半实物实验方案[J]. 电力系统自动化, 2014, 38(3): 78-82.

Wu Xiajie, Wang Shunliang, Song Wensheng, et al. Hardware-in-the-loop experiment scheme for a three-level space-vector PWM algorithm based on FPGA[J]. Automation of Electric Power System, 2014, 38(3): 78-82.

An On-Line Calculation Multi-Mode SVPWM Algorithm and Implementation Based on FPGA

111,2

（1. School of Electrical Engineering Southwest Jiaotong University Chengdu 610031 China 2. State Key Laboratory of Traction Power Southwest Jiaotong University Chengdu 610031 China）

Due to the low switching frequency in high power AC electrical locomotive, multi-mode modulation algorithm is widely adopted for traction inverter in the whole speed range. A new on-line calculation multi-mode space vector pulse width modulation (SVPWM) is adopted for two-level diode neutral point clamped (NPC) inverter, and the switching method between different modes is studied. Then, based on field programmable gate array (FPGA), the implementation scheme is presented, with the features of high speed, high reliability and reuse-ability. As a result, digital signal processors (DSP) can be relieved from heavy computation task through the simplified design of multiplier, square root units and divider. Finally, by virtue of hardware-in-loop (HIL) experimental system based on DSP-FPGA controller and RT-LAB platform, the accuracy of the on-line calculation multi-mode SVPWM algorithm and the feasibility of the implementation scheme are verified.

Space vector pulse width modulation, on-line, multi-mode, field programming gate array (FPGA)

TM922；TM46

吴瑕杰 男，1989年生，博士研究生，研究方向为电力电子与电力传动。

E-mail: xiajie_wu@126.com

宋文胜 男，1985年生，博士，讲师，硕士生导师，研究方向为电力牵引交流传动及其控制。

E-mail: songwsh@swjtu.edu.cn（通信作者）

2015-09-23 改稿日期 2016-05-23

国家自然科学基金（51207131、51277153）和中央高校基本科研业务费专项资金（2682013ZT19、2682013CX017）资助项目。