基于扰动观测器的永磁同步电机预测电流控制

易伯瑜 康龙云 冯自成 黄志臻



基于扰动观测器的永磁同步电机预测电流控制

易伯瑜1,2康龙云2冯自成2黄志臻2

（1. 上海央腾汽车电子有限公司 上海 2102102. 华南理工大学电力学院 广州 510640）

基于面贴式永磁同步电机（SMPMSM）离散数学模型，提出一种无差拍预测电流控制方法。为补偿模型误差以及电压型逆变器死区时间对电流控制精度的影响，设计两个并行的扰动观测器来实时估计模型不确定项及由死区时间和逆变器非线性所引起的扰动电压，并证明了其稳定性。实验结果表明，基于预测电流控制算法的电流环具有良好的动态性能，观测器通过补偿参数摄动及死区时间的影响，使算法具有很好的鲁棒性并抵制了电流谐波分量。

面贴式永磁同步电机 预测电流控制 死区时间 扰动观测器

0 引言

永磁同步电机因具有诸多优点，目前已广泛运用于工业现场、机器人控制、电动汽车等场合[1,2]。与之对应，研究人员开发了各类永磁同步电机控制技术，其中，传统的双闭环PI控制方法因设计简单、动静态性能良好而得到了广泛的应用。但PI控制器是根据误差量进行调整控制，且数字控制系统中存在电流电压采样、脉宽调制占空比更新、逆变器输出等延时环节，使得传统的PI控制方法存在滞后性，这样就会损失一定的过渡动态性能，也存在对控制器参数依赖度高的问题[3,4]。为此，有专家提出一种属于线性控制方法范畴的预测电流控制方法，因其具有高动态性能、低电流谐波分量而得到了广泛关注和研究。

目前较为流行的预测电流控制方法分为以下几种[5-8]：①提出一个代价函数，根据电压型逆变器7种不同的电压矢量来评估这一代价函数，根据代价最优原则选择一个电压矢量并将其作为电机的输入电压，这一方法设计简单，但仅有7种控制矢量，控制误差较大，无法达到满意的控制精度和谐波分量；②通过预测下一个开关周期开始时刻的参考定子电流，并采样当前控制周期的定子电流，基于永磁同步电机模型方程计算对应的电压指令值，并用SVPWM方法合成电压矢量，将指令值转换成对应的开关管占空比，使输出电流在下一个周期等于给定的参考电流。这种基于无差拍思想的控制方法可以达到满意的电流动态特性和较小的电流谐波。

但预测控制需要精确的对象模型才能输出准确的控制行为[9,10]，而电机控制对象是一个时变系统。在实际运行过程中，电机本体温度会有一定程度的升高，而对温度非常敏感的定子电阻值和转子磁链值都会随之变化。且离散电机方程是非线性电机方程的近似离散线性化，忽略相应的高次项会存在一定的模型误差。这样采用标称方程计算得出的电压指令值就会在一定程度上偏离实际所需的电压值，从而无法很好地控制电流精度。因此，如何补偿模型误差成为高精度电流控制的关键。有学者引入积分补偿技术[11]，取得了一定效果。但积分增益的选择较为困难，需要反复调整才能达到较为满意的过渡性能。D. H. Yim等[12]将不确定项设为变量，并设计了相应的卡尔曼滤波器来完成观测过程，但卡尔曼滤波器计算较复杂，只有高性能的数字信号处理芯片才能满足实时运算的需要。

另外，在实际的驱动系统中，除了模型误差外，逆变器的死区时间、开关管的通态压降及直流端的电压扰动也会影响控制器的性能[13-16]，给定子电流带来一定的误差和畸变。其中，死区时间的影响最大，为此，相关学者研究了不同的死区补偿策略。早期的研究方向主要基于固定电压技术[17]，通过死区时间、脉宽调制（Pulse Width Modulation, PWM）周期以及直流母线电压值估算出所损失部分的电压值，然后将这部分电压值加入到空间电压PWM的各相电压指令值中实现补偿。该方法实现简单，但没有考虑零电流钳位问题，性能有待提高。为解决这一问题，王庆义[18]提出由电压矢量位置结合功率因数角计算电流矢量位置，在理想电流过零点对应的空间角度设置角度阈值，阈值区间内进行线性时间补偿。但这种方法并没有考虑逆变器开通关闭、开关管导通压降等非线性因素的影响。为此，能够实现在线实时观测并进行自适应补偿的方法开始得到关注。S. Y. Kim等[19]采用观测器的方法对逆变器死区效应进行在线补偿，该方法把逆变器死区、开关器件的非理想特性及其他无法建模的因素等所产生的转子交、直轴电压作为干扰电压进行在线估计，并前馈到逆变器参考电压进行补偿，采用该方法可以得到较好的补偿效果。

本文提出一种带双观测器的预测电流控制器。将电机模型的不确定项作为待估扰动项，通过设计相应的降阶扰动观测器观测其值，并将观测值补偿到输出电压指令值中。同时，为了补偿死区效果，基于单相电流方程设计一种新颖的辅助观测器用于死区电压的估计。通过两个观测器的协同工作，实现对模型不确定项及死区时间的补偿作用，并完成了对两种观测器稳定性的证明。在基于TMS320C6713的面贴式永磁同步电机上进行实验，验证了这种并行双观测器结构的可行性。

1 预测电流控制方法

1.1 电压方程

假设磁路不饱和，空间磁场呈正弦分布，不计磁滞和涡流损耗影响，永磁同步电机在两相旋转dq坐标系的方程为[20]

考虑到电机方程在dq旋转坐标轴上的不确定扰动项，并将之定义为d和q，则式（1）可写成

式中

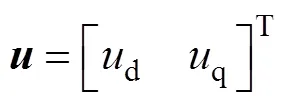
为了满足数字控制的要求，将式（2）离散化，可得

其中

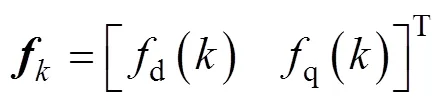
1.2 预测电流控制算法

根据电机离散电压方程，可得出预测电流控制算法，相应的电压指令值计算式为

对于面贴式永磁同步电机而言，要达到最大转矩电流比需要满足，所以直轴电流在下一个控制周期的期望给定值始终为，而交轴电流在下一个控制周期的期望值通过速度环PI控制器产生。预测电流控制的系统结构框图如图1所示。

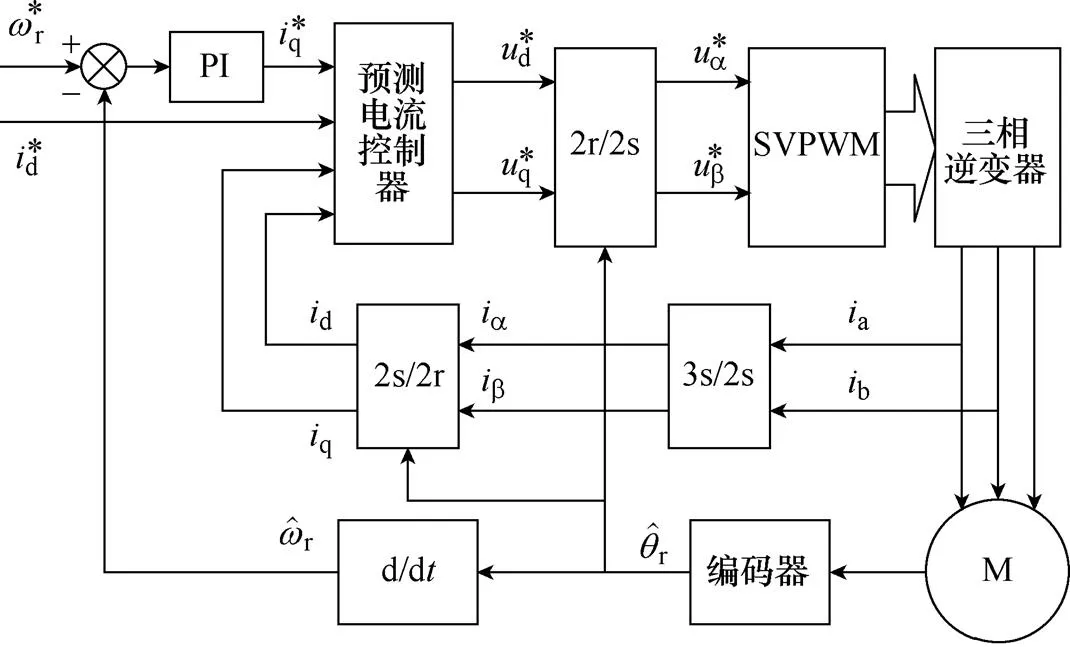
图1 预测电流控制系统结构框图

需要注意的是，在电机起动或转矩突变的情况下，由于速度环PI控制器给出的电流期望值可能较大，这样通过电压方程计算得出的电压指令值也较大，往往超出逆变器所能输出的最大电压。>因此，必须对通过预测模型计算出的指令电压值进行限制。当直流母线电压为DC时，在同步旋转坐标系下能输出的最大电压矢量值为。因此，在得出相应的电压指令值、后，计算相应的定子电压矢量值。当时，需要对电压指令值进行调整，即

2 扰动观测器设计

2.1 不确定项扰动观测器

考虑到算法的复杂性、运算量以及实现的难易程度，设计一种线性降阶观测器来估计模型不确定项。将不确定项作为状态量，建立状态方程为

其中

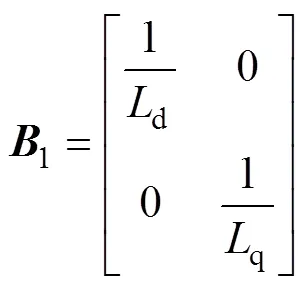
式中，上标“^”表示估计量。

根据上面的状态方程，降阶的观测器设计为

由于电流中高频噪声的存在，在观测器中直接使用电流微分值会破坏观测器的稳定性，因此，需要作状态变换，定义一个新的状态量，即

对式（9）进行求导，可得

可以看出，在的微分项中，成功消除了电流的微分项。通过式（10）得出后，再根据式（9）

2.2 稳定性

考虑扰动项动态方程，定义李雅普诺夫函数为

式中，e为扰动项的观测误差，，其微分项为

对微分可得

由于不确定项是一个缓慢变化量，可以取，代入式（15），可得

则式（16）进一步简化为

将式（12）用范数表示并代入式（18），则

根据的定义，则

2.3 G矩阵配置

如果假设12和21均为0，从而可得对角矩阵为

3 死区补偿扰动观测器

3.1 稳定性

首先讨论死区时间对逆变器输出电压的影响。在每一相电流为正和为负的时候，死区时间的作用是相反的，需要分别展开讨论。设on、off分别为开通和关断延时时间。

以a相为例，当a相电流为正值时，导通时间误差为

式（28）、式（29）可以表示为

式中

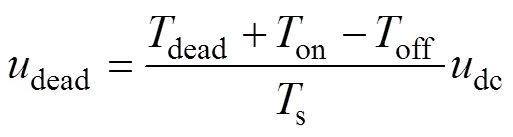
同样，其他两相的输出电压误差为

将abc三相产生的电压误差通过式（34）的坐标变换，可转换成旋转两相坐标轴上的电压误差。

式中

借助坐标变换，式（31）～式（33）中的sgna、sgnb、sgnc可以分别表示为

根据式（35）～式（37），式（34）可表示为

通过式（38）得出在dq轴上所需要补偿的电压量并加入式（4）中，实现对死区时间及逆变器非线性的补偿。

3.2 死区电压观测器及稳定性证明

通过前面分析可知，由于三相逆变器的对称性，每一相的dead值相等，可以通过其中一相计算dead，再通过式（38）得出dq轴系对应的死区电压。本文以电机定子a相的dead为对象设计观测器，首先建立a相电流为

式中，为自适应系数，＞0。

对式（42）进行微分，即

当a相电流为正且Ddead＜0时，用预测模型得出的小于实际电流值a，即a为正值，代入式（43）中，可知；如果Ddead＞0，那么用预测模型得出的大于实际电流值a，a为负值，同样会使，Ddead最终会趋近于零。当a相电流为负时，分析过程类似，可得出相同的结论，从而证明了李雅普诺夫函数的稳定性。

4 实验

采用Myway公司生产的Expert3系统进行实验，Expert3系统控制器的核心为TI公司的TMS320C6713高性能DSP控制芯片和Xilinx公司型号为SPARTAN-XC3S1500的FPGA。其中，C6713具有强大的浮点运算能力，可以满足验证各种算法的需要，主要负责核心算法计算。FPGA负责控制电路的信号采样、高速输入输出并产生PWM信号等。样机采用一台面贴式永磁同步电机，电机参数见表1。电机负载采用磁粉制动器，能提供恒定力矩，且力矩与励磁电流成线性关系。综合考虑运算精度和DSP的运算能力，实验中将逆变器开关频率设为10kHz，死区时间设为4ms。电机采用多摩川2 500线的增量编码器来读取转子的真实位置，作为估算转子位置的参考。

表1 实验电机参数

Tab.1 Experimental motor parameters

为了测试预测电流控制器的性能，电机采用力矩模式控制。在运行过程中，将q轴电流指令值由1.2A阶跃为2.5A，d轴电流指令值保持为0不变。分别观测在传统PI控制器和预测电流控制器下的电流阶跃响应，如图2所示。由图2a可看到，在传统PI电流环控制器作用下，q轴电流在经过一个超调振荡过程后才能准确跟踪相应的指令值。与之对比，图2b中经过预测电流控制器调节的q轴电流在两个PWM周期后就实现了对指令值的跟踪。这表明，预测电流控制器比PI控制器具有更快速和精确的电流控制效果。

（a）PI控制器

（b）预测电流控制器

图2 电流阶跃实验波形

Fig.2 Experimental waveforms of current step

为了观察观测器的效果，将转矩设为3N·m，速度设为600r/min，分别观测没有补偿、仅有不确定项补偿以及完全补偿情况下的a相和dq轴电流波形。图3是两个观测器均没有加入到闭环控制中的电流波形，由于不确定项和死区时间的影响，a相电流实际值的大小偏离了指令值，并产生一定的相移，dq轴电流的实际值小于指令值，从而无法实现d=0的控制策略，也就没有达到最大转矩电流比的控制要求，造成了能量的浪费。

（a）a相电流

（b）dq轴电流

图3 无补偿电流波形

Fig.3 Current waveforms without compensation

为了补偿不确定项的影响，将扰动观测器加入到闭环中，图4是对应的电流波形。由于不确定项已实现补偿，a相电流和dq轴电流都能较好地跟踪指令值。但死区时间以及其他逆变器非线性因素的存在使电流具有一定的畸变，dq轴电流中存在较为明显的6次谐波分量。这表示扰动观测器仅能补偿不确定项的影响，而无法抑制死区时间所带来的谐波分量。

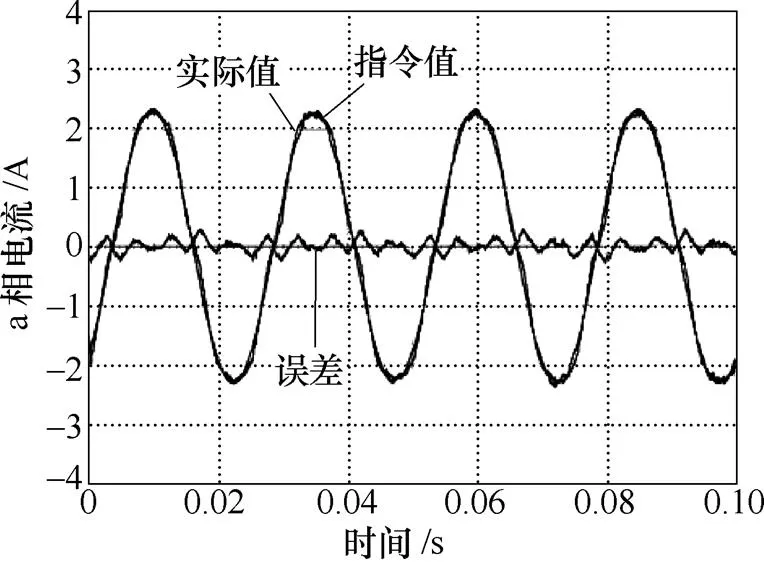
（a）a相电流

（b）dq轴电流

图4 仅有不确定项补偿的电流波形

Fig.4 Current waveforms with uncertainties compensation

图5是将两个观测器同时加入到闭环中的电流波形。从图5可以看出，实际电流值能够精确跟踪指令值，而且相应的谐波分量已得到极大削弱，从而证实了这种双观测器结构的可行性。

（a）a相电流

（b）dq轴电流

图5 完全补偿电流波形

Fig.5 Current waveforms with complete compensations

为了检验观测器的动态性能，将转矩设为2N·m，电机从静止开始起动并稳定在转速600r/min。图6是对应的实验波形。图6a中显示，由于对电流控制精确，转速在经过快速上升后，迅速稳定在设定值，没有超调量，体现了良好的动态性能和稳态精度。图6b中，由于两个观测器都有一个辨识的动态过程，在电机起步阶段还无法完成对不确定项和死区时间的辨识；在0～0.014s阶段，电流实际值无法准确跟踪指令值，并伴随有一定的电流谐波分量；经过一个短暂的过程，当观测器的补偿结果开始发挥作用后，所产生的不利影响逐渐消除，得到较好的电流控制效果。图6c和图6d是两个扰动观测器对不确定项和死区电压的辨识过程，虽然都存在少量的超调量，但对补偿效果影响不大，具备了良好的估计性能。

（a）电机速度

（b）dq轴电流

（c）不确定项

（d）死区电压

图6 电机调速实验波形

Fig.6 Experimental waveforms of speed regulation

5 结论

在面贴式永磁同步电机的两相旋转坐标轴方程下，基于无差拍控制原理，提出了无差拍预测电流控制算法。将模型中的不确定项作为扰动量进行辨识，设计降阶的扰动观测器进行观测，并将死区时间等所造成的影响折算成死区电压，设计相应的观测器进行估计，两个观测器的估计值前馈给无差拍预测电流控制器的输出电压值进行补偿。最后进行了实验验证，结果表明所提出的基于扰动观测器的预测控制算法能够精确地控制电机定子电流跟随给定电流的变化，减少了电流的谐波分量，使系统具有良好的动态和稳态性能。

参考文献

[1] 邱鑫, 黄文新, 卜飞飞, 等. 电动汽车用IPMSM直接转矩控制系统效率优化[J]. 电工技术学报, 2015, 30(22): 42-48.

Qiu Xin, Huang Wenxin, Bu Feifei, et al. Efficiency optimization of IPMSM direct torque control system used in electric vehicles[J]. Transactions of China Electrotechnical Society, 2015, 30(22): 42-48.

[2] 郭新华, 王永兴, 赵峰, 等. 基于SHEPWM的中压大功率牵引永磁同步电机两电平控制[J]. 电工技术学报, 2012, 27(11): 76-82.

Guo Xinhua, Wang Yongxing, Zhao Feng, et al. Two level control technology of PMSM used in medium voltage high power traction system based on SHEPWM[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 76-82.

[3] Mardaneh M, Bavafa F, Alavi S M S, et al. Nonlinear PI controller for interior permanent magnet synchronous motor drive[C]//2nd International Conference on Control Instrumentation and Automation, Bandung, Shiraz, 2011: 225-230.

[4] Sant A V, Rajagopal K R, Sheth N K. Permanent magnet synchronous motor drive using hybrid PI speed controller with inherent and noninherent switching functions[J]. IEEE Transactions on Magne- tics, 2011, 47(10): 4088-4091.

[5] Preindl M, Bolognani S. Model predictive direct speed control with finite control set of PMSM drive systems[J]. IEEE Transactions on Power Electronics, 2013, 28(2): 1007-1015.

[6] Moon H T, Kim H S, Youn M J. A discrete-time predictive current control for PMSM[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 464-472.

[7] Morel F, Lin-Shi X, Rétif J M, et al. A comparative study of predictive current control schemes for a permanent-magnet synchronous machine drive[J]. IEEE Transactions on Industrial Electronics, 2009, 56(7): 2715-2728.

[8] Barrero F, Arahal M R, Gregor R, et al. One-step modulation predictive current control method for the asymmetrical dual three-phase induction machine[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1974-1983.

[9] 张杰, 柴建云, 孙旭东, 等. 双三相异步电机电流预测控制算法[J]. 电工技术学报, 2015, 30(9): 12-21.

Zhang Jie, Chai Jianyun, Sun Xudong, et al. Predictive current control method for dual three phase induction machine[J]. Transactions of China Electrotechnical Society, 2015, 30(9): 12-21.

[10] 王宏佳, 徐殿国, 杨明. 永磁同步电机改进无差拍电流预测控制[J]. 电工技术学报, 2011, 26(6): 39-45.

Wang Hongjia, Xu Dianguo, Yang Ming. Improved deadbeat predictive current control strategy of permanent magnet motor drives[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 39-45.

[11] Le-Huy H, Slimani K, Viarouge P. Analysis and implementation of a real-time predictive current controller for permanent-magnet synchronous servo drives[J]. IEEE Transactions on Industrial Elec- tronics, 1994, 41(1): 110-117.

[12] Yim D H, Park B G, Kim R Y, et al. A predictive current control associated to EKF for high perfor- mance IPMSM drives[C]//26th Annual IEEE Applied Power Electronics Conference and Exposition, Fort Worth, Fort Worth, TX, 2011: 1010-1016.

[13] Sepe R B, Lang J H. Inverter nonlinearities and discrete-time vector current control[J]. IEEE Transa- ctions on Industry Applications, 1994, 30(1): 62-70.

[14] Park D M, Kim K H. Parameter-independent online compensation scheme for dead time and inverter nonlinearity in IPMSM drive through waveform analysis[J]. IEEE Transactions on Industrial Elec- tronics, 2014, 61(2): 701-707.

[15] Patel P J, Patel V, Tekwani P N. Pulse-based dead-time compensation method for self-balancing space vector pulse width-modulated scheme used in a three-level inverter-fed induction motor drive[J]. IET Power Electronics, 2011, 4(6): 624-631.

[16] Kim K H. On-line estimation and compensation scheme for dead time and inverter nonlinearity independent of parameter variations in PMSM drive[J]. International Journal of Electronics, 2012, 99(12): 1651-1674.

[17] Munoz A R, Lipo T A. On-line dead-time com- pensation technique for open-loop PWM-VSI drives[J]. IEEE Transactions on Power Electronics, 1999, 14(4): 683-689.

[18] 王庆义, 尹泉, 刘杰, 等. 一种基于定子电流重构的死区补偿技术[J]. 电力电子技术, 2006, 40(2)：73-75.

Wang Qingyi, Yin Quan, Liu Jie, et al. Dead-time compensation technique based on the reconstructed currents[J]. Power Electronics, 2006, 40(2): 73-75.

[19] Kim S Y, Lee W, Rho M S, et al. Effective dead-time compensation using a simple vectorial disturbance estimator in PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2010, 57(5): 1609-1614.

[20] Mohamed A R I. Design and implementation of a robust current-control scheme for a PMSM vector drive with a simple adaptive disturbance observer[J]. IEEE Transactions on Industrial Electronics, 2007, 54(4): 1981-1988.

Predictive Current Control for Permanent Magnet Synchronous Motor Based on Disturbance Observer

1,2222

（1. Shanghai Centem Automobile Electronics Company Limited Shanghai 210210 China 2. School of Electric Power South China University of Technology Guangzhou 510640 China）

Based on the discrete mathematical model of surface-mounted permanent magnet synchronous motors (SMPMSM), a predictive current control (PCC) scheme using dead-beat algorithm is proposed. To compensate the loss of current control precision influenced by model error and voltage-source inverter dead-time, two parallel disturbance observers are designed to estimate model uncertainty and the disturbance voltage, and their stability is proved. Experimental results show that, PCC improves dynamic performance of current loop, and disturbance observers can compensate the adverse effects of parameter variations and dead-time to make PCC more robust and have low current harmonics.

Surface-mounted permanent magnet synchronous motors, predictive current control, dead-time, disturbance observer

TM301.2

易伯瑜 男，1983年生，博士，工程师，研究方向为电动汽车电机驱动与无传感器控制。

E-mail: yiboyu@126.com（通信作者）

康龙云 男，1961年生，博士，教授，博士生导师，研究方向为可再生能源、新能源变换控制技术和新能源汽车电机驱动技术。

E-mail: lykang@scut.edu.cn

2014-08-18 改稿日期 2015-12-23

国家自然科学基金资助项目（61104181）。