稀疏表示的夏克-哈特曼波前传感器信号提取

张艳艳，许文涛，陈苏婷



稀疏表示的夏克-哈特曼波前传感器信号提取

张艳艳，许文涛，陈苏婷

( 南京信息工程大学江苏省气象探测与信息处理重点实验室，南京210044 )

由于背景噪声及探测器噪声的存在，夏克-哈特曼波前传感器质心探测误差较大，本文提出了一种在稀疏域去除背景噪声及探测器噪声的方法。首先采用二维高斯模型生成光斑信号样本图像，构造超完备目标字典，依次对测试图像分块计算其在超完备字典中的表示系数，利用噪声、背景和目标表示系数的不同，通过认为设定阈值来判别该图像块是否为光斑信号。结果表明，本文处理方法能够较好的提取出光斑信号，且与减阈值算法相比，其处理后质心偏差、RMS及PV值都较小。

自适应光学；夏克-哈特曼波前传感器；稀疏表示；质心偏差

0 引 言

夏克-哈特曼波前传感器(Shack-Hartmann wavefront sensor，S-H WFS)由于其光能利用率高、结构简单等优点，在自适应光学系统中(Adaptive Optics，AO)得到广泛的应用[1]，由于S-H WFS是通过探测子孔径的会聚光斑的强度分布来计算光斑的质心位置，而背景噪声及系统所产生的噪声对光斑的强度影响较大，导致质心误差较大，严重影响了AO系统对波前误差的校正能力[1-2]。

针对以上问题，姜文汉等人[3-5]提出减阈值的方法降低读出噪声、背景暗电流噪声等对质心探测误差的影响，但是对于一幅实际采集的图像，很难准确判断哪些像素点属于噪声、哪些属于背景、哪些是有效的光斑信号，因此对于阈值的选取一直没有统一的标准，J. Arines 和 J. Ares 等人[6]提出使用最小方差的阈值计算方法。另外，有学者[7]提出了使用加窗一阶矩的算法来计算质心，加窗法可以有效的降低窗口以外的噪声对质心探测精度的影响，通过适当改变探测窗口面积大小来降低远离光斑质心位置的像素的影响，以提高质心探测精度。但是窗口的尺寸并不能一味的减小，当光斑像素点不能全部在计算窗口内时，误差也将增大，因此在加窗法进行质心计算时，窗口尺寸的选取至关重要。K. L. Baker[8]提出了加权一阶矩算法，加权一阶矩算法利用的是光斑信号的高斯形态分布以及光斑信号的灰度值与背景及噪声信号灰度值的差别，光斑信号的灰度值要高于背景及噪声的灰度值，若将整幅图像乘以一个在光斑质心位置处高斯分布的函数，则相当于对光斑图像进行了非线性的增强。

本文提出了一种基于超完备稀疏表示的处理方法，去除背景噪声及探测器噪声，通过求解一个线性规划问题来完成提取出目标光斑及去除噪声的目的。与以往的算法相比，本文首次在稀疏域对S-H WFS图像进行噪声的处理。

1 S-H WFS光斑目标及噪声分析

含有目标的单个S-H WFS子孔径图像一般包括三部分：目标、背景及噪声，设用表示[9-10]，则：

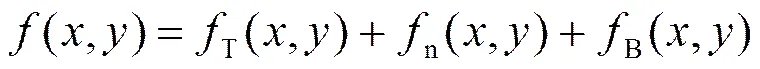
分析表明S-H WFS的主要误差源[9]为：1) CCD相机的读出噪声、包括前放和A/D采样噪声；读出噪声是均值为0，方差为的高斯噪声；2) 目标信号的光子噪声，光子噪声的分布是方差为的泊松分布的噪声；3) 天光背景噪声。天光背景噪声在不考虑系统装配误差等造成的不均匀时，其在整靶面较为均匀，略有起伏。

2 图像稀疏表示原理

根据调和分析理论，图像信号的稀疏性表述如下[11]：对于离散信号，其可以由基函数集合线性表示为

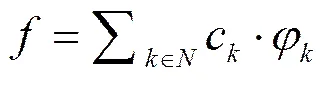
其中非零系数项越少，图像的表示就越稀疏有效。超完备字典是一种全新的信号表示理论[12]，用超完备的冗余函数库取代完备的基函数，字典中的元素被称为原子。字典的选择是提取信号的最关键步骤，选择的字典应尽可能的符合待处理的目标信号。其原理是从超完备字典中找到目标信号的最优线性组合，能够最稀疏、最佳的逼近原信号。

给定一个集合，其所有元素张成Hilbert空间，当远远大于时，称集合为超完备字典，元素作归一化处理后即为原子。对于图像信号，可以表示为个原子的线性逼近：

由于字典的冗余性，其原子之间不是线性独立的，同时图像的稀疏表示方式也不再是唯一的，因此要在满足式(3)的情况下，从各种可能的组合中选择出分解系数最为稀疏的一组解，也就是最为稀疏的表示，此时的取值最小，问题即转化为求解：

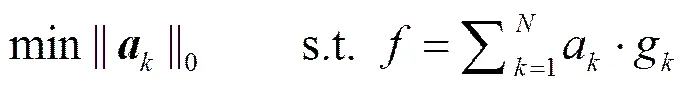
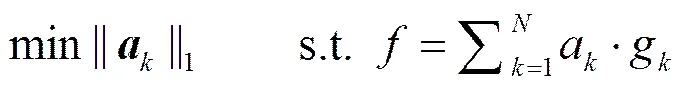
可以看出，式(5)是一个凸优化问题，可以通过线性规划算法来求解。Donoho证明[13]，当信号和超完备字典满足一定条件时，式(4)和式(5)是等价的，即式(4)的解可以通过求解式(5)来得到。

在对哈特曼图像的处理中，在构造一个超完备目标字典的基础上，依次将测试图像进行分块计算系数，分块的大小与字典原子的大小相同，并通过系数的差异来判断此图像子块是否含有光斑信号，若含有光斑信号则表示系数只有少量系数值较大，其他系数值接近于0；若该图像子块中为背景区域，则其表示系数较为均匀的，且系数值较小，也就是说，通过目标、背景及噪声在字典中的表示系数的差异，来判断该子块中是否含有光斑信号，以此达到提取目标，去除噪声的目的。

3 S-H WFS图像的稀疏表示

3.1 超完备字典的生成

光斑信号通常为小目标信号，因此本文采用二维高斯模型构造S-H WFS光斑目标的超完备字典，通过其中的各参数项，生成目标子空间，采用该模型来生成光斑目标样本图像，建立光斑信号的超完备字典，设原子大小为，其二维高斯模型如下：

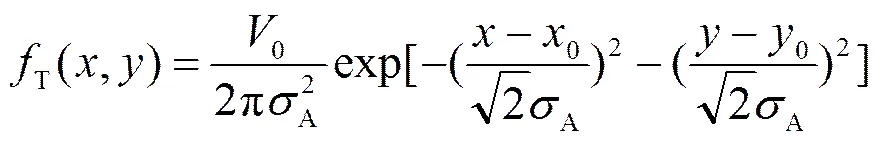
其中：表示光斑的等效高斯宽度，表示光斑的峰值强度，()表示光斑中心点的坐标。通过调节()，，四个参数来生成波前信号子图像。将样本图像展开为的一维列向量，将此向量构建为一个矩阵：

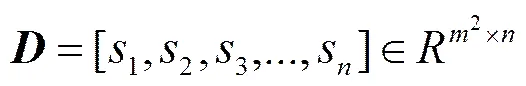
设样本的数目为，称该矩阵为超完备字典，矩阵中的每一列为超完备字典中的一个原子。图1是根据式(6)生成的样本图像及完备字典中的部分原子示意图，其中，图1(a)是根据式(6)生成的光斑目标样本，其生成条件如下：图像大小为41 pixels×41 pixels，光斑中心()坐标为(20，20)，峰值15 ADU，等效高斯宽度为＝1.25 pixels，这样模拟出的目标光斑在5 pixels×5 pixels像元内集中了80％以上的能量，可以看出，与实际的目标较为接近。图1(b)是其对应的三维能量谱图，图1(c)是根据以上原理，调节各参数所生成的字典中的部分原子。

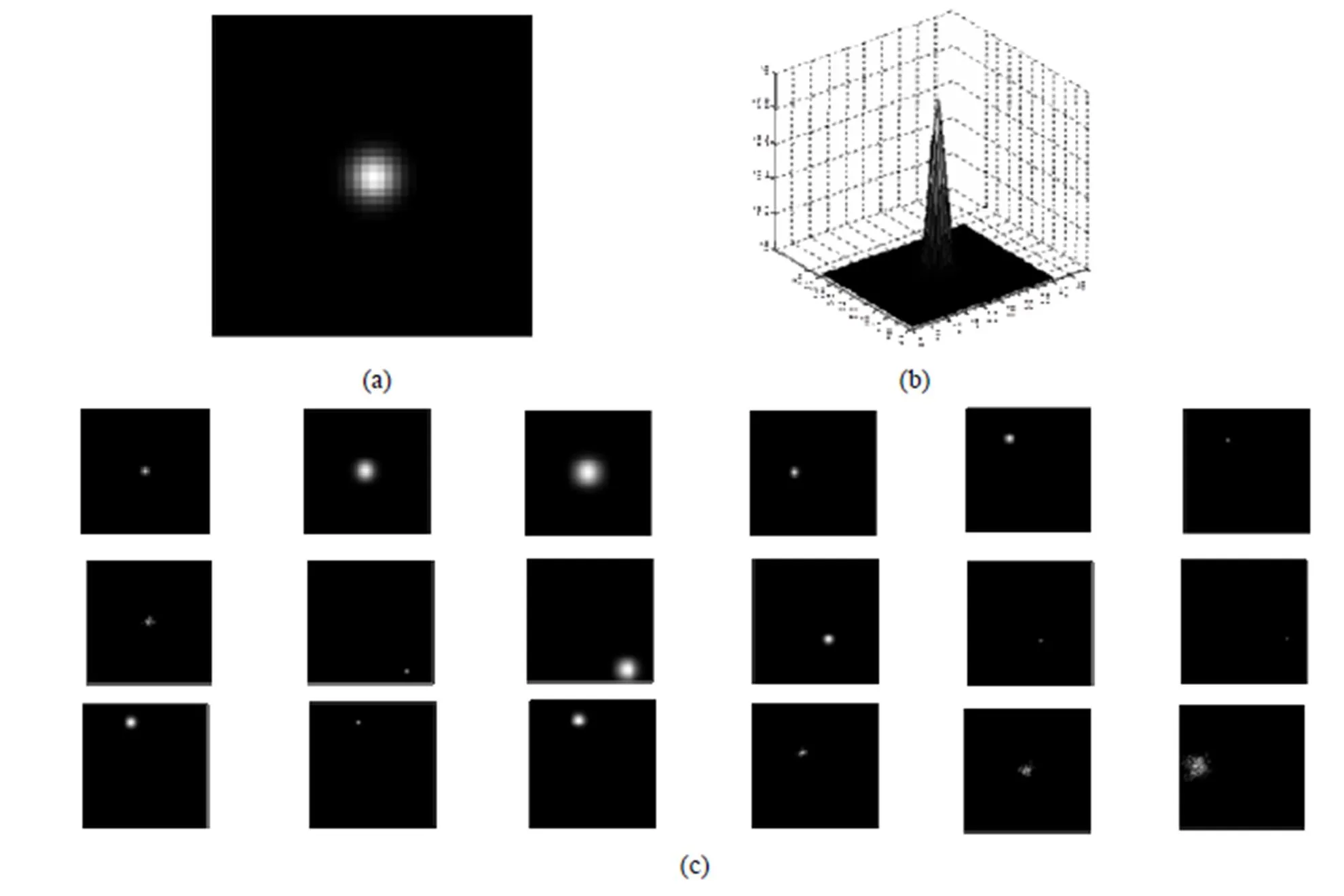
图1 目标字典示意图 (a) 字典中某原子；(b) 原子的三维能量图；(c) 字典的部分原子

(a) An atom in the over-complete dictionary; (b) The three-dimensional of the atom; (c) Part of the over-complete dictionary

3.2 基于稀疏理论的光斑信号提取算法

根据以上构造的超完备字典，将待处理的哈特曼图像进行分块，然后计算各子块在字典下的表示系数，通过比较各表示系数的差异，来判断该图像子块中是背景区域还是信号区域，从而实现去除噪声及背景、提取出光斑的目的，具体的步骤如下：

1) 利用(与原子大小相同)的滑动窗口，依次将测试哈特曼图像分割成各子块，并将其展开为维列向量。

2) 依次计算各子块的表示系数。图像子块在超完备字典中的表示系数可以通过优化式(4)或者式(5)来求解，此优化在Matlab中可以较为方便的实现。而本文中为了消除噪声的干扰，得到更加稳定的解，将以上式进行改进为式(8)，并通过此改进式求解系数。在本文中，稀疏系数的求解采用工具箱进行求解。

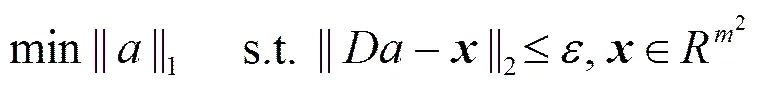
其中：是子块的向量表示，是波前信号的超完备字典，为图像子块在超完备字典中的维表示系数，为标准差，通过控制来处理不同强度的噪声。图3是在不同信噪比下的某单个子孔径中目标及噪声的稀疏系数的差别，从图中可以看出，在不含有光斑信号时系数较为均匀，在含有目标时，目标的系数与背景及噪声的系数差别较大，且信噪比越大时，对比越明显。

本文中采用均值信噪比进行描述，其定义：

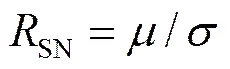
3) 建立稀疏指标矩阵。若图像子块中含有光斑信号，则求得的表示系数比较稀疏，即只有少量数值比较大，其他值均较小；若图像子块为背景或噪声，则求得的表示系数数值均比较小。从图3中可以看出，图像子块中的目标区域，其表示系数与背景及噪声区域有较大的差异。

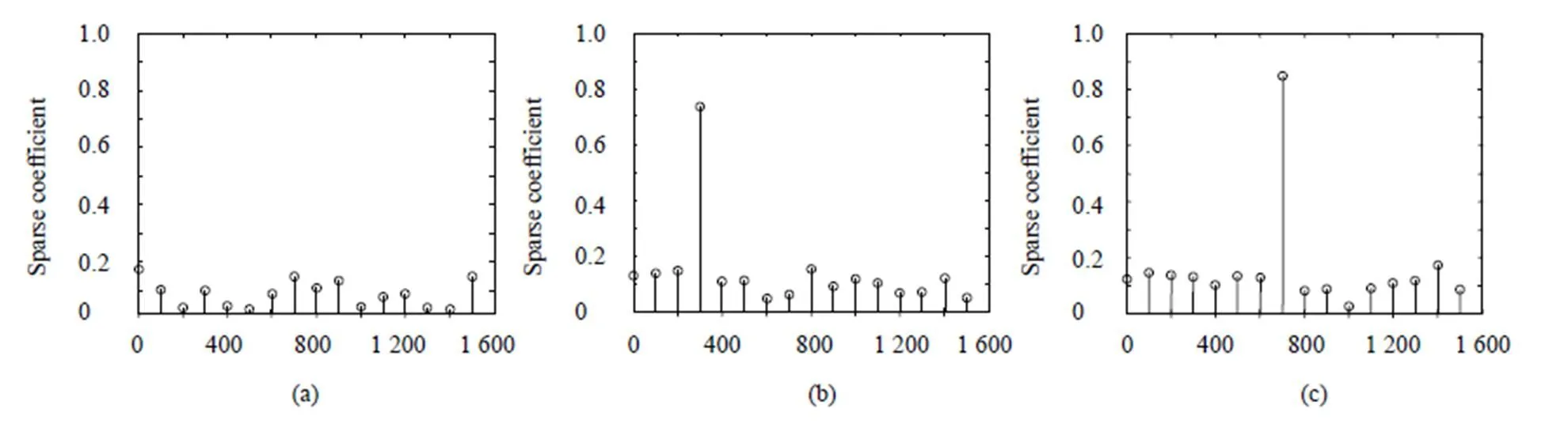
图3 (a) 不含有目标时，背景及噪声在字典中的表示系数; (b) 信噪比约为2 时目标及背景、噪声在字典中的表示系数；(c) 信噪比约为5 时目标及背景、噪声在字典中的表示系数

4) 对系数指标矩阵进行阈值处理。在稀疏程度指标矩阵中，目标所在位置具有接近于1的数值，其他位置数值均较小，在不同信噪比条件下，通常情况下，系数小于0.5，因此通过简单的阈值操作即可得到光斑信号，本文系数的阈值处理式：

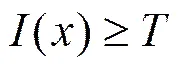
4 实验结果及分析

为了验证算法的有效性，选择多幅实验室环境所采集的S-H WFS图像进行实验，并将本文的算法处理效果与减阈值算法进行了比较。实验中，目标样本大小为16´16，阈值取0.6，CCD靶面为768 pixels´484 pixels，子孔径大小为20 pixels´20 pixels，微透镜阵列尺寸为23´23，有效子孔径数400，每一个子孔径为一个 0.51 mm的方孔，在本实验中，每一个子孔径对应焦面19 pixels。

图4(a)和图6(a)为所采集到的含噪S-H WFS图像，从图中可以看出，光斑信号几乎被背景杂波和噪声所淹没。图6较图4信噪比更低，图4(b)和图6(b)是采用本文所提出的方法处理后的结果。图5和图7是单个子孔径图像处理前后的对比图，并将其和减阈值算法进行对比。

图4 (a) 实验室采集的含有低噪声的哈特曼-夏克图像；(b) 本文算法处理后图像

图5 (a) 低噪声时处理前单个子孔径图像；(b) 减阈值效果图；(c) 本文算法处理后结果

图6 (a) 实验室采集的含有较高噪声的哈特曼-夏克图像；(b) 本文算法处理后图像

图7 (a) 较高噪声时处理前单个子孔径图像；(b) 减阈值效果图；(c) 本文算法处理后结果

为了进一步验证所提出算法的性能，将该算法与减阈值算法在不同信噪比的条件下进行了比较，并选择处理后质心偏差作为对比，从图8中可以看出，随着信噪比的提高，不管是本文算法还是减阈值算法都能够较为显著的减小质心计算的偏差，而本文算法具有较为明显的优越性。但是不可否认，本文算法运算量较减阈值算法大，实时性较减阈值差，但是该算法在理论上提供了一种新的计算思路。

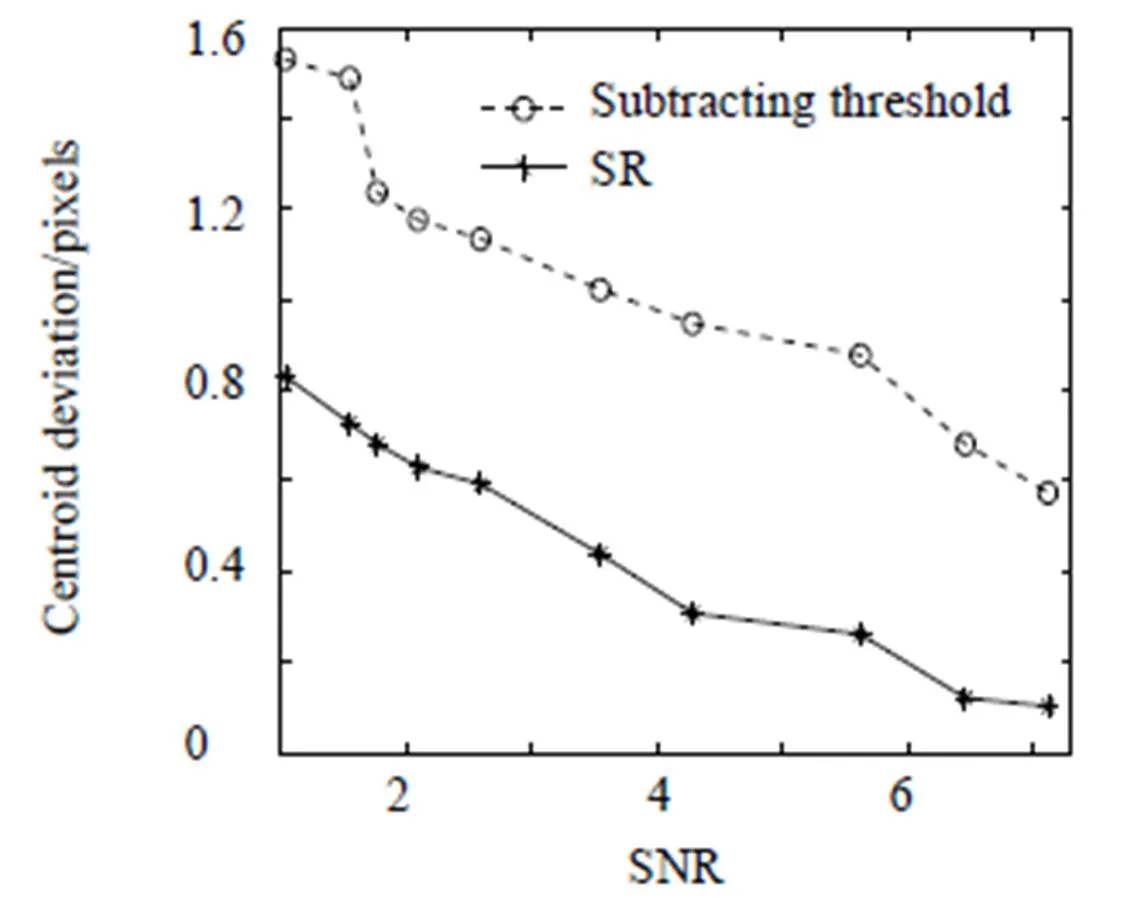
图8 不同信噪比下处理前后质心偏差曲线

另外，对不同信噪比条件下本文算法与减阈值算法处理后的质心的RMS值及PV值进行比较，如表1所示。从表中可以看到，相比于减阈值算法，所提出的算法处理后的质心起伏较小，说明本文算法的处理后的精度较好，这也与前面的主观评价结果一致。

表1 不同信噪比下减阈值算法与本文算法平均偏差RMS 及PV 比较

Table 1 The comparison of centroid deviation’s RMS and PV between sparse representation and subtracting threshold under different SNR

5 结 论

根据图像的稀疏表示理论，提出了一种新的去除S-H WFS图像噪声的方法。与减阈值算法相比，该算法利用超完备字典来表示光斑信号，首先通过二维高斯模型构造光斑信号的超完备字典，然后，计算测试图像的图像子块在超完备字典中的表示系数，图像子块中光斑信号所在的位置，其表示系数显著不同，根据此原理完成提取光斑信号的目的。最后将本文算法与减阈值算法进行了比较，并对处理后的质心偏差及质心的RMS及PV值进行了比较，结果证明了本算法处理的高精度及有效性。

[1] LI Chaohong，XIAN Hao，RAO Changhui，. Field-of-view Shifted Shack-Hartmann Wavefront Sensor for daytime adaptive optics system [J]. Optics Letters(S1539-479)，2006，31(19)：2821-2823.

[2] LI Chaohong，XIAN Hao，JIANG Wenhan，. Performance analysis of field-of-view Shack-Hartmann wavefront sensor based on splitter [J]. Applied Physics B Laser and Optics(S0946-2171)，2007，88(3)：367-372.

[3] 姜文汉，沈锋，鲜浩. 夏克-哈特曼波前传感器的探测误差 [J]. 量子电子学报，1998，15(2)：218-227.

JIANG Wenhan，SHEN Feng，XIAN Hao. Detecting Error of Shack-Hartmann Wavefront Sensor [J]. Chinese Journal of Quantum Electronics，1998，15(2)：218-227.

[4] 沈锋，姜文汉. 提高Hartmann波前传感器质心探测精度的阈值方法 [J]. 光电工程，1997，24(3)：1-8.

SHEN Feng，JIANG Wenhan. A Method for Improving the Centroid Sensing Accuracy Threshold of Hartmann Wavefront Sensor [J].Opto-Electronic Engineering，1997，24(3)：1-8.

[5] 王慎，曹根瑞. 弱光Hartmann－Shack波前传感器的阈值选取 [J]. 北京理工大学学报，2001，21(3)：348-352.

WANG Shen，CAO Genrui. Threshhold Determination of Hartmann-Shack Wavefront Sensor Operated with Faint Object [J].Transactions of Beijing Institute of Technology，2001，21(3)：348-352.

[6] Arines J，Ares J. Minimum variance centroid thresholding [J]. Optics Letters(S1539-479)，2002，27(7)：497-499.

[7] Sandrine Thomas. Optimized centroid computing in a Shack-Hartmann sensor [J]. Optics Express(S1094-4087)，2004，5490：1238-1246.

[8] Baker K L. Iteratively weighted centroiding for Shack-Hartmann wave-front sensors [J]. Optics Express(S1094-4087)，2007，15(8)：5147-5159.

[9] 张艳艳，饶长辉，李梅，等. 基于电子倍增电荷耦合器件的哈特曼-夏克波前传感器质心探测误差分析 [J]. 物理学报，2010，59(8)：5904-5913.

ZHANG Yanyan，RAO Changhui，LI Mei，. The detetin error analysis of Hartmann-Shack wavefront sensor based on electron multiplying charge-coupled devices [J].Acta Physica Sinica，2010，59(8)：5904-5913.

[10] 张锐，杨金生，田雨，等. 焦面哈特曼传感器波前相位复原 [J]. 光电工程，2013，40(2)：32-39.

ZHANG Rui，YANG Jinsheng，TIAN Yu，. Wavefront phase recovery from the plenoptic camera [J]. Opto-Electronic Engineering，2013，40(2)：32-39.

[11] Candes E，Romberg J，Tao T. Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information [J]. IEEE Transactions on Information Theory(S0018-9448)，2006，52(2)：489-509.

[12] Donoho D. Compressed sensing [J]. IEEE Transactions on Information Theory(S0018-9448)，2006，52(4)：1289-1306.

[13] Donoho D，Tsaig Y. Extensions of compressed sensing [J]. Signal Processing(S0165-1684)，2006，86(3)：533-548.

(KDXS1405)；江苏省2015大学生实践创新计划(201510300249)；江苏高校优势学科Ⅱ期建设工程资助项目

The Extraction of Signal in Shack-Hartmann Wavefront Sensor Based on Sparse Representation

ZHANG Yanyan，XU Wentao，CHEN Suting

(Jiangsu Key Laboratory of Meteorological Observation and Information Processing, Nanjing University of Information Science & Technology, Nanjing 210044, China )

Due to the background noise and the detector noise, the centroid error of Shack-Hartmann wavefront sensor is relatively large. A method to filter the noise in sparse region is proposed. First, the sample image is generated by using the two-dimension Gauss model and the over-complete target dictionary is constructed. Then, the sub-image blocks of the test image are extracted successively and the corresponding coefficients are calculated with the constructed over-complete target dictionary. Since the coefficients between the noise and the target are large different, the difference by setting a threshold is used to subtract the target. Experimental results show that, the target can be well subtracted, while the centroid deviation and the RMS and PV of the centroid are smaller than using the method of subtracting threshold.

adaptive optics; Shack-Hartmann wavefront sensor; sparse representation; centroid deviation

TN919.8

A

10.3969/j.issn.1003-501X.2016.04.008

2015-06-22；

2015-11-14

国家自然科学基金资助项目(61071164)；江苏省高校基金重大项目(12KJA510001)；江苏省气象探测与信息处理重点实验室项目

张艳艳(1983-)，女(汉族)，江苏南京人。博士，讲师，现从事信号处理工作。E-mail：002243@nuist.edu.cn。