拉盖尔-高斯光束在non-Kolmogorov湍流中传输的数值模拟

王帅会，陈家奇，顾国超



拉盖尔-高斯光束在non-Kolmogorov湍流中传输的数值模拟

王帅会，陈家奇，顾国超

( 中国科学院长春光学精密机械与物理研究所，长春130033 )

针对大气湍流对拉盖尔-高斯光束的螺旋谱的影响，本文提出利用多相位屏法模拟拉盖尔-高斯光束在大气湍流中的传输。采用傅里叶变换法模拟符合non-Kolmogorov谱的大气随机相位屏，通过改变拓扑荷、光束波长、指数参数、折射率结构常数、湍流内尺度、外尺度等参数，对大气湍流的影响进行数值模拟。仿真结果表明，大气湍流会导致拉盖尔-高斯光束的螺旋谱的弥散。而且，螺旋谱弥散与拓扑荷、波长、指数参数、折射率结构常数、内尺度、外尺度密切相关。

non-Kolmogorov湍流；相位屏；拉盖尔-高斯波束；拓扑荷

0 引 言

1992年，Allen等发现带有相位因子的光束中每个光子具有的轨道角动量[1]。这类光束称为涡旋光束，独特的相位结构使其在生物医学、信息传输领域得到了极大的重视[2-5]。与传统通信相比，利用轨道角动量进行通信可以在不增加带宽的情况下极大的提高数据传输容量，并且具有独特的保密性[6]。然而在实际应用中，由于大气湍流的随机性与不稳定性，不可避免的会引起光束的强度以及相位变化，导致误码率的增加以及通信容量的降低[8-9]。研究影响光束螺旋谱的各种因素，对于提高基于轨道角动量的通信系统性能具有重要的意义。研究大气湍流对涡旋光束影响可以采用理论分析[9-10]与数值模拟的方法[11-13]。由于湍流介质的复杂性，数值模拟方法已成为研究光束在大气湍流中传输问题的一种重要手段。张慧敏、王立瑾等人对符合Kolmogorov谱的大气随机相位屏进行了数值模拟，Anguita等人利用相位屏模拟的方法研究了拉盖尔-高斯(Laguerre-Gaussian, LG)光束在Kolmogorov湍流中水平传输的情况,Wen Cheng等人利用相位屏的方法研究了矢量涡旋光束在基于von Karman功率谱的大气湍流中的传输[14]。而利用数值模拟法研究符合non-Kolmogorov谱的相位屏以及LG光束在其中传输的情况，尚未有研究。

本文通过傅里叶变换法产生符合non-Kolmogorov谱的多相位屏，模拟LG光束在大气湍流中的水平传输，并研究拓扑荷、波长、指数参数、折射率结构常数、湍流内尺度、外尺度等参数对LG光束的螺旋谱的影响。

1 拉盖尔-高斯光束及螺旋谱

携带轨道角动量的光束有贝塞尔光束、厄米特-贝塞尔光束、LG光束等，本文以典型的LG光束为例进行研究。在柱坐标系中，LG光束的表达式为

其中：，为束腰半径，为瑞利距离，为拓扑荷，为径向指数，为连带拉盖尔多项式，为光束的曲率半径，为归一化常数。当拓扑荷不为0时，光束中心强度为零，相位为螺旋结构。

Molina-Terriza认为，任何一种光束都可以分解成一系列螺旋谐波的叠加[15]

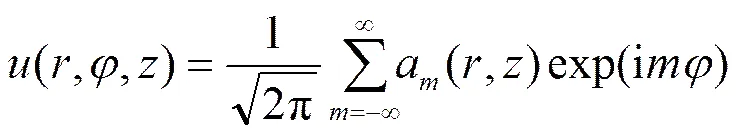
其中：且。拓扑荷的能量可以由表示，光束的总能量为，为真空中的介电常数。因此，任一光束的螺旋谐波的权重可以表示为

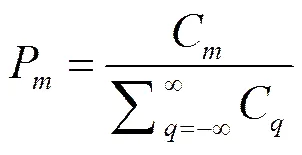
假定发送端拓扑荷为，接收端拓扑荷为；为发送端拓扑荷为时，接收端接收到拓扑荷()的概率。当光束在大气湍流中传输时，涡旋光束的螺旋谱就会发生弥散，原本只集中于一个或某几个分量上的能量会发散到其它分量上，造成码间串扰。而利用轨道角动量进行通信可以极大的提高系统的保密性和系统容量。因此，研究大气湍流对涡旋光束的螺旋谱的影响具有重要的意义。

2 相位屏的产生

数值模拟的方法是产生相位屏来模拟大气湍流。产生相位屏的方法可以分成两类：一种是根据大气湍流的功率谱密度函数得到大气畸变相位分布，称为傅里叶变换法[16]；另一种是用正交的Zernike多项式作为展开函数来描述波前相位，称为Zernike多项式展开法[17]。本文采用傅里叶变换法。傅里叶变换法的基本思想是用一个复高斯矩阵对大气湍流的功率谱进行滤波，然后通过逆傅里叶变换得到大气导致的畸变相位：

式中：是大气畸变相位，为频率域里的零均值、单位方差的复高斯随机矩阵，是大气折射率起伏引起的大气湍流的功率谱函数。对于non-Kolmogorov功率谱：

其中：为广义振幅且。指数的变化范围为。，且。为外湍流尺度，为内湍流尺度。为广义的大气湍流的折射率结构参数，表征大气湍流的强度，单位为。在水平传输时，为一固定值。那么沿方向传播的功率谱可以表示为

而大气相干长度0的表达式为

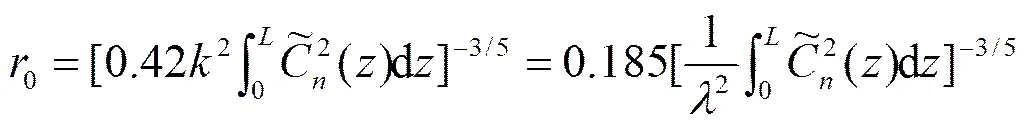
将式(7)代入式(6)可得，功率谱为

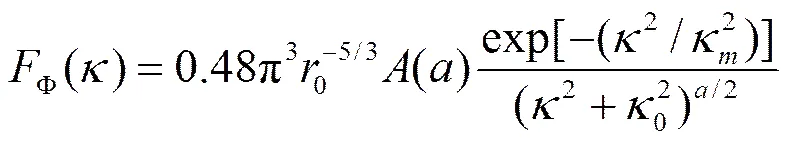
将式(8)代入式(4)并进行离散化后，得到：

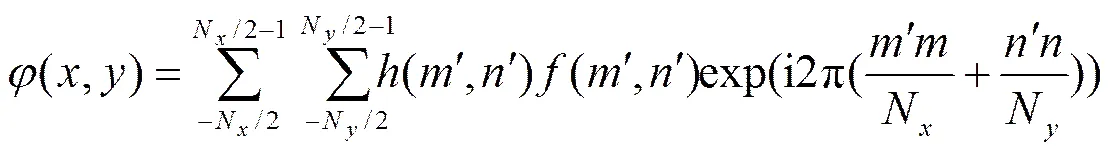
其中：，,分别为抽样点数。

3 仿真结果与分析

结合non-Kolmogorov谱模拟生成的相位屏以及利用Huygens-Fresnel原理，就LG光束在大气湍流中水平传输进行数值模拟。这里，相关参数的选择为：相位屏大小70 cm×70 cm，网格数为256×256，传播路径上相位屏间隔距离为50 m。由于径向指数不影响拓扑荷，取=0。

当=11/3，，时，non-Kolmogrov湍流退化为Kolmogorov湍流。此时，波长取1 550 nm，，0=0.01 m，，=1 km。LG光束在non-Kolmogorov湍流中传输的螺旋谱模拟值与文献[10]的理论值对比如图1所示，验证了仿真的正确性。

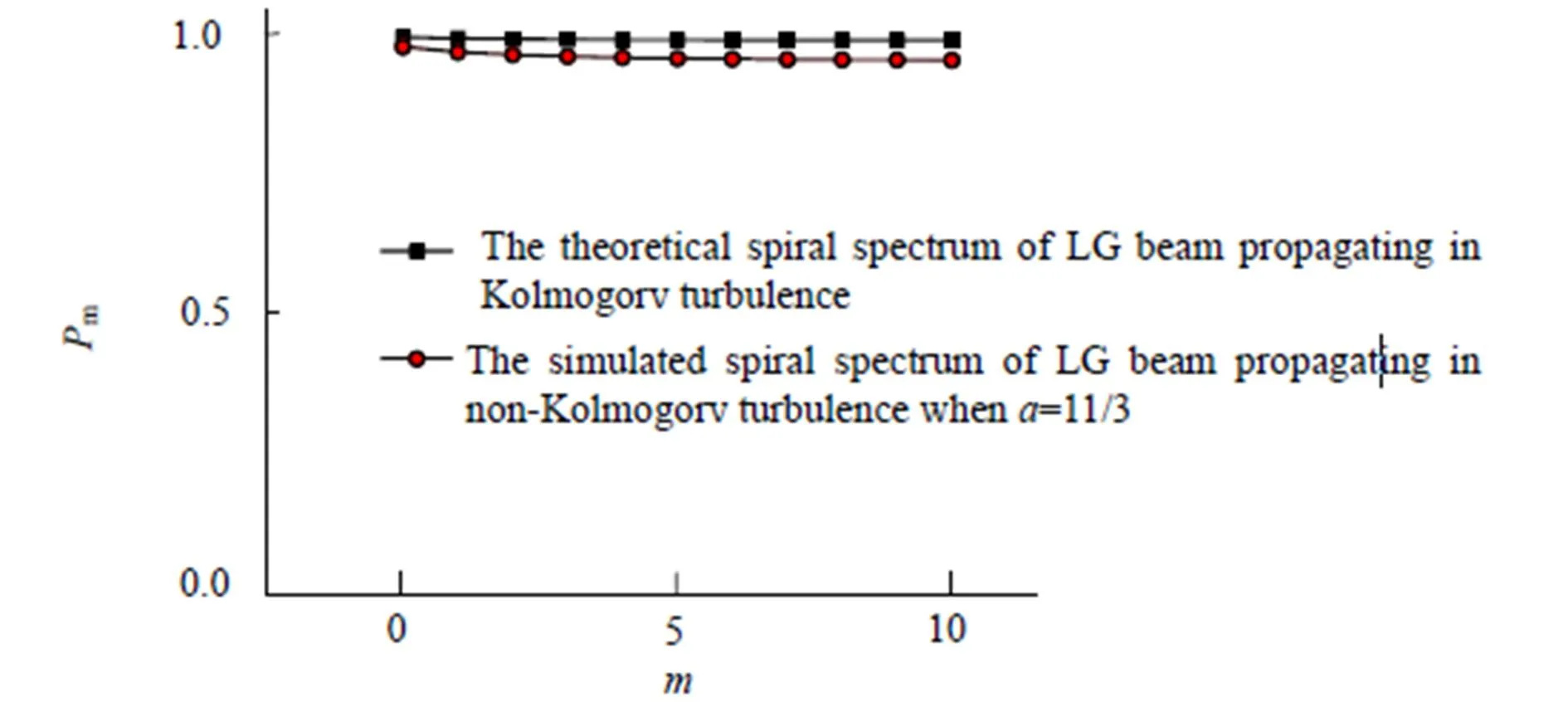
图1 LG 光束在non-Kolmogorov 湍流中传输的螺旋谱模拟值与光束在Kolmogorov 湍流中传输理论值对比

当波长分别取632.8 nm，850 nm，1 550 nm时，=3.8，其它参数保持不变，螺旋谱与激光波长的关系如图2所示。当其它条件相同时，波长越大，螺旋谱弥散得越轻微。对于同一波长，随着拓扑荷的增大，螺旋谱弥散逐渐严重。因此，虽然理论上拓扑荷可以取任意整数，拓扑荷的取值是有限制的。

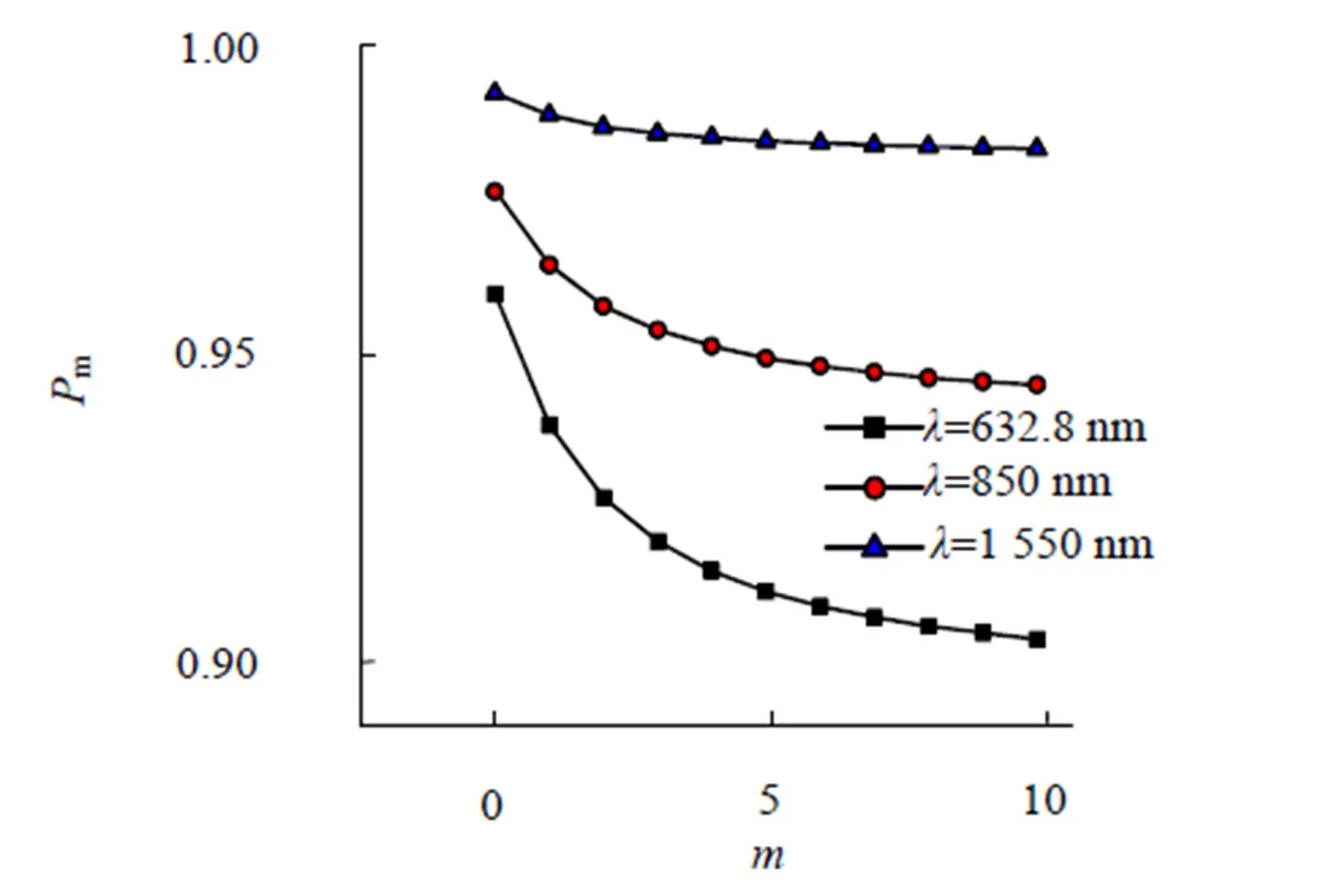
图2 不同波长的LG 光束在non-Kolmogorv湍流中传输时的螺旋谱分布

LG光束的螺旋谱与指数参数的关系如图3所示。由图可知，螺旋谱的弥散情况随着指数参数的改变而改变。首先随着指数参数的增大，螺旋谱弥散加重。当达到最低点后，螺旋谱的弥散随着的增大而减轻。这与湍流干扰项密切相关，湍流干扰项表征大气湍流的大小。

图3 LG 光束的螺旋谱与指数参数a 的关系

螺旋谱与折射率结构常数、湍流内尺度、外尺度的关系如图4所示。当折射率结构常数越大、内尺度越小、外尺度越大时，螺旋谱弥散越严重。这是因为折射率结构常数越大，湍流强度越大；更小的内尺度、更大的外尺度意味着湍流中有更多的湍流块。LG光束的螺旋谱随着湍流强大的增大而弥散加重。

图4 螺旋谱与结构常数、内尺度、外尺度的关系曲线

(a) 结构常数不同；(b) 内尺度0 不同；(c) 外尺度0 不同

Fig.4 Curve of spiral spectrum of LG beam with structure constant, inner scale and outer scale

(a) Different; (b) Different0; (c) Different0

4 结 论

本文通过傅里叶变换法产生多相位屏，数值模拟了LG光束在non-Kolmogorov湍流时各种因素对LG光束的螺旋谱的影响。仿真结果表明，螺旋谱随着拓扑荷、折射率结构常数、湍流外尺度的增大，光束波长、湍流内尺度的减小而弥散加重。螺旋谱弥散首先随着指数参数的增大而加重。当达到最低点后，螺旋谱的弥散随着指数参数的增大而减轻。仿真结果可以为激光轨道角动量通信提供一定的指导。

[1] Allen L，Beijersbergen M W，Spreeuw R J C，. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes [J]. Physical Review A(S1050-2947)，1992，45(11)：8185-8189.

[2] Gibson G，Courtial J，Vasnetsov M，. Increasing the data density of free-space optical communications using orbital angular momentum [J]. Proceedings of SPIE(S0277-786X)，2004，5550：367-373.

[3] Paterson C. Atmospheric turbulence and orbital angular momentum of single photons for optical communication [J]. Physical Review Letters(S0031-9007)，2005，94(15)：477-481.

[4] Celechovsky R，Bouchal Z. Optical implementation of the vortex information channel [J]. New Journal of Physics(S1367-2630)，2007，9(9)：328.

[5] Gbur G，Tyson R K. Vortex beam propagation through atmospheric turbulence and topological charge conservation [J]. Journal of the Optical Society of America A (S1520-8532)，2008，25(1)：225-230.

[6] Molina-Terriza G，Torres J P，Torner L. Management of the angular momentum of light：preparation of photons in multidimensional vector states of angular momentum [J]. Physical Review Letters(S0031-9007)，2002，88(1)：013601.

[7] Gibson G，Courtial J，Padgett M，Free-space information transfer using light beams carrying orbital angular momentum [J]. Optics Express(S1094-4087)，2004，12(22)：5448-5456.

[8] Bouchal Z，Celechovsky R. Mixed vortex states of light as information carriers [J]. New Journal of Physics(S1367-2630)，2004，6(1)：1-15.

（三）产业化生产阶段财税激励政策的作用。这一阶段企业需要做大量工作，如需要为新技术、新产品寻找市场，需要给企业进行大批量生产提供保障。政府在这一阶段的地位比较微妙，政府直接支持固然能直接减轻企业负担，但要避免过度干预影响市场资源配置，影响市场自身调节作用的发挥。因此，这一阶段，政府一般会采用间接手段给企业提供支持，如采用税收优惠政策或采用政府采购政策等鼓励企业进行产业化生产，通过税收优惠降低企业产业化生产成本，提高企业成本优势，或者鼓励引导社会资金进入，刺激市场对产品的需求，帮助企业回笼资金，缩短企业资本循环周期，降低企业产业化生产的风险。

[9] 黎芳，唐华，江月松，等. 拉盖尔-高斯光束在大气湍流中的螺旋谱特性 [J]. 物理学报，2011，60(1)：251-256.

LI Fang，TANG Hua，JIANG Yuesong，. Spiral spectrum of Laguerre-Gaussian beams propagating in turbulent atmosphere [J]. Acta Physica Sinica，2011，60(1)：251-256.

[10] JIANG Yuesong，WANG Shuaihui，ZHANG Jiaqi，. Spiral spectrum of Laguerre–Gaussian beam propagation in non-Kolmogorov turbulence [J]. Optics Communications(S0030-4018)，2013，303：38-41.

[11] 张慧敏，李新阳. 大气湍流畸变相位屏的数值模拟方法研究 [J]. 光电工程，2006，33(1)：14-19.

ZHANG Huimin，LI Xinyang. Numerical simulation of wavefront phase screen distorted by atmospheric turbulence [J]. Opto- Electronic Engineering，2006，33(1)：14-19.

[12] 王立瑾，李强，魏宏刚，等. 大气湍流随机相位屏的数值模拟和验证 [J]. 光电工程，2007，34(3)：1-4.

WANG Lijin，LI Qiang，WEI Honggang，. Numerical simulation and validation of phase screen distorted by atmospheric turbulence [J]. Opto-Electronic Engineering，2007，34(3)：1-4.

[13] Anguita J A，Neifeld M A，Vasic B V. Modeling channel interference in an orbital angular momentum-multiplexed laser link [J]. Proceedings of SPIE(S0277-786X)，2009，7464：0U1-6.

[14] 卫沛锋，刘欣悦，林旭东，等. 自适应光学系统测试中大气湍流的时域模拟[J]. 中国光学，2013，6(3)：371-377.

WEI Peifeng，LIU Xinyue，LIN Xudong，. Temporal simulation of atmospheric turbulence during adaptive optics system testing [J]. Chinese Journal of Optics，2013，6(3)：371-377.

[15] Torner L，Torres J，Carrasco S. Digital spiral imaging [J]. Optics Express(S1094-4087)，2005，13(3)：873-881.

[16] CHENG Wen，HAUS Joseph W，ZHAN Qiwen. Propagation of vector vortex beams through a turbulent atmosphere [J]. Optics Express(S1094-4087)，2009，17(20)：17829-17836.

[17] McGlamery B L. Computer simulation studies of compensation of turbulence degraded images [J]. Proceedings of SPIE (S0277-786X)，1976，74：225-233.

[18] Noll R J. Zernike polynomials and atmospheric turbulence [J]. Journal of the Optical Society of America A(S1520-8532)，1976，66(3)：207-211.

Numerical Simulation of Laguerre-Gaussian Beam Propagation in non-Kolmogorov Turbulence

WANG Shuaihui，CHEN Jiaqi，GU Guochao

( Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China )

In order to study spiral spectrum spread after Laguerre-Gassian (LG) beam propagating through atmospheric turbulence, the method of multiple phase screen is proposed to simulate the transmission of LG beams carrying Orbital Angular Momentum (OAM) in atmospheric turbulence. Propagation of Laguerre-Gaussian beam through atmospheric turbulence is simulated using phase screen based on Fourier transform following the non-Kolmogorov spectrum and the effect induced by atmospheric turbulence is computed quantitatively for different topological charges, wavelengths, exponent parameters, structure constant of the refractive-index fluctuations, inner scales and outer scales. The simulation results show that atmospheric turbulence deteriorates spiral spectrum of LG beam. It is also shown that system performance is closely related to topological charge, wavelength, exponent parameters, structure constant of the refractive-index fluctuations, inner scales and outer scales.

non-Kolmogorov turbulence; phase screen; Laguerre-Gaussian beam; topological charge

TN929.12

A

10.3969/j.issn.1003-501X.2016.04.004

2015-05-25；

2015-08-11

王帅会(1988-)，男(汉族)，吉林长春人。研究实习员，硕士，主要从事激光及毫米波轨道角动量方面的研究。

E-mail: wshcan912@hotmail.com。