半监督复合核图聚类在高光谱图像中的应用

李志敏，郝盼超，黄 鸿，黄 文



半监督复合核图聚类在高光谱图像中的应用

李志敏，郝盼超，黄 鸿，黄 文

( 重庆大学光电技术与系统教育部重点实验室，重庆 400030 )

针对图的半监督聚类算法(Semi-Supervised Graph-Based Clustering, SSGC)中出现的对先验信息利用不充分、不足以应对数据异构、计算耗时大等问题，本文提出一种基于半监督复合核的图聚类算法，并应用于高光谱图像。该算法首先通过引入半监督学习方法对径向基函数(Radial Basis Function, RBF)进行了改进，以充分利用少量的标记样本和无标记样本；其次将RBF核与光谱角核进行融合，构造复合核权重矩阵。在权重矩阵的构造过程中，K-近邻方法的引入也简化了计算过程。在Indian Pine和Botswana高光谱数据集上的实验结果表明，相对于SSGC算法，本文算法不仅实现了更高的分类正确率，其总体分类精度提升1%~4%，而且有效提升了运算速度。

高光谱遥感图像；聚类；半监督学习；复合核

0 引 言

高光谱遥感图像包含了丰富的空间和光谱信息，具有很高的分辨力，已应用到科学研究的各个领域，特别是国防等涉及国家安全方面[1]。然而，面对高光谱的海量数据，如何将高光谱图像的各种特征结合，研究快速、高效的目标识别算法是目前和未来一段时间内的一个重点。

聚类分析是数据挖掘及机器学习领域内的重点问题之一，在数据挖掘、模式识别、决策支持、机器学习及图像分割等领域有广泛的应用。聚类是一个将数据分类到不同的类或者簇的过程，属于同一个簇的样本或者数据的特性具有很大的相似性，属于不同簇的样本数据有较大的不同点，聚类的这一特性可在高光谱图像处理中发挥重要的作用[2]。

在聚类领域中，传统的方法分为无监督聚类和监督聚类两种。前者不需要有标记的数据，但限制了算法性能的提高；监督聚类需要大量的有标签样本的数据作为训练集，而有标记数据的获取却是比较困难且昂贵的。由于监督聚类和非监督聚类的局限性，半监督聚类成为一个新兴的研究热点。半监督聚类结合了非监督聚类和监督聚类的优点，充分利用数据的类别信息和内部结构信息，能够得到比较好的结果[3]。冷明伟[4]提出一种基于极少量标签数据的半监督K-均值聚类算法，它首先利用标签数据集选取初始点，对给定的数据集进行聚类，然后基于影响因子和约束进行聚类结果的合并，该方法在标记样本较少时仍能实现较高的聚类精度。陈小冬等[5]提出一种基于判别分析的聚类算法，迭代执行降维和聚类，其不仅能很好地处理高维数据，还有效地提高了聚类性能。

Camps-Valls[6]等提出一种基于图的半监督聚类算法(Semi-Supervised Graph-Based Clustering, SSGC)，将流形学习算法应用于图结构的设计中，能很好的挖掘高光谱遥感数据的非线性特性[7]，取得了较好的分类效果。SSGC算法相对于支持向量机(Support Vector Machine, SVM)算法表现出较好的鲁棒性和稳定性，且当标记样本数较少时，优势更加明显，这说明该方法在不适定情况下分类的有效性。通过将该方法在高光谱数据上运行，发现此算法能产生较高的分类正确率，但仍有提升空间；然而其耗时巨大，虽然原作者使用Nyström方法[8]以提升计算速度，但这种方法又引进了两个需要调节的参数——用于计算核矩阵近似分解的样本数和最大本征值的数量。

鉴于SSGC算法的不足，本文在此算法上进行一定的改进，首先通过引入半监督学习方法对RBF核函数进行了改进，更好地利用了样本的先验信息和背景知识；同时又融合光谱角核函数，最终提出一种半监督复合核图聚类算法(Semi-Supervised Graph Clustering with Composite Kernel, SSGCK )，可以提高聚类正确率，而且有效提升运算速度。

1 相关工作

1.1 半监督聚类

聚类是将不同的样本数据按照其本身的特性划分到各个不同的类或者簇的过程，它能够很好地反映样本的分布特点，揭示数据结构特征，并表现出一定的优势。较为经典和著名的聚类算法有：K-均值(K-means)算法[9-10]，一种将样本以隶属度为1或0的方式划分至某一类中的硬划分聚类算法，已被广泛使用；模糊C-均值(Fuzzy C-Means，FCM)算法[11-12]，Bezdek将模糊因子引入了K-均值算法，提出了FCM算法。

半监督聚类[13]利用少部分标记的数据辅助非监督的学习。目前，半监督的聚类方法大致分为以下两类：

1) 基于限制的方法。该类算法在聚类过程中，利用标签的数据来引导聚类过程，最终得到一个恰当的分割结果。通过分析给定的标记信息和其它相关的约束条件，得到更多控制聚类过程的信息，减少聚类搜索的次数或者盲目性，在得到更好聚类效果的同时能适当减少聚类的时间。

2) 基于距离测度函数学习的方法。聚类算法必须基于某一距离测度函数进行聚类，在该方法中所使用的距离测度函数是通过对标签数据学习得到的。

1.2 SSGC算法

SSGC算法是一种基于图的半监督聚类算法。基于图的半监督聚类算法核心思想在于：构造一个图模型(，)，图中数据点作为顶点，数据的相似性作为边权值。其中数据节点包含了少量有标记的数据和大量无标记的数据，边权值反映了数据点之间的相似程度，权值越大表示数据点越相似，反之越不相似。SSGC算法的具体实现为：

假设存在个维数据空间的数据组成的数据集={1,2, …,,+1, …,}Ì以及其对应的标签集{1, 2, 3, …,}，其中前个数据点被标记为Î，其余数据为未标记数据，目标算法就是找到这个数据点所属的类别。定义一个的矩阵，若数据中第个点被标记为=jÎ，则=1，否则=0；在计算之前，首先引入标记样本信息，即仿照定义的方式定义一个×的矩阵，将数据集中已知类别的标记信息代入中。

SSGC算法的重点是构造近邻矩阵，其使用的是RBF核函数：

式中令=0以避免自相似。

2 半监督复合核图聚类算法

SSGC算法在构造近邻矩阵时，必须求出每个点相对于其他所有点的权重值，这是一个繁琐而又冗余的操作，而且SSGC算法在此过程没有应用标记样本信息；另外，SSGC算法采用单个核函数构成的核机器并不能应对诸如数据异构或不规则、样本规模巨大、样本不平坦分布等实际问题。

本文提出的SSGCK算法在构造权重矩阵时，先对RBF核函数进行一定的改进，精简算法步骤，减少计算量，同时加入标记信息，增加同类点权重，构造出第一个权重矩阵；然后又利用光谱角信息，构造了一个基于光谱角核函数的权重矩阵，最后将两个权重矩阵融合，构造复合核函数权重矩阵。最后研究基于此复合核权重矩阵的聚类，得到了很好地实验效果。

复合核函数的本质就是将个核函数组合起来，事实上任一函数只要满足Mercer条件[14-15]，就可以看作是一种核函数。假设一组基核函数，则总函数定义如下：

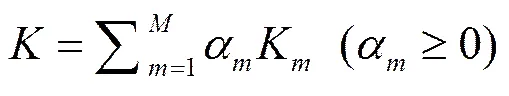
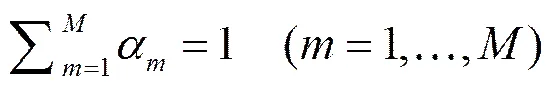
多核函数利用不同类型的核函数之间的优势互补，可以达到更好的效果。本文构造复合核权重矩阵的过程可分为以下流程：

1) RBF核函数改造

本文继续选用经典而常用的RBF核函数，不仅考虑到其良好的非线性映射性能，可以处理非线性可分情况，还因为该核函数也是欧氏距离的一种表示，体现了样本在特征空间里光谱亮度差异。

本文在RBF核函数的基础上进行一定的改进，得到了一种组合核函数。其具体实现为：

①采用近邻法构建有标记样本和无标记样本的近邻关系图。若与为近邻，则在近邻关系矩阵中有边连接，否则无边连接；

②设置近邻关系矩阵中边的权值矩阵=[]，表达式如下：

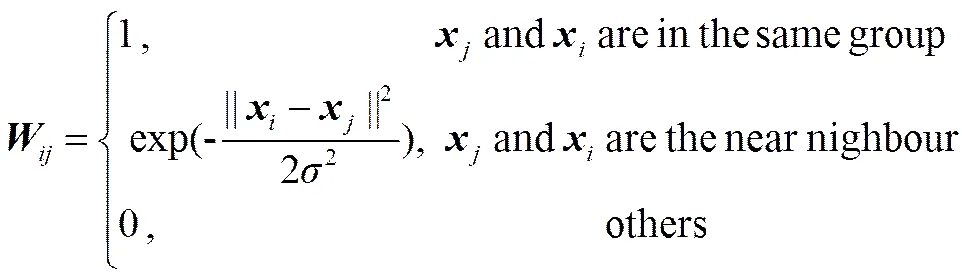
2) 构造光谱角核函数权重矩阵

光谱角(SAM)是以运算影像像元的光谱与样本参考光谱之间的夹角来区分类别。其原理是把像元的光谱(多个波段的像素值)作为矢量投影到维空间上，各光谱曲线被看作有方向且有长度的矢量，而光谱之间形成的夹角叫光谱角，光谱角分类法是依据光谱角的大小来进行分类的，而没有考虑光谱矢量的长度( 影像的亮度)。光谱角的数学表达式为

其中：θ为影像像元光谱与参考光谱之间的夹角，为影像像元光谱曲线矢量，为参考光谱曲线矢量。光谱角以很小的弧度角θ来表示，它代表了光谱曲线之间大部分的光谱相似性。

本文构造光谱角核函数权重矩阵的方法为

①计算两两样本点之间的光谱角θ，具体方法参照式(7)，得到一个光谱角信息的矩阵；

②设置近邻关系矩阵中边的权值矩阵=[]，表达式如下：

3) 构造复合核权重矩阵

至此，已得出本算法所用的两个基核分别构造的近邻矩阵：RBF核近邻矩阵和光谱角核近邻矩阵，将和加权构造复合核近邻矩阵，在此复合权重矩阵的基础上进行聚类：

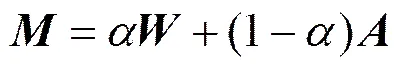
3 实验与分析

3.1 实验设置

在实验中，选用两个高光谱遥感数据集，即Indian Pine和Botswana数据集，每类地物中分别随机标记5，10，... 50，55个点，每次实验重复运行10次，最终取分类精度的平均值。为尽可能减小环境因素对实验结果的影响，每次实验均将多种方法在同一数据集选取的相同样本点上依次进行。实验中对比的算法有K-means算法，FCM算法，SSGC算法(其参数设置为：式(1)中的RBF核宽度置为0.01，式(3)中用到的置为0.99)。最后，本文提出的SSGCK算法参数设置为：近邻点数设置为5。

由于本方法中用到了两个权重矩阵，两者的权重分配可能会影响分类正确率。本文通过调整子核函数权值，得到与分类正确率的关系图，如图1所示。

图 1 RBF 核权值系数对SSGCK 算法分类正确率的影响

由图1可以看出，改变系数会对实验结果产生一定的影响，且为0.8~0.9时，分类效果最为理想。本文所用算法中将值设定为0.85。

3.2 Indian Pine 数据集

为了验证本文算法的有效性，在仿真数据中首先采用目前国内外广泛采用的印第安纳（Indian Pine）高光谱遥感数据集进行测试实验，其假彩色图像如图2所示。该数据集的大小为145×145，共有220个波段以及17类已知地物类别。去除水汽吸收明显和低信噪比波段后，剩余200个波段用于实验，并从数据点较多的地物类别中随机选择6类进行实验。

图2 印第安纳高光谱遥感影像

图3显示了不同方法在印第安纳数据集上分类结果，其中图3(a)为几种方法分类正确率与标记点数的关系，为了对比单核算法与复合核算法的效果，实验中也加入了SSGCK(=0)与SSGCK(=1)两种单核算法；图3(b)是几种方法运行时间对比。

由图3(a)可以看出，增加标记点数，SSGC和SSGCK方法分类正确率都稳步提升，且SSGCK方法正确率一直高于SSGC方法。同时复合核的SSGCK算法正确率优于单纯的RBF核算法(对应于图3中SSGCK(=1))和光谱角核算法(对应图3中SSGCK(=0))。较之于传统的FCM聚类算法、K-means算法，SSGCK算法正确率有大幅提升。

由图3(b)中数据可以看出，本文提出的SSGCK算法在运行时间上处于中等水平，相对于传统方法没有优势，但相对于原来的SSGC方法，时间大大缩短，改善效果显著。

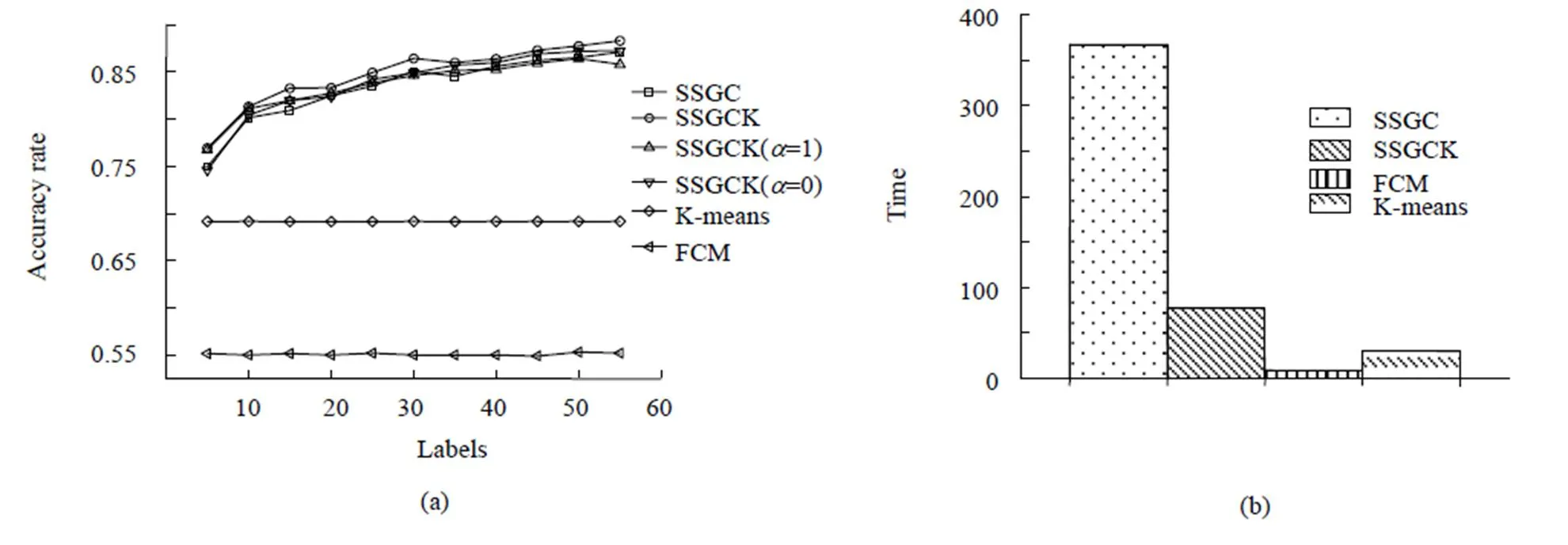
图3 不同方法在印第安纳数据集上分类结果(a) 不同方法的整体分类精度；(b) 不同方法的运行时间

(a) The overall classification accuracy of different algorithms; (b) Running time of different algorithms.

图4是使用四种方法对印第安纳影像进行分类的结果。

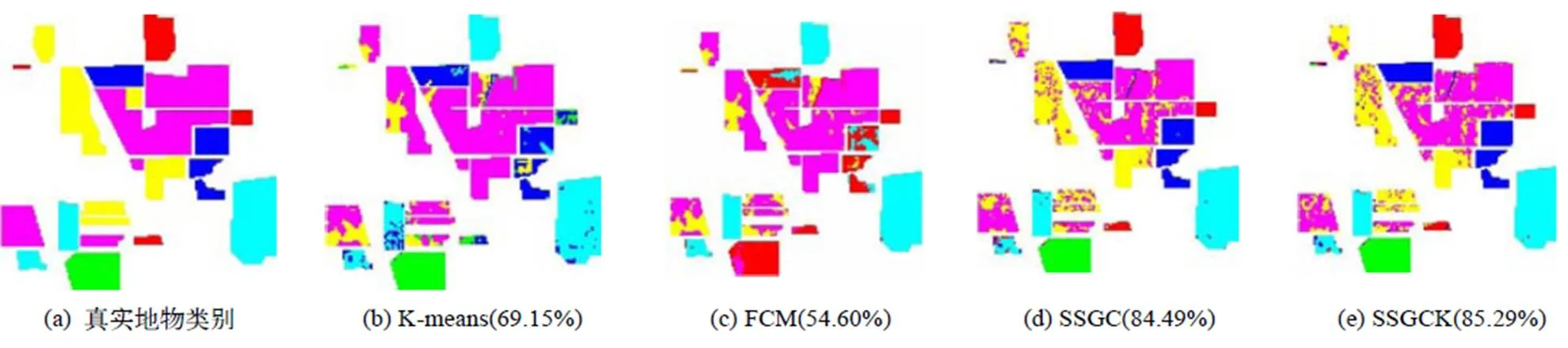
图4 不同方法在印第安纳数据集上分类结果对应的假彩色图

以上实验结果显示，K-means，FCM算法分类结果较差，较多地物被误分，主要原因是这两种算法忽略了数据的全局结构，损失了较多信息。基于RBF核的SSGC算法在精度上优于K-means和FCM算法。而本文提出的半监督复合核图聚类算法将RBF核与光谱角核融合，取得的效果明显优于基于单一RBF核聚类方法，这是多核相对于单核的优势，单个核函数构成的核机器并不能应对诸如数据异构或不规则、样本规模巨大、样本不平坦分布等实际问题，而多核分类却能应对自如。

3.3 Botswana数据集

Botswana高光谱遥感影像数据集于2001年5月31日由美国宇航局通过EO-1卫星上高光谱传感器获得，该影像由1 476´256个像素组成，包括波长为400 nm~2 500 nm共有242个波段，空间分辨力达到30 m，光谱分辨力达到10 nm，覆盖了博茨瓦纳奥卡万戈三角洲地区长7.7 km的带状地带，去除受大气吸收和噪声影响的波段，将剩下的145个(10~55，82~97，102~119，134~164，187~220)波段用于实验研究。图5为Botswana高光谱遥感影像的假彩色图及其真实地物分布情况。

图5 Botswana 高光谱遥感影像

图6(a)显示实验中所用4种方法在Botswana数据集上分类正确率与标记点数的关系，图6(b)显示在此数据集上不同方法运算时间对比。

由图6(a)可见，增加标记点数，半监督算法的准确率均逐步提升，显示了半监督方法对于先验知识的利用效果。同时SSGC算法与SSGCK算法准确率遥遥领先于传统算法，因为二者都用到了RBF核函数，RBF核能够进行非线性变换，将样本在一个维度更高的特征子空间中处理，足以应对复杂数据。而本文提出的SSGCK算法正确率一直优于SSGC算法，可提升1%~4%，能更好地应对数据异构等问题。

图6(b)中，SSGCK算法相对于SSGC算法，实验运行时间大大缩短。原因是本文对RBF核函数进行了改造，删除了不必要的计算环节，而这些环节也是非常耗时的。

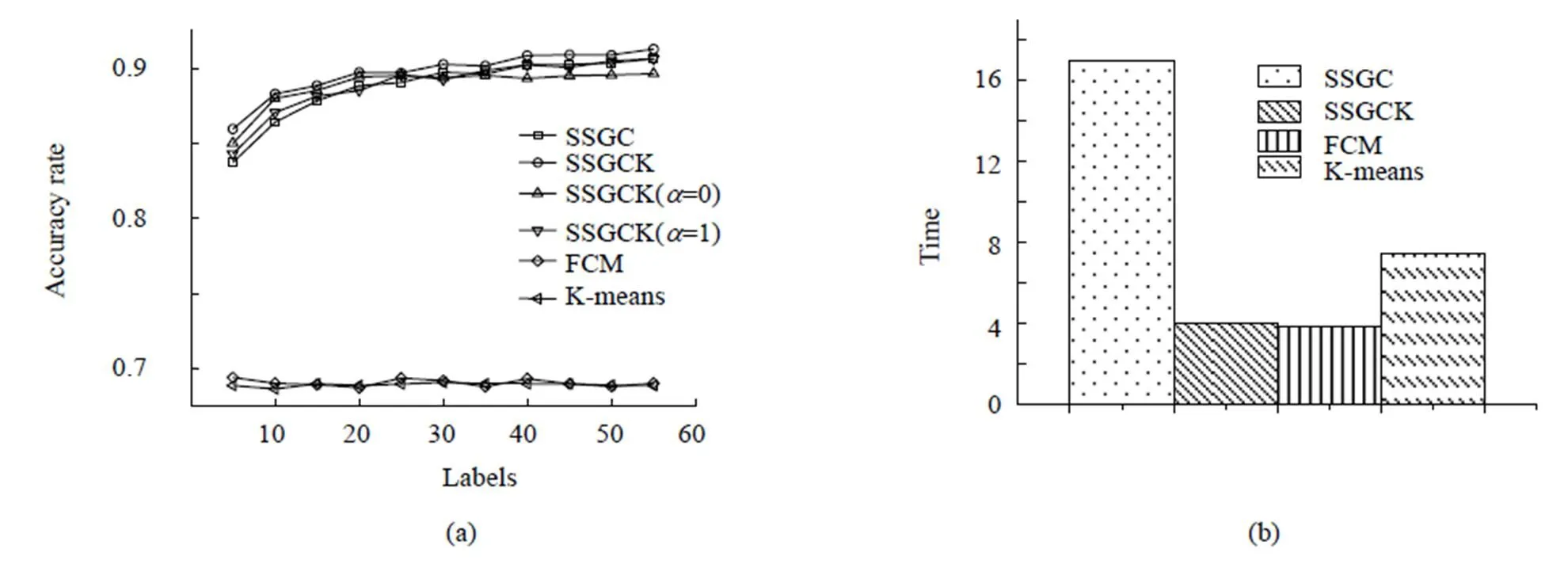
图6 不同方法在Botswana 遥感影像上分类结果

(a) 不同算法的整体分类精度；(b) 不同方法的运行时间

Fig.6 Botswana hyperspectral data classification results by different methods

(a) The overall classification accuracy of different algorithms；(b) Running time of different algorithms

4 结 语

本文提出了一种半监督复合核图聚类算法，该方法在构造近邻矩阵时，使用本文构造的组合核函数，取代原有的RBF核函数，实现对先验信息的高效利用；同时为突破单核函数的局限，本文又结合光谱角核函数，构造出复合核权重矩阵；最后又将K近邻方法引入近邻矩阵的构造过程，在没有引入Nyström方法的情况下大大提升了运算速度。实验结果验证了本文算法的有效性：在Indian Pine和Botswana数据集上分类结果显示，相对于传统K-means，FCM算法，准确率提升10%~20%，相对于SSGC算法，可以提升1%~4%；且相对于SSGC算法，分类时间下降显著。

在实验中还有一些方面值得研究，比如本文中用到的参数是单核聚类情况下的最优值，其在复合核函数中可能不是最优的，故参数优化问题仍有研究价值。

[1] 李吉明，贾森，彭艳斌. 基于光谱特征和纹理特征协同学习的高光谱图像数据分类 [J]. 光电工程，2012，39(11)：88-94.

LI Jiming，JIA Sen，PENG Yanbin. Hyperspectral data classification with spectral and texture features by co-training algorithm [J]. Opto-Electronic Engineering，2012，39(11)：88-94.

[2] 赵春晖，齐滨. 基于模糊核加权C-均值聚类的高光谱图像分类 [J]. 仪器仪表学报，2012，33(9)：2016-2021.

ZHAO Chunhui，QI Bin. Hyperspectral image classification based on fuzzy kernel weighted c-means clustering [J]. Chinese Journal of Scientific Instrument，2012，33(9)：2016-2021.

[3] 李巧兰. 基于约束的半监督聚类的图像分割算法研究 [D]. 西安：西安电子科技大学，2014：1-2.

LI Qiaolan. Semi-supervised clustering based on constraints for image segmentation [D]. Xi¢an：Xidian University，2014：1-2.

[4] 冷明伟. 主动半监督聚类及其在社团检测中的应用研究 [D]. 兰州：兰州大学，2014：14-23.

LENG Mingwei. Research of active semi-supervised clustering and its application in community detection [D]. Lanzhou：Lanzhou University，2014：14-23.

[5] 陈小冬，尹学松，林焕祥. 基于判别分析的半监督聚类方法 [J]. 计算机工程与应用，2010，46(6)：139-143.

CHEN Xiaodong，YIN Xuesong，LIN Huanxiang. Semi-supervised clustering approach with discriminant analysis [J]. Computer Engineering and Applications，2010，46(6)：139-143.

[6] Camps-Valls Gustavo，Marsheva Tatyana V. Bandos，ZHOU Dengyong. Semi-supervised graph-based hyperspectral image classification [J]. IEEE Transactions on Geoscience and Remote Sensing(S0196-2892)，2007，45(10)：3044-3054.

[7] 李亚娥. 基于图的半监督分类算法研究 [D]. 西安：陕西师范大学，2012：15-18.

LI Ya¢e. Research on graph-based semi-supervised classification algorithm [D]. Xi'an：Shanxi Normal University，2012：15-18.

[8] Papadopoulos Dimitris F，Simos Theodore E.A modified runge-kutta-nyström method by using phase lag properties for the numerical solution of orbital problems [J]. Applied Mathematics & Information Sciences(S1935-0090)，2013，7(2)：433-437.

[9] 谢娟英，郭文娟，谢维信，等. 基于样本空间分布密度的初始聚类中心优化K-均值算法 [J]. 计算机应用研究，2012，29(3)：888-892.

XIE Juanying，GUO Wenjuan，XIE Weixin，. K-means clustering algorithm based on optimal initial centers related to pattern distribution of samples in space [J]. Applications Research of Computers，2012，29(3)：888-892.

[10] 王峰，籍锦程，聂百胜. K-均值聚类模糊逻辑数据融合改进算法研究 [J]. 中北大学学报：自然科学版，2014，35(6)：699-703.

WANG Feng，JI Jincheng，NIE Baisheng. An improved fusion method of fuzzy logic based on k-mean clustering [J]. Journal of North University of China：Natural Science Edition，2014，35(6)：699-703.

[11] 张慧哲，王坚. 基于初始聚类中心选取的改进FCM聚类算法 [J]. 计算机科学，2009，36(6)：206-209.

ZHANG Huizhe，WANG Jian. Improved fuzzy c-means clustering algorithm based on selecting initial clustering centers [J]. Computer Science，2009，36(6)：206-209.

[12] Kannan S R，Ramathilagam S. Effective fuzzy c-means clustering algorithms for data clustering problems [J]. Expert Systems with Applications(S0957-4174)，2012，39(7)：6292–6300.

[13] ZHAO Weizhong，HE Qing，MA Huifang. Effective semi-supervised document clustering via active learning with instance-level constraints [J]. Knowledge & Information Systems(S0219-1377)，2012，30(3)：569-587.

[14] Ozer Sedat，CHEN Chi H. A set of new chebyshev kernel function for support vector machine pattern classification [J]. Pattern Recognition(S0031-3203)，2011，44(7)：1435-1447.

[15] ZHANG Rui，WANG Wenjian. Facilitating the application of support vector machine by using a new kernel [J]. Export Systems with Applications(S0957-4174)，2011，38(11)：14225-14230.

Semi-supervised Graph Clustering with Composite Kernel and Its Application in Hyperspectral Image

LI Zhimin，HAO Panchao，HUANG Hong，HUANG Wen

( Key Laboratory of Optoelectronic Technology and Systems of the Education Ministry of China, Chongqing University, Chongqing 400030, China )

A semi-supervised graph-based clustering method is presented with composite kernel for the hyperspectral images, mainly to solve the problems existed in an algorithm called Semi-Supervised Graph-Based Clustering (SSGC) and improve its performance. As for the realization, it firstly reforms the Radial Basis Function (RBF) by adopting semi-supervised approach, to exploit the wealth of unlabeled samples in the image. Then, it incorporates the spectral angle kernel with RBF kernel, and constructs a composite kernel. At last, the use of K-Nearest Neighbor (NN) method while constructing the weight matrix has greatly simplified the calculation. Experimental result in Indian Pine and Botswana hyperspectral data demonstrates that this algorithm can not only get higher classification accuracy (1%~4% higher than SSGC, 10%~20% higher than K-means and Fuzzy C-Means (FCM), but effectively improve operation speed compared with SSGC.

hyperspectral remote sensing image; clustering; semi-supervised learning; composite kernel

TP391；TP751

A

10.3969/j.issn.1003-501X.2016.04.006

2015-05-31；

2015-08-25

国家自然科学基金(61101168)；重庆市基础与前沿研究计划(cstc2013jcyjA40005)

李志敏(1955-)，男(汉族)，重庆人。副教授，硕士生导师，主要研究方向为数字图像处理、计算机网络、嵌入式系统。

E-mail: lzm@cqu.edu.cn。