基于压缩感知的加速前向后向匹配追踪算法

王 锋 孙桂玲 张健平 何静飞



基于压缩感知的加速前向后向匹配追踪算法

王 锋①孙桂玲*①张健平②何静飞①

① (南开大学电子信息与光学工程学院 天津 300350)②(上海交通大学电子信息与电气工程学院 上海 200030)

前向后向匹配追踪(FBP)算法作为一个新颖的两阶段贪婪逼近算法，因为较高的重构精度和不需要稀疏度作为先验信息的特点，受到了人们的广泛关注。然而，FBP算法必须运行更多的时间才能得到更高的精度。鉴于此，该文提出加速前向后向匹配追踪(AFBP)算法。该算法利用每次迭代中候选支撑集的信息，实现对已删除原子的再次加入，以此减少算法迭代次数。通过不同非零项分布的稀疏信号和稀疏图像的仿真结果表明，相对于FBP算法，该文提出的方案在不降低重构精度的同时，大幅降低了算法运行时间。

压缩感知；贪婪算法；前向后向搜索；稀疏信号重构

1 引言

压缩感知(Compressed Sensing, CS)[1, 2]将稀疏信号的采样和压缩进行结合，从而降低测量系统的采样率和计算复杂度。这一特性使得压缩感知在无线传感器网络[3]、核磁共振成像等领域[4, 5]有广泛应用前景。压缩感知重构算法可以分为3大类：贪婪算法，凸松弛算法和贝叶斯框架。其中，贪婪算法因为有较快的速度和简单的框架而被广泛应用。贪婪算法主要包括匹配追踪(MP)算法[6]，正交匹配追踪(OMP)算法[7]，分段正交匹配追踪(StOMP)算法[8]，子空间追踪(SP)算法[9]，压缩采样匹配追踪(CoSaMP)算法[10]，稀疏度自适应匹配追踪(SAMP)算法[11]，前向预测正交匹配追踪(LAOMP)算法[12]和前向后向匹配追踪(Forward-Backward Pursuit, FBP)算法[13]。为了进一步提高算法性能，许多迭代[14]和融合的改进策略被应用于这些贪婪算法。

由于OMP算法没有回溯机制，而SP算法又需要稀疏度作为先验信息，文献[13]提出了FBP算法。在FBP算法中，每一步迭代主要包含两个阶段：前向阶段和后向阶段。前向阶段通过前向步长扩大估计支撑集，后向阶段通过后向步长减小估计支撑集。本文提出的加速前向后向匹配追踪(Acceleration Forward-Backward Pursuit, AFBP)算法，克服了FBP算法每次迭代只能以固定步长扩大支撑集、忽视被删除原子质量的缺点，利用前向阶段支撑集中原子的信息，对后向阶段被删除原子进行再此选入，达到自适应地决定每次迭代所增加原子数目的目的。虽然文献[13]指出通过调节参数，可以降低FBP算法运行时间，但会导致重构精度的下降。而本文提出的加速策略则有效解决这一矛盾。

本文在第2节介绍了压缩感知模型与FBP重构算法；第3节首先提出加速策略，然后描述 AFBP算法的具体流程；第4节为性能比较试验，通过对1维稀疏信号和2维图像下 AFBP 算法与 FBP 算法的仿真结果进行分析比较，说明改进算法的有效性；第5节对该加速策略进行总结。

2 压缩感知和重构算法

2.1压缩感知理论

标准压缩感知测量过程可表示成式(1)形式：

2.2 传统的前向后向匹配追踪算法

FBP算法是一个两阶段迭代算法。该算法在不知道稀疏度的情况下，通过迭代以固定步长逐步扩大估计支撑集，最后实现对稀疏信号的逼近。表1给出了FBP算法的伪代码。

表1 FBP算法

3 加速前向后向匹配追踪算法

3.1加速策略

FBP算法对原子的操作主要集中在两个阶段：第一，利用相关性将原子选入支撑集；第二，依据投影系数将原子移除支撑集。本文算法在移除原子后，并不直接进入下一迭代，而是参考被移除原子在之前迭代过程中与残差的相关性情况，从而进一步判断该原子是否具有再次加入支撑集的资格。基于此，本文提出的算法可以实现每次迭代自适应地改变选入估计支撑集的原子个数，克服FBP算法每次迭代只能以固定步长增加估计支撑集的弊端。如果在历次迭代中，某原子与历次残差的相关程度一直很高，则该原子为正确原子的概率就会很大。此时如果仅仅依据删除阶段的投影系数大小来决定原子是否应保留在支撑集，则会延缓算法的运行，甚至导致算法迭代失败。然而，如果开辟一条选择原子的新渠道，及时将此原子加入支撑集，则会加速算法的运行。

3.2 加速前向后向匹配追踪算法

表2 AFBP算法

4 实验结果及分析

4.1 1维稀疏信号重构

为了展示加速策略的优势，本文参照文献[13]，从准确重构概率，平均重构误差和运行时间3方面对AFBP算法和FBP算法进行比较。测试信号的非零项分别服从高斯，均匀和常数幅度随机符号(Constant Amplitude Random Sign, CARS)分布。其中，高斯稀疏信号非零项来自标准高斯分布。均匀稀疏信号非零项为之间的均匀分布。CARS稀疏信号非零项由单位幅度随机符号的元素组成。在实验中，每一稀疏信号均对应一个不同的观测矩阵。其中观测矩阵的元素服从均值为0，标准差为1/的高斯分布，且每一列均进行归一化处理。为比较AFBP和FBP的运行时间，本文采用文献[14]的设定。即通过MATLAB自带的‘cputime’函数计算平均运行时间。为避免MATLAB采用多线程计算，本文使用MATLAB中‘singleCompThread’的选项。该选项将限制MATLAB使用单线程工作。以下为运行仿真的计算机信息。Matlab 版本：R2010b (32-bit)，操作系统：Windows (32-bit)，处理器：Intel(R) Core(TM) i5-3210M CPU @ 2.50 GHz，内存：4 GB。

图 1 高斯稀疏信号的重构结果比较()

图2 均匀稀疏信号的重构结果比较()

图3 CARS稀疏信号的重构结果比较()

图4 高斯稀疏信号的重构结果比较()

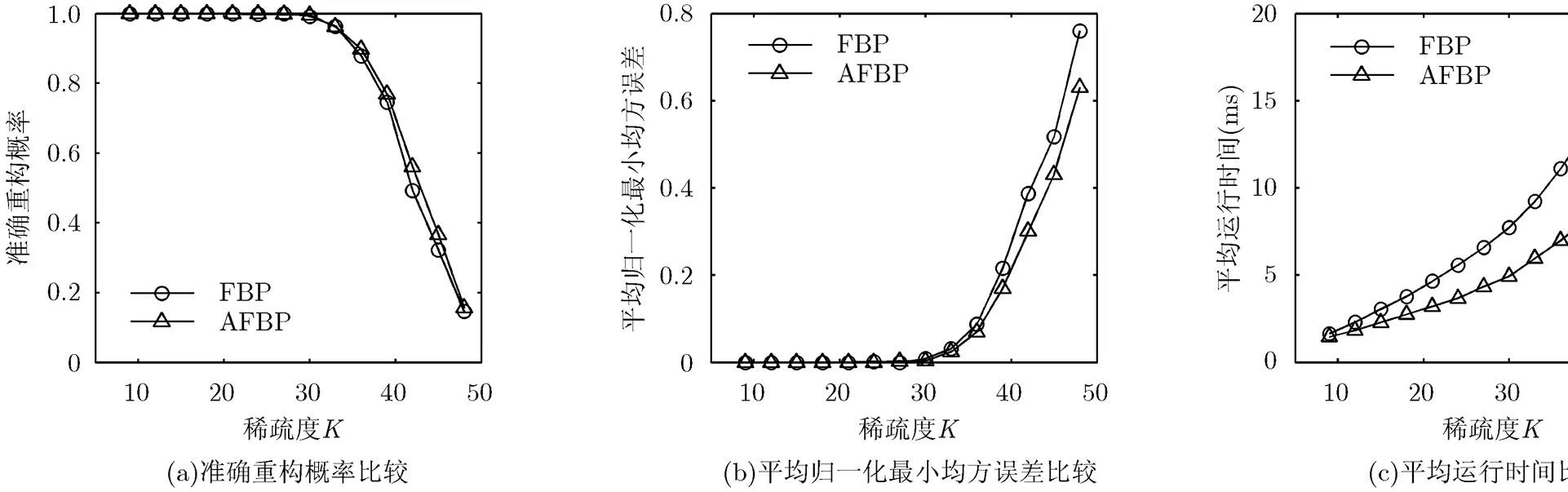
图5 均匀稀疏信号的重构结果比较()

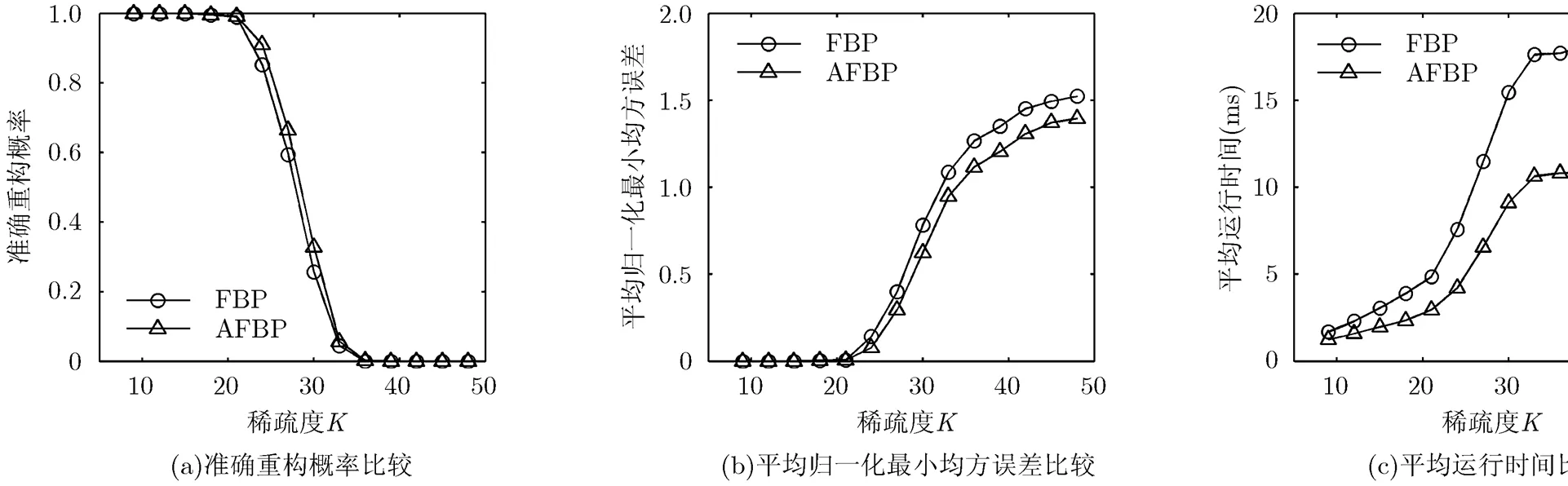
图6 CARS稀疏信号的重构结果比较()

4.2参数选择

图7给出了高斯稀疏信号下，不同参数AFBP算法的性能比较。其中AFBP和FBP的步长参数均为。AFBP前两类参数与上面实验设定一致，而第3类参数设定如下：AFBP1,,,; AFBP2,,,; AFBP3,,,。由图7可知，对于准确重构概率，AFBP算法和FBP算法均高于OMP, SP和BP。AFBP算法准确重构概率基本随阈值增大而提升。其中，AFBP1准确重构概率在稀疏度比较大时，略低于FBP。而AFBP2和AFBP3准确重构概率一直优于FBP。对于平均归一化最小均方误差，不同参数AFBP均优于FBP, OMP和SP。其中，不同参数AFBP虽性能差距不明显，但依然是AFBP3最优，AFBP1最差。BP仅是在稀疏度较大时优于AFBP。其他情况下，AFBP算法均优于其他算法。对于平均运行时间，不同参数AFBP均优于FBP。而随着阈值降低，AFBP运行时间也相应变短。其中，AFBP1的运行时间基本与OMP和SP相当。由于BP算法运行时间过长，所以并未在图中列出。

图7 不同参数AFBP在高斯稀疏信号下的重构结果比较()

为保证AFBP算法准确重构概率和均方误差均不低于FBP算法，本文推荐AFBP2的阈值参数，即阈值参数基本为左右，且。其它分布信号的参数规律与此情况类似，由于篇幅有限，不再赘述。

为进一步分析所提出加速策略，本文在图8中展示了经加速渠道选入支撑集的原子的具体信息。由图8可知，阈值越低，经加速渠道选入原子越多。虽然随着阈值降低，经加速渠道选入的正确原子有所增加，但原子正确率却有一定程度降低。此外，随着稀疏度增加，经加速渠道选入的原子增多。可见，随着稀疏度增大，加速效果愈加明显。但是正确原子的数目却在稀疏度超过39之后有所下降。由图8(c)可知，经加速渠道选入原子的正确率在稀疏度大于30后开始下降。此稀疏度恰为FBP算法开始失败的稀疏度。可见，加速策略性能与FBP算法性能紧密相关。虽然，稀疏度超过30后，加速策略正确率开始降低，但是由图7可知，AFBP依然优于FBP。这是由于此时FBP算法准确率也在降低，所以总体上如果参数选择恰当AFBP依然可以优于FBP。值得注意的是，对于AFBP1，虽然在稀疏度较低时经加速渠道选入原子的正确率偏低，但是并不影响算法的整体性能。这是因为AFBP算法继承了FBP算法在稀疏度较低时的强大纠错能力。由图8可知，虽然AFBP1加速效果明显，但是经加速渠道选入原子的正确率一直低于AFBP2和AFBP3。而AFBP3又用时过长，故推荐AFBP2的阈值参数。

图8 不同参数AFBP在高斯稀疏信号下经加速渠道选入原子的具体信息比较()

4.32维图像重构

为验证AFBP对实际非零系数分布信号的重构性能，本文使用256×256的图像‘Lena’进行实验。实验参数与文献[13]类似。为将恢复问题分解一系列简单子问题，本文首先把图像分割为8 × 8的小块。分割处理保证每个8×8小块在2D的Haar小波基上是稀疏的，其中为12。即每个分块仅保留12个最大幅度的小波系数。对于每一分块，信号长度为64，测量值设定为32。观测矩阵从均值为0标准差为1/的高斯分布中随机得到，并归一化每一列。,。AFBP与FBP的前向和后向步长均设置为：,。AFBP其他参数设置如下，，其中阈值参数遵循大小为左右且的原则。

图9 各算法对图像“Lena”的重构效果

5 结论

本文提出了基于压缩感知的加速前向后向匹配追踪重构算法，即AFBP算法。AFBP算法继承FBP算法不需要稀疏度作为先验信息的优点，同时引入分段思想和加速策略。在前向阶段，AFBP算法利用不同权重记录估计支撑集中新加入原子的相关性信息。在后向删除阶段，通过比较被淘汰原子的权重和相应的预设阈值，AFBP算法建立了一条原子加入估计支撑集的新渠道。前向阶段的相关性权重累加和后向阶段的阈值比较，确保了经该渠道加入估计支撑集的原子的准确性，从而达到在保证精度的同时加快算法运行速度目的。

参考文献

[1] Donoho D L. Compressed sensing[J]., 2006, 52 (4): 1289-1306.doi: 10.1109/TIT.2006.871582.

[2] Candès E J, Romberg J, and Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]., 2006, 52(2): 489-509. doi: 10.1109/TIT.2005.862083.

[3] 李鹏,王建新,曹建农. 无线传感器网络中基于压缩感知和GM(1,1)的异常检测方案[J]. 电子与信息学报, 2015, 37(7): 1586-1590. doi: 10.11999/JEIT141219.

LI Peng, WANG Jianxin, and CAO Jiannong. Abnormal event detection scheme based on compressive sensing and GM (1,1) in wireless sensor networks[J].&, 2015, 37(7): 1586-1590. doi: 10.11999/JEIT141219.

[4] 蒋明峰, 刘渊, 徐文龙, 等. 基于全变分扩展方法的压缩感知磁共振成像算法研究[J]. 电子与信息学报, 2015, 37(11): 2608-2612. doi:10.11999/JEIT150179.

JIANG Mingfeng, LIU Yuan, XU Wenlong,. The study of compressed sensing MR image reconstruction algorithm based on the extension of total variation method[J].&, 2015, 37(11): 2608-2612. doi:10.11999/JEIT150179.

[5] QU X, HOU Y, FAN L,. Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator[J]., 2014, 18(6): 843-856. doi:10.1016/j.media.2013.09.007.

[6] Mallat S G and ZHANG Z. Matching pursuits with time-frequency dictionaries[J]., 1994, 41(12): 3397-3415. doi:10.1109/78.258082.

[7] Tropp J and Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J].2007, 53(12): 4655-4666. doi:10.1109/TIT.2007.909108.

[8] Donoho D L, Tsaig Y, Drori I,. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J].2012,58(2): 1094-1121. doi:10.1109/ TIT.2011.2173241.

[9] DAI W and Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J].2009, 55(5): 2230-2249. doi:10.1109/TIT.2009.2016006.

[10] Needell D and Tropp J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]., 2009, 26(3): 301-321. doi:10.1016/j.acha.2008.07.002.

[11] Do T T, Gan L, Nguyen N,. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]. 42nd IEEE Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, 2008: 581-587. doi:10.1109/ACSSC.2008.5074472.

[12] Chatterjee S, Sundman D, and Skoglund M. Look ahead orthogonal matching pursuit[C]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 2011: 4024-4027. doi:10.1109/ICASSP.2011.5947235.

[13] Karahanoglu N B and Erdogan H. Compressed sensing signal recovery via forward-backward pursuit[J]., 2013, 23(5): 1539-1548. doi:10.1016/j.dsp.2013.05.007.

[14] Ambat S K and Hari K V S. An iterative framework for sparse signal reconstruction algorithms[J]., 2015, 108: 351-364. doi:10.1016/j.sigpro.2014.09.023.

[15] Ambat S K, Chatterjee S, and Hari K V S. Progressive fusion of reconstruction algorithms for low latency applications in compressed sensing[J]., 2014, 97(7): 146-151. doi:10.1016/j.sigpro.2013. 10.019.

[16] Ambat S K, Chatterjee S, and Hari K V S. A committee machine approach for compressed sensing signal reconstruction[J]., 2014, 62(7): 1705-1717. doi:10.1109/TSP.2014.2303941.

[17] Deepa K G, Ambat S K, and Hari K V S. Modified greedy pursuits for improving sparse recovery[C]. Twentieth IEEENational Conference on Communications (NCC), Kanpur, 2014: 1-5. doi:10.1109/NCC.2014.6811370.

Acceleration Forward-backward Pursuit Algorithm Based on Compressed Sensing

WANG Feng①SUN Guiling①ZHANG Jianping②HE Jingfei①

① (,,300350,)②(,,200030,)

The Forward-Backward Pursuit (FBP) algorithm, a novel two stage greedy approach, receives wide attention due to the high reconstruction accuracy and the feature without prior information of the sparsity. However, FBP has to run more time to get a higher precision. To alleviate this drawback, this paper proposes the Acceleration Forward-Backward Pursuit (AFBP) algorithm based on Compressed Sensing (CS). In order to reduce the number of iterations, the algorithm exploits the information available in the support estimate to add the deleted atoms again. The run time of AFBP is sharply shorter than that of FBP, while the precision of AFBP is not lower than FBP. The efficacy of the proposed scheme is demonstrated by simulations using random sparse signals with different nonzero coefficient distributions and a sparse image.

Compressed Sensing (CS); Greedy algorithms; Forward-backward search; Sparse signal reconstruction

TN911.72

A

1009-5896(2016)10-2538-08

10.11999/JEIT151422

2015-12-14；改回日期：2016-05-05；网络出版：2016-07-04

孙桂玲sungl@nankai.edu.cn

国家自然科学基金(61171140)，高等学校博士学科点专项科研基金(20130031110032)

The National Natural Science Foundation of China (61171140), The Doctoral Program of Higher Education (20130031110032)

王 锋： 男，1990年生，博士生，研究方向为压缩感知、无线传感器网络等.

孙桂玲： 女，1964年生，教授，研究方向为压缩感知、无线传感器网络、信号与信息处理、信息检测与智能控制系统等.

张健平： 男，1996年生，本科生，研究方向为无线通信.