基于规范变换的前向神经网络的洪水灾害评估模型

徐源蔚， 李祚泳， 汪嘉杨

(成都信息工程大学资源环境学院，四川成都610225)

自然灾害种类众多，其中洪水灾害是全球更是中国影响范围广、损害最严重的自然灾害之一［1］。因而对洪水灾害所造成的生命、财产损失进行客观、有效的评估能为减灾、防灾决策提供依据，对有关管理部门制定科学的减灾、救灾决策具有一定的参考价值。

国内、外对灾害指标的选择及灾情评估模型和方法已有很多研究［2-6］。主要有模糊综合评价法［7］、灰色聚类评价法［8］、物元可拓评价法［9-10］、集对分析评价法［11］等不确定性评价法和人工神经网络［12］、投影寻踪［13］、支持向量机［14］等智能评价模型。不确定性分析评价法虽然考虑了灾情指标所具有的模糊性、灰色性、不相容性、既确定又不确定等特性，但当指标较多时，评价函数的设计和计算工作量大，且评价函数的设计有较大的主观性。人工智能评价模型能很好的适用于非线性、非正态、高维数据处理，但模型中有较多的参数需要优化确定。其中最常用的BP神经网络虽然具有自学习、自适应和较强的非线性映射能力及原理简单等优点，但也存在学习效率低、收敛速度慢和易于陷入局部极值的缺陷。而用优化算法直接优化网络连接权值的前向神经网络(forward neural network，FNN)(简称前向网络)虽然能较好地避免陷入局部极值，但需要优化的网络参数也较多。智能评价模型的共同局限是模型的编程和计算都较复杂，实际使用不便;当指标较多时，还影响模型的优化效率和求解精度，更不能建立对不同评价指标或不同指标数目都能普适、通用的前向网络模型，因而包括前向网络模型在内的智能评价模型应用于指标较多的灾情评估亦受到很大的限制。

但若对灾情各指标值进行规范变换，使规范变换后的不同指标的同级标准规范值之间差异较小，从而规范变换后的各指标可视作“等效”于同一个规范指标，因而只需构建对任意指标规范值都适用的2个指标的2-2-1和3个指标的3-2-1两种简单结构的前向网络模型;而对灾害指标多于3个以上的的前向网络建模，可以通过将多指标的前向网络模型分解为以上两种简单结构的前向网络模型的组合表示即可。从而使灾情评估的前向网络建模不但更简化，而且适用范围也更广泛。在对洪水灾害指标值进行规范变换基础上，优化建立适用于指标规范值的2-2-1和3-2-1两种结构的前向神经网络模型输出表示式，并用于中国45个洪水灾情案例评估。

1 洪水灾害指标的参照值及指标值的规范变换式

具有一定代表性的中国部分省、市发生的洪水灾害所选用的灾害评价指标名称及分级标准cjk(j=1，2，3，4;k=1，2，3)如表1 所示［12］，其中，j代表指标，k 代表分级标准。可以看出，不同指标的同级标准值之间的单位、量纲和数值大小差异皆很大。不过，经观察、分析，若设置如表1所示的各指标参照值cj0、阈值cb和构造如式(1)和式(2)所示的各指标值的规范变换式，则经式(1)和式(2)规范变换后的不同指标的同级标准规范值x'jk差异变得较小，亦见表1。因而可以认为规范变换后的各指标皆“等效”于同一个规范指标，因而只需构建对各指标规范值都适用的2-2-1和3-2-1两种网络结构的洪水灾情评估前向网络模型即可。

式中，cj为指标j的实际值或分级标准值;cjb为设置的指标j的阈值;cj0为设置的指标j的参照值;xj和x'j分别为指标j的变换值和规范值。

表1 洪水灾害4项评估指标参照值cj0、分级标准值cjk、标准规范值x'jk及NV-FNN网络各级输出值

2 基于指标规范值的洪水灾害评价的前向神经网络模型

2．1 前向网络模型输出的一般表示式

由于具有非线性映射能力的双极性sigmoid函数的输出变化范围为0～1，可增大权值调整量，使前向网络的功能更强大，还能加速收敛。因此，为使建立的洪水灾害评价的前向网络既能保持较强的非线性映射能力，又使结构得到简化，采用双极性sigmoid函数作为前向网络隐层节点激活函数，而网络输出节点的输出则采用对隐节点输出的线性加权求和计算。其网络输出如式(3)所示。

式中，fh为用双极性sigmoid函数表示的隐节点h的输出;vhl为隐节点h与输出节点l的连接权值;H为隐层节点数目;Ol为输出节点l的输出。x为样本i的输入矢量，其中，x'ji为样本 i的指标 j的规范值;whj为输入节点j与隐节点h的连接权值;m为输入节点个数。

2．2 各级标准的指标规范值生成

为使建立的2-2-1结构和3-2-1结构的FNN模型具有较强的泛化能力(即推广能力)，除表1中各级标准的4项指标的标准规范值外，还在各级标准的此4项指标的标准规范值的均值方差变化范围内，再分别随机生成指标的96个标准规范值，使每级标准各有100个标准规范值，3级标准共有300个标准规范值。

2．3 构建2-2-1结构的前向网络模型

(1)生成训练样本

为构建2个输入节点和2个隐节点及1个输出节点的2-2-1结构的前向网络模型(FNN)，将上述生成的各级标准的100个标准规范值中的第1个和第2个指标规范值组成第1个训练样本的2个因子，第2个和第3个指标规范值组成第2个训练样本的2个因子，依次递推，…，第99个和第100个指标规范值组成第99个训练样本的2个因子，第100个和第1个指标规范值组成第100个训练样本的2个因子。每级标准有100个训练样本，3级标准共组成300个训练样本，用于训练2-2-1结构的前向网络的相邻两层节点之间的连接权值。

(2)前向网络2-2-1结构模型的输出表示式

设各级标准的训练样本的期望输出值和实际输出值分别为 Tl、Ol，(l=1，2，3)。则同级标准的100个训练样本的网络期望输出值 Tl(l=1，2，3)应设计为相同，3级标准的网络期望输出值Tl可分别设计为 T1=0.25，T2=0.30，T3=0.40。为优化网络节点之间的连接权值，需要设计优化目标函数式，如式(4)所示。

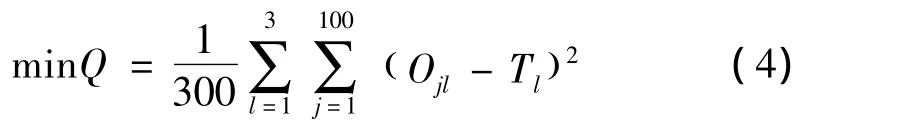
式中，Ojl为l级标准的训练样本j的网络实际输出值;Tl为l级标准的训练样本的期望输出值。

在满足优化目标函数式(4)条件下，用上述生成的300个训练样本代入式(3)所示的网络结构为2-2-1的前向网络，采用免疫进化的粒子群算法反复迭代优化，当优化目标函数式minQ≤8.24×10-4时，停止迭代，得到式(5)所示的结构为2-2-1的前向网络模型输出表示式。

2．4 构建3-2-1结构的前向网络模型

(1)生成训练样本

为构建3个输入节点和2个隐节点及1个输出节点的3-2-1结构的前向网络模型，类似网络结构为2-2-1的前向网络训练样本的组成，将上述生成的各级标准的100个标准规范值中的第1个、第2个和第3个指标规范值组成第1个训练样本的3个因子，第2个、第3个和第4个指标规范值组成第2个训练样本的3个因子，依次递推，……，第99个、第100个和第1个指标规范值组成第99个训练样本的3个因子，第100个、第1个和第2个指标规范值组成第100个训练样本的3个因子。每级标准仍是100个训练样本，3级标准共组成300个训练样本，用于训练3-2-1结构的前向网络的相邻两层节点之间的连接权值。

(2)前向网络3-2-1结构模型的输出表示式

同级标准的100个训练样本的网络期望输出值亦设置为与2-2-1网络结构的完全相同。设计优化目标函数式，如式(4)所示。在满足优化目标函数式(4)条件下，用上述生成的300个训练样本代入式(3)所示的网络结构为3-2-1的前向网络，亦采用免疫进化的粒子群算法反复迭代优化。当优化目标函数式minQ≤6.15×10-4时，停止训练，得到式(6)所示的结构为3-2-1的前向网络模型输出表示式。

3 模型效果检验

选取中国部分省市发生的45个洪水灾害的灾情案例对模型进行效果检验［15］。这些省市4项洪水灾害评估指标的分级标准值 cjk(j=1，2，…，4;k=1，2，3)及45个洪水灾害案例指标监测数据cji(j=1，2，…，4;i=1，2，…，45)分别如表1和表2所示。由表1所示的指标参照值cj0、cb和式(1)及式(2)计算出45个洪水灾害案例指标规范值x'ji，如表2所示。

依次将表1中各级标准的第1项和第2项指标，第2项和第3项指标，…，第4项和第1项指标的标准规范值组成样本的2项指标代入结构为2-2-1的前向网络模型输出式(5)。计算出4个2-2-1结构前向网络模型输出分级标准值，并求平均得2-2-1结构的模型输出实际分级标准值¯Ok(2-2-1)，如表1所示。

将表2中45个洪水灾害案例4项指标规范值按从小到大(或从大到小)排序，并将排序后的前2项、后2项指标规范值分别代入式(5)，计算得到各洪水灾害案例的2-2-1结构网络输出值、及其平均值O-i，如表2所示。依据表1网络输出分级标准值作出的洪水灾害评价结果，亦见表2。表2中还列出文献［15］用灰云聚类法、物元分析法和灾度判别评价结果。

对表2所列的分析结果进行统计，评估结果中，轻灾(Ⅰ类)的样本个数为22，中灾的(Ⅱ类)的样本个数为18，重灾(Ⅲ类)的样本个数为5。对比文献［15］中灰云聚类法、物元分析法和灾度判别评价结果，其中基于规范变换的前向神经网络与灰云聚类法、灾度判别法和物元分析法分别有38个、37个和33个洪水灾害案例评价结果相同，其符合度分别为84.4% 、82.2% 和73.3%。由此可得，基于规范变换的前向神经网络与灰云聚类法评价结果相符程度最高，与物元分析评价法相符程度较低。

4 结论

(1)对洪水灾害多于3个指标的前向网络建模，可将其分解为2-2-1和(或)3-2-1两种结构的前向网络模型的组合表示，故该模型不受指标多少限制，因而，该模型比BP神经网络模型或传统的前向网络模型适用范围更广。

(2)对任意洪水灾害个例，即使灾害指标与表1中的指标和分级标准并不相同，但只要能确定这些指标分级标准值，能适当设置出指标参照值cj0、阈值cb和指标值的规范变换式，使变换后的不同指标的同级标准规范值能在表1所示的各级标准规范值变化范围内或差异不大，则优化得出的前向网络模型输出式(5)和式(6)对该个例的指标也同样适用。

(3)用前向网络模型输出式(5)和式(6)对洪水灾害评估不用再编程计算，其评价过程比BP神经网络模型和传统的前向神经网络模型简单。

表2 中国部分省市45个洪水灾害案例监测值cj、规范值和多种方法评价结果

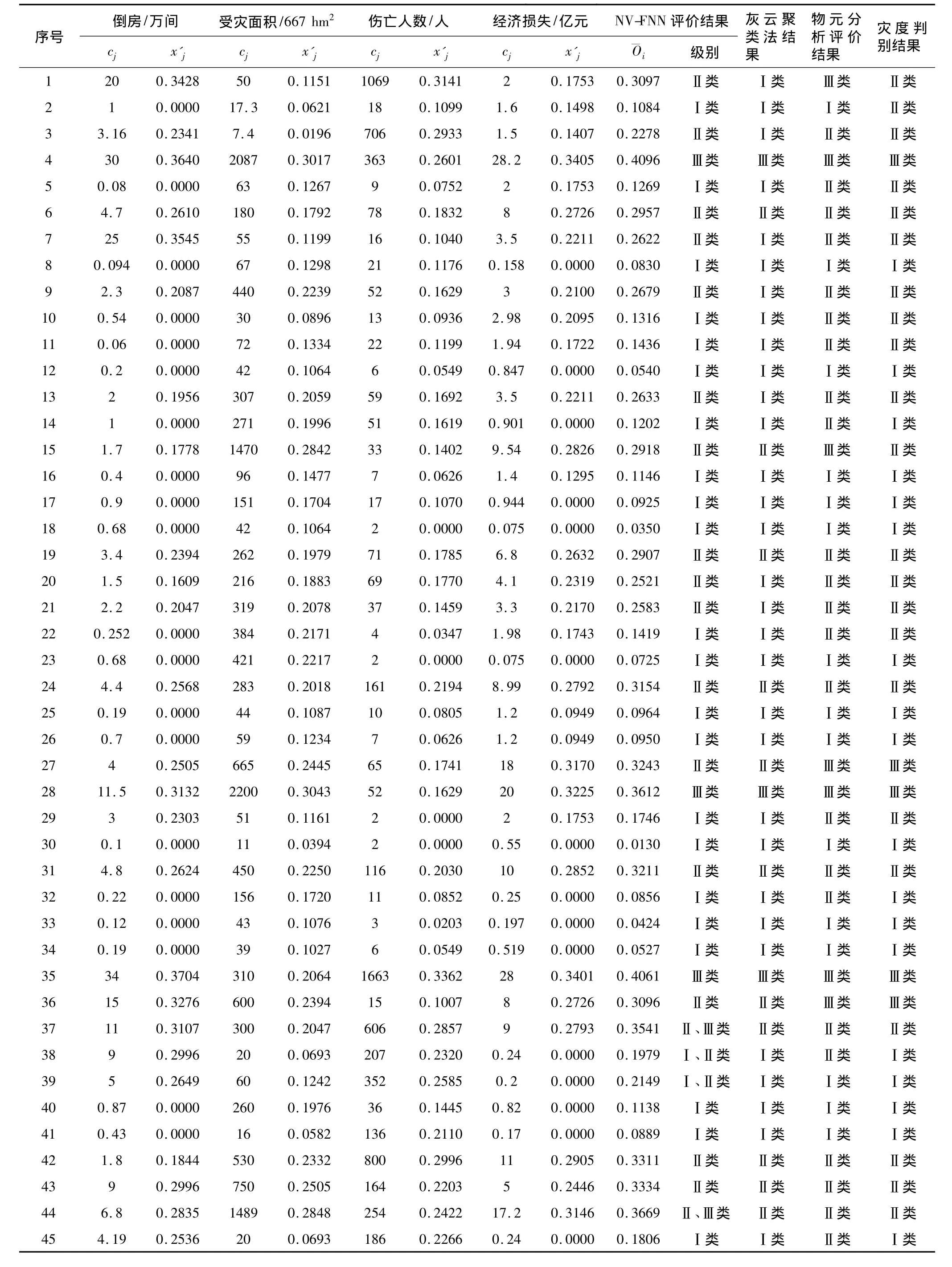
表2 中国部分省市45个洪水灾害案例监测值cj、规范值和多种方法评价结果

灾度判倒房/万间 受灾面积/667 hm2 伤亡人数/人 经济损失/亿元 NV-FNN序号别结果评价结果cj x'j cj x'j cj x'j cj x'j ¯Oi 级别灰云聚类法结果物元分析评价结果1 20 0.3428 50 0.1151 1069 0.3141 2 0.1753 0.3097 Ⅱ类 Ⅰ类 Ⅲ类 Ⅱ类2 1 0.0000 17.3 0.0621 18 0.1099 1.6 0.1498 0.1084 Ⅰ类 Ⅰ类 Ⅰ类 Ⅱ类3 3.16 0.2341 7.4 0.0196 706 0.2933 1.5 0.1407 0.2278 Ⅱ类 Ⅰ类 Ⅱ类 Ⅱ类4 30 0.3640 2087 0.3017 363 0.2601 28.2 0.3405 0.4096 Ⅲ类 Ⅲ类 Ⅲ类 Ⅲ类5 0.08 0.0000 63 0.1267 9 0.0752 2 0.1753 0.1269 Ⅰ类 Ⅰ类 Ⅱ类 Ⅱ类6 4.7 0.2610 180 0.1792 78 0.1832 8 0.2726 0.2957 Ⅱ类 Ⅱ类 Ⅱ类 Ⅱ类7 25 0.3545 55 0.1199 16 0.1040 3.5 0.2211 0.2622 Ⅱ类 Ⅰ类 Ⅱ类 Ⅱ类8 0.094 0.0000 67 0.1298 21 0.1176 0.158 0.0000 0.0830 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类9 2.3 0.2087 440 0.2239 52 0.1629 3 0.2100 0.2679 Ⅱ类 Ⅰ类 Ⅱ类 Ⅱ类10 0.54 0.0000 30 0.0896 13 0.0936 2.98 0.2095 0.1316 Ⅰ类 Ⅰ类 Ⅱ类 Ⅱ类11 0.06 0.0000 72 0.1334 22 0.1199 1.94 0.1722 0.1436 Ⅰ类 Ⅰ类 Ⅱ类 Ⅱ类12 0.2 0.0000 42 0.1064 6 0.0549 0.847 0.0000 0.0540 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类13 2 0.1956 307 0.2059 59 0.1692 3.5 0.2211 0.2633 Ⅱ类 Ⅰ类 Ⅱ类 Ⅱ类14 1 0.0000 271 0.1996 51 0.1619 0.901 0.0000 0.1202 Ⅰ类 Ⅰ类 Ⅱ类 Ⅰ类15 1.7 0.1778 1470 0.2842 33 0.1402 9.54 0.2826 0.2918 Ⅱ类 Ⅱ类 Ⅲ类 Ⅱ类16 0.4 0.0000 96 0.1477 7 0.0626 1.4 0.1295 0.1146 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类17 0.9 0.0000 151 0.1704 17 0.1070 0.944 0.0000 0.0925 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类18 0.68 0.0000 42 0.1064 2 0.0000 0.075 0.0000 0.0350 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类19 3.4 0.2394 262 0.1979 71 0.1785 6.8 0.2632 0.2907 Ⅱ类 Ⅱ类 Ⅱ类 Ⅱ类20 1.5 0.1609 216 0.1883 69 0.1770 4.1 0.2319 0.2521 Ⅱ类 Ⅰ类 Ⅱ类 Ⅱ类21 2.2 0.2047 319 0.2078 37 0.1459 3.3 0.2170 0.2583 Ⅱ类 Ⅰ类 Ⅱ类 Ⅱ类22 0.252 0.0000 384 0.2171 4 0.0347 1.98 0.1743 0.1419 Ⅰ类 Ⅰ类 Ⅱ类 Ⅱ类23 0.68 0.0000 421 0.2217 2 0.0000 0.075 0.0000 0.0725 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类24 4.4 0.2568 283 0.2018 161 0.2194 8.99 0.2792 0.3154 Ⅱ类 Ⅱ类 Ⅱ类 Ⅱ类25 0.19 0.0000 44 0.1087 10 0.0805 1.2 0.0949 0.0964 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类26 0.7 0.0000 59 0.1234 7 0.0626 1.2 0.0949 0.0950 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类27 4 0.2505 665 0.2445 65 0.1741 18 0.3170 0.3243 Ⅱ类 Ⅱ类 Ⅲ类 Ⅲ类28 11.5 0.3132 2200 0.3043 52 0.1629 20 0.3225 0.3612 Ⅲ类 Ⅲ类 Ⅲ类 Ⅲ类29 3 0.2303 51 0.1161 2 0.0000 2 0.1753 0.1746 Ⅰ类 Ⅰ类 Ⅱ类 Ⅱ类30 0.1 0.0000 11 0.0394 2 0.0000 0.55 0.0000 0.0130 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类31 4.8 0.2624 450 0.2250 116 0.2030 10 0.2852 0.3211 Ⅱ类 Ⅱ类 Ⅱ类 Ⅱ类32 0.22 0.0000 156 0.1720 11 0.0852 0.25 0.0000 0.0856 Ⅰ类 Ⅰ类 Ⅱ类 Ⅰ类33 0.12 0.0000 43 0.1076 3 0.0203 0.197 0.0000 0.0424 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类34 0.19 0.0000 39 0.1027 6 0.0549 0.519 0.0000 0.0527 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类35 34 0.3704 310 0.2064 1663 0.3362 28 0.3401 0.4061 Ⅲ类 Ⅲ类 Ⅲ类 Ⅲ类36 15 0.3276 600 0.2394 15 0.1007 8 0.2726 0.3096 Ⅱ类 Ⅱ类 Ⅲ类 Ⅲ类37 11 0.3107 300 0.2047 606 0.2857 9 0.2793 0.3541 Ⅱ、Ⅲ类 Ⅱ类 Ⅱ类 Ⅱ类38 9 0.2996 20 0.0693 207 0.2320 0.24 0.0000 0.1979 Ⅰ、Ⅱ类 Ⅰ类 Ⅱ类 Ⅰ类39 5 0.2649 60 0.1242 352 0.2585 0.2 0.0000 0.2149 Ⅰ、Ⅱ类 Ⅰ类 Ⅰ类 Ⅰ类40 0.87 0.0000 260 0.1976 36 0.1445 0.82 0.0000 0.1138 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类41 0.43 0.0000 16 0.0582 136 0.2110 0.17 0.0000 0.0889 Ⅰ类 Ⅰ类 Ⅰ类 Ⅰ类42 1.8 0.1844 530 0.2332 800 0.2996 11 0.2905 0.3311 Ⅱ类 Ⅱ类 Ⅱ类 Ⅱ类43 9 0.2996 750 0.2505 164 0.2203 5 0.2446 0.3334 Ⅱ类 Ⅱ类 Ⅱ类 Ⅱ类44 6.8 0.2835 1489 0.2848 254 0.2422 17.2 0.3146 0.3669 Ⅱ、Ⅲ类 Ⅱ类 Ⅱ类 Ⅱ类45 4.19 0.2536 20 0.0693 186 0.2266 0.24 0.0000 0.1806 Ⅰ类 Ⅰ类 Ⅱ类 Ⅰ类

(4)模型不足之处为对多指标的前向网络建模，将其分解为2-2-1和(或)3-2-1两种结构可以有多种不同的组合模式，某些情况下，不同的组合得到评价结果有一定差异。

［1］ Schmidt S，Kemfert C，Hoppe P.The impact of social-economics and climate change on tropical cyclone losses in the USA［J］.Regional Environmental Change，2010，10(1):13-23.

［2］ Ologunorisa T E.An assessment of flood vulnerability zones in the Niger delta，Nigeria［J］.Intern J Environ Studies，2004，61(1):31-38.

［3］ Jose I.Barredo.Major flood disasters in Europe:1950-2005［J］.Natural Hazards，2007，42:125-148.

［4］ 王健，黄敏，薄景山.地震灾害损失评估新方法［J］.自然灾害学报，2014，23(2):221-225.

［5］ 葛鹏，岳贤平.洪涝灾害评估研究综述［J］.南通大学学报(自然科学版)，2012，11(4):68-74.

［6］ 李祚泳，杨怀金，燕鹏.基于免疫进化算法优化的灾情评估指数公式及效果检验［J］高原气象，2004，23(4);553-557.

［7］ 张弛，宋绪美，李伟.可变模糊评价法在洪涝灾情评价中的应用［J］.自然灾害学报，2008，17(5):34-39.

［8］ 陈亚宁，杨思全.灰色聚类在洪水灾害等级划分中的应用［J］.干旱区地理，1999，03:37-42.

［9］ 李祚泳，邓新民.自然灾害的物元分析灾情评估模型初探［J］.自然灾害学报，1994，3(2):28-33.

［10］ 刘少军，张京红，何政伟，等.改进的物元可拓模型在台风灾害预评估中的应用［J］.自然灾害学报，2012，21(2):135-141.

［11］ 郭小东，李宁，苏经宇.基于集对分析理论的洪水灾情综合评估方法［J］.中国安全生产科学技术，2011，10:51-55.

［12］ 魏一鸣，范英，傅继良，等.基于神经网络的洪水灾害预测方法［J］.中国管理科学，2000，8(3):57-62.

［13］ 董四辉，宿博，赵宇库.基于投影寻踪技术的洪水灾情综合评价［J］.中国安全科学学报，2012，12:64-69.

［14］ 刘德地，陈晓宏.基于支持向量机的洪水灾情综合评价模型［J］.长江流域资源与环境，2008，17(3):490-494.