基于BP神经网络的谐波电流检测方法研究

单冬红，蔡琪，鲁书喜

（1.平顶山学院河南平顶山467000；2.平顶山教育学院河南平顶山467000）

基于BP神经网络的谐波电流检测方法研究

单冬红1，蔡琪2，鲁书喜1

（1.平顶山学院河南平顶山467000；2.平顶山教育学院河南平顶山467000）

谐波检测环节的性能对于有源滤波器的谐波治理能力有着重要的影响。目前应用最广泛的ip_iq谐波检测算法，其需要复杂的坐标变换，同时还需要用到锁相环以及低通滤波环节，结构复杂。为克服ip_iq算法的以上缺点，文中提出一种基于BP神经网络的谐波检测算法，只需将检测到的三相负载电流以及程序生成的A相模拟旋转角作为系统的输入，通过神经网络的计算便可以得到三相基波电流，再用负载电流减去基波电流便可以得到需补偿的谐波成分。通过Mat1ab仿真验证了算法的有效性。

谐波检测；神经网络；有源滤波器；基波电流

目前应用最为广泛是基于瞬时无功功率理论的谐波检测算法，其可以快速有效的检测出所需补偿的谐波成分，但算法所需坐标变换运算繁杂，而锁相环易受电压畸变影响，低通滤波器带来的系统延迟也是无法避免的。随着智能技术的发展，神经网络在谐波检测方面的应用潜力也被越来越多的专家所发掘。相对于ip_iq谐波检测算法，其不需要繁杂的数学计算，也不需要锁相环以及低通滤波环节，大大降低了系统的复杂性，减小了系统的检测延迟，提高了系统的检测性能。在文献［1］提出的6_41_3结构的BP神经网络以三相电流的采样值和一个周期内三相电流的最大值作为神经网络的输入，输出为三相基波电流的幅值。再将基波电流的幅值乘以由锁相环输出的各项基波同相位的单位基波信号便得到了基波分量，其算法结构还是过于复杂，由于锁相环的加入，也增加了系统受干扰的几率。相对于上述BP神经网络，文献［2］提出的4_9_3结构的神经网络在实现谐波的精确检测的同时结构上也大为精简。但其将三相负载电流和A相电压值作为系统的输入，当系统电压存在畸变时，由于A相电压的引入将会影响系统的检测精度。本文提出一种三层（4_10_3）BP神经网络谐波检测算法，以三相负载电流以及程序生成的模拟A相电压旋转角作为输入，输出为三相基波电流，隐层节点数为10。与以上文献中提出的神经网络相比，结构简单，同时将程序生成的模拟A相电压旋转角作为一个输入量既避免了因采用电压量可能带来的干扰也避免了因使用锁相环对检测精度带来的影响［3］，提高了系统的检测性能。

1　有源滤波器谐波补偿原理

有源滤波器运行原理如图1所示，将采集到的三相负载电流和A相电源电压输入控制器，通过检测出需要补偿的谐波成分，控制器产生PWM信号控制逆变器输出待补偿谐波电流［4_5］，从而对谐波进行治理。控制器部分包括谐波检测部分以及电流跟踪控制部分。

2　BP神经网络

谐波检测部分采用BP神经网络。BP神经网络是至今为止应用最广泛的神经网络，在实际工程应用中，以单隐层的BP神经网络应用最为普遍。一般将单隐层感知器称为三层感知器，包括输入层、隐层、输出层。其结构如图2所示。

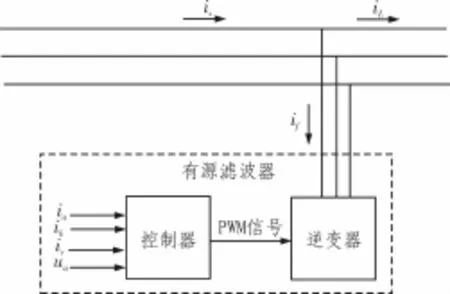
图1　有源滤波器运行原理

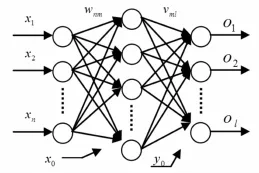
图2　BP神经网络结构

在三层感知器结构中，X=（x1，x2，x3，…，xn）T为输入向量，x0为隐层设置的阈值；Y=（y1，y2，y3，…，yn）T为隐层的输出向量，y0为输出层的阈值；0=（o1，o2，o3，…，ol）T为输出层的输出向量；D= （d1，d2，d3，…，dl）T为神经网络的期望输出。wnm表示输入层第n个节点到隐层第m个节点所对应的权值；vml表示隐层第m个节点到输出层第l个节点所对应的权值。各层信号之间有如下数学关系：

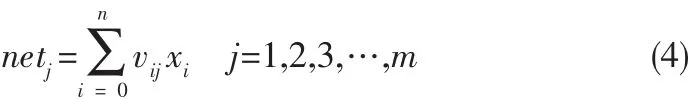
在上式中转移函数f（x）为单极性Sigmoid函数：

单极性Sigmoid函数具有连续可导的特点，其导数为：

或者双极性Sigmoid函数（双曲线正切函数）：

BP网络学习算法采用误差反传算法（Error Back Propagation A1gorithm），当输出层的实际输出与期望输出不相等时定义误差函数，将误差反向传播，以误差函数梯度为依据修正各层权值，使得误差不断减小。下面以三层BP神经网络进行说明。

当网络输出与期望输出不等时，定义误差为：

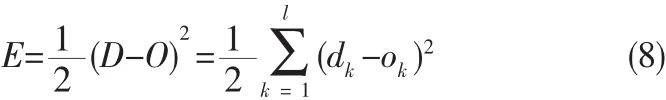
将误差展开至隐层：

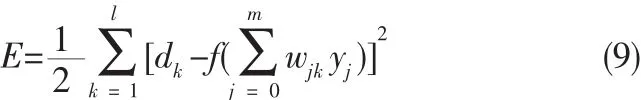
将误差进一步展开至输入层：

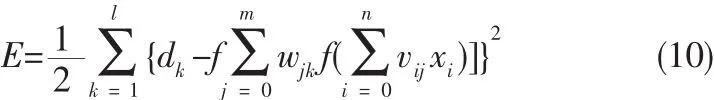
由式（8）、（9）可以看出网络误差是各层权值的函数，因此调整权值可以改变误差。权值的调整原则是使误差不断减小，因此权值的调整量应与误差的梯度下降成正比，则权值的调整量为：

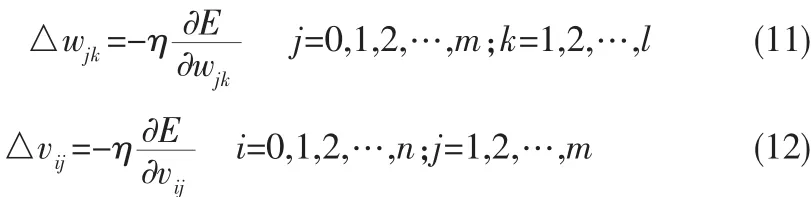
负号表示梯度下降，η∈（0，1）为学习率。

3　基于BP神经网络的谐波检测

因为有源滤波器是对各次谐波进行整体补偿，所以只要检测出负载电流中的基波分量，再用负载电流减去基波分量便可得到需补偿的谐波分量。因为负载电流和基波电流之间并非是简单的单值函数关系，若直接将三相负载电流作为BP神经网络的输入，如图3所示，三相基波电流作为期望输出对神经网络进行训练，神经网络无法准确的检测出基波电流。考虑再引入一项附加量对负载电流进行标注以改善神经网络的检测性能［6_7］。考虑到三相负载电流是周期变化的，引入的附加量应该也是周期变化且同负载电流同周期，为简化计算，附加量函数表达式应该尽可能的简单。系统相电压的旋转角是取值范围为0～2π的单调递增函数，可以满足上述附加量的要求。为了进一步的简化计算，实验中放弃锁相环，采用软件编程来产生A相电压的模拟旋转角。

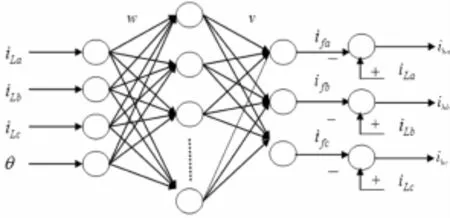
图3　三层BP神经网络结构示意图

以三相负载电流以及A相电压的模拟旋转角作为输入，三相基波电流作为输出建立三层BP神经网络，隐层选择10个节点。A相电压模拟旋转角采用软件的方式生成，和A相电压同周期，取值范围为0～2 π，公式为：

其中fa是A相基波频率为50 Hz，t为时间，Φ为初相。仿真时，模拟有源滤波器在A相电压正向过零点时启动，故初相为零。

负载为三相桥式整流电路带非线性负载，负载电阻为R= 15 Ω，负载电感为L=0.020 H。当系统稳定运行4个基波周期后，将采集到的1个基波周期的三相负载电流和通过程序生成的模拟A相电压旋转角度组成神经网络的输入数据，利用ip_iq谐波检测算法得到的三相基波电流数据组成神经网络的期望输出数据，训练数据总共20 000组。

利用Mat1ab提供的神经网络函数建立4_10_3三层BP神经网络，输入为三相负载电流以及模拟A相电压旋转角，输出为三相基波电流，如图4所示。选择tansig函数作为隐层神经元传递函数，输出层神经元的传递函数也为pure1in函数，训练函数选择train1m函数，迭代次数设置为600次。由图5所示，当迭代次数达到600次时，均方误差为0.002 790 8。

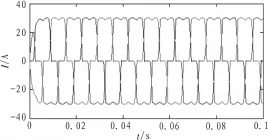
图4　三相负载电流波形

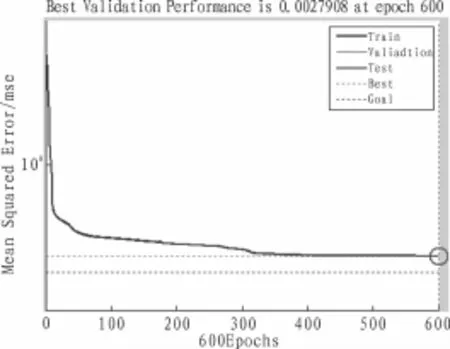
图5　训练均方误差曲线

将训练好的网络用于三相负载电流检测，代入采集到0～0.1 s的三相负载电流数据，检测得到的三相基波电流波形如图6所示。

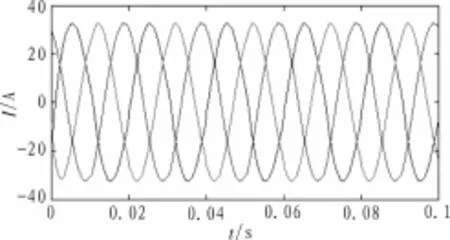
图6　三相基波电流波形

对其中A相电流进行频谱分析，可以得出由神经网络检测得到的系统三相电流基本上只含有50 Hz基波成分，其他的谐波成分得到了有效的滤除。最终得到的A相待补偿谐波电流波形如图7所示。

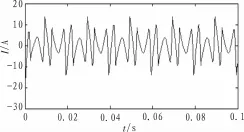
图7　A相待补偿谐波电流

神经网络算法最终得到的A相待补偿谐波电流波形与ip_iq算法检测得到的A相待补偿谐波电流波形（图8）对比可知，ip_iq算法因存在大约1/3工频周期的延时，在0.01 s之前的检测结果与实际谐波电流相差较大，而BP神经网络因为延时很小，其结果更加的精确。

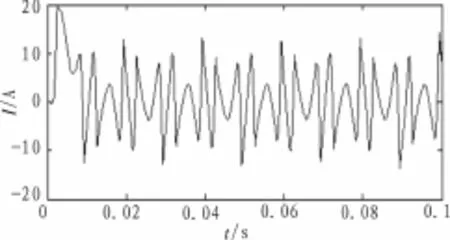
图8　由ip_iq算法检测的A相谐波电流

4　结论

本文提出的基于BP神经网络的检测算法结构简单，能够有效的检测出系统的基波电流，进而求得所需补偿的谐波电流，既可用于三相谐波检测，也可用于单相谐波检测。相对于ip_iq谐波检测算法来说，不需要繁杂的坐标变换以及大量的数学运算，由于省去了低通滤波环节，大大降低了系统延迟，以程序生成模拟A相电压旋转角也省去了锁相环的使用，提高了系统的可靠性。Mat1ab仿真证明本文提出的BP神经网络谐波检测算法可以快速有效的检测出所需补偿的谐波分量。

［1］马立新，林家隽，肖川，等.电流突变抑制与智能化谐波检测系统［J］.电力系统及其自动化学报，2012，24（1）：49_53.

［2］岳明道，郭焕银，李文艺.一种基于神经网络的电力谐波检测方法［J］.仪表技术，2010（12）：1_4.

［3］马立新，肖川.神经网络与锁相环相结合的谐波检测方法［J］.电力系统及自动化学报，2011，23（3）：24_29.

［4］张谦，王好娜，付志红，等.滤波器_神经网络的谐波检测方法［J］.电力系统保护与控制.2011，39（12）：42_47.

［5］陈淑华，付青，马桂龙，等.基于神经网络自适应预测算法的谐波检测［J］.电工技术学报，2011，26（增刊1）：200_206.

［6］王旻鹤，刘一江，彭楚武.模糊神经网络优化间谐波检测方法［J］.电力系统及自动化学报，2011，23（3）：118_122.

［7］商红桃.三相不平衡电网谐波电流检测方法的研究［J］.自动化技术与应用，2013，32（12）：74_77.

Research on harmonlc current detectlon based on BP neural netWork

SHAN Dong_hong1，CAI Qi2，LU Shu_xi1
（1.Pingdingshan University，Pingdingshan 467000，China；2.Pingdingshan Education College，Pingdingshan 467000，China）

The performance of harmonic detection has an important effect on the abi1ity of active power fi1ter harmonic compensation.At present，the most wide1y used harmonic detection a1gorithm is ip_iq a1gorithm.it needs comp1ex coordinate transformation and needs to use phase_1ocked 1oop and 1ow pass fi1ter，so its structure is very comp1ex.In order to overcome the disadvantages of the above a1gorithms，this paper proposes a harmonic detection a1gorithm based on BP neura1 network，on1y use the three phases of 1oad current and the rotation ang1e of A phase generated by the program as the inputs of the system，we can get the three_phase fundamenta1 current by the neura1 network computing，and harmonic components can be obtained by subtracting fundamenta1 current from the 1oad current.Mat1ab simu1ation verified the effectiveness of the a1gorithm.

harmonic detection；neura1 network；active power fi1ter；fundamenta1 current

TN802

A

1674_6236（2016）10_0042_03

2015_06_15稿件编号：201506148

河南省教育厅科学技术研究重点项目资助计划（14B460011）

单冬红（1976—），女，河南邓州人，硕士，副教授。研究方向：数据挖掘、算法分析。