公钥加密算法LUC的并行实现方法
杜珍珍,陆正福,周 同,杨春尧,3
(1.云南大学 数学与统计学院,云南 昆明 650091;2.铜陵职业技术学院,安徽 铜陵 244000;3.卫士通信息产业股份有限公司,四川 成都610041)
公钥加密算法LUC的并行实现方法
杜珍珍1,2,陆正福1,周同1,2,杨春尧1,3
(1.云南大学 数学与统计学院,云南 昆明 650091;2.铜陵职业技术学院,安徽 铜陵 244000;3.卫士通信息产业股份有限公司,四川 成都610041)
LUC是基于数论的公钥密码体制,相比RSA公钥密码体制,具有能够抵抗共模攻击的优点。但LUC算法因实现难度大,运算时间长而难以用于实际加密。而影响其运算速度的主要因素是密钥长度和模幂算法。本文参考相关文献工作,得到将密钥进行分段计算的公式,而后利用LUC序列的性质将密钥进行分段计算,并在多核系统下实现了LUC并行算法,从而提高了LUC算法的执行效率。
Lucas序列;密码体制;密码算法
以Lucas序列[1,2]为基础构造的公钥密码体制——LUC密码体制,是一种可以替代RSA的密码体制,同时LUC算法同RSA算法一样建立在大整数分解(BIF)的数学难题上,并也是以推广欧拉定理为基础的。在选定的消息直接做数字签名时,RSA密码体制可能遇到适应性攻击,LUC密码体制由于不具有乘法的封闭性,可以抵御这种适应性攻击,因此LUC安全性高于RSA[3]。但是LUC一般的实现方法耗时太多,对其快速算法的研究具有重要意义。
本文对LUC密码体制进行研究,设计并行算法,并对其复杂度进行分析,实验证明该算法的实现效率高于原有算法[4,5]。
1 基础知识
设P是一个正整数,Lucas序列具有下列二阶线性关系:Ts=PTs-1-QTs-2,s≥2,从而其特征方程为x2-Px+Q=0,其根为表示D的平方根),其中D是方程的判别式,D=P2-4Q。如果选P,使D≠0,则Lucas数列可定义为:

这里仅给出本文中所用到的几个重要性质:
性质 1[1]设a,b是任意正整数,则有
性质2[1]设n是任意正整数,则有
性质3[1]设n是任意正整数,则有
性质4[5]设m,n是任意正整数且m>n,则有Um+n=UmVn-QnUm-n。
性质5[5]设m,n是任意正整数且m>n,则有Vm+n=VmVn-QnVm-n。
性质 6[1]设 m,n是任意正整数,则有2Vm+n=VmVn+DUmUn(其中D=P2-4Q)。
性质7[2]设m,n是任意正整数,则有2Um+n=UmVn+UnVm。
2 LUC密码体制
①取两个不同的大素数 f,w(保密);
③随机选取整数e,满足(gcd)(e,ϕ)
N=1;
④计算d,满足de=1(modϕ)(N),同时删除f,w(其中N,e为公钥,d为私钥);
加密:由线性关系Ts=PTs-1-QTs-2,设其特征方程的根为α,β,则有
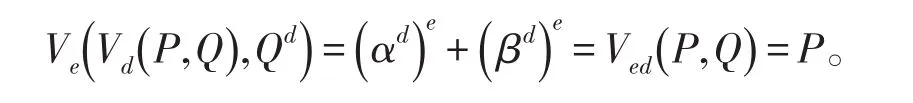
3 LUC密码算法
3.1计算Vk(P,Q 的递归算法
设P,Q是两个正整数,且P2-4Q是一个非完全平方数,利用性质2和性质3设计递归算法。当输入的数为偶数时执行性质2式,当输入的数为奇数时,执行性质3式,具体算法如下:算法名称:计算Vk(P,Q)的递归算法

此算法由于采用递归方法,它的时间复杂度为O (log2k),但当k较大时,实现效率较低。
3.2计算Vk(P,Q)的快速递推算法
设P是正整数,且P2-4Q是一个非完全平方数,对于∀k≥1,由性质2、性质3及文献[4]设计实现Vk( P,Q)的快速算法。
算法名称:计算V(P,Q) 的快速递推算法[2]
算法伪码描述如下:

此算法的实现复杂度为O (log2k),实现效率相对较高。
3.3输出Uk-Vk的快速递推算法
在算法3.2的基础上,实现输出Uk-Vk的算法。在文献[5]中,设k>0,把k用二进制表示,令
Kj-1=kj-1+2Kj=Kj+kj-1+Kj。
由性质4和性质5有下列关系:
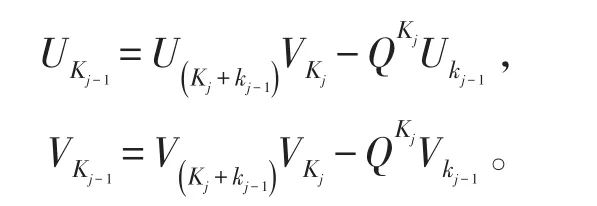
具体算法如下:
算法名称:计算Uk-Vk的快速递推算法[5]
输出:(Uk,Vk)
算法描述如下:


此算法是递推算法,它的实现复杂度为O (log2k),实现效率接近于算法3.2。
3.4输出Uk-Vk的并行算法
此算法是在算法3.3的基础,把k的2进制表示按20:21:22:…:2t的比例划分为t+1段,分多个进程分别计算[7],然后多次使用性质6和性质7计算出Vk和Uk,这里
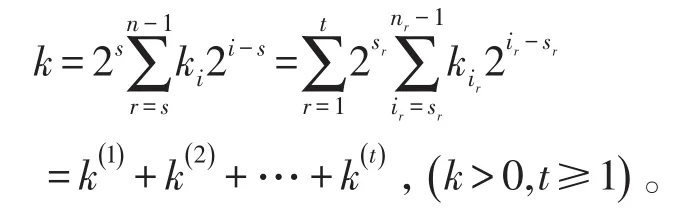
该算法适用于多核系统,将密钥分割成多个部分,每部分又有高位段和低位段,首先需要对每部分的高位段密钥进行低位补零,然后将该部分密钥分别交由两个进程执行。其余部分的进程任务依此类推,具体算法如下:
算法名称:输出Uk-Vk的并行算法
输入:k
输出:Uk,Vk
算法伪码描述:
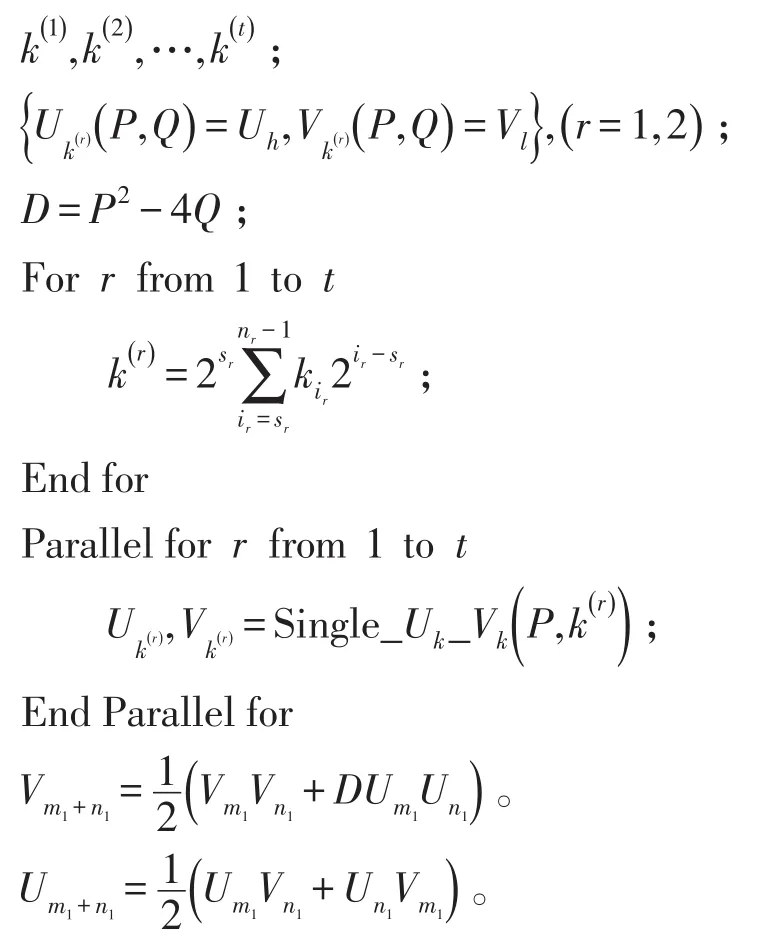
此种实现方法的算法复杂度是O (log2k),但由于使用多个处理器系统并行计算,实现速度快于前面的两个算法[4,5]。
为了使算法3.4更容易理解,下面用一个图形来进行说明。图中的(1),(2),(3),(4)表示文中
如图1,进程1、进程2、进程3和进程4分别计算出U(1)和V(1)、U(2)和V(2)、U(3)和V(3)及U(4)和V(4),利用性质6和性质7进行下面的计算:
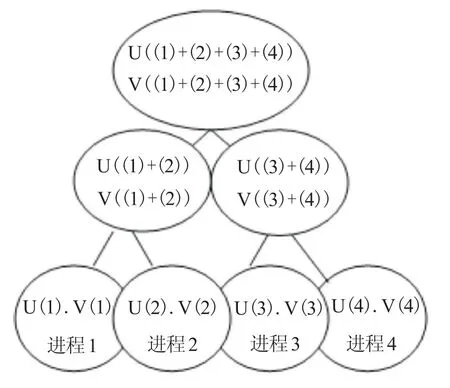
图1 给四个进程分配任务
将U(1)和V(1)与U(2)和V(2)及U(3)和V(3)与U(4)和V(4)可以分别合并出U((1)+(2))和V((1)+(2))及U((3)+(4))和V((3)+(4)),最后再由U((1)+ (2))和V((1)+(2))与U((3)+(4))和V((3)+(4))合并出U((1)+(2)+(3)+(4))和V((1)+(2)+(3)+(4))。
4 实验分析
接下来测试本文中的相关算法运行时间。实验在Windows环境下进行,并行算法采用MPI机制来实现,编译器为VC++6.0,实验中采用的机器配置为:Intel Pentuim D双核处理器(1.9 GHz),内存1 GB。取随机数m(即加密体制中的明文编码)的长度为一定值,随机素数 p,q都为密钥k (k=m+n)长度的一半,对于不同的密钥长度,计算Vk的快速算法[4]、计算Uk-Vk的快速算法[5]、计算Uk-Vk的并行算法运行时间(此算法在文献[5]的基础上设计的),在mpich2环境下执行之后,得到了串行和并行算法的部分计算时间如表1所示。

表1 本文中的两种算法在不同密钥长度下的执行时间
根据表1绘制得到图2,从图2中可以看到在密钥长度较短的时候,串行算法要略优于并行算法,这是由于并行的两个进程间通信需要消耗一定时间,但是随着密钥长度的增加,并行算法要优于串行算法,尤其是在重负载(密钥长度大于1 000 b)的情况下表现得更明显。根据实验结果,计算Vk的并行算法理论加速比约为1.33,实际加速比为1.22。
从实验结果来看,对于本文提出的并行LUC算法,并不是使用的进程越多,执行的速度就会更快。因为当进程开启较多的时候,系统对进程的调度、进程间的通信、进程间的等待所消耗的时间是不可忽略的,从图2中看到,在1万比特以下的密钥长度,4个进程的执行时间会比2个进程的执行时间要短,但当密钥长度超过1万比特时,采用2个进程的执行效果要比4个进程理想得多。

图2 本文中的两种算法在不同密钥长度下的执行时间
5 结语
LUC公钥密码体制是一种可以替代RSA的一种新体制,但其实现效率相对较低,此问题不解决就难以实际应用,因此,对其快速算法的研究备受密码学界的高度重视。因此,本文在分析研究前人设计的LUC密码算法的基础上,设计LUC密码快速实现算法,通过理论分析与实验表明,本算法能够提高LUC的运算效率[5]。
[1] Smith P.LUC Public-Key encryption[J].Dr.Dobb's Journal,1993,18(1):44-49.
[2] 孙琦,张起帆,彭国华.Dickson多项式ge(x,1)公钥密码体制的新算法[J].四川大学学报(自然科学版),2002,39(1):18-23.
[3] 罗相根,薛延平,刘益民.RSA公钥密码系统算法结构及其安全性[J].信息安全与通信保密,2006(8):119-120,124.
[4]Castagnos G.An efficient probabilistic public-key cryp-tosystem over quadratic fields quotients[J].Finite Fields and TheirApplications,2006,13(3):563-576
[5] Joye M,Jean-Jacques Q.Efficient computation of full Lucas se-quences[J].Electronics Letters,March,1996,32(6):537-538
[6] Knuth D E.The art of Computer Programming[M]. Semi-Numerical Algorithms,Addision-Wesley,Reading,MA,1981.
[7] 梁帅.RSA密码系统中的并行算法研究[D].呼和浩特:内蒙古大学,2008.
A parallel realization for LUC algorithm of public key cryptosystems
DU Zhen-zhen1,2,LU Zheng-fu1,ZHOU Tong1,2,YANG Chun-yao1,3
(1.School of Mathematics and Statistics,Yunnan University,Yunnan Kunming 650091,China;2.Tongling Polytechnic,Tongling Anhui,244000,China;3.Chengdu Westone Information Security Industry Co.,Ltd,Chengdu Sichuan 610041,China)
The LUC algorithm based on the number theory is one of the public key encryption,which resists common modulus attack comparing with the RSA public cyptosystem.But it is difficult for practical encryption and decryption as LUC is a long time of computing task.The main factor that affects the calculation speed of LUC encryption is key length and mode power algorithm.Reviewed with related
in this paper,we deduced the expression which computed by key division segmentation,then applying the mathematical properties of LUC sequences,and the LUC algorithm is computed by key division segmentation,which is executed parallelly by implemented on multi-core platform,consequently,the computation efficiency of LUC algorithm is improved.
Lucas sequence;Cryptography;Cryptographic algorithm
TP393
A
1004-4329(2016)02-070-04
10.14096/j.cnki.cn34-1069/n/1004-4329(2016)02-070-04
2016-01-05
杜珍珍(1984-),女,硕士,讲师,研究方向:信息安全、网络计算研究。

