基于用户领域知识优化ID3算法的研究与应用
王 森,赵发勇,陈曙光
(阜阳师范学院 物理与电子工程学院,安徽 阜阳 236041)
基于用户领域知识优化ID3算法的研究与应用
王森,赵发勇,陈曙光
(阜阳师范学院 物理与电子工程学院,安徽 阜阳 236041)
本文在ID3算法的基础上引入属性重要度因子和均衡化函数,对ID3算法进行优化,改进了经典ID3算法要求每个属性对类别属性的贡献一样的缺点,可以适用于不同属性对类别属性的贡献不同的情况,同时也弥补ID3算法偏向多值属性的不足。最后给出具体一个实例说明其构造决策树的过程,并将优化算法与经典ID3算法构造的决策树进行了比较,从而得出优化后的算法具有更大的适应范围,且更符合用户实际情况的需要。
决策树;ID3算法;属性重要度;均衡化函数
决策树算法是经常使用的一种分类算法,经典的决策树学习算法,如ID3算法[1]、C4.5算法[2]、CART算法[3]、CHILD算法[4]等,忽略了用户领域知识,认为各属性对分类属性的影响是一样,导致构造的的决策树不符合实际决策的情况。由于这种不足,所以在使用决策树算法时,用户要优化决策树算法。经典的ID3算法由于其使用范围很广,所以国内外许多学者提出方法对ID3算法进行改进,其中以C4.5算法[2]最为著名。
ID3算法是一个递归算法[1],具体计算过程如下:
首先,计算样本集正确分类的信息熵可由公式(1)计算:

其中,训练样本集S中有s个样本在m个不同类Ci(i=1,2,…,m)中,si是类Ci中的样本数,pi常用估计。
其次,根据每个侯选属性把样本分类后的信息熵由公式(2)计算:

其中 sij是属于子集Sj中类别Ci的样本个数,充当第j个子集的权。E(A)越小,子集纯度越高。
最后计算每个侯选属性A上的信息增益由公式(3)给出:
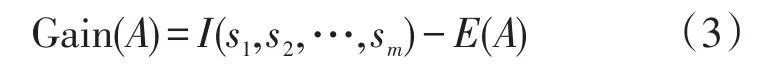
表示知道属性A的值而导致训练集的信息熵减小。
ID3算法计算并比较各侯选属性的信息增益值,选取具有信息增益最高的侯选属性作为测试属性。据该属性创建一个结点,并根据该属性的每个值创建该结点的分枝且划分样本;对于每个划分后的子样本集,递归调用该算法。ID3算法有两个不足,不使用领域知识(也是它的优点)和信息增益算法有选择多值属性的倾向,但多值属性未必是最优的测试属性;所以创建的决策树有时不符合实际的决策情况且效率低下。
文献[5-8]引进用户兴趣度对ID3算法作了改进,增加对用户感兴趣属性的重要性,把计算信息熵时加权和转换为权加用户兴趣度的和。某属性的信息熵E(A)改为并对用户兴趣度α的选取提出很好的建议,由决策者根据先验知识或领域知识测试后给出其大小,一般在[0,1]范围内。
1 基于用户领域知识决策树的理论基础
训练样本的每个属性对决策结果影响的重要性可能不同。在此情况下,若把它们同样的对待,并根据ID3算法得到的决策树,可能无法反映真实的决策情况。例如在学期末,学生课程的综合成绩,期末考试成绩的重要性要比平时上课出席情况、作业情况要高,而ID3算法把属性看为同等重要,构建的决策树不符合实际的决策过程;再比如,对于同一个数据集不同的用户可能有不同的要求:在买汽车时有的用户可能更注意汽车的安全性,对安全性有特殊的要求,而注重环保的用户,可能对节能或新能源有特殊的要求;在选择篮球运动员时,在同等的条件下,更注重身高的要求;在评价学生论文的成绩时更关注论文的有无创新性等,这样的例子在日常生活和工作中很常见;因此为了体现不同侯选属性对类别属性重要性的不同,笔者在计算各侯选属性的信息增益时,根据用户的先验知识,将候选属性对分类属性的重要性进行量化,引入了属性重要度参数α,不同的候选属性可以根据实际决策时该属性的重要性来设置,可以按比例对各属性进行设置,也可根据经验设置其中某个或某些属性的重要性。属性重要性α体现的是分类属性依赖候选属性的重要性,属性越关键越重要,α取值越大;反之,则属性重要性越小,α取值越小;若为0,则按照ID3算法考虑该属性。
另一方面,经典的ID3算法在选择测试属性时有选取多值属性倾向,而这些属性在实际情况下并不一定是最优测试属性,反而取值少的属性有可能为分类提供更有用的信息。因此,为了有效地解决偏向于取值较多的属性问题,引入了信息均衡化函数 f(N),它与属性值的个数N有相同的变化趋势,即随着N的增加而增加。当然 f(N)选择的好坏对结果也有很大的影响,已有学者证明C4.5算法中,就随着 N值的增加而增加。
在参考前人研究成果的基础上,结合自己实际研究工作,利用领域知识引入属性重要度或属性贡献度和信息增益均衡化处理[9-11],从而,增加用户对特别属性重要性的要求和降低ID3算法偏向多值属性的影响,在计算信息增益时,采用具体公式如下:
gain(属性)=(I(分类属性)-(1-α)E(属性)/f(N)(4)
公式(4)说明:
α是属性重要度,是表示该属性的重要性,越重要值越大,常常根据领域知识实验得到,其范围在0和1之间,即:0≤α≤1;
f(N)为信息增益均衡化函数,它与属性值的个数N有相同的变化趋势,即随着N值的增加,函数值也增加,最简单的取该属性的值的个数N;另外C4.5的spliti(A)函数就具有这种性质。
I(分类属性)是计算该数据样本集分类所需的期望信息;
E(属性)是该候选属性的信息熵;
gain(属性)是该候选属性的信息增益;
在计算并比较每个属性的信息增益后,选择信息增益最大的属性为测试属性,据此对样本空间进行划分。
对公式(4)的分析说明:
(ⅰ)属性对分类贡献越大,即重要性越大,α越大,最大值为1,即指定按照该属性进行分裂,反之,属性对分类贡献越小,即重要性越小,α越小,最小值为0,即与标准的ID3算法一样同等的考虑该属性;
( ⅱ)当α=0,f(N)=1时,该公式退化为标准ID3计算信息增益的公式;
(ⅳ)可以根据用户的要求任意指定某个或某些属性的的重要性α,而不必全部指定(当然也可以全部指定)。
此外为了加快构建决策树,在构建决策树时,可以根据用户指定的阈值采用先剪枝方法,使用统计度量,若要分裂的样本中有阈值以上样本属于同一个类时停止结点的分裂,构建叶子结点,并用多数表决来决定该结点的类别。
2 基于用户领域知识决策树算法
构建一个基于用户领域知识决策树算法如下:
算法名及参数说明:Gen_User_Dec_Tree(S,A,A_Importance)其中S是训练数据集,A是候选属性集,A_Importance是候选属性对应的重要性因子的集合。
算法功能:由要训练、学习的数据集产生一棵用户决策树。
输入:由离散属性表示训练数据集S;用于决策候选属性的集合A;每个用于决策候选属性对应的重要性因子的集合A_Importance。
输出:一棵用户决策树。
方法:
(ⅰ)由训练数据集S,创建节点N,该结点包含所有的训练数据集中所有数据样本;
( ⅱ)if S都在同一个类C,则返回N,并把该结点作为叶子节点,使用类C标记。
(ⅲ)else if A为空then返回N作为叶子节点,并以S中大多数样本所在的类别标记它或给出类分布。
(ⅳ)else统计侯选属性集合A中每个属性取值个数,即均衡化因子f(N)取为属性值个数n,并和A_Importance一起利用公式:
gain(属性)=(I(分类属性)-(1-α)E(属性)/f(N)其中α是该属性重要度,f(N)是均衡化因子,其中f (N)=n,n表示每个属性取值个数。计算侯选属性集合A中每个侯选属性的信息增益,把信息增益最大的属性选出作为测试属性Test_A。
■使用属性Test_A标记N;并根据属性Test_A中每个属性值ai,划分训练数据集S;相应的,由结点N生长一个条件为Test_A=ai的分枝;
■设Si是训练数据集S中属性Test=ai的样本数据的集合;如果Si为空则去掉该分枝或用S中大多数数据所在的类别标记;else加上一个由Gen_User_Dec_Tree(Si,A-Test_A,A_Importance-Test_A_Importance)返回的子树或结点。
3 基于用户领域知识决策树算法一个实际应用
由于本科毕业设计(论文)成绩一般从三方面考虑:①指导教师对学生的评价的有关数据并建议成绩等级。主要从完成“毕业论文任务”规定工作情况、学习态度、创新性评价、写作的规范性程度、存在的问题等方面。②评阅教师对设计(论文)评阅的情况并建议成绩等级,主要从论文选题的价值与意义、创新性评价、工作量的大小、写作规范化程度等各方面。③答辩小组对答辩情况的简述并建议成绩等级,主要从答辩态度、知识面、逻辑思维能力、口头表达能力、回答问题是否正确、语言是否流畅、对论文不足的认识、有关软件和硬件的演示情况的各方面考虑;三部分成绩组成学生的最终成绩。但不同单位,三部分成绩的比例不同,各种各样。
由于本科毕业论文成绩是由答辩小组决定的,为此笔者设计一个调查问卷,在毕业论文答辩时发给每个答辩小组,在答辩时要求答辩老师给予填写。调查表有关属性如下:学号、姓名、论文题目、论文格式(符合、基本符合、不符合)、论文有无创新(有、无)、论文的工作量(大、适中、小)、论文的实用价值(很大、一般)、答辩情况(好、一般、差)、论文的最终成绩(优、良、中、及格)。
从2014电子信息本科1班抽查若干名毕业设计答辩情况调查表和最终成绩,并综合考虑,经过属性相关性分析(去除不相关和弱相关的属性如学号、姓名、论文题目)、数据预处理(由于论文的格式由论文指导老师已经按要求对学生的论文进行严格把握,论文格式都基本符合论文要求,在此删除;对有关空缺值,根据毕业论文指导手册对有关数据进行补充或删除数据差别较大的数据值),数据转换后得到如下20名学生毕业设计答辩情况调查表和论文的最终成绩,并整理如表1。

表1 从2014电子信息本科1班毕业设计中抽查20名毕业设计情况调查表和最终成绩
其中分类属性为论文的最终成绩,其中优秀4个,良好6个,中等7个,及格3个。
首先,样本分类所需的期望信息为:

其次,在构建判定树时,特别给毕业设计中属性有无创新,增加一定的属性重要性因子α,说明在计算信息增益时强调其重要性,为了避免信息增益度量有倾斜具有许多值的属性,在计算信息增益时增加属性均衡化函数 f(N)=N,即除以该属性的值的个数N,从而降低多值属性对分类的影响。使用公式如下计算每个属性的信息熵:
gain(属性)=(I(分类属性)-(1-α)E(属性))/N,其中α是属性重要度因子,N是均值化函数,简单取为该属性的不同值的个数。
在下面的计算时,除了创新有无属性设α= 0.5之外,其余属性无属性重要度要求,另外,为了快速构建决策树和去除噪声,设用户的阈值为85%(即在要分类样本中,若有某一类的样本数占全部样本数的85%则停止该子树的构建)。
根据候选属性论文内容有无创新。统计属性论文内容有无创新的每个样本值:有创新和无创新,分别计算期望信息。
对于论文中有创新:优秀的有2个,良好的有4个,没有中等和及格的,则有:

对于论文中无创新的:成绩优秀的有2个,良好的有2个,中等的有7个,及格的有3个,则有:

则如果样本按论文有无创新划分,对此分类所需的期望信息为:
因此,由于创新属性的重要性设为0.5,故这种划分的信息增益是
Gain(创新)=(I(s1,s2,s3.s4)-(1-0.5)E(创新)/2=0.582 9。
同理,由于其余属性的重要性看为同等重要都设为0,使用ID3算法计算其信息增益,可得:
Gain(实用价值)=(I(s1,s2,s3.s4)-E(实用价值)/2=0.123 4;
Gain(工作量)=(I(s1,s2,s3.s4)-E(工作量)/3=0.106 4;
Gain(答辩情况)=(I(s1,s2,s3.s4)-E(答辩情况)/3=0.212 4。
比较上面四种属性的信息增益,创新性属性的信息增益最大,因此按设计有无创新属性划分实例样本,并对每一个划分后的样本空间,使用上面同样的方法,构件判定树的各分枝,最终构建判定树如图1。基于传统ID3构建的决策数如图2。

图1 基于强调创新属性α=0.5构建的毕业设计(论文)成绩决策树

图2 基于传统ID3算法构建的决策树
比较图1和图2:图1的创新结点提升到根结点,而具有多值属性的论文答辩情况下降为第二层,说明图1更强调创新在毕业论文成绩中的作用,同时它也避免了多值属性对决策树的影响,更符合当今强调创新精神社会中对大学生的要求,比较符合现今高校评价学生毕业论文的标准。
把图1决策树生成的分类规则,应用到其它毕业设计(论文)的成绩中进行准确评估,准确率达95%以上,当然对于与实际成绩不一致,也可以提供修改参考,分析其中的原由,并适当的进行调整,从而更客观的评定学生毕业设计(论文)成绩。
4 结束语
本文对ID3算法进行优化,增加属性重要性因子和属性均衡化函数,增加重要属性对分类的影响,同时也降低了多值属性对分类的影响,并构建自己的改进算法,且利用该算法对我校毕业生毕业设计(论文)成绩进行深入的挖掘,构建出对应的决策树,并提取出相应的分类规则且把它应用于实践,取得很好的效果,符合我校的实际情况。对现实中提取的数据集,应用这种增加属性重要性因子和属性均衡化函数改进方法,更符合客观现实情况的决策,准确率也较高。
[1] Han J W,Kamber M.数据挖掘(概念与技术)[M].北京:机械工业出版社,2006.
[2] K.P.Soman Shyam Diwakar V.Ajay.数据挖掘基础教程[M].北京:机械工业出版社,2011.
[3] Breiman L,Friedman J H,Olshen R A,and Stone C J.Classification and Regression Trees[J].Wadsworth,Belmont,1984.
[4] Mehta M,Agrawal R.SLIQ:A fast scalable classifier for data mining[J].int.conf.EDBT'96 28.
[5] 鲁为,王枞.决策树的优化及比较.计算机工程,2007,33(16):
[6] 张琳,陈燕,李桃迎,等.决策树分类算法研究[J].计算机工程,2011,37(13):66-67,70.
[7] 李道国,苗夺谦,俞冰.决策树剪枝算法的研究与改进[J].计算机工程,2005,31(8):19-21.
[8] 谢妞妞,刘於勋.决策树属性选择标准的改进[J].计算机工程与应用,2010,46(34):115-118,139.
[9] 喻金平,黄细妹,李康顺.基于一种新的属性选择标准的ID3改进算法[J].计算机应用研究,2012,29 (8):2895-2898,2908.
[10]孙淮宁,胡学钢.一种基于属性贡献度的决策树学习算法[J].合肥工业大学学报(自然科学版),2009,32 (8):1137-1141.
[11]王小巍,蒋玉明.决策树ID3算法的分析与改进[J].计算机工程与设计,2011,32(9):3069-3072,3076.
Study and application on the ID3 algorithm optimization based on user field knowledge
WANG Sen,ZHAO Fa-yong,CHEN Shu-guang
(School of Physics and Electonic Engineering,Fuyang Normal University,Fuyang Anhui 236041,China)
This paper introduces attribute importance factor and equalization function in ID3 algorithm,to optimize the ID3 algorithm.Improves on the classical decision tree algorithm requires that shortcomings of each attribute to the class attribute with the same importance,can be used in different attributes to the class attribute,but also make up for the disadvantages that the ID3 algorithm tends to multi valued attributes.At last,the process of constructing the decision tree is given,and the decision tree constructed by the classical ID3 algorithm is compared with the decision tree in the new method,which proved that there are more application fields and the more suited to the needs of users.
decision tree;ID3Algorithm;attribute importance;function of equilibrium;
中文分类号:TP391.6A
1004-4329(2016)02-065-05
10.14096/j.cnki.cn34-1069/n/1004-4329(2016)02-065-05
2015-10-25
安徽省科技攻关项目(12010302080)资助。
王森(1973-),男,硕士,讲师,研究方向:数据挖掘、软件工程。

