微细观尺度下欧拉梁的力学模型及有限元分析

贺　丹，陈　博，杨万里

(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)



微细观尺度下欧拉梁的力学模型及有限元分析

贺丹，陈博，杨万里

(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)

基于修正偶应力理论建立了仅含一个尺度参数且适用于各种边界条件的微尺度欧拉梁模型。基于哈密顿原理推导了微尺度欧拉梁的平衡微分方程，该方程与经典梁的平衡微分方程具有相似的形式，只是在弯曲刚度中多了一项与尺度效应有关的项，可直接用于分析和解释多尺度问题。提出了一种模量折算策略，从而利用经典梁单元即可完成对微细观尺度下的梁的弯曲、动力和稳定问题的求解。算例结果表明，在微细观尺度下梁结构将表现出比宏观状态下更强的抗弯刚度，即本文模型能捕捉到尺度效应。进一步的研究则指出，几何尺寸的大小是尺度效应的决定性因素。

修正偶应力理论；尺度效应；有限元；微尺度梁

近年来，微尺度下的尺度效应受到了广泛的关注，众多微尺度实验[1-6]证明，当构件的尺寸处于微/纳米量级时，试件的刚度和强度大于宏观尺寸下的刚度和强度，这种现象被称为尺度效应。在微尺度领域，由于尺度效应的存在使得传统的连续介质力学不再适用，因此人们发展了偶应力理论[7-13]和应变梯度理论等微极弹性理论来唯象地描述这种现象，其中偶应力理论相比应变梯度理论具有较少的特征尺度参数，因而更适合工程应用。Yang和Chong等人[11]提出的修正偶应力理论将特征尺度参数降为一个。基于修正偶应力理论，科研工作者建立了一系列微尺度板/梁模型[14-21 ]，并分析了其尺度效应。Park和Gao等人首先建立了欧拉梁的弯曲模型，并基于修正偶应力理论给出了微尺度欧拉悬臂梁弯曲的解析解[19]。另外，Park和Gao建立的微尺度欧拉悬臂梁模型捕捉到了弯曲的尺度效应，即与经典梁模型的挠度差随着梁厚度的减小而增大，这与实验结果吻合。尽管上述文章基于修正偶应力理论建立了微尺度欧拉梁模型且很好地分析了其微观特性，但其分析求解过程受边界条件的限制，不适合工程应用。

本文基于Yang和Chong[11]等人提出的仅包含一个特征尺度参数的修正偶应力理论建立了适用于任何边界条件的微尺度欧拉梁模型。基于哈密顿原理推导了微尺度欧拉梁的平衡微分方程，发现其与经典梁的平衡微分方程一致；故通过一次简单的模量折算采用有限元经典梁单元简单、有效地求解了平衡微分方程，非常适合工程应用。算例结果表明，本文悬臂边界条件下弯曲挠度的有限元结果与已有的文献相吻合，从而验证了本文方法的精度和可靠性，故进一步分析了不同边界条件下欧拉微梁弯曲挠度、自振频率和屈曲载荷的尺度效应。本文的有限元法亦可扩展应用于分析微尺度Kirchhoff板模型的微观特性。

1　欧拉微梁

1.1修正偶应力理论

修正偶应力理论由Yang[11]等提出，该理论中应变张量和曲率张量定义为

εij=(ui,j+uj,i/2)，χij=(ωi,j+ωj,i)/2

(1)

其中，ωi=eijkuk,j/2，eijk为轮换算符；u(ui)分别为沿x、y和z轴的平动位移，ωi分别为沿x、y和z轴的转动位移；εij和χij均是对称张量，分别表示应变和曲率。

基于修正偶应力理论，微尺度下的本构方程可表示为

σij=λεkkδij+2Gεij，mij=2l2Gχij

(2)

其中，λ和G为拉梅常数，l是微结构的特征尺度参数，δij为克罗内克符号，mij为偶应力矩分量，σij为应力分量。由于曲率张量是对称的，因此对于各向同性材料来说，其偶应力张量也是对称的。

1.2欧拉梁的基本方程

欧拉梁模型的位移场函数可表示为

(3)

其中，u、v和w分别为沿x、y和z轴的平动位移。梁模型如图1所示，x方向为梁长方向，z为梁厚度方向，Pb为临界载荷，fw为横向载荷，h为梁的厚度。

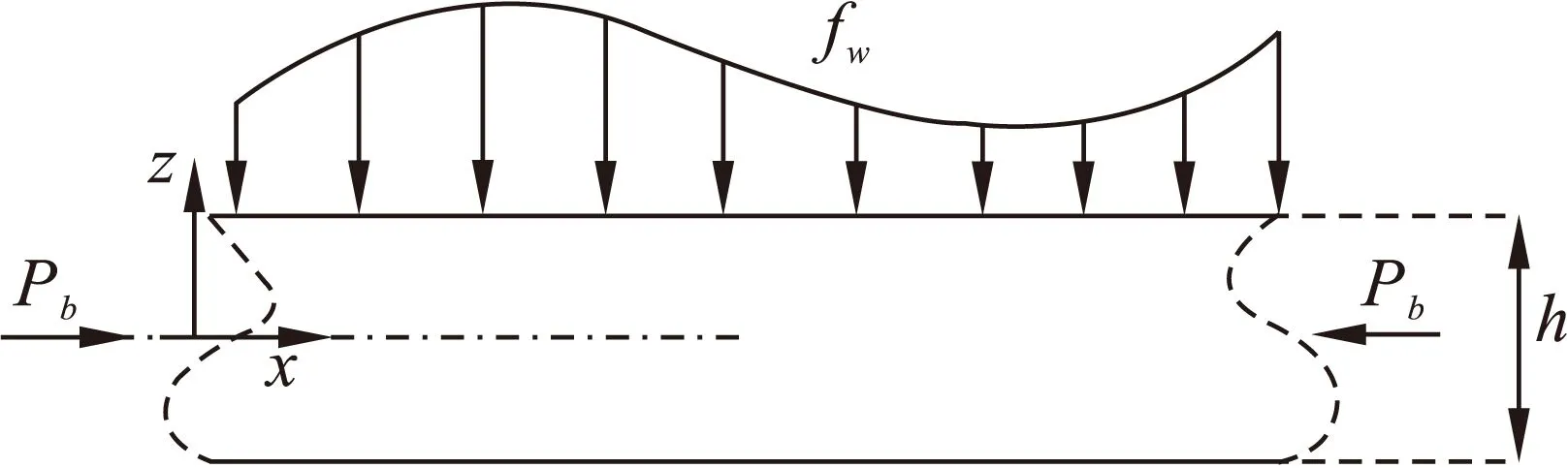
图1　欧拉梁示意图

将式(3)代入式(1)，则非零的应变和曲率分量可表示为

(4)

将式(4)代入本构方程(2)，则非零的应力和偶应力力矩分量为

(5)

其中，E和G分别为材料弹性模量和剪切模量。

2　梁的控制方程

基于修正偶应力理论，欧拉微梁的应变能可表示成

(6)

其中，U为应变能，V为梁的体积域，Pb为屈曲载荷，L为梁的长度。

将式(4)、(5)代入式(6)，则欧拉微梁的应变能可表示为

(7)

其中，A和I分别为截面的面积和惯性力矩。微梁的动能T可以写成

(8)

其中，ρ为材料密度，u是梁的平动位移。微梁的外力功W可以写成

(9)

其中，fw为横向载荷。

微梁的哈密顿原理表达如下

(10)

将式(7)和式(9)代入(10)，可得梁的平衡方程

(11)

其中，当Pb和∂2w/∂t2为零时，式(11)退化为欧拉微梁的弯曲模型；当Pb和fw为零时，式(11)退化为欧拉微梁的自由振动模型；当fw和∂2w/∂t2为零时，式(11)退化为欧拉微梁的稳定模型。若令l=0，则式(11)即退化为经典梁模型的平衡方程

(12)

对比式(11)与式(12)可知，微尺度梁模型的微分方程与经典梁模型的微分方程一致,只是在弯曲刚度中多了一项与尺度效应有关的项。同理，微尺度Kirchhoff板模型的微分方程与经典板模型的微分方程也一致。

3　有限元法

本文基于微尺度梁模型的微分方程与经典梁模型的微分方程一致，通过模量折算采用经典梁单元分析了微尺度模型的微观特性，这种方法简单、方便，非常适合工程应用。

由式(12)可知，经典梁模型的刚度仅由EI贡献；而由式(11)可知，欧拉微梁模型的刚度主要由EI和l2GA两项贡献，其中第一项为经典刚度，第二项是由尺度效应引起的增强项。模量折算策略即将由尺度效应引起的增强项折算到经典刚度中,模量折算公式可表示为

(13)

将式(13)代入式(11)，则折算后新模型的平衡方程为

(14)

该平衡微分方程与经典梁模型的平衡微分方程的形式完全相同，仅弹性模量不同。经典梁模型的平衡微分方程可通过有限元软件求解，故折算后的新微分方程亦可由现有有限元软件求解。该方法实现了仅用经典梁单元即可分析微尺度模型的微观特性，因而非常适合工程应用。同理，该方法可推广应用于分析微尺度Kirchhoff板模型。

4　算例

算例中我们首先检验了本文有限元法在弯曲分析中的精度，之后通过若干算例研究了各种边界条件下弯曲挠度、自振频率和屈曲载荷的尺度效应。为方便表达梁两端的边界条件，用C表示固支，F表示自由端，H表示简支。梁的初始几何参数和材料参数如表1所示。经模量折算后，由Radioss中的经典梁单元求解了算例中的弯曲挠度、自振频率和屈曲载荷。

表1　微尺度梁的材料特性

4.1精度验证

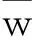
表2　微尺度各向同性梁在不同梁单元数下的弯曲挠度(l/h=1)

4.2不同边界条件下微尺度梁的弯曲分析

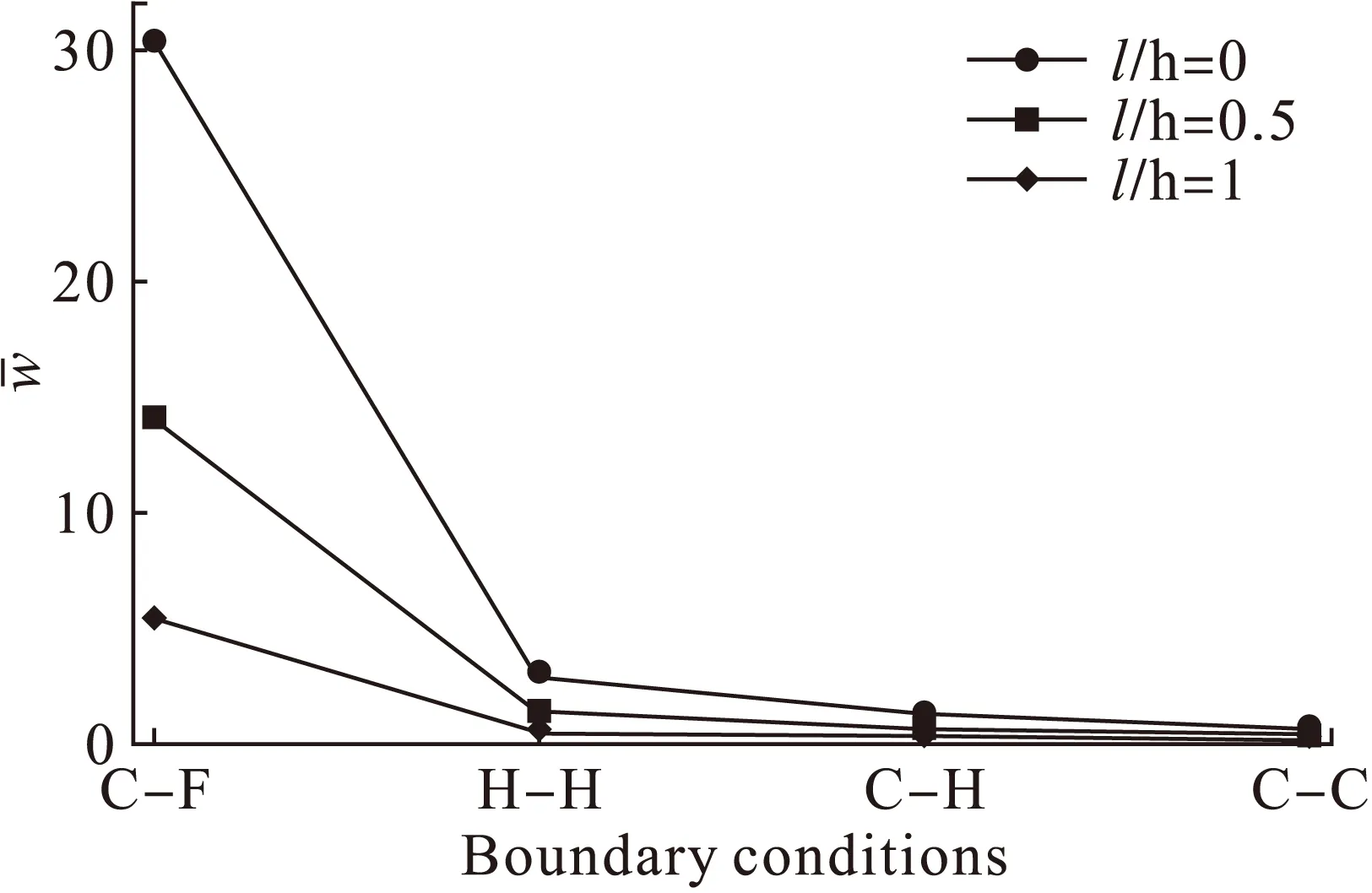
图2　不同边界条件下弯曲的尺度效应

图2给出了不同边界条件下微尺度梁的弯曲挠度。由图2可知，基于修正偶应力理论(l≠0)的微尺度梁的最大挠度随尺度参数的增加而减小，且均小于经典理论(l=0)的结果，这说明本文的弯曲模型捕捉到了尺度效应。另外，在同一尺度参数下，悬臂边界条件下的挠度远大于其它3种边界条件，因为悬臂边界条件下刚度最小。

4.3不同边界条件下微尺度梁的振动和稳定分析

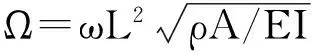
图3和图4给出了不同尺度参数下微尺度梁固支边界条件下的基频和屈曲载荷，横轴表示尺度参数，纵轴表示无量纲化后的基频和屈曲载荷。由图3和图4可知，微尺度梁的基频和屈曲载荷随尺度参数的增加而增加，且均大于经典理论的结果。而经典理论下的解是一个常数，不随尺度参数的变化而变化，这种现象同样存在于其它边界条件，这说明本文的振动和稳定模型能捕捉到尺度效应。另外，由表3可知，悬臂边界条件下的基频和屈曲载荷远小于其它3种边界条件，因为悬臂边界条件下其刚度最小。

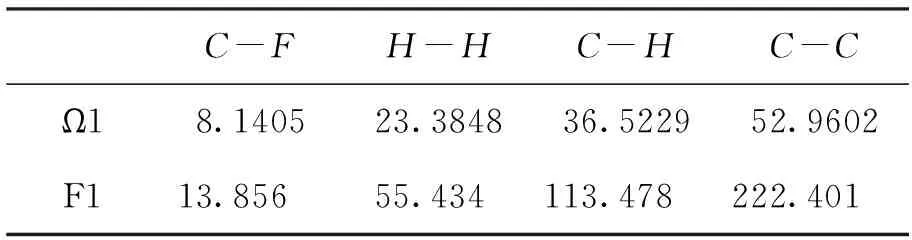
表3　不同边界条件下的基频和屈曲载荷 　(l=h)

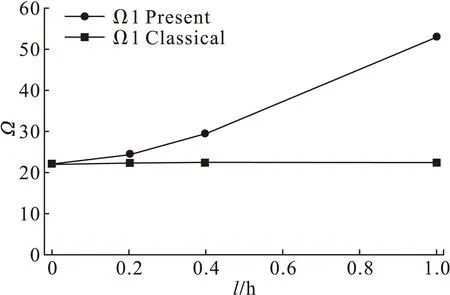
图3　固支边界下频率的尺度效应

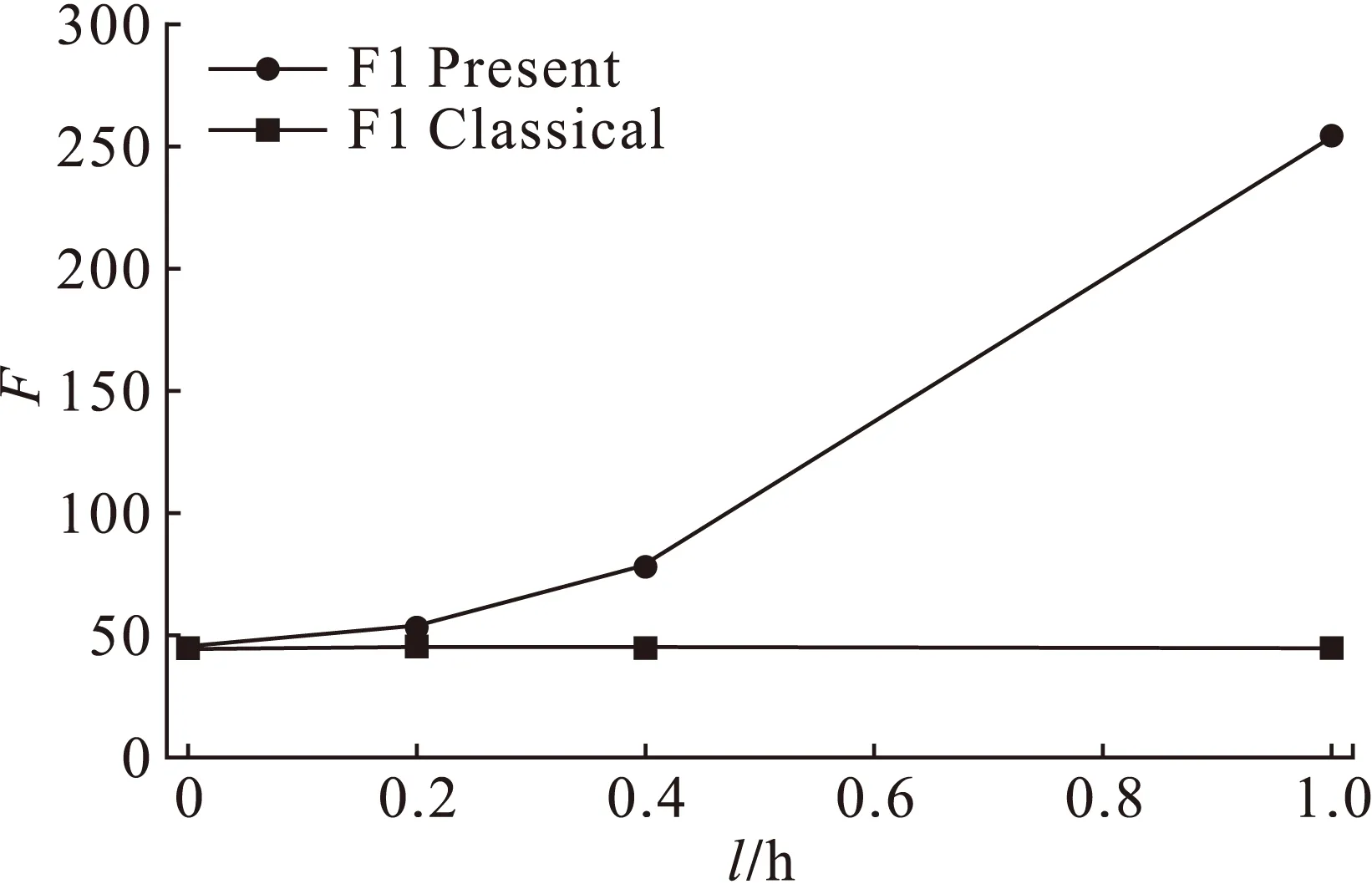
图4　固支边界下屈曲载荷的尺度效应

5　结论

本文基于修正偶应力理论建立了适用于任意边界条件的微尺度欧拉梁模型，非常适合工程应用。基于哈密顿原理推导了微尺度欧拉梁的平衡微分方程，其与经典梁的平衡微分方程具有相似的形式，仅在弯曲刚度中增加了与尺度效应有关的增强项；故本文提出模量折算策略，采用经典梁单元分析了微尺度欧拉梁弯曲挠度、基频和屈曲载荷的尺度效应。微尺度各向同性欧拉悬臂梁的弯曲挠度的有限元结果与现有文献的数值解吻合良好，证明了本文方法的合理性及精确性。算例结果表明，微细观尺度下梁结构将表现出比宏观状态下更强的抗弯刚度，即本文模型能捕捉到尺度效应，且当梁的几何尺寸与材料尺度参数越接近时材料尺度效应越明显；而当梁的几何尺寸远大于材料尺度参数时，材料的尺度效应消失，这说明材料的几何尺寸是影响尺度效应的决定性因素。进一步研究发现，梁模型弯曲挠度在悬臂边界条件下远大于其它边界条件，基频和屈曲载荷远小于其它边界条件。

[1]孙亮，王珺，韩平畴.单根聚己内酯电纺亚微米纤维的动力学特性分析[J].高分子学报,2009(6):535-539.

[2]LAMDCC,YANGF,CHONGACM,etal.Experimentsandtheoryinstraingradientelasticity[J].JournaloftheMechanicsandPhysicsofSolids,2003,51(8):1477-1508.

[3]KOUZELIM,MORTENSENA.Sizedependentstrengtheninginparticlereinforcedaluminium[J].ActaMaterialia,2002,50(1):39-51.

[4]FLECKNA,MULLERGM,ASHBYMF,etal.Straingradientplasticity:theoryandexperiment[J].ActaMetallurgicaetMaterialia,1994,42(2):475-487.

[5]LLOYDDJ.Particlereinforcedaluminiumandmagnesiummatrixcomposites[J].InternationalMaterialsReviews,1994,39(1):1-23.

[6]STELMASHENKONA,WALLSMG,BROWNLM,etal.MicroindentationsonWandMoorientedsinglecrystals:AnSTMstudy[J].ActaMetallurgicaetMaterialia,1993,41(10):2855-2865.

[7]KOITERW.Couple-stressesinthetheoryofelasticity[M].DictionaryGeotechnicalEngineering/WörterbuchGeotechnik，1964.

[8]MINDLINRD,TIERSTENHF.Effectsofcouple-stressesinlinearelasticity[J].ArchiveforRationalMechanics&Analysis,1962,11(1):415-448.

[9]MINDLINRD.Influenceofcouple-stressesonstressconcentrations[J].ExperimentalMechanics,1963,3(1):1-7.

[10]陈万吉，杨胜奇.有限元方法研究修正偶应力Mindlin层合板的尺寸效应[J].沈阳航空航天大学学报,2014,31(3):1-8.

[11]YANGF,CHONGACM,LAMDCC,etal.Couplestressbasedstraingradienttheoryforelasticity[J].InternationalJournalofSolidsandStructures，2002,39(10):2731-2743.

[12]CHENW,SIJ.Amodelofcompositelaminatedbeambasedontheglobal-localtheoryandnewmodifiedcouple-stresstheory[J].CompositeStructures，2013,103(0):99-107.

[13]陈万吉，郑楠.偶应力理论层合梁的稳定性及尺度效应[J].沈阳航空航天大学学报，2012,29(4):29-34.

[14]MAHM,GAOXL,REDDYJN.Anon-classicalMindlinplatemodelbasedonamodifiedcouplestresstheory[J].ActaMechanica，2011,220(1-4):217-235.

[15]ASGHARIM,RAHAEIFARDM,KAHROBAIYANMH,etal.ThemodifiedcouplestressfunctionallygradedTimoshenkobeamformulation[J].Materials&Design，2011,32(3):1435-1443.

[16]MAHM,GAOX,REDDYJN.Anonclassicalreddy-levinsonbeammodelbasedonamodifiedcouplestresstheory[J].InternationalJouranlforMultiscaleComputationalEngineering,2010,8(2):167-180.

[17]TSIATASGC.AnewKirchhoffplatemodelbasedonamodifiedcouplestresstheory[J].InternationalJournalofSolidsandStructures,2009,46(13):2757-2764.

[18]MAHM,GAOXL,REDDYJN.Amicrostructure-dependenttimoshenkobeammodelbasedonamodifiedcouplestresstheory[J].JournaloftheMechanicsandPhysicsofSolids,2008,56(12):3379-3391.

[19]PARKSK,GAOXL.Bernoulli-Eulerbeammodelbasedonamodifiedcouplestresstheory[J].JournalofMicromechanicsandMicroengineering,2006,16(11):2355.

[20]JOMEHZADEHE,NOORIHR,SAIDIAR.Thesize-dependentvibrationanalysisofmicro-platesbasedonamodifiedcouplestresstheory[J].PhysicaE:Low-dimensionalSystemsandNanostructures,2011,43(4):877-883.

[21]YINL,QIANQ,WANGL,etal.Vibrationanalysisofmicroscaleplatesbasedonmodifiedcouplestresstheory[J].ActaMechanicaSolidaSinica,2010,23(5):386-393.

(责任编辑：宋丽萍英文审校：赵欢)

Mechanical model and finite element analysis of Euler beam in a micro scale

HE Dan,CHEN Bo,YANG Wan-li

(Key Laboratory of Liaoning Province for Composite Structural Analysis of Aerocraft and Simulation,Shenyang Aerospace University,Shenyang 110136,China)

A model of micro Euler beam containing only one internal material length scale parameter and applieing to arbitrary boundary conditions was proposed based on the modified couple stress theory.Equilibrium differential equation of micro Euler beam was deduced using the Hamilton's principle,of which the form was similar to the classical model.The only difference was an additional term in bending rigidity associated with material length scale parameter.The equation could be used directly to analyze and explain multi-scale problems.Therefore,a strategy reducing modulus was proposed to solve the problems such as bending,vibration and buckling of micro beams by classical beam elements.The numerical results show that the bending rigidity of the Euler beam in a micro scale is higher than that in a macro scale,indicating that model presented in this paper can capture the scale effects.It is found that the geometric size is a significant factor of the scale effects.

modified couple stress theory;scale effects;finite element method;microbeam

2016-04-26

国家自然科学基金(项目编号：11572204)

贺丹(1979-)，男，辽宁沈阳人，博士，副教授，主要研究方向：微细观复合材料力学、结构优化，E-mail：Danhe@sau.edu.cn。

2095-1248(2016)04-0025-05

TU311

A

10.3969/j.issn.2095-1248.2016.04.005