自适应观测权重的目标跟踪算法*

刘　行，陈　莹

江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122

自适应观测权重的目标跟踪算法*

刘行，陈莹+

江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122

LIU Xing,CHEN Ying.Target tracking algorithm based on adaptive observation weight.Journal of Frontiers of Computer Science and Technology,2016,10(7)：1010-1020.

针对视觉跟踪在复杂场景中跟踪精度较低和鲁棒性较差的问题，在贝叶斯框架下提出了一种自适应观测权重的目标跟踪算法。通过视觉跟踪中的线性表示模型构建出一种加权观测模型；提出一种基于迭代加权的模型优化算法，利用在线更新的自适应权重矩阵消除观测离群值对跟踪有效性的影响；最后，采用有效的似然评估函数实现对目标准确、鲁棒的跟踪。实验结果表明，该算法在跟踪精度和鲁棒性方面都优于现有的一些跟踪算法。

视觉跟踪；线性表示；在线更新；离群值；自适应权重矩阵

1　引言

目标跟踪技术作为计算机视觉领域的重要课题已广泛运用于人机交互、视频监控、智能交通、航空航天等诸多领域。目前，虽然视觉跟踪领域已经产生一些比较优秀的跟踪算法[1-4]，但是在实际场景中由于存在光照变化、部分遮挡、低分辨率、目标形体变化及突然运动等诸多因素的干扰，设计出鲁棒、高效的跟踪算法仍然是一个具有挑战性的难题。

视觉跟踪领域已经提出的跟踪算法大体分为两类：判别式算法[5-7]和产生式算法[1,8-9]。判别式算法将目标跟踪看成一个二分类问题，从背景中区分出感兴趣的前景目标。产生式算法通过搜索与目标模型相似度最高的候选目标区域来进行跟踪。在产生式跟踪器中，基于线性表示模型的跟踪算法引起了广泛重视，出现了一些不错的跟踪算法[1,10-11]，其中最突出的算法是Ross等人提出的IVT（incremental visual tracking）跟踪器[1]。IVT在贝叶斯推理框架中通过PCA（principal component analysis）子空间对目标进行线性表示和在线增量学习的方式对子空间进行更新，取得了较好的跟踪效果，但由于IVT跟踪器将误差项看成是高斯分布的，构建出的模型对由部分遮挡、突然运动等干扰因素引起的离群值（离群值是指一组数据中与其他数值相比差异较大的数值）非常敏感，因此对于部分遮挡和突然运动等非常不鲁棒。为解决跟踪器对离群值的敏感性问题，Mei等人[12]利用目标模板和琐碎模板重构候选目标，提出了L1跟踪器，通过稀疏表示解决L1最小化问题去估计真实目标位置，但是存在L1最小化耗时非常严重的问题。Bao等人[13]提出了一种加速的近端梯度下降法进一步缓解L1最小化问题，但是在复杂场景中跟踪效果仍然不理想。Wang等人在文献[9]中提出了一种软阈值跟踪算法，将误差项看成是高斯-拉普拉斯分布，取得了一定的效果，但在具有众多干扰项的场景中仍存在跟踪精度较低和鲁棒性较差的问题。Wang等人[14]将正常值看成是高斯分布，离群值看成是均匀分布，提出了概率离群模型的跟踪算法，但这种对于离群值的处理仍然不够理想，还是会在一些复杂场景中出现跟踪漂移等问题。Xiao等人将L2范数用于视觉跟踪领域提出了L2跟踪器[15-16]，利用Square模板[17]去构建误差项，取得了一定的效果，但在强烈光照、部分遮挡等因素同时干扰时容易漂移和跟踪失败，并且鲁棒性较低。由于上述跟踪器大多将误差项看成是高斯分布或拉普拉斯分布，在没有众多干扰因素下是满足的，然而在实际中，特别是存在遮挡，目标突然运动等干扰时，误差项的分布是远离高斯或拉普拉斯分布的，就会对离群值非常敏感，造成跟踪算法失效。

针对当前跟踪算法对离群值敏感，导致在复杂场景中跟踪有效性和稳定性较低的问题，提出了一种自适应观测权重的目标跟踪算法（adaptive observation weighted tracking，AOWT）。算法未对观测误差作概率分布假设，而是通过重写误差项，利用线性表示模型[1]构建出一种加权观测模型，然后建立一种基于迭代加权的模型优化算法求解该模型，并且通过不断在线更新的自适应权重矩阵缓解并消除离群值对跟踪有效性的影响，进而建立似然评估函数精确、鲁棒地跟踪目标。

2　目标跟踪框架

视觉跟踪的两个核心部分就是运动模型和观测模型。本文在贝叶斯推理框架[1]下进行目标跟踪，跟踪框架流程图如图1所示。

图1中，首先由运动模型产生候选样本状态，然后通过观测模型评估运动模型产生的候选状态，得到最佳的候选状态后，通过增量PCA方法[1]更新观测模型，进行下一帧跟踪，最终实现对目标准确有效的跟踪。其中运动模型和观测模型的定义过程如下。

给定目标在第t帧的观测向量Zt={z1,z2,…,zn}，n是观测向量的维数，观测向量Zt是指在当前帧目标图像周围提取的候选目标图像块；,是第t帧目标的位置变量，其中xit表示第i个样本的位置状态。然后可以通过式（1）最大后验估计法得到最优的目标位置。

Fig.1　Flowchart of tracking framework图1　跟踪框架流程图

通过贝叶斯推理框架可以递归地求出后验概率p(Xt|Zt)，如式（2）所示：

式中，p(Xt|Xt-1)表示连续两帧之间的运动模型；p(Zt|Xt)是跟踪系统中的观测模型，也叫观测似然函数。

本文采用IVT[1]中6个仿射参数的方法来描述目标的运动模型，通过该模型产生候选样本状态，表示第i个样本在第t帧的目标状态量。其中是目标中心在x方向和y方向的平移量；表示旋转角；表示尺度变化量；表示高宽比；表示倾斜角。然后通过高斯分布来建模运动模型，如式（3）所示：

其中，N表示高斯分布；ψ是对角协方差矩阵，ψ中的元素由仿射参数的方差构成[1]。

观测模型在跟踪系统中有着重要的作用，往往对跟踪的有效性和鲁棒性有很大影响，本文提出一种加权观测模型来评估候选样本，得出最准确稳定的候选状态，利用增量PCA方法[1]更新观测模型，最终提出一种自适应观测权重的目标跟踪算法。

3　自适应观测权重的目标跟踪

首先通过问题分析提出本文的基本思想，然后具体介绍构建加权观测模型的过程，进而提出基于迭代加权的模型优化算法去求解观测模型。

3.1问题分析

由线性表示模型[1]可知，在第t帧目标的观测向量集Zt可以表示为：

上式就是通过A和βt对Zt进行编码。其中Zt是n维的观测向量；βt∈Rq×1是q维的编码系数向量；A=[a1,a2,…,aq]∈Rn×q是由若干帧跟踪结果构成的图像子空间的PCA基向量矩阵；e是编码误差项。

由于离群值像素通常发生在目标被遮挡或低分辨率的区域，相当于Zt中包含了离群值像素，而A仍然是根据前若干帧跟踪结果的图像子空间得到的，显然此时的编码误差e=Zt-Aβt会明显增大，如果不对离群值进行处理，就会造成编码的失效与不稳定，进而导致跟踪失败。目前大多数跟踪器[9,14,18-19]都将误差分布看成高斯或拉普拉斯分布构建出观测模型，这样的模型对跟踪过程中出现的离群值（通常是由遮挡、低分辨、突然运动等引起的）非常敏感。为了解决编码过程中对离群值敏感的问题，本文的基本思想是没有直接将误差项看成是高斯或拉普拉斯分布，而是通过重写误差项，建立一个与各数据点（像素点）有关的权重矩阵来构建出一种加权观测模型。该权重矩阵满足对编码误差大的点（离群值点）给予较小的权重，误差较小的点给予较大的权重（权重矩阵作用示意图如图2所示），然后提出一种基于迭代加权的模型优化算法，通过反复迭代以改进权重系数，消除离群值对编码有效性的影响，最终得到最佳的编码系数βt。

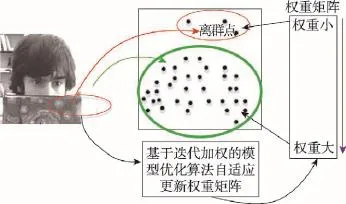
Fig.2　Weight matrix effect schematic图2　权重矩阵作用示意图

3.2加权观测模型

为了建立加权观测模型，可由式（4）重写误差项为：

其中，e的元素为ei=zi-aiβt,i=1,2,…,n。

假设e1,e2,…,en是独立同分布的，并且它们的概率密度函数为gθ(ei)，θ是表示特征分布的参数集，可得该估计量的似然函数如式（6）所示：

最大似然估计的目的是最大化式（6），等同于最小化式（7）：

通常情况下，可假设误差项的概率密度函数gθ(ei)是对称的，且当|ei|<|ej|时gθ(ei) ρθ(ej)。为了不失一般性，令ρθ(0)=0[20]。

其中，Gθ′(e0)是Gθ(e)的一阶导数Gθ′(e)在e0处的函数值，Gθ′(e0)=[ρθ′(e0,1);ρθ′(e0,2);…;ρθ′(e0,n)]，e0,i是e0的第i个元素；R1(e)是高阶残余项。

在编码过程中，为了使最小化更容易，一般要求Gθ(e)是凸函数，故这里可以将 R1(e)近似为 R1(e)≈(e-e0)W(e-e0)/2[20]。因为e中的元素是独立的，并且没有ei与ej(i≠j)的交叉项，所以W是一个对角矩阵。由 ρθ(ei)的性质可知，Gθ(e)在e=0时取得极小值，令Gθ′(0)=0可得W的对角元素Wi,i如式（10）所示：

由 ρθ(ei)的性质可知，ρθ′(e0,i)与e0,i有相同的符号，则Wi,i是大于0的标量。由文献[20]可知，式（9）可以被重写为式（11）：

b是和e0有关的一个常量，又因为e=Zt-Aβt，所以式（8）可以近似为式（12）：

其中，||⋅||2表示L2范数；W是一个对角矩阵，作用于测试图像的每一个像素。直观上，在跟踪过程中，为了缓解在编码Zt时由于部分遮挡、突然运动等造成的离群值像素对编码有效性的影响，此时应该给离群值像素赋予很小的权重值，即Wi,i的值很小，这样就会减少离群值对跟踪的影响。考虑到文献[21]中的logistic函数具有这样的性质，故可定义权重函数wθ(ei)：

其中，ε和γ是大于0的常量，ε控制从1到0的下降率，γ控制分界点的位置，当误差的平方大于γ时，权重值减小到0.5。

由3.1节的分析已经知道存在离群值像素的地方会导致编码误差ei过大，即当式（13）中的ei较大时，会使得exp(εγ-εei2)较小，从而导致式（13）的分母1+1/exp(εγ-εei2)较大，此时wθ(ei)就会取得较小值，因此该权重函数的定义保证了离群值像素处赋予小的权重值。同理，当编码误差ei偏小时，通过式（13）会赋予大的权重值，这样就保证了编码误差不同处的像素被赋予合适的权重值，达到了自适应更新观测权重的目的。在3.3节具体的优化算法中利用相邻迭代权重比的约束会进一步提高自适应能力。为了使跟踪对于离群值更加鲁棒，在实际算法中将ε 和γ都定义为与编码误差有关的常量，定义如下：

式中，Γa是Γ=[e12,e22,…,en2]经过升序排列之后得到的；h=ëλ2nû，λ2∈(0,1]，ëλ2nû表示取不超过λ2n的最大整数。定义ε的值为ε=λ3/γ，其中λ3是大于0的常量，本文取λ3=8。

3.3基于迭代加权的模型优化算法

3.3.1迭代加权模型优化算法的提出

本节通过基于迭代加权的模型优化算法求解观测模型，在迭代过程中通过式（13）来自适应更新权重矩阵W，消除离群值对跟踪有效性和鲁棒性的影响。直接采用L1-Ls[22]来计算式（12）非常耗时，因为式（12）是L1正则约束的最小化问题，由于L1正则化的目标函数在0处是不可导的，所以导致求解最小化比较复杂耗时。考虑到L2正则化的目标函数是一个二次函数，在0处是可导的，可以直接通过二次函数的导数为0来计算最小化问题，这样就会大大节省计算时间。又因为L2正则约束与L1相比唯一的区别是L2的稀疏性比L1要弱，在文献[23]中已经证明了稀疏性并不是影响编码效果的本质原因，并且利用L2范数代替L1范数进行编码求解取得与之前一样甚至更好的效果，因为L2范数能防止模型的过拟合问题。故式（12）可以通过L2正则约束来求解最小化问题（下文实验结果的定量分析中用AOWT（L1）表示利用L1-Ls来计算式（12）的AOWT算法，AOWT（L2）表示通过L2最小化来计算式（12）的AOWT算法），可设L2正则化二次函数为式（15）：

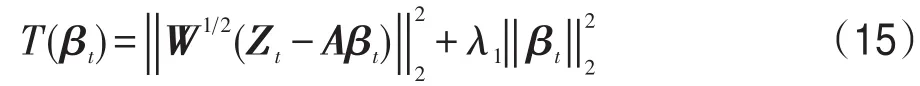
因为T(βt)是一个凸函数，所以令T(βt)的导数T′(βt)=0可以得到每次迭代最优的为：

基于迭代加权的模型优化算法流程如下所示。

算法1基于迭代加权的模型优化算法

输入：Zt，Zt_mean，A，其中Zt_mean为Zt的均值向量。

输出：βt。

（1）第一次迭代k=1，k表示迭代次数。

（2）计算误差e(k)=Zt-Zt(k)，且令Zt(1)=Zt_mean，其中Zt(k)表示第k次迭代的重构观测向量。

（3）计算第k次迭代的权重wθ(ei(k))：

其中ε(k)、γ(k)表示第k次迭代的ε和γ。

（7）重复步骤（2）～（6），直到连续5次迭代满足

或满足k=kmax。其中λ5是大于0任意小的常量，本文取λ5=0.01；kmax表示最大迭代次数，本文取kmax=10。

通过上述基于迭代加权的模型优化算法得到输出的βt，根据文献[12]可定义似然评估函数如式（20）所示：

最后采用增量PCA方法[1]对本文提出的AOWT跟踪器的观测模型进行在线更新。

3.3.2算法的收敛性分析

式（17）是式（8）的局部近似解，上述模型优化算法的每一次迭代都会使得式（8）的目标函数值减小，由于式（8）的非负稀疏约束，故随着迭代的不断进行，算法将会达到收敛[20]。

在具体优化算法中，如算法1中步骤（7）所示，当相邻迭代的权重差异比Rw连续5次迭代均小于一个大于0任意小的常量时，认为算法达到收敛，迭代停止。

3.3.3算法的复杂度分析

4　实验结果及性能分析

4.1实验装置与评价标准

实验仿真均在Matlab R2010b，Window8.1系统，Pentium®Dual-Core CPU处理器，3.20 GHz主频和4 GB内存的计算机环境下编程实现。为了验证本文算法的有效性，将本文提出的AOWT跟踪器与IVT跟踪器[1]、L2RLS跟踪器[16]、KCF跟踪器[3]、RPT跟踪器[24]在8个富有挑战性的视频序列中做了对比实验，AOWT与IVT、L2RLS采用的抽样粒子数均为600。

本文采用文献[25]中评估跟踪算法性能的两个重要指标，平均中心位置误差（average center location error，ACLE）和重叠精度（overlap precision，OP）来衡量跟踪算法的有效性。其中ACLE表示跟踪算法估计的目标中心位置与手动标记的ground-truth之间的平均欧式距离。OP表示跟踪算法标记的跟踪框与文献[25]中手动标记的跟踪框之间的重叠度SAOR超过一定阈值th(th∈[0,1])的帧数相对于视频序列总帧数的百分比（实验均采用与文献[24]中相同的阈值th=0.5）。重叠度的定义为：

其中，rt表示跟踪边界框的区域；rg表示ground-truth中标准跟踪边界框的区域；area表示求区域的面积。

4.2实验结果与分析

4.2.1定性分析

所有跟踪器的跟踪结果对比图如图3所示。本文提出的AOWT跟踪器的跟踪框采用红色实线标记，IVT跟踪器采用蓝色点划线标记，L2RLS跟踪器采用绿色虚线标记，KCF跟踪器采用黑色点线标记，RPT跟踪器采用黄色点划线标记但线宽比IVT的线宽粗。

（1）尺度变化和光照变化

在Singer1序列中，刚开始各算法都能较好跟踪，在98帧由于有着强烈的光照变化，除了AOWT跟踪器和L2RLS跟踪器能准确跟踪目标以外，其他跟踪器都已跟踪漂移，随着尺度的不断变化，最后只有AOWT能一直稳定跟踪目标。在DavidIndoorNew序列中，目标从黑暗的环境中慢慢走向光亮的地方，197帧时L2RLS跟踪器出现了轻微的跟踪漂移，其他算法均能较好跟踪，在496帧时，由于同时伴有尺度和摘戴眼镜等干扰，L2RLS出现很大程度的跟踪漂移，RPT尺度变化失败，最后只有AOWT、IVT、KCF能较准确地跟踪目标。在Caviar1中待跟踪目标渐渐地远离摄像机，尺度越来越小，可以看出KCF不能适应这样的尺度变化，到193帧时目标被其他行人遮挡，IVT出现跟踪漂移，最后只有AOWT和L2RLS能很好地处理目标的尺度变化，并保持有效的跟踪。

（2）严重遮挡和目标旋转

在Faceocc2序列中，在前几十帧的时候，各跟踪器都能基本保持良好跟踪，164帧中目标被书本遮挡，IVT出现了漂移，其他跟踪器都能准确跟踪，但到423帧时，目标被书本遮挡，同时伴随着头部旋转，只有AOWT仍能很好地适应旋转变化，其他算法都已跟踪漂移。在Caviar2序列中，刚开始待跟踪目标没有被其他行人遮挡时各算法均能较好跟踪，192帧时目标被遮挡，KCF和RPT出现了漂移，其他算法可以保持跟踪，到485帧时，L2RLS算法已经基本失效，IVT算法也错误跟踪到旁边的其他行人上，只有AOWT跟踪器仍能良好跟踪目标。在Caviar3序列中，开始的时候目标没有什么较大的干扰，各跟踪器都能比较准确地跟踪目标，71帧时当目标从左边走向右边，先是被穿红色衣服的行人严重遮挡，然后又被穿黑色衣服的行人遮挡，两次严重遮挡之后，只有AOWT算法能准确稳定地跟踪目标，其他算法都已经漂移甚至失败。

Fig.3　Tracking results comparison of different algorithms图3　各算法跟踪结果对比图

（3）运动模糊、形体变化和摄像机抖动

在Owl序列中，刚开始的时候没有出现摄像机抖动，待跟踪目标比较清晰，各跟踪器都能较好跟踪；到46帧时，由于严重的摄像机抖动导致目标变得很模糊，除了AOWT，其他算法都出现了不同程度的跟踪漂移现象；383帧时摄像机抖动得更加剧烈，目标严重模糊，此时其他跟踪器都已跟踪失败，只有本文提出的AOWT跟踪器仍能准确地跟踪，一直到最后，AOWT都保持着准确稳定的跟踪。在Face序列中，125帧时IVT和RPT出现跟踪漂移，伴随着摄像机长时间抖动，到305帧时KCF算法也偏移了目标，最后只有AOWT跟踪器和L2RLS跟踪器能较好地跟踪目标。

由以上可以看出，本文提出的AOWT跟踪器一直保持准确跟踪，而其他跟踪器大部分都会出现跟踪漂移，可见本文算法的性能优于其他算法。

4.2.2定量分析

（1）各算法的平均中心位置误差（ACLE）和重叠精度（OP）

如表1和表2所示，中心位置误差（center location error，CLE）曲线图如图4所示。其中，AOWT（L1）表示直接采用L1-Ls[22]工具包来计算式（12）的AOWT算法，AOWT（L2）表示利用L2最小化，通过式（17）来求解式（12）的AOWT算法。从表格和曲线图可以看出，AOWT算法在跟踪过程中平均中心位置误差小，重叠精度高，可见本文提出的AOWT算法在有效性和鲁棒性方面都优于其他算法。因为AOWT（L1）算法与AOWT（L2）算法唯一的区别仅仅在于计算式（12）的方法不同，所以它们的ACLE和OP基本差不多，主要体现在跟踪速度上的不同。

Table 1　Average center location error of different algorithms表1　跟踪算法的平均中心位置误差pixel

Table 2　Overlap precistion of different algorithms表2　跟踪算法的重叠精度

（2）跟踪速度分析

各跟踪器在不同视频序列中的跟踪速度如表3所示。首先从表3中可以明显看出，直接利用L1-Ls[22]工具包求解的AOWT算法（AOWT（L1））的跟踪速度比采用L2最小化求解的AOWT算法（AOWT（L2））的跟踪速度慢很多。另外，从表3中可见，KCF的速度最快，其次是IVT和AOWT（L2），KCF本身就是致力于高速的研究，利用循环结构通过离散傅里叶变换计算分类器的响应，减少了时间的消耗，但KCF的跟踪精度和鲁棒性明显不如本文提出的AOWT（L2）跟踪器。AOWT（L2）的跟踪速度比IVT慢一点，但跟踪精度却大大提升了，而其他算法的跟踪速度比AOWT（L2）都要慢。

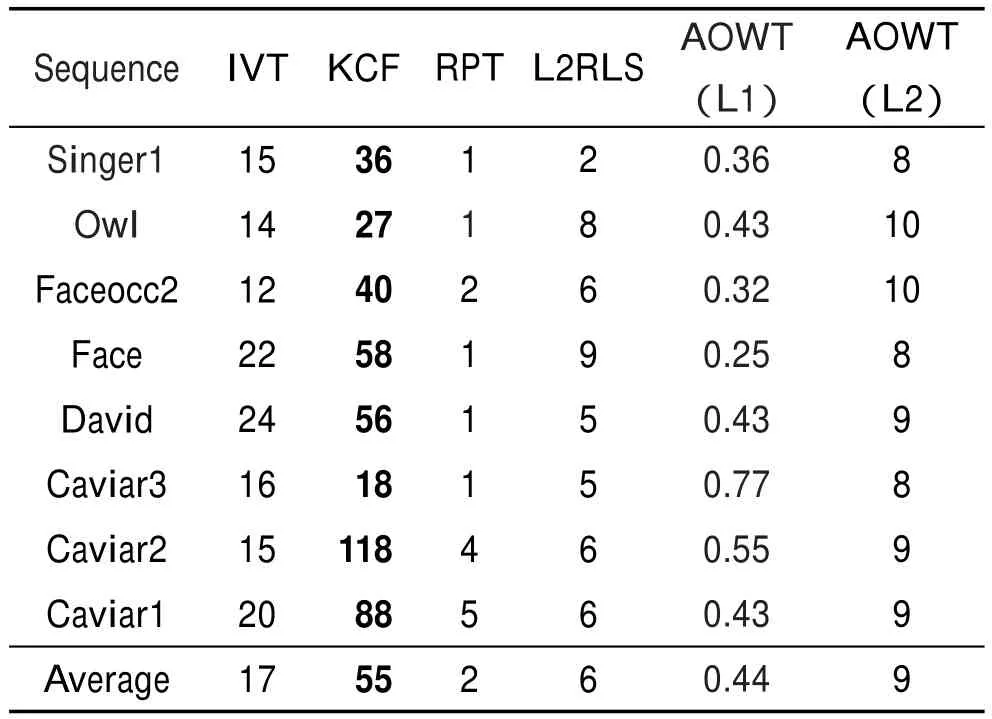
Table 3　Speed comparison of different trackers表3　各跟踪器的速度比较　f/s

Fig.4　Center location error of different algorithms图4　各算法的中心位置误差图

5　结束语

本文提出了一种自适应观测权重的目标跟踪算法，通过线性表示模型构建出一种加权观测模型；然后建立一种基于迭代加权的模型优化算法计算该模型，通过在线更新的自适应权重矩阵消除离群值对跟踪有效性的影响，最后建立似然评估函数实现对目标精确的跟踪。实验结果证明了AOWT跟踪器的有效性和鲁棒性。此外，本文算法仍然存在需要完善的地方，未来的工作主要致力于进一步提高观测模型的鲁棒性以及算法的优化问题，使得跟踪算法的精度更高，速度更快。

[1]Ross D A,Lim J,Lin R S,et al.Incremental learning for robust visual tracking[J].International Journal of Computer Vision,2008,77(1/3):125-141.

[2]Kalal Z,Mikolajczyk K,Matas J.Tracking-learning-detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(7):1409-1422.

[3]Henriques J F,Caseiro R,Martins P,et al.High-speed tracking with kernelized correlation filters[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2015,37(3): 583-596.

[4]Zhang Kaihua,Zhang Lei,Liu Qingshan,et al.Fast visual tracking via dense spatio-temporal context learning[M].[S.l.]: Springer International Publishing,2014:127-141.

[5]Grabner H,Bischof H.On-line boosting and vision[C]//Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,New York, USA,Jun 17-22,2006.Piscataway,USA:IEEE,2006,1:260-267.

[6]Henriques J F,Rui C,Martins P,et al.Exploiting the circulant structure of tracking-by-detection with kernels[C]// LNCS 7575:Proceedings of the 12th European Conference on Computer Vision,Florence,Italy,Octr 7-13,2012.Berlin,Heidelberg:Springer,2012:702-715.

[7]Hare S,Saffari A,Torr P H S.Struck:structured output tracking with kernels[C]//Proceedings of the 2011 IEEE International Conference on Computer Vision,Barcelona, Spain,Nov 6-13,2011.Piscataway,USA:IEEE,2011:263-270.

[8]Mei Xue,Ling Haibin.Robust visual tracking and vehicle classification via sparse representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011, 33(11):2259-2272.

[9]Wang Dong,Lu Huchuan,Yang M H.Least soft-threshold squares tracking[C]//Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition,Portland,USA,Jun 23-28,2013.Piscataway,USA:IEEE, 2013:2371-2378.

[10]Zhang Tianzhu,Ghanem B,Liu Si,et al.Robust visual tracking via multi-task sparse learning[C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition,Providence,USA,Jun 16-21,2012.Piscataway,USA:IEEE,2012:2042-2049.

[11]Wang Dong,Lu Huchuan,Yang M H.Online object tracking with sparse prototypes[J].IEEE Transactions on Image Processing,2013,22(1):314-325.

[12]Mei Xue,Ling Haibin.Robust visual tracking using ℓ1 minimization[C]//Proceedings of the 2009 IEEE 12th International Conference on Computer Vision,Kyoto,Japan,Sep 29-Oct 2,2009.Piscataway,USA:IEEE,2009:1436-1443.

[13]Bao Chenglong,Wu Yi,Ling Haibin,et al.Real time robust L1 tracker using accelerated proximal gradient approach [C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition,Providence,USA,Jun 16-21,2012.Piscataway,USA:IEEE,2012:1830-1837.

[14]Wang Dong,Lu Huchuan.Visual tracking via probability continuous outlier model[C]//Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus,USA,Jun 23-28,2014.Piscataway,USA:IEEE, 2014:3478-3485.

[15]Xiao Ziyang,Lu Huchuan,Wang Dong.Object tracking with L2-RLS[C]//Proceedings of the 2012 21st International Conference on Pattern Recognition,Tsukuba,Japan,Nov 11-15,2012.Piscataway,USA:IEEE,2012:1351-1354.

[16]Xiao Ziyang,Lu Huchuan,Wang Dong.L2-RLS-based object tracking[J].IEEE Transactions on Circuits and Systems for Video Technology,2014,24(8):1301-1309.

[17]Shi Qinfeng,Eriksson A,van den Hengel A,et al.Is face recognition really a compressive sensing problem?[C]//Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition,Providence,USA,Jun 20-25, 2011.Piscataway,USA:IEEE,2011:553-560.

[18]Li Xi,Hu Weiming,Zhang Zhongfei,et al.Visual trackingvia incremental log-Euclidean Riemannian subspace learning [C]//Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition,Anchorage,USA,Jun 23-28,2008.Piscataway,USA:IEEE,2008:1-8.

[19]Hu Weiming,Li Xi,Zhang Xiaoqin,et al.Incremental tensor subspace learning and its applications to foreground segmentation and tracking[J].International Journal of Computer Vision,2011,91(3):303-327.

[20]Yang Meng,Zhang Lei,Yang Jian,et al.Robust sparse coding for face recognition[C]//Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition,Providence,USA,Jun 20-25,2011.Piscataway,USA:IEEE,2011: 625-632.

[21]Zhang Jian,Jin Rong,Yang Yiming,et al.Modified logistic regression:an approximation to SVM and its applications in large-scale text categorization[C]//Proceedings of the 20th International Conference on Machine Learning,Washington,USA,Aug 21-24,2003:888-895.

[22]Kim S J,Koh K,Lustig M,et al.An interior-point method for large-scale l1-regularized least squares[J].IEEE Journal of Selected Topics in Signal Processing,2007,1(4):606-617.

[23]Zhang Lei,Yang Meng,Feng Xiangchu.Sparse representation or collaborative representation:which helps face recognition?[C]//Proceedings of the 2011 International Conference on Computer Vision,Barcelona,Spain,Nov 6-13,2011. Piscataway,USA:IEEE,2011:471-478.

[24]Li Yang,Zhu Jianke,Hoi S C H.Reliable patch trackers:robust visual tracking by exploiting reliable patches[C]//Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition,Boston,USA,Jun 7-12,2015.Piscataway,USA:IEEE,2015:353-361.

[25]Wu Yi,Lim J,Yang M H.Online object tracking:a benchmark[C]//Proceedings of the 2013 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Portland,USA,Jun 23-28,2013.Piscataway,USA:IEEE, 2013:2411-2418.

LIU Xing was born in 1990.He is an M.S.candidate at Jiangnan University.His research interest is visual target tracking.

刘行（1990—），男，安徽池州人，江南大学物联网工程学院硕士研究生，主要研究领域为视觉目标跟踪。

CHEN Ying was born in 1976.She received the Ph.D.degree from XiƳan Jiaotong University in 2005.Now she is a professor and M.S.supervisor at Jiangnan University,and the member of CCF.Her research interests include computer vision and pattern recognition.

陈莹（1976—），女，浙江丽水人，2005年于西安交通大学获得博士学位，现为江南大学物联网工程学院教授、硕士生导师，CCF会员，主要研究领域为计算机视觉，模式识别。

Target TrackingAlgorithm Based onAdaptive Observation Weight*

LIU Xing,CHEN Ying+
Key Laboratory of Advanced Process Control for Light Industry,Ministry of Education,Jiangnan University,Wuxi, Jiangsu 214122,China +Corresponding author:E-mail:chenying@jiangnan.edu.cn

To solve the problems of poor robustness and low effectiveness of visual tracking in complex scenes,this paper proposes a target tracking algorithm based on adaptive observation weight in Bayesian framework.Firstly,a weighted observation model is established via linear visual tracking representation.Then an iterative optimization algorithm is put forward to adaptively update the weight matrix to eliminate negative influences of observation outliers. Finally,effective likelihood evaluation function is adopted to capture the target accurately.The experimental results show that the proposed algorithm outperforms other state-of-the-art tracking algorithms in tracking accuracy and robustness.

visual tracking;linear representation;on-line updating;outliers;adaptive weight matrix

2015-10,Accepted 2015-12.

10.3778/j.issn.1673-9418.1510079

A

TP391

*The National Natural Science Foundation of China under Grant Nos.61104213,61573168(国家自然科学基金);the Prospective Joint Research Foundation of Jiangsu Province under Grant No.BY2015019-15(江苏省产学研前瞻性联合研究项目).

CNKI网络优先出版:2015-12-22,http://www.cnki.net/kcms/detail/11.5602.TP.20151222.1017.002.html