结合非空间属性的通用Skyline查询处理技术*
王海翔,郑吉平,2,3+,王永阁
1.南京航空航天大学 计算机科学与技术学院,南京 211106 2.南京大学 计算机软件新技术国家重点实验室,南京 210023 3.新南威尔士大学 计算机科学与工程学院,悉尼,澳大利亚 NSW 2052
结合非空间属性的通用Skyline查询处理技术*
王海翔1,郑吉平1,2,3+,王永阁1
1.南京航空航天大学 计算机科学与技术学院,南京 211106 2.南京大学 计算机软件新技术国家重点实验室,南京 210023 3.新南威尔士大学 计算机科学与工程学院,悉尼,澳大利亚 NSW 2052
WANG Haixiang,ZHENG Jiping,WANG Yongge.General Skyline query processing technology combining with non-spatial attributes.Journal of Frontiers of Computer Science and Technology,2016,10(7):936-947.
Skyline查询作为多目标决策的重要手段之一,近年来在各个领域得到广泛的应用。提出了结合非空间属性的通用Skyline查询处理技术,采用R树对设施集及数据集建立索引,并提出了两种方法来计算Skyline。第一种是基于全最近邻算法的扩展,通过计算静态Skyline结果来裁剪部分数据集。另一种是基于渐进最近邻的算法,采用查询点导向的搜索方法,利用静态Skyline结果计算与每一类设施最远的距离,将其作为边界阈值对数据点集进行裁剪,采用数据点导向的搜索方法,为裁剪后的每一个数据点计算距其最近的设施,并将数据点与设施的距离映射到多维距离空间中,结合非空间属性进行Skyline计算。实验结果表明,第二种方法减少了I/O次数,降低了CPU执行时间,提高了计算效率。
通用Skyline查询;R树索引;非空间属性;最近邻
1 引言
卫星成像技术、GPS定位技术和医学图像技术的发展促使了空间数据的产生,随着空间数据的增加,对其进行分析、处理、应用的需求也不断增大。此外,移动设备、无线通信技术的发展使得位置服务(location based services,LBS)在人们的日常生活中得到了广泛应用。Skyline查询作为多目标决策的重要手段之一,其在位置服务系统中也具有重要意义。
传统Skyline查询从给定数据集中返回不被其他点支配的点,然而实际应用中,可能还需要考虑其他因素的影响。例如,同学聚会时通常会选择交通方便的餐馆,因此会考虑离公交站台(假设只有一种交通工具)近的餐馆。然而除了聚餐,可能还有其他活动,如看电影,往往电影院和餐馆有一定的距离。这样就想找一个距离电影院、公交站台都很近的餐馆,但是电影院、公交站台又有很多个,并不能确定选择哪一个电影院、公交站台,这里针对某个餐馆,选择距其最近的公交站台和电影院作为距离的衡量标准。如图1(a)所示,在图中有一些公交站台、电影院和餐馆,如距离点p1最近的公交站台和电影院分别为b2和c2,然后将每个点映射到图1(b)的二维距离空间中,其中每个点的坐标含义是该餐馆与公交站台和电影院的最近距离,由此可得Skyline结果为{p1,p8}。对于这种类型的Skyline查询称之为通用Skyline查询(general Skyline queries)。此外,在选择餐馆时,可能并不仅仅关注距离这方面的属性,往往餐馆的非空间属性,如价格、评级、服务质量等也需要考虑在内,因此需要考虑结合非空间属性的查询。

Fig.1 Example of general Skyline queries图1 通用Skyline查询例子
此外,通用Skyline查询这类问题看成多源Skyline查询问题,对于多源Skyline查询已有一些研究,如文献[1-2]等,但这些研究中考虑的查询点是确定的,即在Skyline查询之前已确定了查询点的位置,因此可以利用一些空间几何的特性来处理这一类问题。但当查询点不确定时,首先需要确定查询点,然后才能进行Skyline查询。因为对于同类设施而言,不同的数据点对应的查询点可能是不同的,所以现有研究所采用的方法并不适用于这种查询。针对以上问题,本文提出了结合非空间属性的通用Skyline查询处理技术。
目前在多维数据查询的索引中,R树索引具有明显优势,并且本文设计的数据集均为多维数据集,为避免R树中节点的重叠区域过多,采用R树的变种R*树建立索引。因此,首先采用R树对设施集以及查询数据集建立索引来进行Skyline查询,进而提出基于全最近邻的Skyline查询算法及其扩展算法,以及基于渐进最近邻的Skyline查询算法。前者采用数据点导向搜索方法来为每一个数据点计算各类型设施中距离其最近的点,然后将该数据点与各类设施中点的距离映射到距离空间中,结合非空间属性并采用已有的Skyline查询处理方法进行Skyline的计算。因为静态Skyline结果不受距离支配的限制,仍然会属于最终Skyline,所以基于全近邻算法的扩展方法主要通过预先计算静态Skyline来减少数据集进行最近邻设施计算的个数,从而提高效率。后者采用查询点导向和数据点导向相结合的方法,首先计算静态Skyline结果,并计算其与各类设施距离的最大值作为阈值,每一类设施维护一个优先权队列,利用渐进最近邻的方法,使用阈值对数据集进行剪枝,对那些远于阈值的点进行裁剪,从而减少I/O以及各个数据点之间的支配性比较代价,提高计算效率。
2 相关工作
Borzsonyi等人[3]在数据库查询领域引入了Skyline操作后,研究人员在此基础上对集中数据库中的Skyline查询技术提出了许多改进方法[2,4-15]。
Sharifzadeh等人[1]首先介绍了空间Skyline的概念。假设P为数据点集合,Q为查询点集合,那么对Q而言,P的空间Skyline由P中没有被其他点所支配的点组成。提出了B2S(2branch-and-bound spatial Skyline)算法和VS(2Voronoi-based spatial Skyline)算法来计算空间Skyline结果。B2S2算法是在BBS(branchand-bound Skyline)算法的基础上提出的,使用R树为数据构建索引。VS2算法是基于Voronoi图的方法,主要思想是遍历Voronoi图对应的Delaunay图,在遍历过程中对图进行边界限定从而降低搜索空间。此外,还提出了VCS(2Voronoi-based continuous spatial Skyline query)算法对连续空间Skyline查询进行处理。Son等人[16]在上述研究的基础上对算法进行了改进。首先针对VS2算法不能完全返回正确的结果进行了验证,然后提出了一个新颖又有效的算法来进行空间Skyline查询。
文献[17-18]研究了单查询点移动的连续Skyline查询处理问题。Huang等人[17]利用时空相关性表示空间属性没有显著变化的两个时间片刻,通过维护事件来逐步求解Skyline结果。Cheema等人[18]提出使用安全区域(safe zone)的思想来减少属于最终空间Skyline的点的重复遍历。此外,Deng等人[2]提出了3个算法研究了公路网中的空间Skyline查询处理问题。Yoon等人[19]研究了无线传感器网络中的空间Skyline查询处理问题,用来进行多目标协同定位,提出了一个分布式的空间Skyline查询算法(distributed spatial Skyline,DSS)。DSS算法通过节点之间的几何属性以及拓扑结构来划分搜索空间,提供精确的结果。
现有的通用Skyline查询中[20]查询点是确定的,即在Skyline查询之前已确定了查询点的位置。但当查询点不确定时,首先需要确定查询点,然后才能进行Skyline查询。对于同类设施而言,不同的数据点对应的查询点可能是不同的,因此现有研究所采用的方法并不适用于这种查询。基于上述问题,本文提出了结合非空间属性的通用Skyline查询处理技术。
3 基于R树的最近邻方法
3.1问题定义
假设P表示数据点集合,F表示所有设施集合,Fi表示第i种类的设施集合,f表示某一个具体设施,设施种类共有m种。点p∈P与第i种设施的最近距离,使用p.di表示,也就是说p.di=min{Dist(p,f), f∈Fi}。如图1所示,共有公交站台和电影院两种设施,因此每个餐馆(数据点)可以映射到两维的空间中。假设点p共有d维非空间属性(非空间属性是指与距离无关的属性,例如餐馆的价格、评级、服务质量等),使用p.si表示点p的第i维非空间属性,使用D来表示维度集合。
那么结合非空间属性的通用Skyline查询定义如下(假设取小为优)。
定义1(静态支配)P中的两个点p和p′,如果对于∀i∈D,都有p.si≤p′.si,并且∃j∈D,使得p.sj 定义2(空间支配)P中的两个点p和p′,对于F来讲p空间支配p′,如果对于所有的类型i,都有p.di≤p′.di,并且存在一个设施类型 j,使得 p.dj< p′.dj成立,使用p≺spap′表示。 定义3(完全支配)如果将p与设施集合的最近距离映射到新的距离空间中,结合非空间属性,共有d+m维,使用D′来表示新的维度集合,使用p.vi表示新空间上的第i维的值。那么P中的两个点p和p′,如果对于∀i∈D′,都有p.vi≤p′.vi,并且∃j∈D′,使得p.vj 结合非空间属性的通用Skyline即由那些没有被任何点完全支配的点组成。 3.2R树与优先权队列 3.2.1R树 因为R树使用广泛,在处理多维数据查询时具有较高的效率,所以采用R树将空间数据建立索引,对m种设施的集合分别建立R树。采用优先权队列的方法对数据进行处理,获取第一个较优的点。 假设使用二维的数据构建R树,如图2所示R树的度为3。每一个中间记录ei表示每一个对应的下层节点的最小边界矩形(minimum bounding rectangle, MBR),叶子节点表示的是一个数据点。根据欧式距离来计算距离,也就是说,在进行最近邻计算时最小距离mindist的计算由式(1)确定,假设查询点为q的位置坐标为(q1,q1,…,qd): 数据点的mindist为查询点与数据点的欧式距离,MBR的mindist为查询点到该MBR的最小距离。 Fig.2 Example of R tree图2 R树举例 3.2.2优先权队列 将数据点建立R树索引后,在R树上进行查询处理,这里引入优先权队列(priority queue),按照某个函数保证队首元素始终是一个最优的元素。如果队首是一个数据点,那么取出的结果即为最优的结果;如果队首为一个中间记录e,那么将e取出,并按照e的孩子节点的key值插入到队列中。 定理1假设d(x,y)表示x与y的欧式距离,记录e为R树节点的最小边界矩形MBR,令q为查询点,那么对于子树Tsubtree的任意记录e,都有d(q,Tsubtree)≤d(q,e)。 证明 根据式(1),当Tsubtree只有一层,即其记录e对应R树的叶子节点为数据点,这时候d(q,Tsubtree)即为查询点q与记录e的距离,结论成立;当子树Tsubtree对应的记录为中间节点,利用反证法,假设d(q,Tsubtree)> d(q,e),d(q,Tsubtree)相当于查询点q与Tsubtree对应的MBR(使用MBRi表示)的最小距离,因为记录e为Tsubtree的记录,从而e在MBRi内,又d(q,Tsubtree)>d(q,e),所以查询点到MBRi的最小距离并不是d(q,Tsubtree),这与定义矛盾,因此d(q,Tsubtree)≤d(q,e),结论成立。□ 使用定理1,如果某一个记录e′与查询点的距离小于查询点与某子树的距离,即d(q,e) 3.3最近邻方法 3.3.1全最近邻算法 全最近邻(all nearest neighbor,ANN)算法从数据集中返回距离当前查询点最近的一个点,即将每个数据点作为查询点,查询距离该查询点最近的第i种类型的设施。将m种设施建立R*树索引,从而获取距离当前查询点p(某数据点)最近的m种设施f1,f2,…,fm,同时将 p与这些设施之间的距离映射到距离空间中,如图1(b)所示。 3.3.2渐进最近邻算法 渐进最近邻(incremental nearest neighbor,INN)算法是指逐步获取距离查询点q最近的数据点,即当已获得x个最近邻的点后,获取第x+1个距离查询点最近的点。假设使用R*树为所有的数据点建立索引,使用优先权队列Q来维护R*树的各个记录,其中距离查询点越近优先权越高。首先将R*树的根节点插入到队列中,在每一次INN查询时,都返回Q中最优的一个元素。若最优的元素是一个数据点,那么直接返回结果;若最优的元素是一个中间节点,则将其弹出,同时将其孩子节点放入Q中,直到找到第一个数据点。 ANN算法与INN算法最大的不同点是,ANN算法只返回距离查询点最近的一个数据点,而INN算法可以增量地返回距离查询点第i近的数据点。如图1所示,假设查询点位于原点,首先进行最近邻查询,然后进行INN查询,图3是优先权队列Q中的内容。首先将R树的根节点的所有记录插入到Q中,那么e6和e7进入队列,按照mindist排序,然后具有较小值的e7出队,其孩子节点的记录都插入到Q中。然后扩展e3,在得到p9后,ANN算法停止;而INN算法若继续执行会得到下一个距离查询点最近的数据点为p10,直到最后将所有的数据点都计算出来,INN算法输出的结果按照与查询点的距离依次递增。 Fig.3 Nearest neighbor queries图3 最近邻查询 3.4搜索导向 3.4.1数据点导向 对于每个数据点p,首先将p作为“查询点”,查询距离其最近的m种设施(查询点),如图1(a)所示,p1.dc和 p1.db可以使用最近邻的方法从Fc={c1,c2,c3}中和Fb={b1,b2}中选择,p1看作查询点。这种导向的优点是对于给定的数据点可以正确地返回距离其最近的设施点,并将其映射到距离空间上。然而这种方法需要对所有的数据点计算最近的距离,实际情况中并不是所有的数据点都需要用来计算Skyline结果,因此这种方法不能对数据集进行裁剪,当数据集较大时,对每个数据点进行最近邻查询,然后计算Skyline,开销较大。 3.4.2查询点导向 与上述方法不同,查询点导向的搜索将设施作为查询点来计算。使用静态Skyline结果来过滤掉一些不可能成为Skyline的点。这种方法可以对数据点集合进行裁剪,减少数据点的访问量。使用INN算法来逐步获得距离查询点最近的数据点,这里查询点是某一类型的设施。给出几个概念。 碰撞(hit):假设对某一设施 f∈F,维护一个半径fr,那么对于数据点 p而言,如果Dist(p,f)≤fr,则称p被 f碰撞。其中Dist(p,f)称为p与 f的碰撞距离,使用Distp,f表示。 对于每种设施类型i,维护一个全局的半径Ri, Ri表示对于i类型的设施而言当前最大的碰撞距离,由式(2)决定: 在每一次迭代中,对i类型的设施找一个新的设施点 f∈Fi来检测新的碰撞,这样Ri的增加是最小化的。如图4所示,第一次迭代计算距离b2最近的数据点,第二次迭代计算距离b1最近的数据点,将此时碰撞距离设置为Ri,因为此时Dist(b1,p7)>Dist(b2,p8)。因此Ri在搜索中是非递减的,根据其单调性,当数据点p被i类型的设施 f第一次碰撞时,可以设置为p.di=Distp,f,图4中第一次迭代可以计算出 p8.db和p1.dc。需要注意的是,一个数据点可能被相同类型的设施多次碰撞,这样的碰撞称为冗余碰撞,如图4中相对于c1的碰撞p1,因为它已经在第一次迭代中被c2碰撞。 根据以上分析,首先计算静态Skyline结果SKsta,然后计算SKsta中与每一种类型设施的最大距离,使用定理2对数据集进行裁剪。 定理2SKsta中的点距离i类设施的最远距离为di.max,i从1到m,对于任何一个点pt,如果对任意的i,i从1到m,pt与i类设施的最近距离大于等于di.max,那么pt不会属于最终Skyline。 证明 显然 pt∉SKsta,因此∃sp∈SKsta,使得sp能够静态支配pt。因为SKsta中的点距离i类设施的最远距离为di.max,所有sp距离i类设施的距离小于等于di.max。又因为pt与i类设施的最近距离大于等于di.max,所以有sp空间支配 pt。因此,pt被sp完全支配,其不属于SK。□ Fig.4 Query point oriented search图4 查询点导向的搜索 如图4所示,假设静态Skyline结果SKsta={p3,p8},这两个点距离c设施和b设施的最大距离分别为p3.dc和 p3.db。在第4次迭代过程后,获得了所有小于这两个阈值的碰撞,而那些尚未被任何一种设施碰撞过的点 p4、p5和 p6,因为其与c设施和b设施的最近距离都大于阈值,所以直接可以将p4、p5和p6裁剪,这些点不会属于最终Skyline结果。 除了可以对数据集进行裁剪,查询点导向的搜索的另一个好处是在INN查询中碰撞距离的计算代价较小。因为INN算法可以通过连续地维护优先权队列来分享计算,所以平均了计算代价。将在下一节讨论基于INN的Skyline查询处理算法。 4.1基于ANN的Skyline查询算法及其扩展算法 当所有的数据点都能够映射到距离空间中时,结合非空间属性,便可以采用已有的Skyline查询处理技术来处理问题。一种直接的方法是首先计算所有查询点与设施集合的最小距离,然后映射到距离空间中,之后再采用已有的Skyline算法来计算。这里采用前一节所述的全最近邻查询算法来计算数据点相对某种设施集合Fi的最近距离,称之为基于ANN的Skyline查询算法(Skyline query algorithm based on ANN,SQ_ANN),在不引起混淆的情况下简记为ANN。以下描述了基于ANN的Skyline查询算法。 算法1 SQ_ANN算法 1.For每个数据点p 2.for每一种设施集合Fi 3.使用ANN方法计算数据点p相对于Fi的最近距离p.di; 4.将p.di映射到距离空间上; 5.end for 6.end for 7.采用已有的Skyline查询算法来对距离空间上的数据以及非空间属性数据计算Skyline; 考虑到当静态Skyline结果较大时可以有效地减少进行全最近邻计算的数据点的个数,提出了基于ANN的Skyline查询的改进方法,称之为ex-ANN。可以先计算静态Skyline结果,然后将这部分结果放入Skyline结果,从而减少需要进行最近邻设施计算的数据集合大小。这种方法对于静态Skyline结果集较大时比较有效,因为通过计算SKsta便可以对数据集进行裁剪,并且SKsta肯定会成为最终Skyline结果,所以不需要对这部分数据进行全最近邻计算,从而节省了开销。 4.2基于INN的Skyline查询算法 尽管ex-ANN算法在静态Skyline结果集较大时可以很好地处理问题,但是多数情况下,静态Skyline结果与整个数据集比起来所占比例并不大。因此根据上一节讨论,结合数据点导向以及查询点导向的优缺点,将这两种搜索导向方法结合起来提出了一个高效的基于INN的Skyline查询算法(Skyline query algorithm based on INN,SQ_INN),在不引起混淆的情况下简记为INN。假设数据点集合使用R树建立索引,用RP表示,所有类型的设施集合也使用R树建立索引,假设i类型的设施使用RFi表示。 算法可以分成4个阶段,如下所示: 算法2 SQ_INN算法 //阶段1阈值计算 1.针对数据集的非空间属性计算静态Skyline结果SKsta; 2.for每一个pt∈SKsta 3.for每一种设施集合Fi 4.获取pt与设施集合最近邻的最远距离di.max; 5.end for //阶段2数据集裁剪 6.for每一种设施集合Fi 7.whileRi 8.p为相对Fi最近的数据点; 9.if对p的碰撞不是冗余碰撞 10.p.di=Ri,将p插入到候选集C中; 11.end while 12.end for //阶段3补全距离属性 13.for每一个pt∈C 14.for每一种设施集合Fi 15.ifpt.di未设置 16.计算pt相对于Fi的最近邻; 17.end for //阶段4 18.采用已有的Skyline查询算法来对距离空间上的数据计算Skyline; 阶段1对数据集的非空间属性计算静态Skyline结果SKsta,然后计算SKsta中与第i种类型设施最近邻的最大距离di.max,获取m个最大距离后作为阈值进入阶段2。 阶段2因为在实际应用中,查询点的个数往往远远少于数据点的个数,所以采用查询点导向的搜索方法来计算数据点的距离并且裁剪一些数据点,当到达阈值时,在该设施集合的搜索结束。为每一个设施 f维护一个优先权队列Qf来进行INN查询,为每一种类型的设施i维护一个优先权队列QFi来记录对于Fi而言最近的数据点,QFi中具有最小距离的元素具有最大的优先权。首先对Fi中所有的设施 f调用INN查询,获取QFi队首的数据点p,然后将其弹出队列,然后计算下一个距离最近的数据点p2,将其插入队列。如果当前的碰撞并非冗余碰撞,则,即数据点p相对i类设施的最近距离是当前的碰撞距离,此时的碰撞距离即Ri。当Ri≥di.max时,迭代结束,此时那些至少被碰撞过一次的数据点进入候选集,从而裁剪掉那些没有被碰撞过的点。 如图4所示,假设静态Skyline结果SKsta={p3,p8},这两个点距离c设施和b设施的最大距离分别为p3.dc和p3.db。第一轮迭代,对设施b,首先获得p8,p8的碰撞非冗余碰撞,因此设置 p8.db;对设施c,首先获得p1,因为其也非冗余碰撞,所以设置p1.dc,这两个点都插入到候选集中。第四轮迭代后,下一轮迭代Rc和Rb将会超过 p3.dc和 p3.db,因此迭代结束。这时没有被任何设施碰撞的点被裁剪掉,阶段2结束,此时候选集中C的点为{p1,p2,p3,p7,p8}。 阶段3对候选集中的数据点采用数据点导向的搜索方法进行距离计算。如在阶段2结束后,p1、p2和p7仅被一种设施类型碰撞,需要对这3个点进行相对其他设施类型的最近邻计算,从而获得p1.db、p2.db和p7.dc,当所有候选集中的数据点的距离都计算结束后,阶段3结束。 阶段4对候选集中映射到距离空间中的点结合非空间属性采用已有的Skyline查询算法来计算最终Skyline结果。 在实验中,利用生成的数据集对本文提出的基于ANN的Skyline查询算法及其扩展算法,以及基于INN的Skyline查询算法进行比较和分析。所有算法采用Visual C++2010实现,在3.3 GHz Intel Core i3-2120 CPU和3 GB内存系统上执行。 5.1实验设置 采用文献[3]中的方法生成空间属性和非空间属性独立分布、相关分布、反相关分布的合成数据集。针对数据点集合和设施集合,首先生成两维的独立分布数据作为各个集合中点的空间位置,数据各个维度的范围是[0,1],空间位置的范围是1×1。比较基于ANN的算法SQ_ANN及其扩展算法ex-ANN,以及基于INN的算法SQ_INN的执行效率,通过算法运行时间、I/O次数来比较算法的性能,同时比较了Skyline结果集合的大小。实验主要分析非空间属性维度、数据集大小、设施种类以及每种设施数量大小改变情况下的算法性能,表1为主要参数的默认值及其变化范围。采用R*树对数据集合和设施集合构建索引,索引构建数据页大小都设置为1 KB。 Table 1 Experiment parameters表1 实验参数 5.2实验结果 由于在进行结合非空间属性的通用Skyline查询时,主要的时间以及I/O消耗发生在最近邻计算阶段,在进行实验对比时,在数据点的非空间属性维度不变的情况下,非空间属性的数据分布相关、独立、反相关对算法的执行效率影响不大,因此只采用独立分布数据来进行实验比较。在进行非空间属性维度对算法性能影响的实验时,考虑了3种分布:相关分布、反相关分布、独立分布(静态属性值从0到1变化)对算法性能的影响。 实验通过比较执行时间、I/O次数对比了SQ_ANN算法、ex-ANN算法与SQ_INN算法的性能。同时比较了不同情况下Skyline结果的大小。实验表明,SQ_INN算法比SQ_ANN算法及其扩展算法无论在执行时间还是I/O代价上,在处理结合非空间属性的通用Skyline查询时都较优。 5.2.1非空间属性维度对算法性能的影响 图5~图7比较了在非空间属性维度变化的情况下对算法性能的影响,图中(a)、(b)和(c)分别表示非空间属性服从相关分布、反相关分布和独立分布。图5表示I/O次数,图6表示CPU执行时间,图7表示Skyline大小随着每种设施数量变化产生的影响。从图中可以看出,INN算法在各个方面要明显优于ANN及其扩展算法。从图5可以看出,随着非空间属性维度增大,I/O次数对于ANN和INN算法并没有明显影响。这主要是因为在进行全最近邻查询时,并不涉及非空间属性,所以其I/O消耗主要是进行最近邻查询时产生的。从图6可以看出,随着非空间属性维度增大,对于反相关分布,CPU执行时间都随之增加,这主要是因为非空间属性维度的增加使得两点之间的支配性代价增加,所以计算Skyline时产生了更多的时间消耗。从图7中可以看出,对于反相关分布和独立分布,静态Skyline的大小明显增加,因此ex-ANN算法要优于ANN算法。基于上述分析,随着维度增加,两两点间的支配性概率降低,非空间属性维度对最终Skyline结果影响较大。 Fig.5 I/O number on non-spatial dimension图5 非空间属性维度对I/O次数的影响 Fig.6 CPU time on non-spatial dimension图6 非空间属性维度对CPU执行时间的影响 Fig.7 Skyline set on non-spatial dimension图7 非空间属性维度对Skyline结果集的影响 5.2.2数据集合大小对算法性能的影响 图8比较了在数据集合大小变化的情况下对算法性能的影响,图中(a)、(b)和(c)分别表示I/O次数、CPU执行时间以及Skyline大小随着数据集大小变化产生的影响。从图中可以看出,INN算法在各个方面要明显优于ANN及其扩展算法。图8(a)和图8(b)表明,随着数据集增大,I/O次数和CPU执行时间都随之增加。这主要是因为对于ANN查询,随着数据集的增大,其对于每一种类型的设施进行最近邻查询时所消耗的I/O和CPU执行时间成正比,所以ANN算法所消耗的时间与I/O次数随着数据集增大明显增加。将距离映射到二维的距离空间中加上非空间属性进行Skyline计算。从图8(c)中可以看出,静态Skyline的大小与整个数据集相比,数量可以忽略,因此对于ex-ANN算法与ANN算法基本性能相等。 5.2.3设施的种类对算法性能的影响 图9比较了在设施种类变化的情况下对算法性能的影响,图中(a)、(b)和(c)分别表示I/O次数、CPU执行时间以及Skyline大小随着设施种类变化产生的影响。从图中可以看出,INN算法在各个方面要明显优于ANN及其扩展算法。图9(a)和图9(b)表明,随着数据集增大,I/O次数和CPU执行时间都随之增加。这主要是因为对于ANN查询,虽然数据集大小相同,但是相当于对n种设施都需要进行一次最近邻查询,I/O次数和CPU执行时间与设施种类成正比,所以ANN算法所消耗的时间与I/O次数随着设施种类增加明显增大。从图9(c)中可以看出,静态Skyline的大小与整个数据集相比,数量可以忽略,因此对于ex-ANN算法与ANN算法基本性能相等。将距离映射到n维的距离空间中加上非空间属性进行Skyline计算,Skyline结果大小随着设施种类的增加显著增大。这主要是因为随着维度的增加,各个点之间被支配的概率降低,所以Skyline结果集也随之增加。 Fig.8 Algorithm performance with different sizes of datasets图8 数据集大小对算法性能的影响 Fig.9 Algorithm performance with different kinds of facilities图9 设施种类对算法性能的影响 5.2.4每种设施数量对算法性能的影响 图10比较了在每种设施数量变化的情况下对算法性能的影响,图中(a)、(b)和(c)分别表示I/O次数、CPU执行时间以及Skyline大小随着每种设施数量变化产生的影响。从图中可以看出,INN算法在各个方面要明显优于ANN及其扩展算法。图10(a)和图10(b)表明,随着每种设施数量增大,I/O次数和CPU执行时间都随之增加,这主要是因为对于ANN查询,每种设施种类增加,所以对于设施集合所建立的R树节点个数也会有所增加,在进行最近邻查询的时候,对设施进行一次最近邻查询所消耗的I/O次数和CPU执行时间增加,当数据集合大小不变,设施种类不变时,总的I/O次数与执行时间随之变大。因此ANN算法所消耗的时间与I/O次数随着设施种类增加明显增大。从图10(c)中可以看出,静态Skyline的大小与整个数据集相比,数量可以忽略,因此对于ex-ANN算法与ANN算法基本性能相等。每种设施数量并不影响最终Skyline的计算,因此对Skyline结果大小也没有明显影响。 Fig.10 Algorithm performance with different numbers of facilities图10 每种设施数量对算法性能的影响 本文研究了结合非空间属性的通用Skyline查询处理技术,从设施集合中选择距离某数据点最近的设施,并将其与该数据点之间的距离映射到距离空间上,然后在新的距离空间中进行Skyline查询。采用R树索引结构对数据集建立索引,根据数据点导向和查询点导向两种不同的搜索导向的优缺点,提出了SQ_ANN算法及其扩展算法,以及SQ_INN算法。SQ_INN算法主要是通过过滤的方法来对数据集进行剪枝,减少I/O次数。理论和实验表明SQ_INN算法无论在CPU执行时间还是I/O次数上都优于SQ_ANN算法。 [1]Sharifzadeh M,Shahabi C.The spatial skyline queries[C]// Proceedings of the 32nd International Conference on Very Large Data Bases,Seoul,Korea,Sep 12-15,2006:751-762. [2]Deng Ke,Zhou Xiaofang,Shen Hengtao.Multi-source skyline query processing in road networks[C]//Proceedings of the 23rd IEEE International Conference on Data Engineering,Istanbul,Turkey,Apr 15-20,2007.Piscataway,USA: IEEE,2007:796-805. [3]Borzsonyi S,Kossmann D,Stocker K.The skyline operator [C]//Proceedings of the 17th International Conference on Data Engineering,Heidelberg,Germany,Apr 2-6,2001.Piscataway, USA:IEEE,2001:421-430. [4]Tan K L,Eng P K,Ooi B C.Efficient progressive skyline computation[C]//Proceedings of the 27th International Conference on Very Large Data Bases,Roma,Italy,Sep 11-14, 2001:301-310. [5]Chomicki J,Godfrey P,Gryz J,et al.Skyline with presorting [C]//Proceedings of the 19th International Conference on Data Engineering,Bangalore,India,Mar 5-8,2003.Piscataway,USA:IEEE,2003:717-719. [6]Godfrey P,Shipley R,Gryz J.Maximal vector computation in large data sets[C]//Proceedings of the 31st International Conference on Very Large Data Bases,Trondheim,Norway, Aug 30-Sep 2,2005:229-240. [7]Kossmann D,Ramsak F,Rost S.Shooting stars in the sky:an online algorithm for skyline queries[C]//Proceedings of the 28th International Conference on Very Large Data Bases, HongKong,China,Aug 20-23,2002:275-286. [8]Papadias D,Tao Yufei,Fu G,et al.Progressive skyline computation in database systems[J].ACM Transactions on Database Systems,2005,30(1):41-82. [9]Papadias D,Tao Yufei,Fu G,et al.An optimal and progressive algorithm for skyline queries[C]//Proceedings of the2003 ACM SIGMOD International Conference on Management of Data,San Diego,USA,Jun 9-12,2003.New York, USA:ACM,2003:467-478. [10]Wu Ping,Zhang Caijie,Feng Ying,et al.Parallelizing skyline queries for scalable distribution[C]//LNCS 3896:Proceedings of the 10th International Conference on Extending Database Technology,Munich,Germany,Mar 26-31,2006. Berlin,Heidelberg:Springer,2006:112-130. [11]Chen Lijiang,Cui Bin,Lu Hua,et al.iSky:efficient and progressive skyline computing in a structured P2P network [C]//Proceedings of the 28th International Conference on Distributed Computing Systems,Beijing,China,Jun 17-20, 2008.Piscataway,USA:IEEE,2008:160-167. [12]Tao Yufei,Papadias D.Maintaining sliding window skylines on data streams[J].IEEE Transactions on Knowledge and Data Engineering,2006,18(3):377-391. [13]Pei Jian,Jiang Bin,Lin Xuemin,et al.Probabilistic skylines on uncertain data[C]//Proceedings of the 33rd International Conference on Very Large Data Bases,Vienna,Austria,Sep 23-27,2007:15-26. [14]Yoon K,Chung Y D,SangKeun L E E.In-network processing for skyline queries in sensor networks[J].IEICE Transactions on Communications,2007,90(12):3452-3459. [15]Su I F,Chung Y C,Lee C,et al.Efficient skyline query processing in wireless sensor networks[J].Journal of Parallel and Distributed Computing,2010,70(6):680-698. [16]Son W,Lee M W,Ahn H K,et al.Spatial skyline queries: an efficient geometric algorithm[C]//LNCS 5644:Proceedings of the 11th International Symposium on Spatial and Temporal Databases,Aalborg,Denmark,Jul 8-10,2009.Berlin,Heidelberg:Springer,2009:247-264. [17]Huang Zhiyong,Lu Hua,Ooi B C,et al.Continuous skyline queries for moving objects[J].IEEE Transactions on Knowledge and Data Engineering,2006,18(12):1645-1658. [18]Cheema M A,Lin Xuemin,Zhang Wenjie,et al.A safe zone based approach for monitoring moving skyline queries [C]//Proceedings of the 16th International Conference on Extending Database Technology,Genoa,Italy,Mar 18-22, 2013.New York,USA:ACM,2013:275-286. [19]Yoon S H,Shahabi C.Distributed spatial skyline query processing in wireless sensor networks[C]//Proceedings of the International Workshop on Sensor Webs,Databases,and Mining in Networked Sensing Systems in Conjunction with International Conference on Networked Sensing Systems, 2009. [20]Lin Qianlu,Zhang Ying,Zhang Wenjie,et al.Efficient general spatial skyline computation[J].World Wide Web,2013, 16(3):247-270. WANG Haixiang was born in 1989.She received the M.S.degree from Nanjing University of Aeronautics and Astronautics in 2015.Her research interests include Skyline computation and perceptive data management,etc. 王海翔(1989—),女,江苏连云港人,2015年于南京航空航天大学获得硕士学位,主要研究领域为Skyline计算,感知数据管理等。 ZHENG Jiping was born in 1979.He received the Ph.D.degree from Nanjing University of Aeronautics and Astronautics in 2007.From 2007 to 2009,he was a post-doctoral researcher at Department of Computer Science of Tsinghua University.From 2016 to 2017,he is a CSC visiting scholar at School of Computer Science and Engineering of University of New South Wales.Now he is an associate professor at Nanjing University of Aeronautics and Astronautics,and the senior member of CCF.His research interests include Skyline computation,perceptive data management,computational geometry and Monte Carlo methods,etc. 郑吉平(1979—),男,江苏南京人,2007年于南京航空航天大学获得工学博士学位,2007—2009年在清华大学计算机系从事博士后研究工作,2016—2017年在澳大利亚新南威尔士大学计算机科学与工程学院从事国家公派访问学者工作,现为南京航空航天大学副教授,CCF高级会员,主要研究领域为Skyline计算,感知数据管理,计算几何,蒙特卡罗方法等。 WANG Yongge was born in 1989.He is an M.S.candidate at Nanjing University of Aeronautics and Astronautics. His research interests include probabilistic Skyline computation and perceptive data management,etc. 王永阁(1989—),男,江苏徐州人,南京航空航天大学硕士研究生,主要研究领域为概率Skyline计算,感知数据管理等。 General Skyline Query Processing Technology Combiningwith Non-spatial Attributesƽ WANG Haixiang1,ZHENG Jiping1,2,3+,WANG Yongge1 As one of the important methods for multi-criteria decision making problems,the Skyline query processing technologies have been widely studied in many applications.This paper proposes the general Skyline query processing technology combining with non-spatial attributes while R tree is adopted to index the facility set and the dataset.Two algorithms are provided to compute the Skyline results.The first algorithm is the extension of Skyline query algorithm based on all nearest neighbor method,which cuts off part of the dataset by computing the static Skyline results.The second algorithm is based on incremental nearest neighbor method,which utilizes the facility oriented searching method. The algorithm calculates the farthest distances between the static Skyline results and each type of facilities.The distances are set to bound thresholds so as to cut off data points which are farther than them.For the left points,data ori-ented search method is used to compute the nearest facilities of all types.After that,the distances between the data points and the facilities are mapped to the multi-dimensional distance space so as to compute the Skyline result combining with non-spatial attributes.The experimental results show that for the second algorithm the number of I/Os and CPU time are greatly reduced thus improves the computational efficiency. general Skyline queries;R-tree index;non-spatial attributes;nearest neighbor 2015-06,Accepted 2015-10. 10.3778/j.issn.1673-9418.1506091 A TP392 *The Natural Science Foundation of Jiangsu Province under Grant No.BK2014086(江苏省自然科学基金);the Fundamental Research Funds for the Central Universities of China under Grant No.NS2015095(中央高校基本科研业务费专项资金);the Foundation of Graduate Innovation Center in NUAAunder Grant No.KFJJ201461(南京航空航天大学研究生创新基地开放基金). CNKI网络优先出版:2015-10-20,http://www.cnki.net/kcms/detail/11.5602.TP.20151020.1042.018.html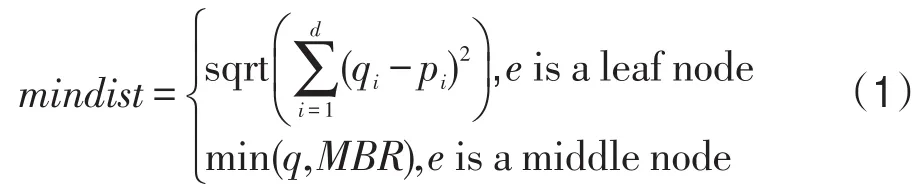




4 基于最近邻的Skyline查询算法
5 实验测评







6 总结



1.College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China 2.State Key Laboratory for Novel Software Technology,Nanjing University,Nanjing 210023,China 3.School of Computer Science and Engineering,University of New South Wales,Sydney,NSW 2052,Australia +Corresponding author:E-mail:zhjcs@nuaa.edu.cn

