一种缺失值填充方法的研究

韩榕生　刘志红

(华北电力大学 数理学院，北京 昌平 102206)



一种缺失值填充方法的研究

韩榕生刘志红

(华北电力大学 数理学院，北京 昌平 102206)

随着信息时代的到来，人们在各行各业都面临着海量的数据信息，而缺失数据的存在已成为人们对数据处理分析的一个重大难题。鉴于此，基于自联想神经网络方法，采用逆非线性主成分分析预测模型对宿州市天然气用量的原始数据构建缺失值填充模型。为进一步改进逆非线性主成分分析(Inverse Nonlinear principal component analysis model)方法出现的局部极小点和收敛速度慢的问题，采用共轭梯度算法对其进一步优化。

逆非线性主成分分析模型；共轭梯度法；预测模型

0　引言

无论是在科研实验，还是在银行、保险、金融投资以及社会调查等领域，我们收集到的数据常常是不完整数据。比如在处理影像恢复的物理问题时，由于各种因素影响，无法避免图像的降质，一些重要信息无法从影像中获取。这就需要我们对图像进行复原处理。另外在医学研究中，对病人临床试验时需要搜集大量的资料，有些病人可能不愿意接受调查或者不愿意反馈治疗效果等其他原因都会造成某些数据缺失的情况,从而增加科研等一系列工作统计分析的难度。因此对缺失值进行深入的研究具有重要意义。

从人们开始着手研究缺失数据的处理到现在，已取得了很多研究成果，总结了一些处理方法，并且在实际的应用中也产生了一定的经济效益[1—4]。A.P.Dempster等在1977年总结出了对缺失值填充的期望极大化(Expectation Maximization，简写为EM)算法[5],EM算法的出现加快了缺失数据填充的步伐，但是EM算法的收敛速度慢，计算较为复杂。之后，一些研究者相继提出了回归方法、贝叶斯方法以及多值填充方法。然而伴随着机器学习与数据挖掘的逐渐发展，缺失值填充的问题被进一步地补充。人工神经网络(Artificial Neural Networks，简写为ANN)是机器学习的一个庞大的分支，有几百种不同的算法。它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型，依靠着系统的复杂程度，通过调整网络相互连接的节点的关系，从而实现对信息的处理。神经网络具有自学习和自适应的能力，既可以实现聚类，也能够实现回归系统本身，这就为缺失值填充问题的研究又开拓了新的领域。

本文是基于Kramer[6]提出的一种自联想神经网络(Autoassociative Neural Networks，AANN)的非线性主成分方法，采用逆非线性主成分分析模型[7]对宿州市天然气用量进行分析预测。考虑到传统的神经的误差函数是以一个signmoid函数为自变量的非线性函数，因此由其构成的连接神经网络的权值不是只有一个极小的抛物面，而是存在多个极小超曲面。一旦网络在训练的过程中遇到局部极小点时或者在初始状态连接神经网络的权值过大，致使一开始网络就处于signmoid的饱和区域，这都将造成结果的不准确。为此本文采用共轭梯度法来减小震荡趋势，提高训练速度，加快网络的收敛。

1　基于自联想网络的非线性主成分提取

主成分分析方法是对原有的数据进行线组合，从而实现主成分的提取，在许多领域中都被广泛地应用。有些时候主成分与原有的数据呈现一种非线性的映射关系，若继续采用主成分分析的方法，必将使提取的主成分不准确。1991年Kramer[6]提出的自联想神经网络的非线性主成分算法，其基本原理如图1所示。

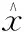
自联想神经网络模型包括输出模型、作用函数模型以及误差计算模型。

1.1自联想神经网络输出模型

映射层第k个神经元的输出为：

(1)

输出层第i个神经元的输出为：

(2)

1.2作用函数模型

神经元的激活函数是神经网络的重要组成部分，激活函数又包括多种类型，本文采用S形激活函数，即：

(3)

S型激活函数可将任意值压缩到(0，1)的范围内，是一个非线性型函数。

1.3误差计算模型

(4)

1.4INVERSE NLPCA MODEL

为进一步提高神经网络的计算效率，本文采用INVERSE NLPCA MODEL[7]，即自联想神经网络的解压缩网络过程。相比训练整个神经网络，逆模型的训练过程进一步地减少计算量，提高了计算效率，并且逆模型同样可以解决预测问题。相比之下，逆模型网络中不需要数据信息的输入，即可以任意给出瓶颈层的主成分(或者通过自联想神经网络的一次压缩过程获得主成分)，通过逆模型解压数据信息得到输出数据

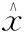
(5)

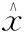
(6)

其中d代表样本数据的某性质，N代表样本数目，通过误差函数来修正逆模型网络的权重和瓶颈层的主成分以获得最小误差，从而实现对原样本数据缺失值的填充。其权值的梯度公式为：

(7)

(8)

相比较训练整个自联想神经网络，缩短了填充时间。考虑到INVERSE NLPCA MODEL方法的误差函数是一个以sigmoid函数为自变量的非线性函数，因此构成连接权值的空间存在一些局部极小面，在网络的训练的过程中，容易使网络陷入局部极小值。当误差函数接近极小点时，搜索步长会变得越来越小，导致收敛速度越来越慢。为进一步改进INVERSE NLPCA MODEL出现的局部极小点和收敛速度慢的问题，本文采用共轭梯度算法对其进一步优化。共轭梯度算法通过一次求导获得负梯度方向，然后按照与负梯度共轭的方向搜索，从而实现快速达到最优值。这样既克服了最速下降法的锯齿现象，又避免了牛顿法的计算量大和局部收敛性的缺点。

1.5基于共轭修梯度法对逆网络模型的修正可以归纳为：

(1)设初始权值为w，精度要求为，令n=n+1；

(3)否则，令d1=-g1，设λ为控制步长的参数，调节λ使得E(w1+λd1)到达最小值，并计算w2=w1+λmind1，检查是否满足停止条件；

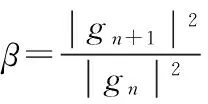
(5)令n=n+1,返回(6)。

2　填充结果与分析

为了检验INVERSE NLPCA MODEL填补缺失数据的性能，本文选取宿州市2010—2015年天然气用量及相关因素作为样本[8]，包括天然气用量人数、交通运输数量、工业天然气用量、餐饮业天然气用量、其他行业天然气用量和天然气总用量六大部分(详见表1)。测速变量为天然气总用量，在这些数据中随机删除某一年的天然气总用量和某一方面的天然气用量数据得到测试数据，用预测值比较删除的真实值。

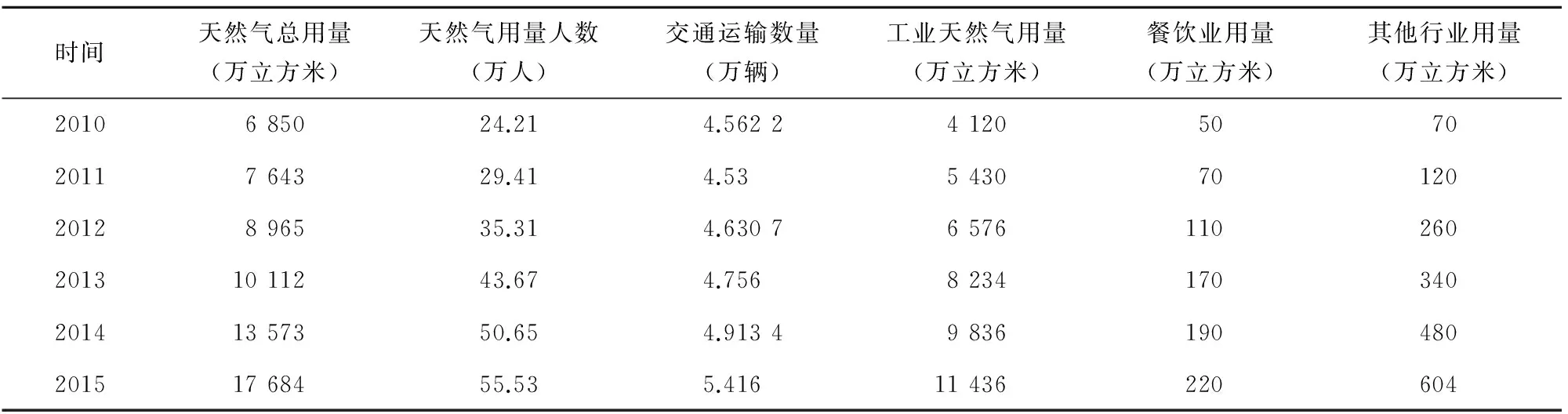
表1　天然气用量及相关因素的样本数据

本文采用fortran语言程序通过INVERSE NLPCA MODEL仿真，根据天然气用量及其相关因素把数据分为六部分，数据以矩阵的形式输入，矩阵的每一行对应一个观测事件，矩阵的每一列作为相应的属性。对2010—2015年天然气总用量的缺失值填充结果如表2所示。

表2中给出了原始值和填充值，并计算了相对误差以及平均相对误差。填充结果的相对误差和绝对误差均小于2%，说明该方法能够实现较为合理的缺失值填充。

表2　填充值及相对误差

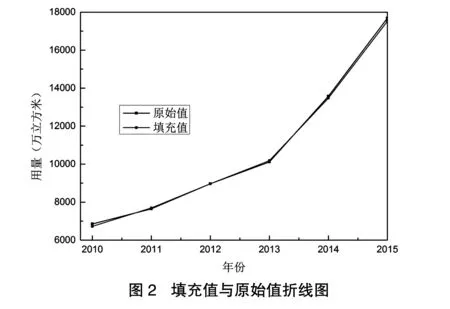
从图2我们可以看到，原始值和填充值吻合得比较好，进一步验证了该模型的可行性。

3　结论

本文针对天然气用量的缺失数据通过INVERSE NLPCA MODEL予以一定的填充，结果显示该模型能够很好解决缺失值填充的问题，并依据该模型可以得到较高的填充精度。因此，逆非线性主成分分析模型解决缺失值问题是简单可行并且有效的。本文给出的数据较少，缺失值数据也只占到15%到20%，考虑到该模型能够实现一个非线性问题的计算且能够将高维数据压缩到低维数据，我们也会进一步研究将该模型应用到高维大数据中去解决缺失值填充问题。

[1]Batista G E,Menards M C. A study of k-nearest neighbor as a model-based to treat missing data[J].Proeeedings of the Argentine Symposium on Artificial Intelligence,2003,(30):1—9.

[2]Gediga G,Duntsch I.Maximum Consistency of Incomplete Data via Non-Imputation[J].In Artificial Intelligence Review, 2003,19(1):93—107.

[3]Scheffer J.Dealing with Missing data[J].Research Letters in the Information and Mathematical Sciences, 2002,(2)：153—160.

[4]Anderson A B,Basilisky A,Hum D PJ.Missing Data: A Review Literature[G].Handbook of Surgery Research New York, 2002.

[5]Dempster A.P.,Larid N.M.,Rubin D.B..Maximan likelihood estimation from incomplete data via the algorithm[J].J Roy statist Soc B,1997,(39):1—38.

[6]Mark A Kramer Nonlinear Principal Component Analysis Using Auto associative Neural Networks[J].AIChE J, 1991,37(2):233—243.

[7]Scholz M.Kaplan F.Gug CL.Kopka J.Selbig J Non-linear PCA:a missing date approach.Bioinformatics，2005，21(20):3 887—3 895.

[8]李杰.主成分分析模型在天然气用量预测中的应用研究[J].阴山学报,2016，(4).

责任编辑：卢宏业

10.3969/j.issn.1674-6341.2016.05.013

2016-08-17

韩榕生(1970—)，男，理学博士，副教授，硕士研究生导师。研究方向：生物物理、计算物理、理论凝聚态物理。

TP39

A

1674-6341(2016)05-0030-03