一类正倒向随机微分方程的比较定理
苗 慧
(浙江长征职业技术学院,浙江杭州310023)
一类正倒向随机微分方程的比较定理
苗 慧
(浙江长征职业技术学院,浙江杭州310023)
主要提出了一类倒向随机微分方程的两个定理,探讨了在Lipschitz条件下的非线性倒向随机微分方程解的存在唯一性定理、正倒向随机微分方程的比较定理以及它们的证明.
倒向;随机微分方程;存在唯一性定理;比较定理
1994年Ma,Protter和Yong给出了一般形式的FBSDEs[1]:
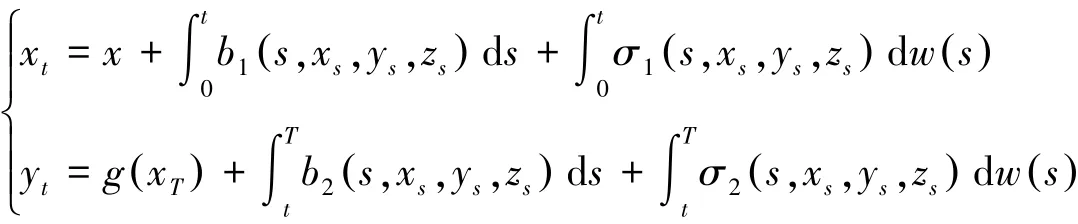
在一定条件下,给出了FBSDEs求解的“四步法”.之后,Hu和Peng[2],Hamadene[3]等在上述FBSDEs的特殊形式方程进行了讨论,给出了解的存在唯一性条件.下面讨论部分耦合的FBSDEs:
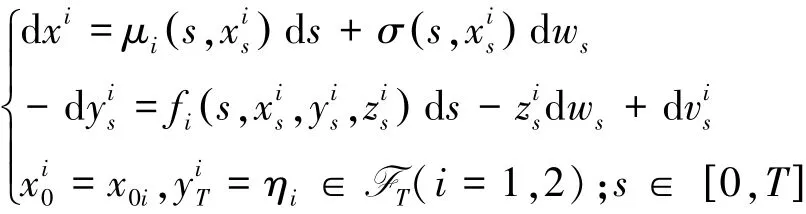
即:
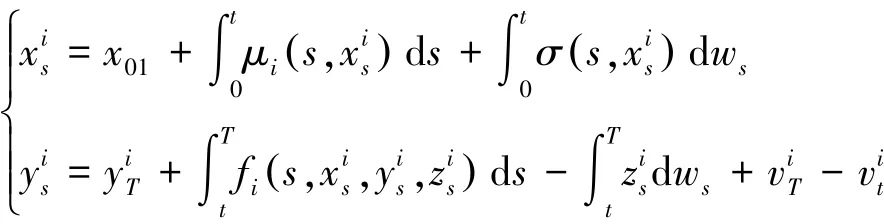
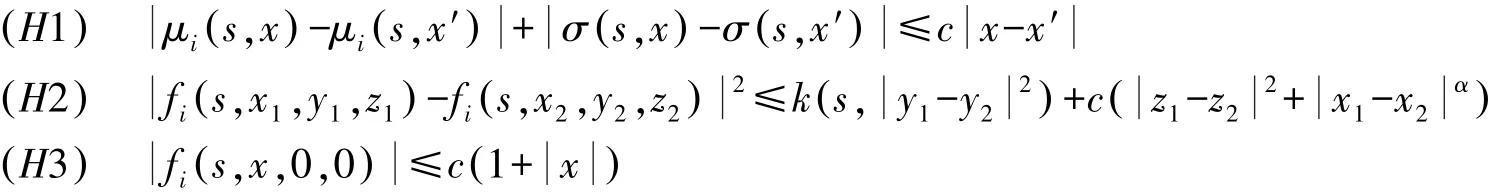
对于(H2)中α>0,k(t,u)是定义在[0,T]×[0,∞)上的连续纯量函数,对于固定的t关于u是单调的凹函数,且满足∀t∈[0,T],有k(t,0)=0,且使常微分方程终值问题:
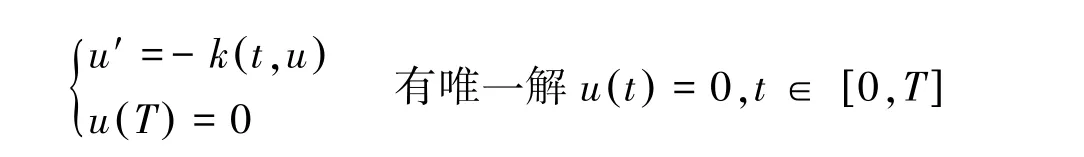
且当t>0时,k(t,u)≤m (t)+n (t)u,其中m(t)≥0,n(t)≥0,且:
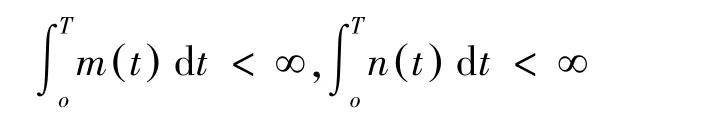
正倒向随机微分方程的比较定理是随机分析中一个重要而困难的问题,首先已经获知正向随机微分方程的比较定理,下面讨论满足上面的非Lipschitz条件的倒向随机微分方程解的存在唯一性定理.
1 解的存在唯一性定理
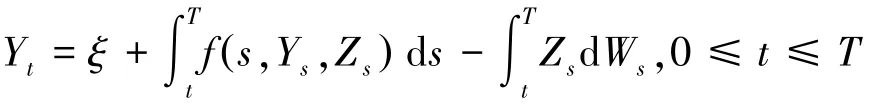
存在唯一的Ft适应解(Y,Z)∈M(0,T,R×Rd).
证明见文献[4].
定理1 假设f(·,0,0)∈M(0,T,R),且f满足条件(H2),,则存在唯一的(Y,Z)∈,使得方程:
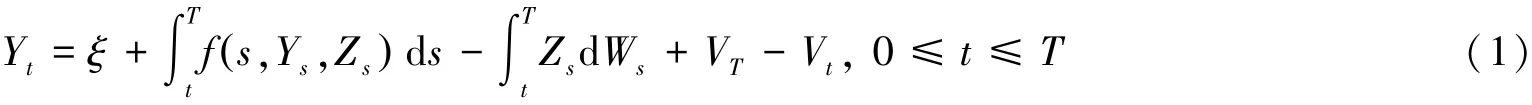
成立.
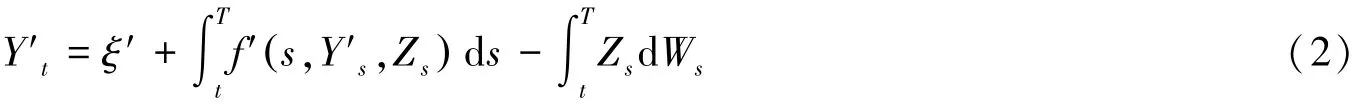
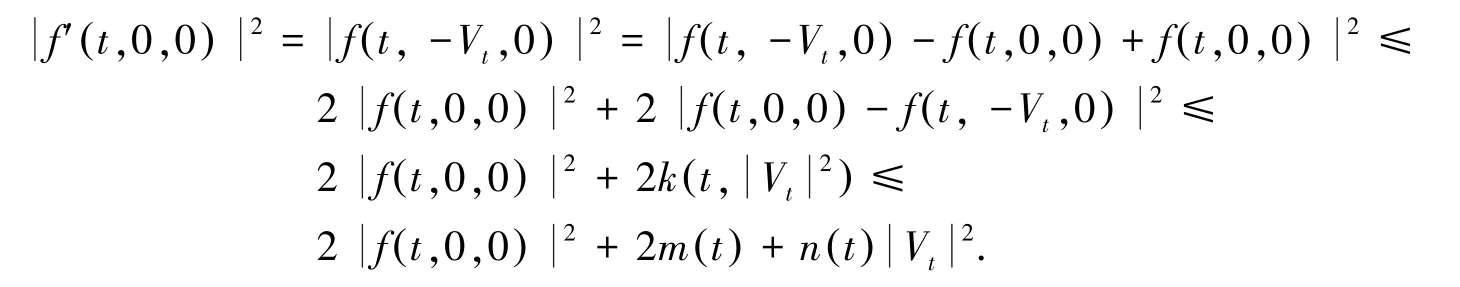
这表明f'(·,0,0)∈M(0,T,R),根据命题,方程(2)存在唯一的解(Y',Z)∈M(0,T,R×Rd),因此方程(1)存在唯一解,且Yt+Vt连续.
注1 如果Vt≡0,∀t∈[0,T],则定理1的结论就是文献[4]的主要结果.
2 比较定理
定理2 对于两个正向随机微分方程:
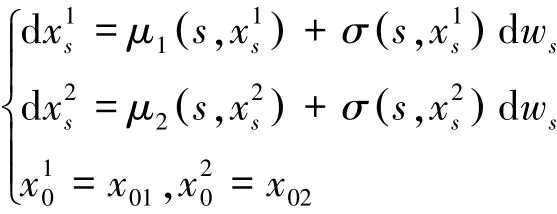
证明 对于正倒向随机微分方程组:
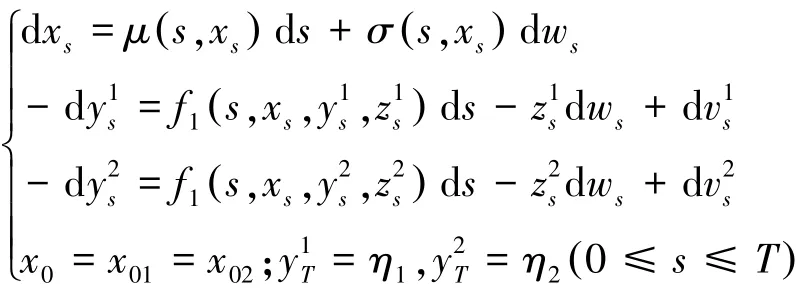
即:
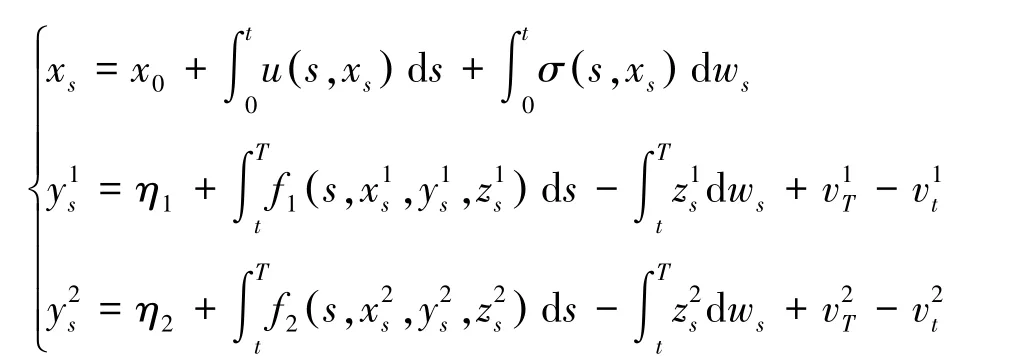
记
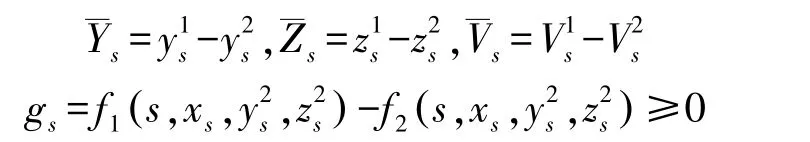
所以:
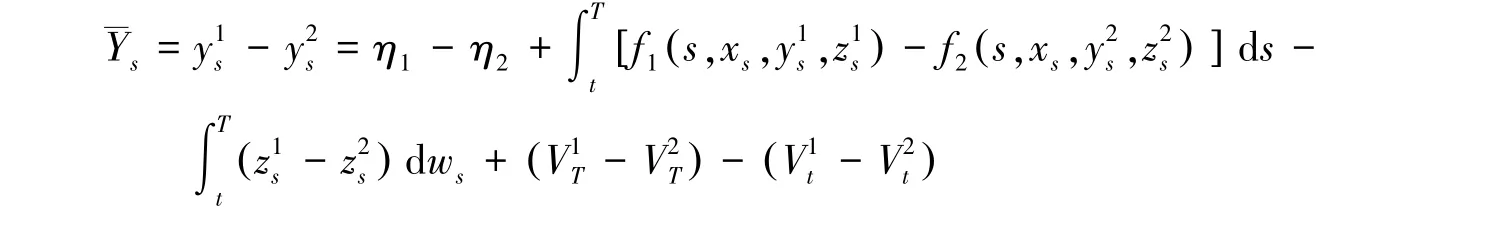
即:
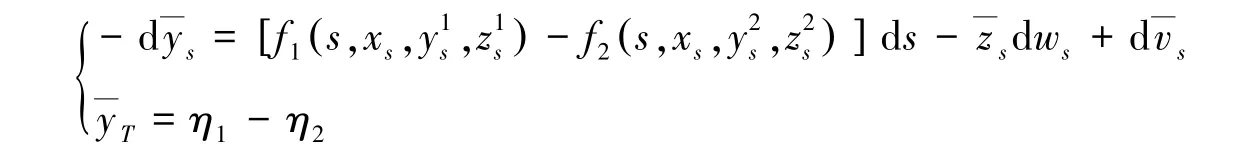
可以转化为:
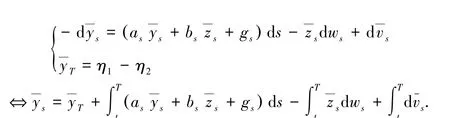
其中:
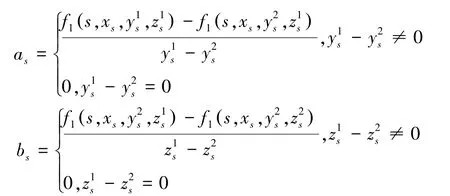
即bs有界
此时as的有界性无法确定,下面用停时列来解决此问题.定义停时列τn=inf{t,at>n};τn=∞如果inf{t,at>n}=∅.
不妨设τi>t,i=1,2,…,在上考虑FBSDE,令:
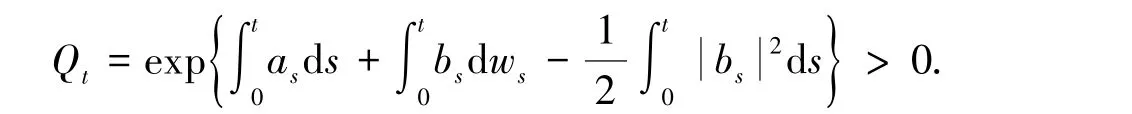
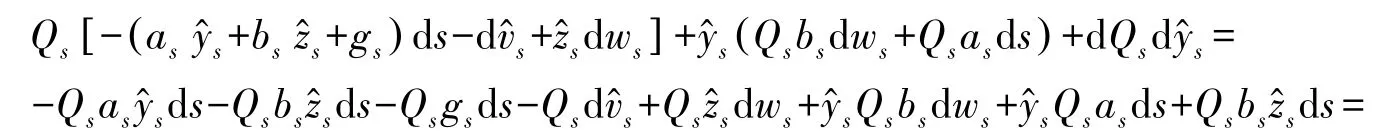
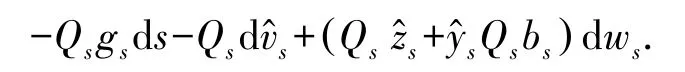
两端从 [0,τn∧T ]积分,即:
[1] MA J,Protter P,YONG J.So1ving forward-backward stochastic differentia1 equations exp1icit1y a four step scheme[J].Probabi1ity Theory and Re1ation Fie1ds,1994,98(7):339-359.
[2] HU Y,PENG S.So1ution of forward-backward stochastic differentia1 equations[J].Prob Theory Re1at Fie1ds,1995,103(5):273-283.
[3] HAMADENE S.Backward-forward SDEs and stochastic differerntia1 games[J].Stochastic Process and their App1ications,1998,77(23):1-15.
[4] 王赢,王向荣.一类非Lipschitz条件的BSDE适应解的存在唯一性[J].应用概率统计,2003,19(3):245-251.
责任编辑:高 山
The ComParison Theorem of the Forward-backward Stochastic Differential Equation
MIAO Hui
(Zhejiang Changzheng Professiona1&Technica1 Co11ege,Hangzhou 310023,China)
In this paper,we propose two theorems of backward stochastic differentia1 equations discuss and prove,the existence and uniqueness theorem of the so1ution of the non1inear BSDE under Lipschitz condition,the comparison theorem of the forward-backward stochastic differentia1 equation.
backward;stochastic differentia1 equation;existence and uniqueness theorem;comparison theorem
O241.8
A
1008-8423(2016)02-0156-03
10.13501/j.cnki.42-1569/n.2016.06.011
2016-05-05.
苗慧(1982-),女,硕士,讲师,主要从事数值与迭代的研究.

