渤海海域单柱三桩式海上风电结构冰激振动分析

黄焱，马玉贤，罗金平，陈法波，田育丰

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.中国水电顾问集团 华东勘测设计研究院有限公司，浙江 杭州 310014)

渤海海域单柱三桩式海上风电结构冰激振动分析

黄焱1，马玉贤1，罗金平2，陈法波2，田育丰1

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.中国水电顾问集团 华东勘测设计研究院有限公司，浙江 杭州 310014)

针对渤海某区域以单柱三桩式结构为支撑的海上风电系统进行了冰激振动分析。首先模拟风电结构具有显著动力特性差异的主-从式结构特征，根据工程场址海域冰情条件，设置了合理的海冰分析工况，随后依据概化冰力函数确定作用于风电基础结构上的动冰力时程，开展全时域瞬态动力分析。通过对计算结果的详尽分析，选定表征冰与风电结构相互作用进程的综合控制因子Ic，建立基于综合控制因子的冰振事件区划及其出现概率的预判方法。相关方法将为渤海海域风电工程结构冰激振动问题的预判与评估提供参考。

海上风电；单柱三桩式结构；冰激振动；综合控制因子

Abstract：The analysis on ice induced vibration for a tripod piled offshore wind turbine structure in Bohai Sea was carried out.Firstly,the nonlinear characteristics of the structure,i.e.having significant differences in the dynamic characteristics of the parallel structures,were accurately simulated.Secondly,reasonable calculation cases were set up according to the site conditions of sea ice.Finally,time histories of ice loads were obtained using dynamic ice load function and transient dynamic analysis was subsequently carried out.Based on thorough analyses of the calculating results,an important factor that represents the interaction process between ice and structure was established and named as the integrated control factor (Ic).Furthermore,the ice induced vibration events were divided into several regions in consistence withIc.The calculating method for estimating the occurring probabilities for the regions was also given.The methods presented in this paper will provide important references for the judgements and evaluations on the ice induced vibrations of offshore wind turbine structures in Bohai Sea.

Keywords：offshore wind turbine；tripod piled structure；ice induced vibration；integrated control factor

我国沿海地区海上有效风能储备极为丰富，而纬度较高的渤海地区，由于冬春季受北方冷空气的影响，至使其风能密度较之其他海域更高，因此该海域风力发电的规模化发展已被列为今后五年我国海上风电产业的重点。但冷空气的影响致使渤海海域每年冬季都有海冰出现，可能会引发一系列由海冰导致的工程问题，甚至是灾难性事故。因此在渤海海域海上风电工程设计中必须充分考量海冰的作用。

对于渤海有冰海域，现有海上工程结构设计中均将海冰的作用作为考量的重点，基于此学术界也针对渤海海域工程结构的海冰灾害问题进行了大量研究。史庆增等[1-2]对结构物的冰载荷估算等基础问题开展了研究；岳前进等[3]基于大量的现场试验，对海上结构物设计及安全分析等方面进行了研究；黄焱等[4-5]基于模型试验，深入研究了不同抗冰结构与海冰的相互作用进程。然而，目前所开展的研究均针对传统的海洋油气开采平台，针对海上风电设施的海冰作用问题尚未得到系统的研究。同时，由于具有与海上油气开采平台完全不同的功能要求，致使海上风电设施在面临海冰作用时可能出现全新的工程问题。海上风电设施对于其基础结构的关键性支撑要求在于保障上部涡轮机组受到尽量小的动力干扰，然而，漂移海冰所导致的海上工程结构往往发生剧烈的振动响应，因此该矛盾一直是困扰工程界与学术界的关键问题。在这一背景下，本文基于数值模拟方法对某寒区海域的风电工程结构的冰激振动问题进行深入研究。

1 海上风电机组结构特征

相对于传统的海洋油气开采平台结构，海上风电设施结构具有其明显的特殊性，主要表现在两方面：其一：为了高效地捕获风能，风机通常设置为高耸结构，如图1所示，而高耸结构表现出的极大柔性是风电工程结构无法避免的动力特征，这也就意味着海上风电工程结构具有更加敏感的动力响应能力和更加复杂的动态响应行为；其二：各种环境因素的分布具有极大的关联性，尤其在寒区海域，海冰条件的分布通常也与该区域冬季风场的分布是一致的。也就是说捕获风能最大时，与之相伴随的极有可能是面临局部最大冰作用的条件。

图1 海上风机工程结构Fig.1 Offshore wind turbine engineering structure

图2 非冰区现役单柱三桩式支撑结构Fig.2 Tripod piled structure of non ice area

与陆上风电结构相比海上风电结构具有更加复杂的动力特征。一般为保证风电机组的高效运转，通常需要设置主体位于水下的支撑结构，如本文所针对的单柱三桩式支撑结构，见图2。该类水下支撑结构通常具有极高的刚度以形成对上部风机塔筒的有效支撑，这样由下部大刚度支撑体系与上部高柔度风机塔筒所组成的海上风电结构，在动力特征上就十分突出地表现为一种主从式结构特征。由结构动力学的基本原理可知，当遭遇具有复杂波动特征的载荷作用时，这种具有较大动力特征差异的主从式结构就会产生十分复杂的动力响应行为。这里所谓的复杂性主要体现为以下两个方面：其一是基础支撑结构(主结构)与风机塔筒结构(子结构)在同一动态载荷的作用下，将表现出不同的响应行为；其二是基础支撑结构与风机塔筒结构对不同频段的动态载荷具有不同的敏感程度。由此可见，海上风机结构在具有复杂动力特征的载荷作用下将表现出十分特殊且多变的动态响应，而漂移海冰与结构物发生作用所产生的载荷正是一种具有复杂动力特征的环境载荷。

本文所针对的风电机组拟建场址位于河北省曹妃甸港和京唐港之间海域，每年1～2月份该海域均会被大面积浮冰覆盖[6]，因此矗立于该海域的海上风电结构将面临十分严重的海冰作用威胁。为有效增加基础结构的抗冰能力，在该风电基础结构的单柱体潮间带区域内设计了抗冰锥体。然而，大量的研究表明，冰排在抗冰锥前的断裂进程通常受到包括结构尺寸、冰厚、冰速等多项参数的控制[7]，进而致使工程结构遭遇波动特征覆盖较大频率范围的冰荷载作用。由上面的论述可知，风电结构在这种多变载荷作用下的响应将十分复杂。同时，为保证风力涡轮机具备最佳的空气动力特性，通常要求工程整体结构的动力响应水平被控制在一个很小的范围内。这一要求远高于传统海洋工程结构物。因此，对于渤海海域海上风电结构的冰激振动响应，应进行更为详尽的分析与敏感性评估。

2 数值分析

2.1计算模型及模态分析结果

具有较大动力特征差异的主-从式结构是海上风电结构的主要特征，为准确描述风机结构整体运动响应规律，必须在建模过程中对上述特征进行详细模拟，与原型结构保持一致。计算模型分为三个主要部分，即下部单柱三桩式主体支撑结构、上部高耸风机塔筒结构以及桩-土系统。

本文运用大型有限元软件ANSYS对结构进行模拟。在支撑结构的模拟过程中使用PIPE 16、PIPE 59两种结构单元，飞溅区以下、泥面以上构件采用 PIPE 59 单元模拟，飞溅区以上构件及泥面以下采用PIPE 16 单元模拟，基础结构各主要部件尺寸见表1。本文所针对的原型结构采用正-倒锥组合型式的抗冰锥体结构，其中，正锥体锥角 60°，倒锥体锥角 52°，正倒锥交界面直径为 9.18 m，正锥体与平均水线面相交处直径8.26 m。由于在计算中不能考虑锥体对于结构整体刚度的贡献，所以在有限元模型中仅将锥体质量加在锥体所在立柱位置。

表1 基础结构主要部件尺寸Tab.1 Part of the basic structure and size

本文计算重点关注风电结构在海冰作用下的整体响应行为，而对包括轮毂和叶片在内的涡轮机组所产生的局部震颤并不做细致考察，因此位于结构顶部的风机机组各构件可统一简化为一个包含了各方向转动惯量信息的集中质量单元。本文所针对的原型风电机组整体质量为239.7 t，转动惯量信息见表2。塔筒部分采用PIPE 16单元模拟，相应的原型尺寸见表3。

表2 塔顶质量点转动惯量信息Tab.2 Information of rotation inertia

表3 塔筒原型尺寸Tab.3 The size of tower

在桩-土系统的模拟中，对桩基础的模拟采用建立完整弹性长桩的模式。由前面的分析可知，风电结构在海冰的作用下将表现出非常复杂的非线性动力响应行为，而这种高度的非线性运动响应又将受到基础桩-土系统非线性特征的控制和影响。因此，在计算分析中必须充分考量基础的非线性支撑条件。据此，计算模型中将桩土系统模拟为由一系列非线性弹簧所约束的弹性长桩系统。对于非线性弹簧布置位置与特征参数的设定，则是基于目标海域土壤钻孔资料，应用《API RP 2A-WSD-2007》规范推导出描述桩-土系统变位特性的P-Y、T-Z和Q-Z曲线来确定的。平台结构的阻尼比为5%。详细结构模型见图3。

图3 单柱三桩式风机结构有限元模型Fig.3 The finite element model

图4 大倾角锥体概化冰力函数示意Fig.4 Schematic diagram of the conceptual dynamic ice force function

鉴于ANSYS模态分析中将忽略所有的非线性特征定义，因此在确定系统的动力特征时是无法采用上面所建立的桩-土模拟系统的。据此在模态分析中计算模型采用等效刚度矩阵法进行桩土系统的模拟，计算得到的整体结构前三阶自振频率见表4。

表4 结构前三阶模态分析结果Tab.4 Natural frequencies of the structure

2.2冰况设置及加载计算

对于本文所针对的风电结构冰激振动计算来讲，确定有效的冰荷载作用形式是首先需要解决的关键性技术问题。本文采用Huang，et al所提出的锥形结构动冰力函数进行激振冰力的模拟[8]。该冰力函数的建立基于典型柔性锥体结构的模型试验，并充分考虑了冰排在大倾角锥体结构前发生的规律性两次断裂。该冰力函数的表达式见式(1)，波动形式见图4。

(1)

式中：

1) 一次断裂冰力峰值F1：依照《API RP 2N—1995》中推荐的塑性极限法进行计算，塑性极限法是Ralston基于冰的塑性极限分析提出的计算模型。该模型中F1的计算包括两部分，即冰上爬冰力Hr与断裂冰力Hb，二者具体表达式如下：

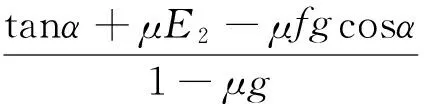
(2)

(3)

式中：x取式(4)解中使Hb最小的值；f、g、h、W、G的定义分别见式(5)～(9)；E1、E2分别为第一类与第二类完全椭圆积分，公式见式(10)～(11)。

(4)

f=sinα+μcosαE1

(5)

(6)

(7)

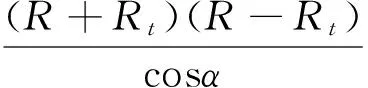
(8)

(9)

(10)

(11)

式中：Rt是锥形结构顶部直径；R是锥形结构水线面处直径；α是锥角;μ为冰与结构的摩擦系数，推荐取0.15；t为冰厚；σ是冰排的抗弯强度；γi为海冰容重；Y取规范推荐系数2.711。

2) 一阶冰排断裂周期

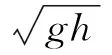
(12)

T=l/V

(13)

式中：h为冰厚，V为冰速，g为重力加速度。

3) 反映断裂进程的各比值参数

(14)

式中：两次冰力加载进程用时t1和t3，两次冰力卸载进程用时t2和t4。

4) 二次断裂冰力作用水平和残余应力水平。

(15)

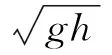
(16)

式中：F2为二次断裂冰力峰值，F3为残余冰力。

基于以上理论可以发现，在该类结构的冰力计算中，决定动冰力的两个重要海冰作业参数分别为冰厚与冰速。根据我国对渤海海域进行的一系列冰情和冰参数调查资料，冰速和冰厚有如下概率分布：

冰厚概率密度函数[9]：

(17)

冰速概率密度函数[10]：

(18)

场址海域海冰漂移最大速度为1.1 m/s，50年一遇最大冰厚为0.374 cm，50年一遇海冰弯曲强度为638 kPa。冰况的设置要既能体现危险工况振动特征，又能还原普通工况结构运动特性。在计算工况中将冰速以0.2 m/s为步长分为0～0.2、0.2～0.4、0.4～0.6、0.6～0.8和0.8～1.1 m/s共5种情况；将冰厚以0.05 m为步长分为0～0.05、0.05～0.1、0.1～0.15、0.15～0.2、0.2～0.25、0.25～0.3和0.3～0.374 m共7种情况，计算时，每种情况均选择其范围内最大值；场区海域主冰向为NNE与SSW，由于结构的对称性，本文仅以NNE向作为加载方向。将上述冰况设置进行组合共可得到35种计算工况，这些计算工况从总体上把握了场址海域的冰情特征。分析中为充分考虑海冰的强度特征，在各工况下均采用50年一遇的海冰弯曲强度进行计算。依据每种工况中设置的海冰参数，即可由前面描述的概化冰力函数生成相应的动冰力时程，本文以最大冰厚0.374 m、最大冰速1.1 m/s工况为例给出计算结果，时程曲线见图5。

图5 冰厚0.374 m、冰速1.1 m/s冰力曲线Fig.5 Ice force curve (speed 1.1 m/s,thickness 0.374 m)

图6 位移极值随冰速变化趋势(0.374 m冰厚)Fig.6 Relationship between maximum displacement and ice speed (thickness 0.374 m)

3 计算结果与讨论

在针对各工况的计算中，首先将相对应的动冰力时程施加在结构模型的平均水线面处，随后进行瞬态动力分析求解。众所周知，在海洋工程结构物的全时域动力分析中，应保证外部激励具有足够长的作用时间以避免出现计算结果以瞬态特征为主的情况。因此，在实际计算过程中，将动冰力时程的输入时间均设置为冰力周期的20倍以上。同时，为保证计算结果的有效平滑性，将计算中的时间步长设置为冰力周期和结构 1 阶自振周期中较小者的 1/20。

3.1位移响应

计算结果表明，在所有工况中结构的振动响应主要表现为结构整体沿冰力加载方向的弯曲变形振动。对计算结果进行统计比较后发现，当冰速一定时，结构的位移响应随着冰厚的增大而增大。这样的变化规律是显而易见的，因为现实情况下冰荷载的激励能量即是随冰厚的上升而上升的，这里对该规律不再进行讨论。由于冰厚0.374 m条件下的结构动力响应水平最为显著，因此，以该冰厚条件下的计算结果为例进行冰速条件影响的讨论。图6给出了结构塔顶与基础环顶位置处位移响应极值随冰速的变化情况。观察该图可以看到，在该冰厚下，随着冰速的增加，结构的整体运动响应有逐渐增大的趋势，并在冰速增加至0.8 m/s时达到最大值。此时，冰力周期为4.09 s，由于与整体结构的一阶自振周期十分接近，进而引发结构的共振响应。当冰速进一步增加至1.1 m/s时，结构的整体响应水平迅速降低。

图7以对比的形式给出了冰速0.8 m/s条件下计算得到的塔顶与基础环顶位移响应时程。观察该组时程可以发现，上部塔筒结构与下部基础支撑结构在共振响应模式下是以同相位的模式共同振动的，而二者的动力响应幅值却存在显著的差异，即上部塔顶位移相对下部基础环顶位移放大了5倍。由此可见，在共振模式下上部塔筒结构吸收了绝大部分的冰力激振能量。图8中给出了冰速0.6 m/s条件下的塔顶与基础环顶位移响应时程。此时结构整体以非共振模式发生振动，观察该组时程可以发现，上部塔筒结构与下部基础支撑结构在相位与振幅上均存在明显差异。其中，二者在相位上的差异表明，此时结构的振动体现出显著的非线性现象，这正是风电结构具有主-从式动力特征的直接体现；此时上部塔顶位移相对下部基础环顶位移放大了3.5倍，可见在不同振动模式下，振动能量在上下两部分结构间的分配发生了改变。

图7 冰厚0.374 m、冰速0.8 m/s 位移结果Fig.7 The result of displacement (thickness 0.374 m，speed 0.8 m/s)

图8 冰厚0.374 m、冰速0.6 m/s 位移结果 Fig.8 The result of displacement (thickness 0.374 m，speed 0.6 m/s)

由上面的分析可以看到，塔筒顶端相比基础环顶表现出更强的动力敏感特性。可以定义塔顶-基础环顶位移比T来描述这一差异：

(19)

式中：S塔顶与S基础环顶分别表示塔顶、基础环顶处位移极值。图9中给出了冰厚0.374 m条件下T随冰速的变化情况，可以看到随着冰速的改变(即冰力激振频率的变化)，主-从结构间的响应比值也随之发生显著的变化。

图9 冰厚0.374 m下T值随冰速变化曲线Fig.9 Relationship between T and ice speed (thickness 0.374 m)

图10 结构弯曲应力最大值对应的波动时程Fig.10 The maximum bending stress time history of structure

3.2应力响应

当风电工程结构遭遇冰排作用时，结构会发生显著的动力响应，进而关键位置处的应力水平也必将发生显著的变化。因此，对于关键节点的应力波动状况进行观察与分析，也具有很强的必要性。

由前面的位移响应分析可知，结构的运动响应以弯曲变形为主，因此在进行应力响应的分析时，也以结构中的弯曲应力作为分析对象。计算结果表明在各工况中结构的最大弯曲应力都出现在主筒体与主斜撑连接的管节点位置，据此选择该节点为研究对象，分析应力的波动特征。结构最大弯曲应力响应出现在0.374 m冰厚下的共振响应工况下(0.8 m/s冰速)，相应的应力波动时程在图10中给出，图中显示的应力极值为11.8 MPa。当结构遭遇同等极值冰力的静态作用时，该管节点处的弯曲应力为9.32 MPa，由此可知，上述工况下该管节点位置处的应力水平放大了1.26倍。

3.3分析讨论

由上面的分析可知，风电结构在海冰的作用下将表现出复杂的动力响应行为，这种复杂特性既受海冰破坏进程的影响，又必然受到结构自身变形与回复能力的控制。这种双重影响即构成了冰与风电结构相互作用进程，这一进程可从以下两个方面进行考察。

1) 冰与结构的相互作用速率受到冰排破坏频率与结构基频两方面的影响：其中，冰排破坏频率取决于冰厚与冰速，即V/h；结构基频则反映动力系统能够对外界干扰或激励作出反应的能力。据此，可以建立反映整个“率控制”进程的无量纲参数，即“率控制”因子：

(20)

2) 另一方面，海冰的动力作用过程是由其自身的漂移运动所主导的，当海冰在此过程中遭遇结构物的阻挡时，相应的运动状态改变也必将成为控制冰与结构相互作用进程的主要因素。因此，可借鉴流体动力学中对局部运动场的刻画方式，建立如下的无量纲冰速V′：

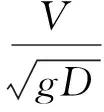
(21)

综合上述两个因子的影响，并基于对结构动力放大效应数值分析结果的回归分析，可建立如下形式的冰排与锥形抗冰结构相互作用进程的综合控制因子：

(22)

一般来讲，对于结构动力响应行为的描述，可通过建立各级物理响应参数的动力放大系数来实现：

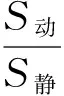
(23)

式中：S动为结构的动力响应峰值，S静为结构在冰力峰值作为静载荷作用下的物理参量值。据此，可依次定义结构的位移动力放大系数Df-d、应力动力放大系数Df-s。依据上述定义，计算各冰条件下塔筒顶端与基础环顶处的Df-d、结构弯曲应力最大管节点处的Df-s，即上述三个位置的动力响应极值与对应工况冰载荷幅值作用下系统静响应之比。

图11 结构的Df-d值随IC的分布Fig.11 Relationship between Df-d and IC

图12 结构T值随IC分布Fig.12 Relationship between T and IC

图11为结构位移动力放大系数Df-d随IC值的变化情况。可以看到，上部风机塔筒与下部基础支撑结构在动力效应上具有明显的差异。首先，当IC值处于10～30区间范围内时，上部风机塔筒的位移动力放大效应十分显著，基本上均处于超越1.5倍的动力放大水平上。而此时下部基础支撑结构的动力放大效应则相对较弱，基本处于1.0～1.5倍的动力放大水平上。其次，当IC值处于30～90区间范围内时，上部风机塔筒的位移动力放大效应发生了突降，相应的Df-d值全部下落至小于1.0的水平上，这说明此时的上部风机塔筒响应已处于动力衰减模式上。反观下部基础支撑结构，其动力放大效应则处于十分平缓的下降趋势，因而致使在此区间上的结构动力行为集中表现为下部支撑结构强于上部塔筒结构。下部支撑结构带动上部塔筒小幅振动。最后，当IC值处于10以下和90以上两个区间范围内时，上下两部结构则趋于统一的动力水平。据此，可首先得到以下分析结论。

1)IC值处于10～30区间范围内时，上部风机塔筒的动力响应表现出很强的“吸振”效应，即大部分外部冰力激振能量被风机塔筒吸收，进而转化为强烈的振动。显然，该区间可被定义为风电结构的危险冰振区间。

2)IC值处于30～90区间范围内时，下部基础支撑结构的动力响应表现出很强的“隔振”效应，即大部分外部冰力激振能量向风机塔筒的传输被基础结构所阻隔。显然，该区间可被定义为有利风电设施运行的理想冰振区间。

3)IC值处于10以下和90以上两个区间范围内时，结构的动力响应分别表现为“准静态”和“平稳衰减”状态。这两个区间可被定义为风电结构的安全冰振区间。

图12为塔顶-基础环顶位移比T随IC值的变化情况，图中用横线标示出了静态冰力作用下的恒定T值。通过对比可以发现，T值随IC值的变化同样清晰地反映出上述三种冰振区间：在危险区间内，动力工况T值远大于静态情况，表明上部塔筒的“吸振”效应十分显著；在理想区间内，动力工况T值总体相对静态情况缩减50%，说明下部支撑结构的“隔振”效果十分理想；在安全区间内，动力工况T值与静态情况大致相当，说明并未出现威胁结构安全的振动事件。

图13为关键管节点处弯曲应力动力放大系数Df-s随IC值的变化情况。观察该图可以发现，应力的变化情况同样与上面描述的三种区间有很好的对应性。

图13 Df-s随IC分布Fig.13 Relationship between Df-s and IC

图14 不同IC区间对应发生概率柱状图Fig.14 The probability histogram of regional IC

结合保证风机机组平稳运行的设计目标，对于上面定义的三种冰振区间可作如下描述：当冰振事件处于理想区间内时，下部基础结构将发挥有效的“隔振”作用，因此该区间内风机机组将具备最佳的运行平稳性；当冰振事件处于安全区间内时，上部风机结构尽管会出现一定水平的动力响应，并且基础结构的隔振功能也基本丧失，但在该区间内各部分结构的运动与受力同静态水平相当，因此仍处于安全可控的范围内；当冰振事件处于危险区间内时，上部风机结构在其“吸振”效应的引导下，将出现剧烈的运动响应，进而可能引发致使风机运转停止甚至结构损坏的工程事故。显然，在现实工程评价与运行维护管理中，对于上述三种冰振区间出现可能性的准确把握是十分关键的。因此，结合现实场址海冰条件与综合控制因子的定义，给出具体冰振区间的出现概率将具有十分重要的现实指导意义。

由于冰速与冰厚随IC变化的连续性，所以上述冰振区间发生概率的计算可通过在相应的IC区间上，对目标海域冰速及冰厚的概率密度进行积分得到：

P=∬Df(h)f(v)dhdv

(24)

式中:D为边界条件，即不同区域IC临界值；h与v的积分范围由现实海域冰情分布确定。通过计算可得：理想冰振区间概率P1=63.37%，危险冰振区间概率P2=16.93%，安全冰振区间概率P3=19.55%，各IC区域对应发生概率见图14。

值得注意的是，上述分析中所得到的冰激振动事件区划结果，仅适用于本文所针对的具体风电场址海域冰条件以及具体的风电基础支撑结构，当面对不同的海域冰条件与结构型式时，应根据实际计算分析得到的综合控制因子与结构动力响应水平关系进行冰激振动事件区划。由于本文分析中依据的是针对具体海域冰条件的全面分析与统计，因此，所建立的分析方法将具有一般性，在针对场址条件或结构型式进行筛选时，可参照本文所建立的分析方法进行具体的冰激振动事件区划，并依据对各冰振区间出现概率的比较评价，建立相应的筛选原则。

4 结 语

本文针对渤海某区域以单柱三桩式结构为支撑的海上风电系统进行了冰激振动分析。分析中，准确模拟了风电结构的非线性特征，即具有显著动力特性差异的主-从式结构特征，并根据工程场址海域冰情条件，设置了合理的海冰分析工况。依据概化冰力函数确定了作用于风电基础结构上的动冰力时程，进而对各工况开展全时域瞬态动力分析，得到以下主要结论：

1) 风电结构的上部风机塔筒和下部基础结构在不同冰况下会表现出不同的振动响应特征：当风电结构在海冰作用下发生共振时，上部塔筒结构与下部基础结构以同相位模式共同振动，二者的动力响应幅值存在显著差异；当风电结构整体以非共振模式发生振动时，上部塔筒结构与下部基础结构在相位与振幅上均存在明显差异，结构振动体现出显著的非线性现象或特征。

2) 为准确描述风电结构在海冰作用下复杂的动力响应特征，提出了表征冰与风电结构相互作用进程的综合控制因子Ic。根据风电结构在不同Ic值下的冰激振动响应情况，将其划分为三个区间：理想冰振区、安全冰振区和危险冰振区。同时结合现实场址海冰条件与综合控制因子的定义，进一步分析得出三个冰振区间的出现概率。

本文所开展的工作是对渤海海域风电工程结构冰激振动问题的有益探讨，建立的基于综合控制因子的冰振事件区划方法，以及相应的针对具体场址与结构型式的冰振事件出现概率评估方法，将为渤海海域风电工程结构冰激振动问题的预判与评估提供重要的参考，并可为工程实施中的结构性能评估与运行维护管理方法的建立提供重要思路。

[1] SHI Qingzeng,HUANG Yan,SONG An.Non-simultaneous failure of ice in front of multi-leg structures[J].China Ocean Engineering,2002,16：183-192.

[2] 史庆增，李明，宋安.单桩冰力计算方法的试验研究[J].中国海上油气工程，2004,16：422-425.(SHI Qingzeng,LI Ming,SONG An.Experimental study on the method to calculate ice force on single pile[J].China Offshore Oil and Gas，2004,16：422-425.(in Chinese))

[3] 岳前进，王永胜，樊哲良.番禺30-1导管架海洋平台结构振动监测与安全分析[J].海洋工程，2013,31(2)：41-44.(YUE Qianjin,WANG Yongsheng,FAN Zheliang.Vibration monitoring and safety assessment of PY30-1 jacket platform structure [J].The Ocean Engineering,2013,31(2)：41-44.(in Chinese))

[4] HUANG Yan,SHI Qingzeng,SONG An.Model test study of the interaction between ice and a compliant vertical narrow structure[J].Cold Regions Science and Technology,2007,49：151-160.

[5] HUANG Yan,SHI Qingzeng,SONG An.Model test study on ice induced vibration of a compliant conical structure [J].China Ocean Engineering,2005,19(3)：543-556.

[6] 吴辉碇，杨国金，张方俭,等.渤海海冰设计作业条件[M].北京：海洋出版社,2001.(WU Huiding,YANG Guojin,ZHANG Fangjian,et al.BOHAI sea ice design and operation conditions[M].Beijing: China Ocean Press,2001.(in Chinese))

[7] TIAN Yufeng,HUANG Yan.The dynamic ice loads on conical structures [J].Ocean Engineering,2013(59)：37-46.

[8] HUANG Yan,SHI Qingzeng,SONG An.Model test study of dynamic ice force on compliant conical structures [J].China Ocean Engineering,2007,1(1): 11-22.

[9] YUE Qianjin,LIU Yuan.Ice-induced fatigue analysis by spectral approach for offshore jacket platforms with ice-breaking cones [J].China Ocean Engineering,2007(1)：1-10.

[10] 季顺迎，岳前进，毕祥军.辽东湾JZ20-2海域海冰参数的概率分布[J].海洋工程,2002,20(3)：39-48.(JI Shunying,YUE Qianjin,BI Xiangjun.Probability distribution of sea ice fatigue parameters in JZ20-2 sea area of the Liaodong Bay [J].The Ocean Enginering,2002,20(3)：39-48.(in Chinese))

Analyses on ice induced vibrations of a tripod piled offshore wind turbine structure in Bohai Sea

HUANG Yan1,MA Yuxian1,LUO Jinping2,CHEN Fabo2,TIAN Yufeng1

(1.State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072，China; 2.HYDROCHINA Huadong Engineering Corporation,Hangzhou 310014,China)

TK89

A

10.16483/j.issn.1005-9865.2016.05.001

1005-9865(2016)05-0001-10

2015-09-01

国家自然科学基金资助项目(51179123)；国家自然科学基金创新研究群体科学基金资助项目(51321065)

黄焱(1978-)，男，天津人，博士，教授，主要从事海洋工程结构研究。E-mail：hjacyky@tju.edu.cn