基于模型优化的Android平台虚拟加工系统设计
褚人宇 施 群 游玉霖
(上海大学机电工程与自动化学院,上海 200072)
基于模型优化的Android平台虚拟加工系统设计
褚人宇施群游玉霖
(上海大学机电工程与自动化学院,上海200072)
针对移动平台上实现虚拟加工仿真需要解决仿真模型数据量过大及仿真效果差的问题,提出了基于STL简化的三角模型及优化Z-Map算法。该算法适用于五轴数控加工,提高了仿真程序运行效率;同时给出了Z-Map网格优化方法,保证了系统在移动平台上的运行效果。在Android平台上搭建了虚拟加工仿真系统。试验结果验证了该算法在Android平台上与虚拟加工结合的可行性以及良好的仿真效果。
移动平台STL模型Android平台Z-Map算法计算机仿真虚拟制造虚拟加工五轴加工
0 引言
虚拟制造是在计算机上执行产品设计及制造的全过程[1]。虚拟模型可以在产品制造前对产品的性能和可制造性等问题进行预测及分析[2]。随着虚拟制造概念的提出[3],虚拟加工仿真技术[4]也得到了很大的发展。而随着智能制造时代的到来,各种移动设备在人们日常办公中发挥的作用也越来越大。在机械制造领域,很少看到计算机仿真技术在这些移动平台上的应用。Android系统在移动平台终端的市场占有率超过70%。本文提出并开发了基于Android操作系统的虚拟加工仿真系统。
1 仿真系统模型构建存在的问题
Android操作系统的计算能力以及图形显示能力较弱,基于Android平台的虚拟加工系统设计需要解决如下问题。
①由于机床三维模型的构造较为复杂,模型数据文件较大,在移动平台中直接读取、显示,占用的内存较大。而且在仿真过程中,需要实时刷新机床数据,数据量过大会明显影响程序运行的效果,以及切削加工时机床实时显示的连续性。在虚拟仿真系统中,机床模型采用光圈化立体造型(sterelitho graphy,STL)数据模型,采用三角片精简技术对模型数据进行处理,可以减少数据量。江本赤等[5]分析了STL模型中一些狭长的钝角三角形对模型精度的影响,并对这类三角形进行过滤。这种方法对于三角片网格比较均匀的STL模型简化效率较低。闫涛等[6]通过计算三角片权重并排序,删除了权重较小的三角片,并对剩余三角片进行重构。Schroeder[7]提出了顶点删除法的基本思想,其主要思想是判断顶点对模型的重要程度,对不重要的顶点进行删除。本文在顶点删除法的基础上,提出了STL模型优化算法。
②仿真加工的效率成为研究过程中选择仿真模型构造方法主要考虑的因素。实体构造几何法[8]最早是由Voelcker和Hunt提出的。该方法表示简洁,但是需要进行大量的布尔运算,存在计算量过大的问题。为了解决实体构造几何法计算量过大的问题,Van Hook[9]提出了Z-buffer结构,具体是将刀具按屏幕像素离散成Z-buffer结构,切削则可以简化成一维运算,大大提高了运算效率。Hsu PL[10]和Choi KB[11]将Z-buffer结构拓展,提出了Z-Map的思想,并对该方法的应用进行了介绍,证明Z-Map方法可以避免布尔运算,大大提高了仿真效率。王鹏远[12]将离散的工件模型沿着Z方向投影,进而离散成Z方向的线段。起点为投影底面的网格点,终点为模型顶面上的点,并将其应用于三轴仿真加工系统,获得了不错的仿真效果。郝大功[13]等提出了基于Z方向误差的Z-Map 模型简化算法,对Z-Map模型的网格进行了精简,提高了仿真效率,但是仿真效果并不理想。
以上文献中的Z-Map只是应用于三轴加工,并没有向五轴拓展。五轴加工的多是自由曲面,而自由曲面加工仿真的效果与网格划分的方式息息相关。若网格划分比较密集,则数据量和运算量都较大,仿真效率低。若网格划分比较稀疏,则采用Z-Map方法获取的加工表面较为粗糙,仿真显示效果差。加工仿真过程中,为了解决这一矛盾,本文提出了一种五轴自适应Z-Map模型。
2 基于STL模型优化算法
先对STL模型进行分界区处理,再对分割完成后的区块进行精简,得到精简后的STL数据。为了便于算法的描述,我们先对STL模型进行如下集合定义:STL模型是点、线、面的集合,由一个顶点出发,建立三角片各个基本元素的直接联系。三角片分区块示意图如图1所示。

图1 三角片分区块示意图
三角片模型由一个顶点Pi出发,建立其与线Lij和面Fijk的联系。
三角片精简具体算法流程如下。
①因为模型边界的改变会直接影响简化后模型的形状特征,故先对STL模型进行边界提取,判断三角片各个边是否存在共边的情况。设公共边的端点编号分别为i、 j,判断是否存在包含公共边的不同三角片。若满足条件,则该边为公共边;若不存在,则该边为模型边界,予以保留。
②判断STL模型分区块是否平坦,若平坦,则标记对应的三角片数据;若不平坦,则保留该区域原有三角片数据。以一个三角片ΔPiPjPk为中心,与中心三角片有共同顶点的三角片共同构成一个分区,作为一块判断区域。
判断每个区块是否平坦,本文提出了一种以相邻三角片法向量加权方差值作为判断区域平坦的依据。不仅相邻三角片法向量夹角对平面的平坦度有影响,三角片的大小也对分区块的平坦度有较大的影响,这里引入加权方差作为判断分区块平坦度的依据。
以相邻三角片面积A1与中心三角片面积A0的比值作为权值w:
(1)
定义中心三角片与相邻三角片之间的夹角为θ,中心三角片的法向量为n0,相邻三角片的法向量为n1,则可根据以下公式计算夹角θ:
(2)
加权方差值D(wθ)为:
D(wθ)=E(wθ)2-E2(wθ)
(3)
式中:E(wθ)为分区块中法向量的加权平均值。
方差值本身就能够反映随机变量波动程度,增加加权值后更能准确描述三角片区域的曲率波动情况。根据分区块三角片的加权均方差是否小于给定阈值σ,判断分区块平坦情况。
③删除平坦分区块中心三角形中重要程度较低的顶点,并且重新构造三角片。
平坦分区块中,相对不重要的顶点(形状较为平坦的顶点)的判断依据是顶角法向量与共用该顶点的所有三角片法向量的夹角的方差。若方差越大,则顶角越尖锐;反之,则顶角越平坦。
顶点单位法向量nPi计算公式为[14]:
(4)
式中:Fk为包含目标顶点Pi的三角片;γk为三角片在顶点Pi处的顶角;Af k为面Fk的面积;nf k为三角片的法向量;m为共顶点三角片的个数。
(5)
式中:αk为相邻三角片与顶点单位法向量的夹角;nPi为顶点单位法向量;nk为顶点邻接三角片法向量。
方差值D(α)为:
D(α)=E(α)2-E2(α)
(6)
式中:E(α)为顶点法向量与邻接三角片法向量的夹角平均值。
计算平坦分区块中心三角形顶点处的D(α)值。该值最小的顶点为最不重要的顶点,可删除并重构三角片。
重构三角片的方法如下:将去除顶点后的邻接三角片按顺序编号,分别编号Pi,Pi+1,Pi+2,…,Pi+n;分别求取间隔一个点的两个顶点之间的距离,找出其中最小的,连接组成一个三角片;再对剩余的顶点重新按顺序编号,继续寻找两线距离最短的两个点,构成三角片,直至所有三角片重构完成。
3 五轴自适应Z-Map模型
3.1五轴Z-Map求交算法
Z-Map方法之前主要应用于三轴加工,结合五轴加工的特点,提出适用于五轴加工的Z-Map算法。用如下的数据结构来表示将Z-Map离散后的线段参数:
publicclassZ-MapLines{
floatstartZ;
//Z-Map线段的起点
floatendZ;
//Z-Map线段的终点
}
publicclassZ-MapLineList{
floatx;
//Z-Map点对应投影点的x坐标
floaty;
//Z-Map点对应投影点的y坐标
List
//储存每个投影点上对应的线段及其属性
intm_LineTotally;
// 单一投影点上对应的Z-Map线段的条数}
首先,建立刀具的数学模型。由于刀具在加工时绕轴线旋转,则可以用回转体描述刀具的数学模型。若刀具为平底刀,则刀具的数学模型可以表示为圆柱体。本文以C-A双摆五轴机床为例,进行公示推演。以下公式中:I、J、K分别为刀具的矢量方向的三个分量;X、Y、Z分别为刀具上的坐标点;θ为圆周的角度;r为刀具半径;n为刀具模型上切削刃的长度;C和A分别为绕Z和X轴的旋转角度;TX、TY、TZ分别为刀具的刀尖点坐标。
当I≠0、J≠0时,在空间中的任意圆的参数方程可以用式(7)~式(9)表示。由上文可知,空间内刀具模型为圆柱面模型,由圆的参数方程可以推导出刀具圆柱面的参数方程如式(11)~式(12)所示。
x=rcosθ
(7)
y=rsinθ
(8)
z=0
(9)
X=cosC×x+sinC×(cosA×y-sinA×z)+In+TX
(10)
Y=-sinC×x+cosC×(cosA×y-sinA×z)+Jn+TY
(11)
Z=sinA×y+cosA×z+Kn+TZ
(12)
将式(7)~式(9)代入式(10)和式(11),得:
X=cosC×r×cosθ+sinC×cosA×r×sinθ+In+TX
(13)
Y=-sinC×r×cosθ+cosC×cosA×r×sinθ+Jn+TY
(14)
联立式(12)~式(14),求解:
(15)
当刀具模型与Z-Map线段求交过程中,一个Z-Map模型对应的投影点在Z方向上只存在一条线段,其考虑情况如下。
情况一:当Z-Map投影点的Z向射线与刀具模型没有交点,此时刀具与被加工物体并未发生接触,因此不发生切削。
情况二:当Z-Map投影点的Z向射线与刀具相交后产生一个交点,该交点小于Z-Map线段的最高点的值,大于Z-Map线段的最低点的值,此时刀具与被加工物体发生切削。将Z-Map线段的终点值endZ0修改为两个求得的交点中较小的值。
情况三:当Z-Map投影点的Z向射线与刀具相交后,两个交点的值均在Z-Map线段的最高点的值和最低点值之间,此时刀具与被加工物体发生切削,并且在同一个Z-Map点出现了两条Z-Map线段。这时增加线段并设其端点为(endZ1,startZ1),同时对原有线段进行修改,使得endZ0=ArrayZ1、endZ1=endZ62、startZ2=ArrayZ2。
情况四:当Z-Map投影点的Z向射线与刀具相交后产生一个交点,该交点大于Z-Map线段的最低点的值,小于Z-Map线段的最高点的值,此时刀具与被加工物体发生切削,将Z-Map线段的startZ0修改为ArrayZ2。
在刀具与毛坯直线段求交的过程中,一个投影点对应的Z空间方向上有多条线段,可以具体分析每一条线段。具体分析与上文相同。
刀具与Z-Map模型相交情况如图2所示。

图2 刀具与Z-Map模型相交情况示意图
3.2Z-Map自适应网格划分
定义网格顶点的适应度为λ,表示单个网格顶点与Z-Map模型加工表面的适应程度。
(16)
式中:ΔZi为网格顶点与相邻的Z-Map网格点在Z方向上的差值。
Z-Map自适应优化流程如图3所示。
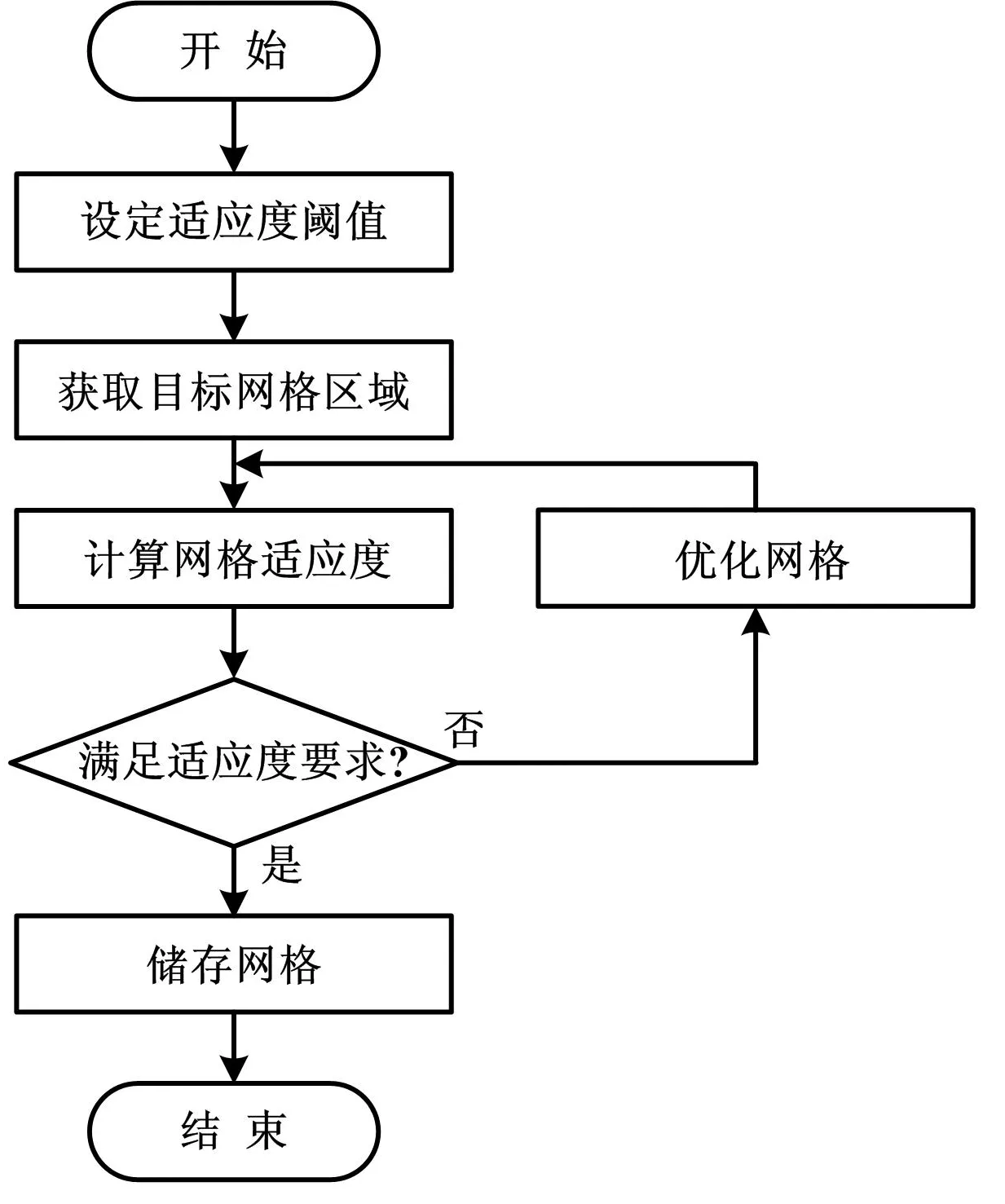
图3 自适应优化流程图
自适应优化流程具体说明如下。
①设定网格适应度阈值,该阈值体现了Z-Map模型与真实加工面的偏差程度。
②获取完成切削区域网格。五轴加工的切削过程可以被看作是多个相邻刀位的集合,前一个刀位切削到而后一个刀位没有切削到的区域就是已加工区域。刀具切削区域在网格上的投影如图4所示,阴影区域为切削过程中已完成的切削部分。
③计算Z-Map网格顶点适应度,以网格四个顶点的适应度均值作为顶点包围的网格适应度。
④对网格适应度不满足要求的阈值进行自适应优化。具体方法是选取Z向差值最大的网格边进行二等分,如此反复,直至所有网格点满足适应度要求。

图4 刀具切削区域在网格上的投影图
4 试验验证
根据上文所述,本文提出的基于Android的五轴数控加工仿真系统搭建流程如图5所示。
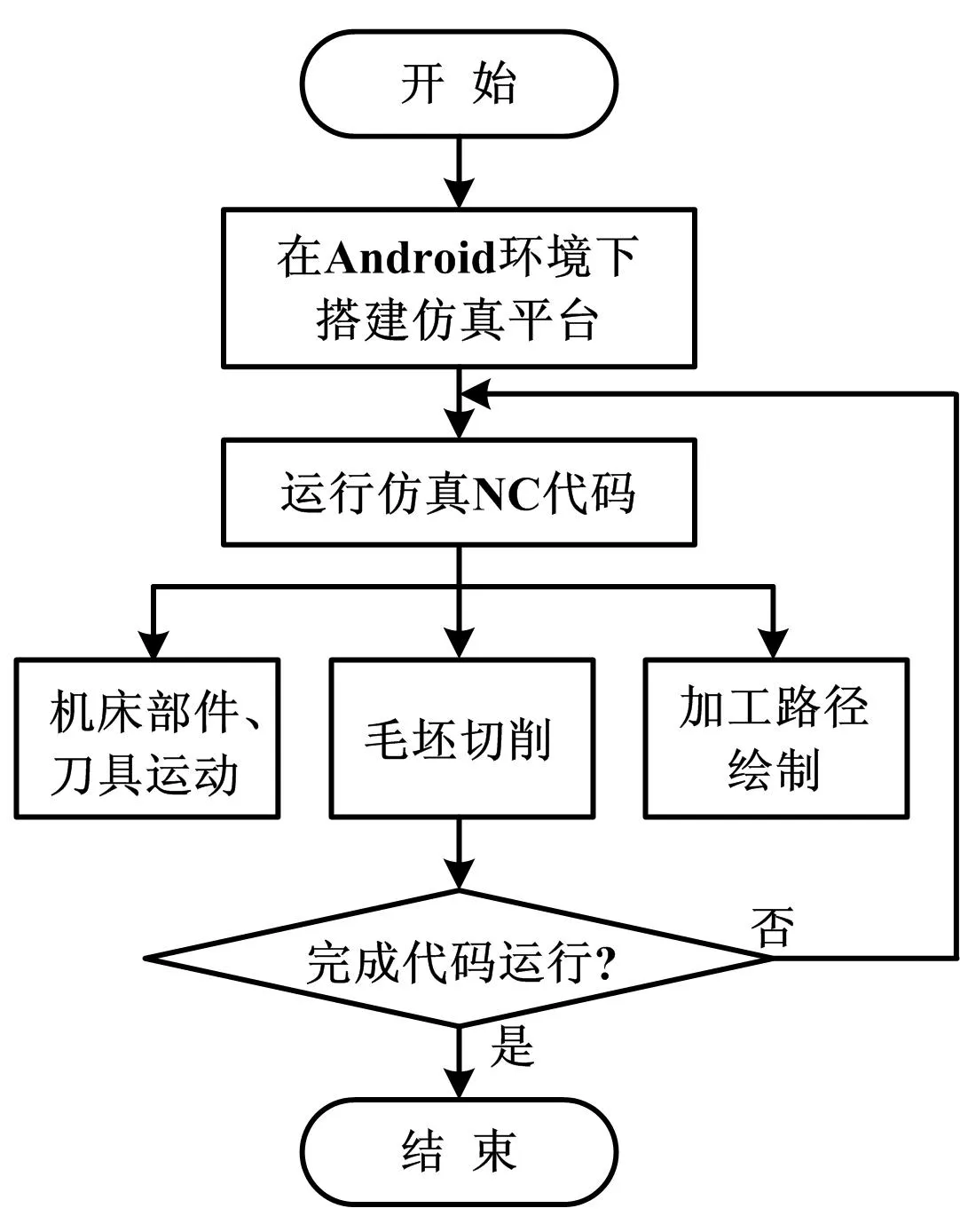
图5 虚拟仿真系统搭建流程图
虚拟仿真系统是基于OpenGLES,在Android环境下开发的。试验平台为三星N7100移动端搭载基于Android4.1的Flyme2.0深度操作系统。文件读取及操作方式采用JAVA标准I/O库。
机床模型数据量大,导入仿真平台需要一定的加载时间。经过文中STL模型优化精简方法,确定平坦度加权方差阈值为0.1,筛选次数为2次,可获得机床主轴外壳的三角片个数对比。精简前三角片个数为1 236,精简后三角片个数为423。三角片数量明显减少,而外形改变较小。
在虚拟加工平台上,三角片精简的效果以模型加载时间作为直接衡量标准。取平坦度加权方差阈值为0.1,改变精简次数,建立加载时间与精简次数关系如图6所示。经过STL精简算法导入,机床模型在虚拟加工平台重的加载时间明显减少。

图6 加载时间与精简次数关系图
虚拟加工系统仿真结果表明,采用均匀网格划分的Z-Map模型的加工表面较为粗糙,而经过本文改进的Z-Map模型的加工表面较为光滑。本文提出的自适应Z-Map方法可以有效提升仿真的效果。由试验结果可知,本文搭建的基于Android的虚拟加工仿真平台可以清晰地反映虚拟加工仿真的全过程,验证了基于Android环境开发的五轴数控加工仿真系统的可行性。
5 结束语
本文提出了一种基于模型优化的Android虚拟加工系统,将计算机仿真和虚拟加工引入到Android移动设备平台,为虚拟加工仿真技术应用的研究提供了一个新的研究方向,有利于计算机虚拟仿真加工技术向更多应用方向发展。通过分析STL文件的文件结构,并对模型进行精简,解决了STL数据量过大的问题,实现了机床在Android数控仿真系统的流畅加载与动态显示。通过优化Z-Map模型的求交方法,使其能够适用于五轴加工,并且提出了Z-Map自适应网格划分方法。在加工过程中,实时优化Z-Map网格,提高了仿真效果。最后搭建了平台上虚拟加工系统,验证了虚拟加工在Android平台上的可行性以及仿真效果。
[1]XIANGY,MALAKRC,LAUERC.Manufacturingsystemdesignwithvirtualfactorytools[J].InternationalJournalofComputerIntegratedManufacturing,2015,28 (1):25-40.
[2]DONGKL,YOUNGMINK.Studyonaprocess-centricmodelingmethodologyforvirtualmanufacturingofshipsandoffshorestructuresinshipyards[J].TheInternationalJournalofAdvancedManufacturingTechnology,2014,71(4):621-633.
[3]LEMUHG.Virtualengineeringindesignandmanufacturing[J].AdvancesinManufacturing,2014,2 (4):289-294.
[4]NOAKERPM.CAD/CAMcontrolsystemsandsoftware[J].ManufacturingEngineering,1996(3):222-240.
[5] 江本赤,郭利.STL模型简化技术研究[J].机床与液压,2009(8):231-250.
[6] 闫涛,姜晓峰.基于STL三角网格模型简化的研究[J].计算机工程与设计,2010,31(23):5060-5074.
[7]SCHROEDERW,ZARGEJA.Decimationoftrianglemeshes[J].ComputerGraphic,1992,26(2):65-70.
[8]VOELCKERHB,HUNTWA.TheroleofsolidmodelinginmachineprocessmodelingandNCverification[C]//ProceedingsofSAE1981InternationalCongressandExposition,1981.
[9]HOOKV.RealtimeshadedNCmillingdisplay[J].ACMSIGGRAPHComuterGraphics,1986,20(4):15-20.
[10]HSUPL,YANGWT.Realtime3Dsimulationof3-aixsmillingusingisometricprojection[J].ComputerAidedDesign,1993,25(4):215-224.
[11]CHOIKB,CHUNGYC,PARKJW.ApplicationandextentionofZ-Mapmodel[C]//ProceedingsoftheThirdPacificGraphicsandAppliations,1995:363-382.
[12]王鹏远.三轴数控铣削加工图形仿真技术的研究与实现[D].苏州:苏州大学,2006.
[13]郝大功,闫光荣.Z-Map模型精简技术研究[J].图学学报,2007,28(1):134-138.
[14]神会存,周来水,贺美芳.基于顶点分类的曲面三角网格模型自适应光顺研究[J].南京航空航天大学学报,2004,36(4):471-476.
Design of the Virtual Machining System Based on Model Optimization and Built on Android Platform
To solve the problems in implementing simulation of virtual machining on mobile platforms,i.e.,the excessive amount of data of model simulation,and the poor results of simulation,the STL simplified triangle model and optimizedZ-Map algorithm are proposed.The algorithms make it suitable for five-axis NC machining and improve the running efficiency of simulation program .In addition,theZ-Map mesh optimization method is given to ensure the running effect of the system on mobile platform.The virtual machining simulation system is built on Android platform; the experimental results verify the feasibility of the algorithm for combining Android platform with virtual machining,and the excellent simulation result.
Mobile platformSTL modelAndroid platformZ-Map algorithmComputer simulationVirtual manufactoryVirtual machiningFive-axis machining
褚人宇(1992—),男,现为上海大学机械制造及其自动化专业在读硕士研究生;主要从事数控技术方向的研究。
TH-39;TP391
A
10.16086/j.cnki.issn 1000-0380.201609006
修改稿收到日期:2016-02-05。

