BUCK电压反馈全桥逆变升压可调高压直流电源

徐晨剑　岳继光

(同济大学电子与信息工程学院，上海　201804)



BUCK电压反馈全桥逆变升压可调高压直流电源

徐晨剑岳继光

(同济大学电子与信息工程学院，上海201804)

针对低温等离子体发生器的相关研究试验，采用BUCK电压反馈全桥逆变升压拓扑，设计了一种可调高压直流电源。为实现电源输出对参考信号的快速跟踪，对电路各模块小信号进行建模，建立了系统环路增益传递函数，并使用Matlab分析原系统稳定性；采用双零-单极补偿器进行补偿，使用Saber对补偿后电路仿真，验证了补偿后电路的静态指标和动态特性。仿真结果表明，电源输出可渐近跟踪给定参考信号，动态特性好，实现了高压直流可调输出，可用于低温等离子体的试验研究。

低温等离子体可调高压直流电源传感器BUCK电路PWMSaber补偿Matlab

0　引言

自1988年美国环保局气体与能源工程试验室开展等离子体降解挥发性有机物和有毒气体的研究以来，低温等离子体研究在全球范围内迅速发展[1]。研究包括工业废水、废气处理，环境净化，食品灭菌等领域，并取得较好的试验效果。虽然低温等离子体研究方法的效率很高，但因等离子体高昂的生产成本和难储存性，其并未得到大范围应用，故对低温等离子体的深入研究很有必要[2]。低温等离子体有多种产生方法，如电晕放电、介质阻挡放电、滑动电弧放电等[3]。电晕放电的放电温度低，常温、常压下，在发生仓两端加载高压直流电源，对介质气体进行电晕放电，可产生低温等离子体。

在不同研究过程中，因试验对象、条件和方法等因素的差异，最佳放电电压不尽相同。如刘牮等使用直流放电等离子技术与激发过氧化氢气体的方法产生低温等离子体灭菌，放电电压为100～1 000V[4]。刘坤等人设计的线-筒型大气压直流放电装置产生的电压约4kV，可较好地离子化甲酸、乙酸、苯酚等物质[5]。廖瑞金等则在6kV电压下进行了棒-板电极直流放电过程的研究，提出了基于流体力学模型的电晕放电混合数值改进模型[6]。

为了深入研究放电电压、极间距、电导率和介质等因素对产生低温等离子体的影响，需设计一种输出精确且能大范围调节、纹波小、负载突变动态特性好的直流电源来进行相应试验。

1　电源原理与结构

电源主要分为两个部分。第一部分为功率电路，第二部分为反馈控制电路。采用BUCK电压反馈全桥逆变升压整流，作为可调高压直流电源的功率电路拓扑结构。反馈电压在输出端由电压传感器采样，对采样值与参考电压进行比较后输至补偿器；补偿信号输入PWM发生器后改变占空比，以调节BUCK电路输出，完成闭环控制。图1为可调高压直流电源结构框图。

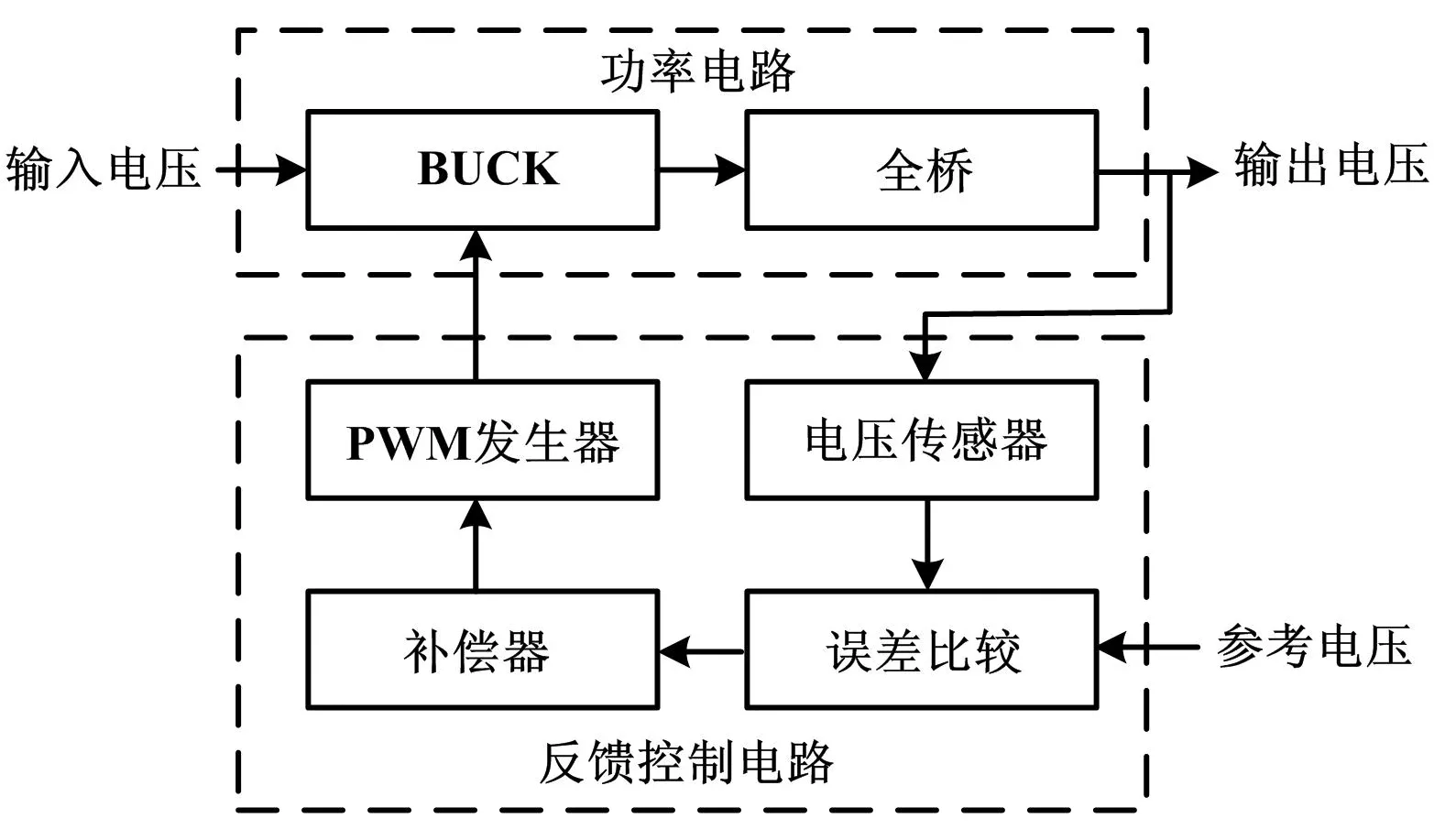
图1　电源结构框图

2　小信号建模

为使输出电压能快速、准确、稳定地追踪参考电压，需设计补偿环节，以提高电源启动时对参考信号的跟踪性能和负载动态变化时的稳定性，并降低稳定输出时的纹波系数。

对可调高压直流电源各环节进行小信号建模，可得到各环节的传递函数，并进行环路分析。Uref(s)表示输入的参考电压信号，U0(s)表示输出电压，Gc(s)表示补偿网络的传递函数，Gm(s)表示PWM发生器的传递函数，Gud(s)表示功率级由输入占空比d(s)到输出电压U0(s)的传递函数，H(s)表示包括电压采样传感器与光耦隔离的反馈环节传递函数。

可调高压直流电源的开环增益为G(s)=Gc(s)Gm(s)Gud(s)，反馈增益为H(s)，环路增益为G(s)H(s)，则系统闭环传递函数为：

(1)

通过绘制环路增益G(s)H(s)的幅频图和相频图，研究相位裕度和增益裕度，即可判断该系统的稳定性，并进行补偿设计。

2.1功率电路

基于BUCK电压反馈全桥逆变升压模式的可调高压直流电源功率电路拓扑[8]如图2所示。

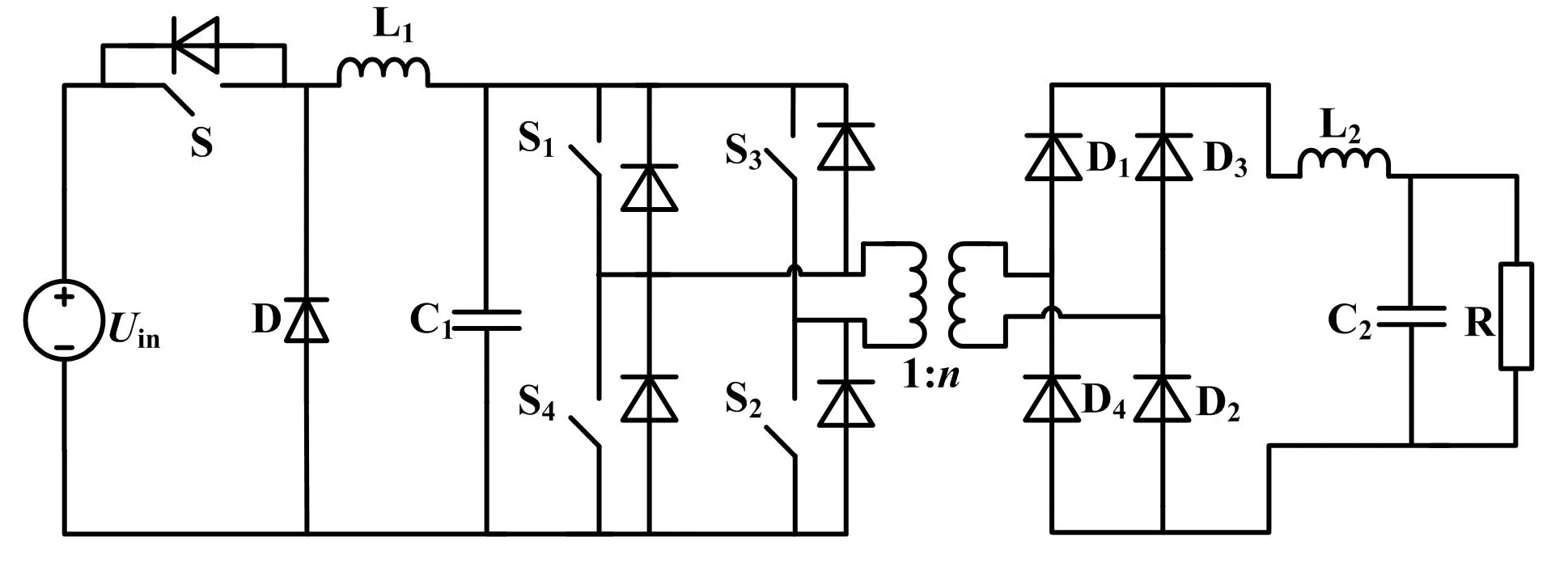
图2　功率电路拓扑图

Uin为市电经整流滤波后得到的约为300 V的直流电压。BUCK级为电压反馈模式，开关管S的占空比d由从负载R两端采样的电压决定。BUCK级的输出电压即为全桥级的输入电压。全桥级各开关管(S1、S2、S3、S4)的占空比D0固定，对角管(S1与S2、S3与S4)同时开闭，并设置一定死区防止S1与S4(或S2与S3)同时导通短路。升压变压器变比为1∶n。

①BUCK级。

由开关管S产生方波电压uin，其平均值与输入电压Uin的关系为:

uin=dUin

(2)

根据基尔霍夫电压定律和电流定律，得：

(3)

(4)

②全桥级。

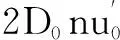
根据基尔霍夫电压定律和电流定律，得：

(5)

(6)

对式(2)～式(6)进行拉普拉斯变换，得到式(7)～式(11)，如下所示：

ui(s)=d(s)Uin

(7)

SL1iL1(s)+[sL2iL2(s)+u0(s)]/2D0n=uin(s)

(8)

(9)

(10)

iL2(s)=C2su0(s)+u0(s)/R

(11)

根据式(7)～式(11)，可得到Gud(s)，即功率电路从占空比d(s)到输出电压u0(s)的传递函数：

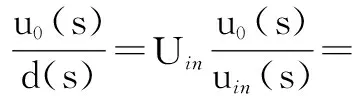
(12)

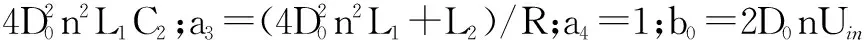
2.2采样与光耦隔离

使用低温漂大电阻串联分压采样，分压采样后使用线性光耦隔离，可分离功率级和控制级电压。两个环节均为线性环节，因此输出电压u0与反馈电压B为线性关系，传递函数为:

(13)

2.3PWM发生器

PWM发生器等效于一个负端输入锯齿波。当正端输入补偿后的电压信号Uc(s)，则输出占空比为d的矩形波。输入电压信号Uc(s)最小为0，最大为锯齿波峰值Um。当正端输入电压信号Uc(s)在0～Um之间变化时，输出PWM波占空比d在0～1之间变化。PWM发生器的传递函数为:

(14)

3　补偿设计

为改善系统频率特性，需在环路中设计补偿环节。首先明确补偿的目的——即理想的伯德图中应当体现充足的相位裕量、足够的带宽和较高的增益。

由奈奎斯特稳定性判据可知，当相位裕量大于0时，系统稳定。在此基础上，若相位裕度很小，则系统处于临界稳定状态，很小的扰动就能导致系统不稳定；若相位裕度过大，系统阻尼很大，会造成系统动态响应变慢，出现过阻尼特性。为了得到满意的性能，相位裕度一般为45°～60°。

带宽由穿越频率决定。穿越频率越大，带宽越大。设计穿越频率时，主要考虑开关频率大小。

由奈奎斯特采样定理可知，若采样频率大于2倍最大信号频率，则采样信号能完整保留原始信号；若采样频率小于2倍最大信号频率，则采样信号无法重构原始信号。

在开关电源中，开关频率会在输出纹波中呈现，必须在环路中加以抑制；否则输出会出现高频噪声和谐波，并导致系统不稳定。因此，穿越频率必须小于开关频率的1/2。工程应用中，一般选择的穿越频率小于开关频率的1/10。

静态增益为频率趋于0时的增益值，它关系到系统的稳态误差。为保证输出精度，系统的稳态误差应较小。当给予阶跃信号时，0型系统的稳态误差为1/(1+|Gud(0)|)，静态增益越小，稳态误差越大；而I型及以上系统的稳态误差为0。

电路各元件的主要参数为：Uin=300、Um=5、n=30、D0=0.49、k=1/1 000、R=36 kΩ、L1=2 mF、C1=2.5 μF、L2=40 mF、C2=0.5 nF。

将除反馈环节Gc(s)外的其余各环节相乘，得到原始环路增益:

G0(s)=Gud(s)H(s)Gm(s)

(15)

式中：H(s)=1/1 000;Gm(s)=1/5。

(16)

(17)

使用Matlab绘制补偿前的原始环路增益G0(s)的伯德图，如图3所示。

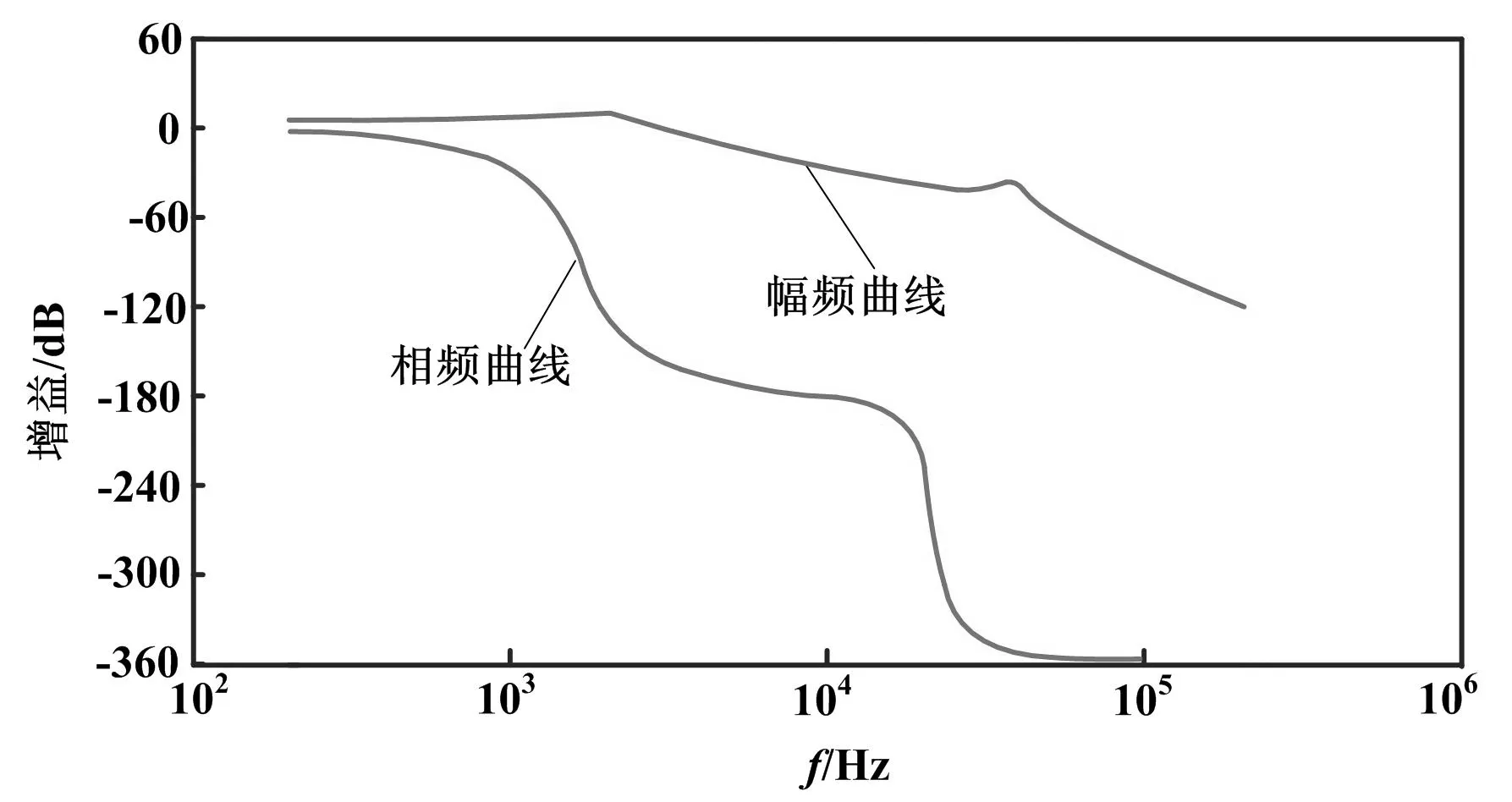
图3　补偿前环路增益伯德图

由图3可以得出以下结论：

①低频段是0型系统，静态增益过小，仅5dB，会导致很大的稳态误差；

②系统穿越频率约3.3kHz，小于开关频率100kHz的1/10，可以抑制高频开关频率引起的谐波和寄生振荡。穿越频率相对较小，可适当增大以占据足够带宽，从而满足系统快速响应的性能要求；

③穿越时，幅频曲线斜率为-40dB/dec，相移接近-180°，相位裕度不足，系统不稳定。

基于以上分析，需设计补偿环节改善原系统性能，调整如下：

①为减小稳态误差，在低频段采用-20dB/dec补偿；

②为调整系统的快速响应性能，可将穿越频率调高，但考虑到幅频曲线38kHz处存在尖峰，穿越频率不能过大，经过权衡，将穿越频率设置为6kHz；

③为保证足够的相位裕度，在穿越时的中频段采用+20dB/dec补偿。

双零-单极补偿器传递函数为:

(18)

为实现以上调整，本文拟采用双零-单极补偿器，其电路结构图如图4所示。

图4　双零-单极补偿器结构图

将补偿器转折频率分别设置在2kHz和3kHz处。通过调整补偿器增益，将系统的穿越频率调整到6kHz。经过计算，得到补偿器各元件参数理论值(为与前文主电路中的C1、C2区别，补偿器元件下标以c开头):Rc1=1 kΩ、Rc2=1.78 kΩ、Cc1=53.1 nF、Cc2=44.8 nF。

选择标准元件值:Rc1=1 kΩ、Rc2=1.8 kΩ、Cc1=56 nF、Cc2=47 nF。

得到补偿器传递函数:

(19)

使用Matlab绘制补偿后环路增益Gc(s)G0(s)的伯德图，如图5所示。

图5　补偿后环路增益伯德图

由图5可以得出以下结论：

①低频段以-20dB/dec下降，稳态误差为0；

②穿越频率按照设计调整至6kHz；

③当系统穿越频率为6kHz时，相位裕度约为58°，位于45°～60°的理想相位裕度范围内。

采用双零-单级补偿器之后，系统性能得以改善，其快速性、准确性和稳定性得以保证。

4　输出仿真

按照计算结果，使用Saber对输出仿真，验证以上补偿设计的效果。

在Saber中建立仿真试验电路，观察输出补偿后的动静态特性，并分析仿真结果[9-10]。设置仿真时间为50ms，步长为100ns。

4.1输入阶跃响应

测试不同参考电压Uref下的输出响应。对Uref分别输入0V、2V、4V、6V、8V和10V阶跃信号，输出电压如图6所示。

图6　输出电压仿真图

当Uref为10V时，BUCK开关管S始终导通，等价于输入电压Uin直接加载在全桥输入端。电源输出电压最高只能达到8 820V，不能达到100Uref=10 000V。当Uref为0V、2V、4V、6V和8V时，稳定后可分别输出0V、2kV、4kV、6kV和8kV，即得到1 000Uref的电压，实现输出电压对参考信号Uref的渐近跟踪；但当Uref为0V时，输出存在较大超调量。同时，考虑到线性光耦在宽输出范围内的非线性，可将参考电压限定在1～8V范围，此时输出电压为1～8kV，调节时间为10～20ms。

4.2纹波

输出电压范围为1～8kV，分别选择在最小值1kV、中间值4.5kV以及最大值8kV三个输出电压处测试输出纹波，对应的Uref分别为1V、4.5V和8V，负载R为36kΩ。

输出电压稳态纹波如图7所示。

图7　输出电压稳态纹波图

当输出电压为1kV时，纹波的峰-峰值Upp约为8V，纹波系数为:

Y=UPP/U=0.8%

(20)

当输出电压为4.5kV时，纹波的峰-峰值UPP约为35V，纹波系数为:

Y=UPP/U=0.78%

(21)

当输出电压为8kV时，纹波的峰-峰值UPP约为40V，纹波系数为:

Y=UPP/U=0.5%

(22)

因此，在1～8kV范围内，该电源纹波系数≤1%。较小的纹波系数可以保证直流电晕放电试验不受高频噪声和谐波干扰，从而取得较好的试验效果。

4.3负载动态变化

同样地，选择在最小值1kV、中间值4.5kV以及最大值8kV三个输出电压处，测试负载突变时的电压动态变化。当负载电阻36kΩ下的输出达到稳态后，在30ms时将其切换至20kΩ，观察输出动态变化过程，如图8所示。

图8　负载突变时输出动态变化图

由图8可知，各输出电压在负载突变瞬间突然下降，在反馈回路的调节下，经轻微的震荡后很快又恢复到了目标输出电压。从一个稳态工作点到达下一个稳态工作点，动态响应速度快、过冲小、振荡少。

电晕放电试验时出现的电离、火花或击穿等现象，会突然改变负载大小。在负载变化时，输出电压稳定在目标值，可以保证直流电晕放电试验的效果。

5　结束语

为开展电晕放电产生低温等离子体的研究试验，

本文设计了一种可调高压直流电源[7-10]。其采用BUCK电压反馈和全桥逆变升压模式，实现可调高压直流输出。本文详细阐述了系统各环节的小信号建模过程，得到系统原始的环路传递函数。针对其静态增益小和相位裕度不足等问题，采用双零-单极补偿器补偿。其频率特性得到改善，消除了静态误差，相位裕度约为58°。Saber仿真结果表明，输出电压可以在1～8kV范围内快速、准确、稳定地渐近跟踪1～8V参考信号；同时，输出交流成分少，纹波系数小于1%，负载切换时动态特性好。可调高压直流电源，可为电晕放电产生低温等离子体的研究试验提供便利、可靠的试验条件。

[1]NUNEZCM,RAMSEYGH,PONDERWH,etal.Coronadestruction:aninnovativecontroltechnologyforVOCsandairtoxics[J].Air&Waste,1993,43(2): 242-247.

[2]RAHMANF,CHUNBJ,LEEKS,etal.Effectoftemperatureontheperformancecharacteristicsofapin-cylinderdischargetypeozonizer[J].KieeInternationalTransactionsonElectrophysics&Applications,2002,2(4):201-207.

[3] 杜长明,李俊岭,严建华.滑动弧放电等离子体去除甲苯的实验研究[J].高电压技术,2008,34(3): 512-516.

[4] 刘牮,张网军.直流辉光放电低温等离子灭菌装置的研制[J].中国消毒学杂志,2010,27(5):549-551.

[5] 刘坤,廖峥,侯世英.大气压直流辉光放电装置的实验与分析[J].重庆大学学报,2013,36(3):71-76.

[6] 廖瑞金，刘康淋，伍飞飞，等.棒-板电极直流负电晕放电过程中重粒子特性的仿真研究[J].高电压技术,2014,40(4):965-971.

[7]ERICKSONRW,MAKSIMOVICD.FundamentalsofPowerElectronics[M].NewYork:SpringerScience&BusinessMedia,2001.

[8] 洪悦.30kV可调直流高压电源设计[D].大连: 大连理工大学,2011.

[9]CHENCT.LinearSystemTheoryandDesign[M].NewYork:OxfordUniversityPress,1995.

[10]DORFRC,BISHOPRH.ModernControlSystems[M].NewYork:Pearson,2011.

AdjustableHighVoltageDCPowerSupplyUsingBUCKVoltageFeedbackFull-bridgeBoostInversion

Forcarryingoutrelevantresearchandexperimentoflowtemperatureplasma,theadjustablehighvoltageDCpowersupplyisdesignedbyusingBuckvoltagefeedbackfullbridgeboostinversiontopology.Inordertoschievefasttrackingforoutputofpowersupplyuponthereferencesignal,modelingofthesmallsignalforeachmoduleofthecircuitisconducted,thetransferfunctionofsystematicloopgainisbuilt.ThesatbilityoforiginalsystemisanalyzedbyadoptingMatlab,andcompensatedusingdouble-zerosinglepolecompensator.ThecircuitaftercompensationissimulatedwithSaber,toverifythestaticindexesanddynamiccharacteristicsofthecompensatedcircuit.Theresultsshowthattheoutputofpowersupplycanasymptoticallytrackthegivenreferencesignal,andoffersgooddynamiccharacteristics,thusthepowersupplycanbeappliedinexperimentalresearchonlowtemperatureplasmer.

Low-temperatureplasmaAdjustablehighvoltageDCpowersupplySensorBUCKcircuitPulsewidthmodulation(PWM)SaberCompensationMatlab

徐晨剑(1992—)，男，现为同济大学控制科学与工程专业 在读硕士研究生；主要从事开关电源和工业自动化方向的研究。

TH86;TP17

ADOI:10.16086/j.cnki.issn1000-0380.201609007

修改稿收到日期：2015-01-17。