形状任意的超材料电磁隐身波长变换器的设计

刘冶，李竹影，俞翔，曹文康，赵亚（海军工程大学，武汉 430033）

形状任意的超材料电磁隐身波长变换器的设计

刘冶，李竹影，俞翔，曹文康，赵亚
（海军工程大学，武汉 430033）

目的 研究形状任意的超材料电磁隐身波长变换器的设计方法。方法 基于坐标变换理论，通过对空间中的不同区域先后进行压缩和扩张变换，设计出该装置不同区域的电磁参数张量。结果 一方面，入射波经过该装置时，在其界面不产生散射，并且入射波穿过装置进入外部自由空间时又能恢复其初始传播状态；另一方面，该装置在特定区域改变了电磁波的波长。结论 有限元软件的仿真结果显示波长变换器实现了预期的电磁功能，从而验证了该装置电磁参数张量表达式的正确性。

超材料；坐标变换；波长变换器；隐身

人工超材料实现了自然材料并不具备的奇异物理性能，除了负折射、逆多普勒效应、完美透镜、逆Cerenkov辐射效应等反常物理特性[1]外，而以坐标变换理论[2—3]为基础的超材料[4]在理论上可实现对电磁波的完美隐身。自Schurig等人在2006年完成了世界上第一个简化参数的圆柱形电磁隐身斗篷的参数设计和微波仿真验证[4]后，基于坐标变换理论来设计电磁隐身斗篷及其拓展装置的研究很快成为超材料领域的又一个重要研究方向。除了隐身斗篷[5—11]，人们应用坐标变换理论还设计了电磁聚焦器[12]、电磁弯折器[13]、规则形状的波长变换器[14]、波形转换器[15]等多种功能型超材料电磁装置。

在超材料装置的研究中，某课题组先后推导出了圆柱形和椭圆柱形波长变换器的电磁参数张量，发展了新型超材料波长变换器的设计方法[14]。在此基础上，文中将波长变换器的构型拓展到任意形状，推导了任意形状波长变换器的电磁参数张量，使波长变换器在构型设计上的更灵活。

1　电磁参数张量的推导

文中仅讨论如何用波长变换器来放大电磁波的波长，对波长缩小的讨论同理。在设计波长变换器时需要进行两次空间变换，第一次变换是将原空间中的某一部分区域进行压缩，即将图1a中的区域II，III压缩成如图1b所示的区域III，以实现入射波的无散射传播；第二次变换是将原空间中剩下的区域I扩张成如图1c所示的区域II′，以使得装置可以放大入射电磁波的波长。

1.1空间压缩

图1为形状任意的波长变换器的二维构型，该构型由三条任意的共形曲线组成。设曲线的归一化边界方程为R（0θ），按照从内到外的顺序，图1中三条封闭曲线的方程依次为aR（0θ），bR（0θ），cR（0θ），a，b，c为比例系数。则有区域I为0≤r（θ）≤aR0（θ），区域II为aR（0θ）＜r（θ）≤bR（0θ），区域III 为bR（0θ）＜r（θ）≤cR（0θ），区域II′为0＜r（θ）≤bR（0θ）。图1b表示的压缩过程，对应的坐标变换式为：

图1　形状任意的波长变换器的空间变换过程Fig.1　Procedures of space transformations in designing of the invisible wavelength transformer with arbitrary shape

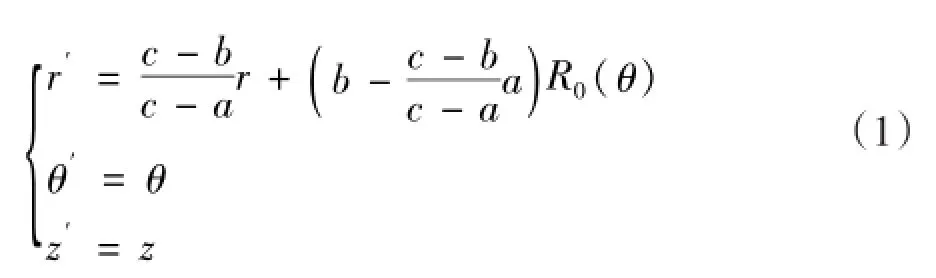
如果令c=1，cR（0θ）=R（0θ）是该波长变换器的外边界曲线方程，此时a，b转化为R（0θ）所围区域的压缩系数，可令a=n，b=m，并设：

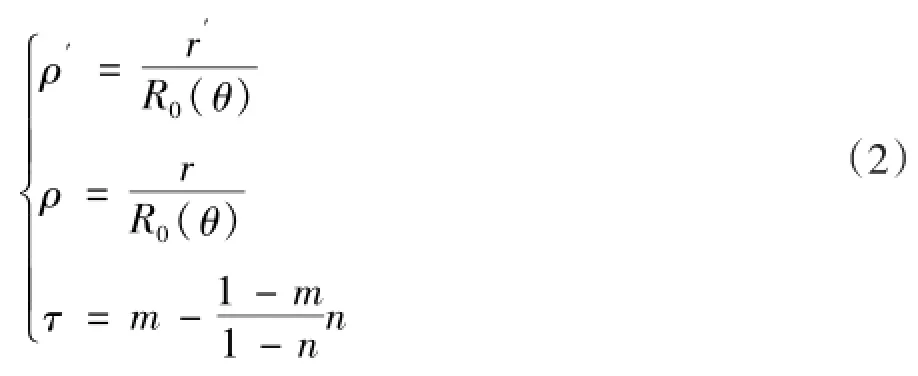
可以得到：

在直角坐标系中：

由式（2）—（4）以及三角函数的定义可以得到：

由式（5），根据坐标变换理论[2，6]，可以推导出波长变换器中空间压缩区域的电磁参数张量分别为：

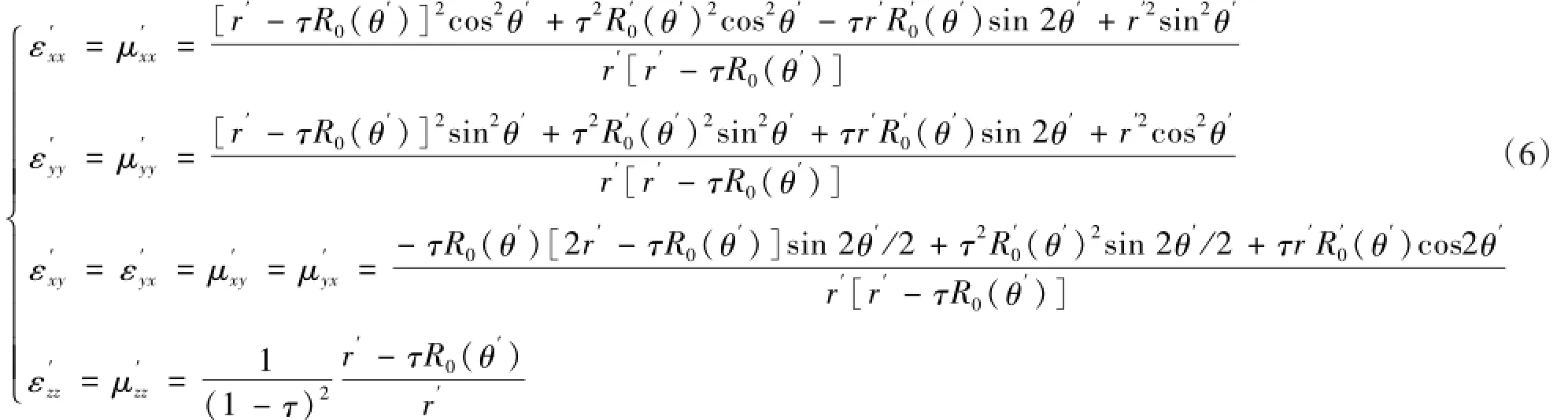
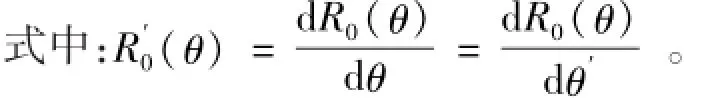
1.2空间扩张

在压缩过程后，为满足变换空间的连续性，需要将原空间中的区域I扩张至区域II′，如图1c所示。该扩张过程对应的坐标变换式在直角坐标系下可写为：

根据坐标变换理论，可以很快得到波长变换器在该区域的电磁参数张量为：

2　建模与仿真

任意形状波长变换器的仿真模型如图2所示。

图2　任意形状波长变换器的仿真模型Fig.2　The sketch map of simulation model of the invisible wavelength transformer with arbitrary shape

在图2中，取压缩系数m=0.6，n=0.3，并设波长变换器的归一化曲线方程为R0（θ）=0.04·（cos 2θ+ sin 3θ+cosθ+3）。采用基于有限元的COMSOL Multiphysics商业仿真软件进行数值仿真计算。仿真条件中，波源为单位强度的TM平面波，工作频率为10 GHz，矩形求解域为0.45 m×0.36 m，求解域的四周设置为吸收边界，波长变换器的各个边界均为连续边界，TM波从矩形域的左边界垂直入射。最终的仿真结果如图3所示。

图3　任意形状波长变换器的磁场分布Fig.3　The magnetic field distribution of the invisible wavelength-transformer with arbitrary shape

从图3中可知，当TM波传播至波长变换器的压缩区域III时，其等相位面开始平滑地沿着装置的扩张区域II′的边界弯曲，而当TM波传播至扩张区域II′的内部时，TM波的波长明显被放大，并且该入射波在扩张区域传播时并没有出现散射和反射的现象。当TM波从波长变换器内部透射至外部自由空间时，其等相位面又恢复到原来的入射波形态。如果从外部自由空间来观测TM波传播的情况，则会发现TM波好像一直处于初始状态，说明波长变换器的存在不影响TM波在该装置外部的传播方式。从图3中可以看到，形状任意的波长变换器同时具备对电磁波隐身和变换电磁波波长的功能，该结果也验证了式（6）和（8）的正确性。

文中从数值仿真计算的结果中还提取了波长变换器外部自由空间区域和内部扩张空间区域的场强变化图，并比较了这两区域中的电磁波波长，如图4所示。图4a为自由空间区域，TM波的波长为0.03 m，传播过程中一直保持不变；图4b为波长变换器的扩张空间区域，TM波的波长为0.06 m，恰为自由空间中波长的2倍，这个放大倍数正好就是图1c中扩张区域II′的扩张倍数，也是波长变换器在建模过程中比例系数b相对于a的倍数。因此，图4的仿真计算结果再一次验证了任意形状波长变换器的理想隐身和变换入射波波长的电磁功能。

图4　求解域不同区域的场强变化Fig.4　Diagram of field density in different regions of solution domain

3　结语

应用坐标变换理论，设计出了同时具备对电磁波隐身和变换入射电磁波波长等功能的形状任意的超材料电磁隐身波长变换器，推导出了波长变换器不同区域的电磁参数张量表达式，并采用有限元仿真软件对该装置的电磁特性进行数值仿真，仿真结果显示所设计的波长变换器完全实现了上述电磁功能，从而验证了该装置电磁参数张量推导的正确性。关于该装置的设计方法不仅增加了超材料电磁隐身波长变换器在构型设计上的灵活性，还拓展了坐标变换理论在设计超材料隐身电磁装置上的应用。

[1]SHELBY R A，SMITH D R，SCHULTZ S.Experimental Verification of a Negative Index of Refraction[J].Science，2001，292（5514）：77—79.

[2]SCHURIG D，PENDRY J B，SMITH D R.Calculation of Material Properties and Ray Tracing in Transformation Media[J]. Optics Express，2006，14（21）：9794—9804.

[3]PENDRY J B，SCHURIG D，SMITH D R.Controlling Electromagnetic Fields[J].Science，2006，312（5781）：1780—1782.

[4]SCHURIG D，MOCK J J，JUSTICE B J，et al.Metamaterial Electromagnetic Cloak at Microwave Frequencies[J].Science，2006，314（5801）：977—980.

[5]WU Q，ZHANG K，MENG F Y，et al.Material Parameters Characterization for Arbitrary N-sided Regular Polygonal Invisible Cloak[J].J Phys D：Appl Phys，2009，42：035408.

[6]LI C，LI F.Two-dimensional Electromagnetic Cloaks with Arbitrary Geometries[J].Optics Express，2008，16（17）：13414—13420.

[7]MA H，QU S B，XU Z，et al.Material Parameter Equation for Elliptical Cylindrical Cloaks[J].Phys Rev A，2008，77（1）：013825.

[8]刘冶，李竹影，张旺洲，等.组合型电磁隐身斗篷的超材料设计与仿真[J].功能材料，2013，44（15）：2235—2238.

LIU Ye，LI Zhu-ying，ZHANG Wang-zhou，et al.Design and Emulation of Combined-shaped Electromagnetic Stealthy Cloak Made of Metamaterials[J].Journal of Functional Materials，2013，44（15）：2235—2238.

[9]刘冶，李竹影，赵林，等.一种无奇异参数椭圆形电磁隐身斗篷的设计基础理论[J].装备环境工程，2015，12（1）：6—10.

LIU Y，LI Zhu-ying，ZHAO Lin，et al.A Design Fundamental Theory of Elliptic Cylindrical Invisible Cloak with Non-singular Electromagnetic Tensors[J].Equipment Environmental Engineering，2015，12（1）：6—10.

[10]JIANG W X，CUI T J，YU G X，et al.Arbitrarily Elliptical-cylindrical Invisible Cloaking[J].J Phys D：Appl Phys，2008，41 （8）：085504.

[11]CHEN H S，ZHENG B，SHEN L，et al.Ray-optics Cloaking Devices for Large Object in Incoherent Natural Light[J].Nature Communications，2013（4）：2652.

[12]YU G X，JIANG W X，ZHOU X Y，et al.Non-rotationally Invariant Invisibility Cloaks and Concentrators of Em Wavesz [J].Eur Phys J Appl Phys，2008，44：181—185.

[13]JIANG W X，CUI T J，ZHOU X Y，et al.Arbitrary Bending of Electromagnetic Waves Using Realizable Inhomogeneous and Anisotropic Materials[J].Phys Rev E，2008，78（6）：066607.

[14]刘冶，李竹影，张旺洲，等.超材料电磁隐身波长变换器的设计与仿真[J].功能材料，2014，45（11）：11027—11031.

LIU Ye，LI Zhu-ying，ZHANG Wang-zhou，et al.Design and Simulation of Metamaterial Electromagnetic Invisible Wavelength-transformer[J].Journal of Functional Materials，2014，45（11）：11027—11031.

[15]MA H，QU S B，XU Z，et al.General Method for Designing Wave Shape Transformers[J].Opt Express，2008，16（26）：22072—22082.

Design of Metamaterial Electromagnetic Invisible Wavelength Transformer with Arbitrary Shape

LIU Ye，LI Zhu-ying，YU Xiang，CAO Wen-kang，ZHAO Ya
（Naval University of Engineering，Wuhan 430033，China）

Objective To study the design method of metamaterial electromagnetic invisible wavelength transformer with arbitrary shape.Methods Based on coordinate transformation theory,by means of compressing certain region and then expanding another one in the space,the electromagnetic tensors of the device in different regions were deduced.Results On one hand,when the incoming waves propagated into the device,there was no scattering on the boundary of the device.And the waves returned to their original propagation when they propagated into the free space from the inner region of the device.On the other hand,the device could change the wavelength of electromagnetic wave in the particular region.Conclusion The simulation results of the software based on finite element method showed that the wavelength transformer realized the anticipated electromagnetic function,which validated the electromagnetic tensor expressions of the device.

metamaterial；coordinate transformation；wavelength-transformer；invisibility

2015-07-07；Revised：2015-08-09

10.7643/issn.1672-9242.2016.01.018

TJ99；TM25

A

1672－9242（2016）01－0098-04

2015-07-07；

2015-08-09

国防预研基金项目（9140A270304）

Fund：Supported by the National Defense Pre-research Foundation（9140A270304）

刘冶（1986—），男，湖北武汉人，博士，工程师，主要研究方向为超材料隐身装置的构型设计与性能优化。

Biography：LIU Ye（1986—），Male，from Wuhan，Hubei，Ph.D.，Engineer，Research focus：configuration design and property optimization of metamaterial invisible device.