基于Backstepping的严格反馈极值搜索系统控制器设计

张　雷，胡云安，张　杨，王佩飞

（海军航空工程学院a.控制工程系；b.研究生管理大队，山东烟台264001）

基于Backstepping的严格反馈极值搜索系统控制器设计

张雷a，胡云安a，张杨a，王佩飞b

（海军航空工程学院a.控制工程系；b.研究生管理大队，山东烟台264001）

针对一类含不确定参数的严格反馈型极值搜索系统的控制问题，将极值搜索方法和反演（Backstepping）控制方法相结合，设计出系统状态的极值参考轨迹，利用Backstepping控制方法逐步递推选取适当的Lyapunov函数设计控制器和不确定参数自适应估计律，实现目标函数的极值搜索。仿真表明所提出控制器设计方法的有效性。

严格反馈；不确定参数；极值搜索系统；自适应估计律

实际控制系统中，系统的参考输出量与输入量之间通常可以构成某种未知的参考轨迹，这种参考轨迹关系意味着在参考输入的作用下，系统的输出轨迹中存在一个全局最优输出值（极大值或者极小值）［1-2］。面对实际的极值搜索被控对象，有时很难准确而完整地掌握和分析它结构和机理，这不可避免地导致了系统模型建立的不够准确；同时，考虑到系统参数可能存在的不确定性等因素影响，最终导致研究人员很难准确地知晓系统的参考轨迹形式并实现未知参考轨迹的寻优［3-4］。长期以来，人们为了能够找到实现未知参考轨迹寻优的方法进行了不断的探索。这些寻优方法被统称为最优化方法，或者优化方法，已发展比较成熟的方法如粒子群方法［5-6］、遗传方法［7］、模拟退火方法［8］等方法都具有较好的搜索效果，但这些方法都是从数值计算的角度去解决寻优问题，且要求系统的参考轨迹是已知或至少部分已知的。如何从控制的角度采用适当的控制方法，在实际系统的参考轨迹不能确定的情况下，仍能够使得系统的输出量自适应地收敛并稳定于输出量的全局最优输出值，从而使控制过程中期望的控制目标最优化，这是控制界学者一直致力于解决的一类问题，而极值搜索方法首次从控制的角度解决了未知参考轨迹的寻优问题［9］。文献［10］针对一类含不确定参数的极值搜索系统的控制问题，设计最优控制器，使目标函数沿期望状态轨迹收敛至其对应的函数极值。文献［11］针对多变量参数不确定极值搜索系统进行了控制器设计，保证了系统的稳定性。

20世纪90年代初，Kanellakopoulos［12］首次提出了反演（Backstepping）控制方法，在逐步递推的设计过程中引入虚拟控制量的概念，并基于Lyapunov稳定性理论给出了控制器的设计过程。对于严格反馈非线性系统而言，自适应Backstepping［13］能够在参数未知的情况下得到很强的稳定性结论，而鲁棒自适应backstepping控制则能够处理模型中存在不确定项和外部干扰的情况。对于确定的严格反馈非线性系统，利用传统的Backstepping控制器便可得到全局渐近稳定的结论，Yao等［14-15］将自适应技术与Backstepping控制方法相结合，解决了具有参数不确定性的严格反馈非线性系统的控制问题，Wang［16］，Zhang［17］，Polycarpou［18］等分别利用神经网络对系统中的未知非线性函数进行估计，解决了含有未知函数的严格反馈非线性系统的控制问题，以上文献都为本文Backstepping控制器设计提供了参考。

本文针对一类含不确定参数的严格反馈型单输入极值搜索系统的极值搜索问题，将极值搜索方法和Backstepping控制方法相结合，设计出能使目标函数搜索到极值的极值参考轨迹；利用Backstepping控制方法，逐步递推选取适当的Lyapunov函数进行控制器设计。仿真表明了所设计的不确定参数自适应估计律能实现本文的控制目标。

1　问题描述

考虑如下形式的一类含不确定参数的严格反馈型单输入极值搜索系统：

假设1：目标函数y=J（x1，θ）存在唯一极值点，且对应的系统状态量满足：

本文将设计自适应估计律对不确定参数θ进行估计，对式（3）进行微分可得：

由式（4）可得状态量x1的参考轨迹x1，d应满足

式中，kd∈ℝ+为设计常数。

将式（5）代入式（4）可得

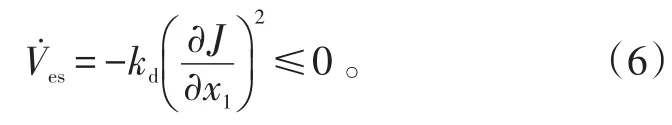
由式（3）可得Ves≥0成立且仅在时存在Ves=0。由式（4）可得极值参考轨迹x1，d如式（5）所示时成立且仅在时存在。当状态量x1将沿着极值参考轨迹x1，d向着使的方向趋近时，最终可达到对应的极值点处，此时目标函数取得极值。

控制目标：目标函数搜索到其对应的极值处，闭环系统中的所有信号有界。

目标函数搜索其对应极值的过程即是状态量准确跟踪极值参考轨迹且不确定参数量被准确估计的过程。

假设2：极值参考轨迹 x1，d及其高阶导数为有界光滑函数。

假设3：存在常数 T0、μ0＞0对于函数向量存在

2　基于Backstepping的控制器设计

采用Backstepping技术对预设性能控制器进行设计，不确定参数θ的估计误差为，通过自适应方法对不确定参数进行估计。以n=3为例，控制系统原理框图如图1所示。

第1步：考虑系统（1）中的第1个子系统，设不确定参数θ的估计误差为，构造Lyapunov函数，对V1求一阶导数可得：

针对式（8）设计x2的虚拟轨迹：

式中，k1＞0为设计参数。

由式（8）、（9）可得：

式中，z2=x2-x2，d。

当x2能够准确跟踪x2，d时，即z2趋近于0。

图1　当n=3时控制系统原理框图Fig.1 Block diagram of control system forn=3

第2步：考虑系统（1）中的第2个子系统

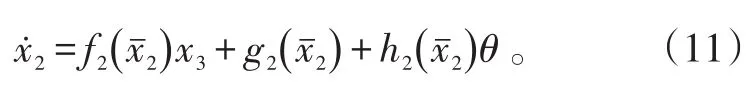
针对式（12）设计x3的虚拟轨迹

式中，k2＞0为设计参数。

定义z3=x3-x3，d，由式（12）、（13）可得：

第3步：考虑系统（1）中的第3个子系统

针对式（16）设计x4的虚拟轨迹

式中，k3＞0为设计参数。

定义z4=x4-x4，d，由式（15）、（16）可得

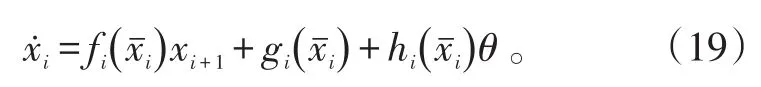
针对式（20）设计xi+1的虚拟轨迹

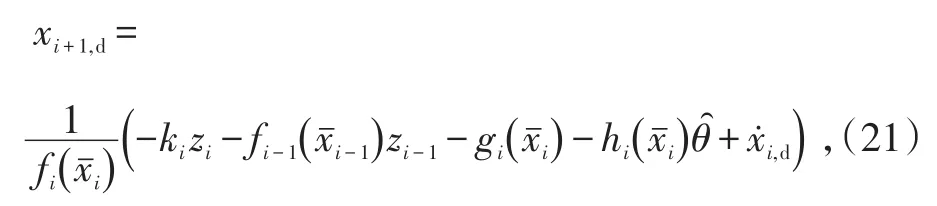
式中，ki＞0为设计参数。

定义zi+1=xi+1-xi+1，d，由式（19）、（20）可得：

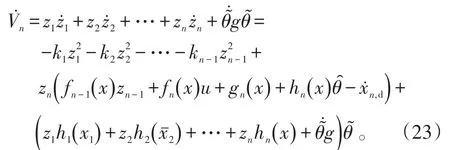
参考式（23），设计实际控制量和参数估计律分别为：

式（24）、（25）中：kn＞0为设计参数；。

将参考Backstepping方法设计的控制输入量式（24）和自适应估计律式（25）代入式（23）可得：

定理1：考虑系统（1）所描述的一类参数不确定严格反馈非线性系统，在假设1～4成立的前提下，采用极值参考轨迹如式（5）所示，虚拟控制器设计如式（21）、（22）所示，实际控制输入量如式（24）所示，自适应估计律如式（25）所示，可以得到如下结论：

1）目标函数J（x1，θ）搜索到其对应的极值处；

2）系统（1）是渐进稳定的且闭环系统中的所有信号有界。

需要特别强调的是，对于极值参考轨迹x1，d设计中的关于目标函数的导数和计算过程中所用到的虚拟控制量导数，采用解析法进行求解。

3　仿真分析

针对如下对象进行仿真分析，数学模型如下：

式（27）中：x1、x2为系统状态变量；θ=1为不确定参数；为目标函数，具有全局极大值

参考式（5）设计状态量x1的极值参考轨迹x1，d为：

采用本节所设计的Backstepping控制方法进行仿真分析，系统的状态变量初始值分别为，参数估计初始值为，极值参考轨迹 x1，d初始值为。控制器参数：g=2， kd=1，k1=2，k2=4。仿真结果如图2～8所示。

图2　目标函数J（x1，θ）仿真图Fig.2 Simulation result of objective functionJ（x1，θ）

图3　不确定参数估计值仿真图Fig.3 Simulation result of uncertain parameter estimated value

图4　状态变量x1和极值参考轨迹x1，d仿真图Fig.4 Simulation result of state variablex1and extremum reference trajectoryx1，d

图5　状态变量x1跟踪误差z1Fig.5 Simulation result of state variablex1tracking errorz1

图6　状态变量x2和参考轨迹x2，d仿真图Fig.6 Simulation result of state variablex2and reference trajectoryx2，d

图7　状态变量x2跟踪误差z2Fig.7 Simulation result of state variablex2tracking errorz2

图8　控制输入量u仿真图Fig.8 Simulation result of control inputu

由图2可知：设计的极值参考轨迹x1，d有效，目标函数能够准确收敛至全局极大值处；由图3可知：设计的估计律能够准确估计不确定参数；由图4、5可知：状态量x1能够准确跟踪极值参考轨迹x1，d最终收敛至处；由图6、7可知：状态量x2能够准确跟踪极值参考轨迹x2，d；由图8可知：控制输入量u有界。通过仿真分析可知：本文设计的Backstepping控制方法可以实现控制目标且效果较好。

4　结论

本文针对一类含不确定参数的严格反馈型单输入极值搜索系统的极值搜索问题。首先，设计出能使目标函数搜索到极值点的极值参考轨迹；其次，利用Backstepping控制方法逐步递推选取适当的Lyapunov函数进行控制器设计；最后，设计不确定参数的自适应估计律，满足控制目标。仿真验证了本文设计方法可行有效。

［1］KRSTIC M，WANG H H.Stability of extremum seeking feedback for general nonlinear dynamic systems［J］.Automatica，2000，36（4）：595-601.

［2］BLACKMAN B F.Extremum-seeking regulators［C］//An Exposition of Adaptive Control.New York：IEEE，1962：36-50.

［3］ADETOLA V，GUAY M.Parameter convergence in adaptive extremum-seeking control［J］.Automatica，2007，43（1）：105-110.

［4］左斌，胡云安，施建洪.极值搜索算法的研究与进展［J］.海军航空工程学院学报，2006，21（6）：611-617. ZUO BIN，HU YUNAN，SHI JIANHONG.Research and development of extremum seeking algorithm［J］. Journal of Naval Aeronautical Engineering Institute，2006，21（6）：611-617.（in Chinese）

［5］高立群，李若平，邹德旋.全局粒子群优化算法［J］.东北大学学报：自然科学版，2011，32（11）：1538-1541. GAO LIQUN，LI RUOPING，ZOU DEXUAN.A global particle swarm optimization algorithm［J］.Journal of Northeastern University：Natural Science，2011，32（11）：1538-1541.（in Chinese）

［6］雷翻翻，高岳林.约束优化问题的改进粒子群优化算法［J］.兰州理工大学学报，2011，37（4）：84-89. LEI FANFAN，GAO YUELIN.Improved partical swarm optimization algorithm for solving constrained optimization problems［J］.Journal of Lanzhou University of Technology，2011，37（4）：84-89.（in Chinese）

［7］刘庆波，余跃庆.基于遗传算法的欠驱动机器人模糊控制器设计［J］.系统仿真学报，2008，20（8）：2097-2100. LIU QINGBO，YU YUEQING.Fuzzy controller design for under actuated robots based on GA method［J］.Jour-nal of System Simulation，2008，20（8）：2097-2100.（in Chinese）

［8］梁毓明，徐立鸿.基于改进模拟退火混合算法的移动机器人全局路径规划［J］.控制与决策，2010，25（2）：237-240. LIANG YUMING，XU LIHONG.Mobile robot global path planning based modified simulated annealing hybrid algorithm［J］.Control and Decision，2010，25（2）：237-240.（in Chinese）

［9］左斌，李静，胡云安.极值搜索算法研究及其应用［M］.北京：国防工业出版社，2014：1-2. ZUO BIN，LI JING，HU YUAN.Research on extremum seeking algorithm and its application［M］.Beijing：National Defense Industry Press，2014：1-2.（in Chinese）

［10］GUAY M，ZHANG T.Adaptive extremum seeking control of nonlinear dynamic systems with parametric uncertainties［J］.Automatica，2003，39（7）：1283-1293.

［11］SHAKIBA YAGHOUBI，MARYAM DEHGHANI.Adaptive extremum seeking control of a nonlinear system using backstepping technique［C］//23rdIranian Conference on Electrical Engineering.Iranian：IEEE，2015：960-965.

［12］KANELLAKOPOULOS I，KOKOTOVIC P V，MORSE A S.Systematic design of adaptive controllers for feedback linearizable systems［J］.IEEE Transactions on Automatic Control，1991，36（11）：1241-1253.

［13］SETO D，ANNASWAMY A M，BAILLIEUL J.Adaptive control of nonlinear systems with a triangular structure ［J］.IEEE Transactions on Automatic Control，1994，39（7）：1411-1428.

［14］YAO B，TOMIZUKA M.Adaptive robust control of MIMO nonlinear systems in semi-strict feedback forms［J］. Automatica，2001，37（9）：1305-1321.

［15］YAO B，TOMIZUKA M.Adaptive robust control of SISO nonlinear systems in a semi-strict feedback form［J］.Automatica，1997，33（5）：893-900.

［16］WANG D，HUANG J.Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strict-feedback form［J］.IEEE Transactions on Neural Networks，2005，16（1）：195-202.

［17］ZHANG T，GE S S，HANG C C.Adaptive neural network control for strict-feedback nonlinear systems using backstepping design［J］.Automatica，2000，36（12）：1835-1846.

［18］POLYCARPOU M M.Stable adaptive neural control scheme for nonlinear systems［J］.IEEE Transactions on Automatic Control，1996，41（3）：447-451.

Controller Design for Strict-Feedback Extremum Seeking Systems Based on Backstepping

ZHANG Leia，HU Yunana，ZHANG Yanga，WANG Peifeib
（Naval Aeronautical and Astronautical University a.Department of Control Engineering；b.Graduate Students’Brigade，Yantai Shandong 264001，China）

To solve control problems of strict-feedback extremum seeking systems with uncertain parameter，extremum seeking control method and Backstepping control method were combined.System state extremum reference trajectory was designed.Backstepping controller and uncertain parameter adaptive estimation law were designed based on the appropriate Lyapunov functions selected by recurrence method，objective function extremum seeking was realized.Simulation result showed that the proposed controller design method was effectiveness.

strict-feedback；uncertain parameter；extremum seeking systems；adaptive estimation law

TP273+.23

A

1673-1522（2016）04-0401-06

10.7682/j.issn.1673-1522.2016.04.001

2016-05-14；

2016-06-02

国家自然科学基金资助项目（60674090）

张雷（1988-），男，博士生。