非线性系统分数阶滑模控制分析与设计

于昊天，时　宝

（海军航空工程学院基础部，山东烟台264001）

非线性系统分数阶滑模控制分析与设计

于昊天，时宝

（海军航空工程学院基础部，山东烟台264001）

文章对非线性整数阶或分数阶系统，提出了统一的分数阶滑模控制方法。首先，对整数阶控制系统，设计分数阶滑模面，提出分数阶趋近律，通过对倒立摆系统的仿真，验证了该方法的有效性；然后，引入最优控制指标，研究了滑模控制阶次α对控制效果的影响，对于该整数阶系统，控制指标最优时α∉ℤ；最后，将本文方法推广到分数阶系统的控制，通过对分数阶Chen系统的仿真，验证了该方法的有效性，并发现对于该系统控制指标最优时，控制阶次与系统阶次不同元。

非线性控制系统；分数阶系统；分数阶滑模控制；倒立摆；分数阶Chen系统

17世纪，在经典微积分建立不久，分数阶微积分已经初步定义，但是由于缺乏明确物理意义，300多年来并没有引起科学家们足够的关注，其发展也仅停留在理论上，自20世纪60年代，这个尘封已久的概念重新回到了学者们的视野中。尤其是90年代以来，随着科学技术的发展，尤其是航空航天技术、生物学、粘弹性材料研究的发展和应用，分数阶微积分巨大的研究潜力和应用价值引起越来越多的关注，也使其得到了快速的发展［1-2］。

遗传性、自相似性在客观世界物理现象中广泛存在，半导体的例子也许最能说明分数阶模型要比整数阶模型更加准确［3］。与此同时，分数阶控制方法的研究和应用也在最近20年得到了极大的发展。分数阶控制器目前主要有由Oustaloup团队提出的分数阶鲁棒控制器CRONE，现在已有Matlab专门的工具箱［4］；由Podlubny提出的PIλDμ控制器，这也是目前研究比较广泛的方法［5-7］。这些控制方法在模拟仿真和部分应用中，较传统控制方法展示出了一定的优点，如收敛更快，超调量更小，误差更小等等.

近年来，随着非线性理论的发展和工业控制技术的进步，滑模控制方法取得了很对好的研究成果［8-9］。很多学者对机械系统、机电系统、混沌系统等分数阶滑模控制进行了一系列研究［10-20］。文献［10-11，16］设计的控制量中出现了Dα（sgn（s）。文献［13］在一阶微分系统的控制中引入了D1+αe，取得较好的控制效果，但是引入的分数阶微分次数超过原系统的阶次，仍有改进的余地。

1　分数阶微积分相关知识

分数阶微积分有各种定义，如Riemann-Liouville定义，Grünwald-Lletnikov定义，本文使用Caputo定义。［2］

定义1：α阶Caputo导数定义如下：

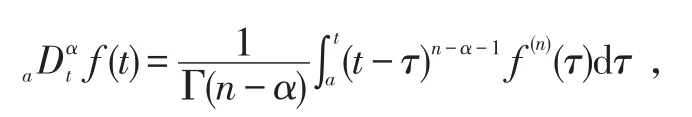
式中，n-1＜α≤n。

定义2：α阶积分计算方法如下：

式中，α＞0。

Caputo定义下导数有以下性质［2］。

性质1：线性性

性质2：零初值情况下导数复合性质

引理1：［15］对于异元线性分数阶方程组描述的系统

式中：x=（x1，x2，…，xn）∈ℝn；αi是有理数且0＜αi≤1，i=1，2，…，n。

假设M是α1，α2，…，αn分母的最小公倍数，并定义

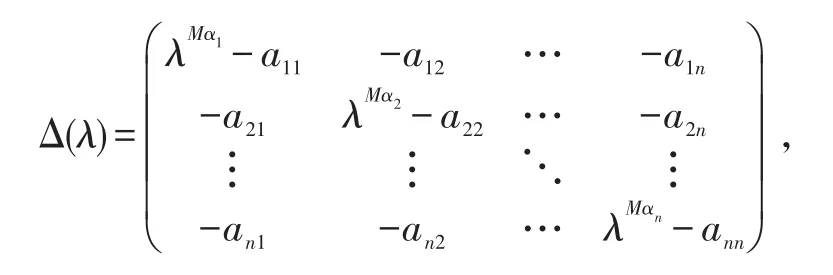
则系统零解是Lyapunov意义下全局渐近稳定的充要条件是det（Δ（λ）=0的所有的根λ满足。

引理2：［15］系统

a1x+a2D1-αx+…+anDn-1-αx+Dn-αx=0，-1＜α≤1，在Lyapunov意义下全局渐近稳定的充要条件是，分数次幂特征多项式

引理3：［22］函数x（t）∈ℝ在定义域上是连续可微的。那么对∀t≥t0，有，其中0＜α≤1。

2　整数阶系统的分数阶滑模控制

对单输入动力学系统［23］

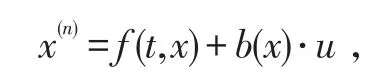
式中，x，u∈ℝ是系统的输出和控制输入。

通常，f（x）、b（x）≠0不是精确已知的，但是它们能够被已知连续函数F1（x）、F2（x）界定。

现在的控制问题是：在 f（x）、b（x）具有建模不精确性的情况下，设控制律使得状态x，跟踪特定的时变状态xd。

假设初始时刻t0=0，且初始状态满足。

令e=x-xd为跟踪误差。

2.1滑模面的设计

设计滑模面

式中，-1＜α≤1参数a1，a2，…，an∈ℝ，且满足Hurwitz条件，即满足引理2中的渐近稳定条件。

那么，方程s=0是渐近稳定的，并且s的界可以转化为跟踪误差e的界。

特别地，当n=1时。系统滑模面化简为s=a1e+D1-αe，由s=0得到D1-αe=-a1e，当a1＞0时，零解渐近稳定。

如果s有界，不妨设|s|≤C，对微分方程两边做Laplace变换，

并且注意到e（0）=0，化简得到

两边做Laplace逆变换，

其中，*是卷积符号，因此，

由Mittag-Leffler函数和函数（t-τ）α-1的性质知：

式中，B（1-α，α）是Beta函数，在α给定的情况下是常数，即e是有界的。

当n＞1时，可以通过递推的方法得到，对于满足引理2条件参数族a1，a2，…，an，当s有界时e有界。

2.2趋近律

由于e（0）=e′（0）=…=e（n-1）（0）=0，于是，

式中，j=1，…，n。

由性质2，得到DαDj-αe=Dje=e（j），于是，

设计控制量u使得：

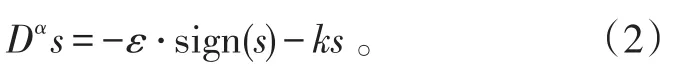
式（2）中：ε≥0；sign（s）是符号函数。

把式（2）代入式（1）得到：

当0＜α＜1时，由引理3知：

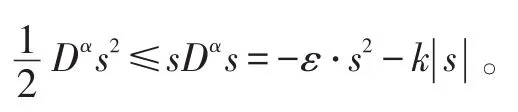
所以，在该控制律下，系统是全局渐近稳定的。

当 f精确已知时，上述控制量u的设计满足要求。

当 f不精确，或者存在随机扰动时，有2种处理方法。

方法1：在模型建立中，加入随机干扰项d（x），假设其满足|d|≤k0，系统的控制量可以设计为

此时可以得到Dαs≤-ε·sign（s）-ks，仍然满足稳定性要求。

方法2：利用 f（x）的界定函数F（x）。设此时 f（x）的估计函数为），满足。

构造控制量：

代入到Dαs中得到：

仍然满足稳定性要求。

2.3倒立摆系统控制的仿真研究

为验证本文方法的有效性，以倒立摆系统［9］作为仿真模型进行研究。

一级倒立摆的非线性方程为

x为倒立摆与垂直轴之间的夹角，m为摆的质量，2l为摆的长度，a=1/（m+M），M为小车的质量，g为重力加速度，u为控制量，此处为施加给小车的力。

取m=2kg，M=8kg，l=0.5 m，g=9.8 m/s2，初始角度 x（0）=65°，x′（0）=0，摆的期望轨迹为xd=sint。

假设系统存在随机扰动d=0.2sin（3t），本系统为二阶系统，选取滑模面

控制量

选取 α=0.75，a1=1，a2=5，ε=10，k=200，k0=0.2。

仿真结果如图1～3所示。

仿真结果显示，本文方法能够有效地完成使实际角度跟随期望角度目标，由于有随机扰动的存在，实际角度总是会产生震荡。

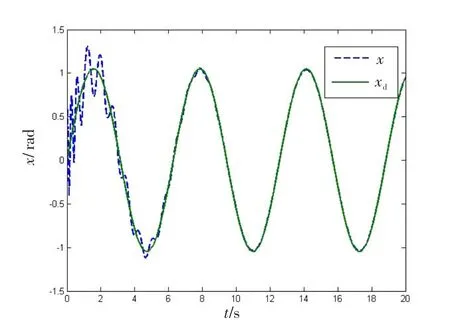
图1　实际角度x与期望角度xd时域图Fig.1 Practical anglexand expected anglexd

图2　角度误差e时域图Fig.2 Time-domain plot of errore

图3　滑模量s时域图Fig.3 Time-domain plot of the sliding modes

2.4滑模控制的最优控制阶次

本文方法中引入了滑膜控制参数α（分数阶次），仿真发现，固定其他参数的情况下，不同α的控制效果是不同的。

为了更加精确的描述控制效果，引入二次型控制性能指标：

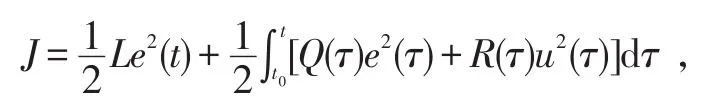
式中，L≥0，对任意t∈ℝ+，有Q（t）＞0，R（t）＞0。

二次型性能指标中：

综上，二次型控制性能指标是系统控制过程中末端状态、动态误差和能量消耗的度量，目标就是选取α使得指标J最小。

对于上文中的倒立摆系统，α与指标J变化关系如图4所示。

控制指标最优时α=0.802，此时系统各状态变化如图5～7所示。

图4　α与指标J变化关系Fig.4 Change relation ofαand indexJ

图5　实际角度x与期望角度xd时域图Fig.5 Practical anglexand expected anglexd

图6　角度误差e时域图Fig.6 Time-domain plot of errore

图7　滑模量s时域图Fig.7 Time-domain plot of the sliding modes

3　分数阶系统的分数阶滑模控制

对分数阶系统Dn+px=f（t，x），加入控制量u得到Dn+px=f（x）+b（x）·u，其中n∈ℤ+，0≤p＜1。

3.1滑模面与趋近律设计

设计滑模面

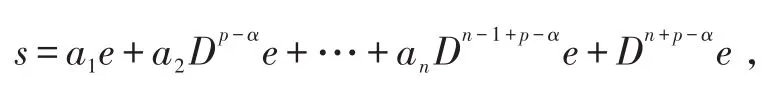
式中：-1＜α≤1；参数a1，a2，…，an∈ℝ，且满足Hurwitz条件，即满足引理2中的渐近稳定条件。

类似整数阶系统分析可以得到：

设计控制量u使得

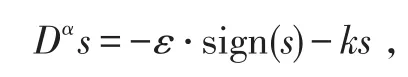
于是，

由引理3可知：

所以，在该控制律下，系统是全局渐近稳定的。特别地，n=0时，系统方程为：

对应滑模面：

控制量为

3.2分数阶Chen系统的控制仿真

本文对分数阶Chen系统的控制进行仿真研究。观察分数阶Chen系统：

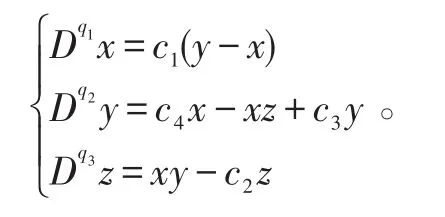
分数阶Chen系统一般是电路系统，所以可以对y进行控制，但由于观测误差的存在，这种控制不能完全使得y=0。

同时，当y=0时，系统简化为：

当c1，c2＞0时，x、z是Mittag-Leffler渐进稳定的。因此，对y加入控制：

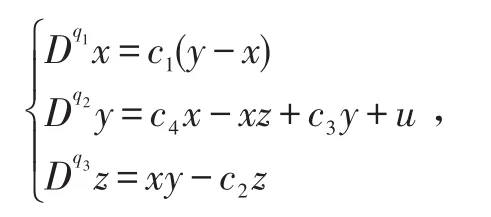
式中，

取参数（c1，c2，c3，c4）=（35，3，28，-7），阶次（q1，q2，q3）=（0.9，0.92，0.93），初始值（x0，y0，z0）=（-9，-5，14），在10 s内混沌系统仿真图像如图8～9所示。y、z的相图几乎是重合的，在下文的仿真中，只给出x、z的相图。

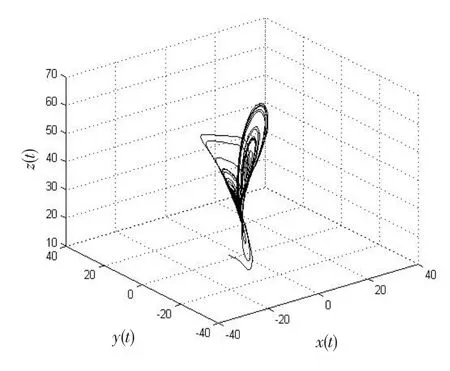
图8　（x，y，z）变化图像Fig.8 Plot of（x，y，z）

图9　x、z的时域图Fig.9 Time-domain plot ofxandz

取控制参数a=1、ε=0.1、k=0.1、α=-0.3。仿真图像如图10～12所示。

图10　控制后（x，y，z）变化图像（α=-0.3）Fig.10 Change image of control（x，y，z）（α=-0.3）

图11　控制后x、z的时域图（α=-0.3）Fig.11 Time-domain control ofxandz（α=-0.3）

取控制参数a=1，ε=0.1，k=0.1，α=0.2。仿真图像如图13～15所示。

图14　控制后x、z的时域图（α=0.2）Fig.14 Time-domain control ofxandz（α=0.2）

图15　滑模量s的时域图（α=0.2）Fig.15 Time-domain plot of the sliding modes（α=0.2）

以上2个仿真虽然只有滑模控制阶次不同，但控制效果差别很大。阶次α=-0.3时，x、y、z、s都有振动，但是总体收敛速度很快，1s内到达稳定。阶次α=0.2时，x、y、z、s不存在振动，单调趋于0，但是总体收敛速度较慢，10 s以后才能到达稳定。下面专门讨论控制阶次对控制效果的影响。

3.3滑模控制最优阶次

取a=0.012，ε=0.1，k=0.1。用前文控制指标J，仿真得J随滑模控制阶次α变化图像，见图16。在α∈（-1，1）内，控制效果在（-0.9，-0.2）内较好。此时滑模面方程含有积分项和微分项，比单纯含有微分项控制效果要好。仿真得到最优滑模控制阶次a=-0.805。此时，各状态量随时间变化见图17～20。

图16　控制指标J随滑模控制阶次α变化图像Fig.16 Change image of control orderαand indexJ

图17　最优控制下（x，y）相图Fig.17 Phase diagram of optimum control（x，y）

图18　最优控制下（y，z）相图Fig.18 Phase diagram of optimum control（y，z）

图19　最优控制下x、z时域图Fig.19 Time-domain plot of optimum controlxandz

图20　最优控制下滑模量s时域图Fig.20 Time-domain plot of the optimum control sliding modes

4　结论

本文对非线性整数阶或分数阶系统提出了统一的分数阶滑模控制方法，相对于传统的整数阶滑模控制和常用的同元分数阶滑模控制，增加了滑膜控制阶次α，多了一个控制参数，使控制器设计的灵活度大大增加。通过仿真分析，本文提出的滑模控制设计方法，对整数阶系统的最优控制滑模控制阶次为分数阶，对分数阶系统的最优滑模控制阶次α≠p，说明了本文方法的有效性。对于整数阶系统控制，分数阶的微分积分由于需要之前所有时刻的状态进行计算，比整数阶微分积分运算计算量要大，而对于分数阶系统控制而言，非同元的控制方法在计算过程中不能消去对应的分数阶微积分项，则会增加运算量。是追求要更好的控制效果，还是要更快的运算速度，需要视情而定。最后，从传统滑模控制器发展变化出的模糊滑模控制，自适应滑模控制，变结构控制等等，都可以与分数阶相结合。

［1］DIETHELM K.The analysis of fractional differential equations：an application oriented exposition using differential operators of Caputo type［M］.Berlin：Springer，2010：1-25.

［2］PODLUBNY I.Fractional differential equations：an introduction to fractional derivatives，fractional differential equations，to methods of their solution and some of their applications［M］.San Diego：Academic Press，1999：1-34.

［3］VLADIMIR V UCHAIKIN.Fractional derivatives for physicists and engineers：volume I background and theory ［M］.Beijing：Higher Education Press，2013：42-65.

［4］XUE DINGYU，CHEN YANGQUAN.A comparative introduction of four fractional order controllers［C］//Proceedings of the 4thWorld Congress，Intelligent Control andAutomation.2002.DOI：10.1109/WCICA.2002. 1020131.

［5］薛定宇，赵春娜.分数阶系统的分数阶PID控制器设计［J］.控制理论与应用，2007，24（5）：771-776. XUE DINGYU，ZHAO CHUNNA.Fractional order PID controller design for fractional order system［J］.Control Theory and Applications，2007，24（5）：771-776.（in Chinese）

［6］汪纪峰.分数阶系统性能分析［M］.北京：电子工业出版社，2011：1-33. WANG JIFENG.Control performance analysis for fractional order systems［M］.Beijing：Publishing House of Electronics Industry，2011：1-33.（in Chinese）

［7］PODLUBNY I.Fractional order systems and PIλDμcontrollers［J］.IEEE Transactions on Automatic Control，1999，44（1）：208-214.

［8］孙长银，穆朝旭，张瑞民.高超声速飞行器终端滑模控制技术［M］.北京：科学出版社，2014：1-40. SUN CHANGYIN，MU ZHAOXU，ZHANG RUIMIN. Hypersonic vehicle terminal sliding mode control technology［M］.Beijing：Science Press，2014：1-40.（in Chinese）

［9］张昌凡，何静.滑模变结构的智能控制理论与应用研究［M］.北京：科学出版社，2005：1-53. ZHANG CHANGFAN，HE JING.Sliding mode variable structure of the intelligent control theory and application research［M］.Beijing：Science Press，2005：1-53.（in Chinese）

［10］AHMED E，EI-SAYED A M A，EI-SAKA HALA A A. On some routh-hurwitz conditions for fractional order differential equations and their applications in Lorenz，RӦssler，Chna and Chen Systems［J］.Physics Letters A，2006，358：1-4.

［11］AGHABABA M P.A novel terminal sliding mode controller for a class of non-autonomos fractional-order systems ［J］.Nonlinear Dynamics，2013，73：679-688.

［12］LIU JINKUN，SUN FUCHUN.Anovel dynamic terminal sliding mode control of uncertain nonlinear systems［J］. Control Theory andApplications，2007，5（2）：189-193.

［13］ZHANG BITAO，PI YOUGUO.Fractional order fuzzy sliding mode control for permanent magnet synchronous motor servo drive［J］.Control and Decision，2012，27（12）：1776-1780，1786.

［14］SHI BAO，YUAN JIAN，DONG CHAO.On fractional model reference adaptive control［J］.The Scientific World Journal，2014：1-8.DOI：10.1155/2014/521625.

［15］YUAN JIAN，SHI BAO，JI WENQIANG.Adaptive sliding mode control of a novel class of fractional chaoic systems［J］.Advances in Mathematical Physics，2013：1-13. DOI：10.1155/2013/576709.

［16］邓立为.分数阶滑膜控制理论及其应用［D］.哈尔滨：哈尔滨工业大学，2014：1-50. DENG LIWEI.Control theory and its applications of fractional order sliding mode［D］.Harbin：Harbin Engineering University，2014：1-50.（in Chinese）

［17］XU H，MIRMIRANI M D，LOANOU PA.Adaptive sliding mode control design for a hypersonic flight vehicle ［J］.Guidance，Control，and Dynamics，2004，27（5）：829-838.

［18］DELAVARI H，GHADERI R，RANJBAR A，et al.Fuzzy fractional order sliding mode controller for nonlinear systems［J］.Communications in Nonlinear Science and Numerical Simulation，2010，15（4）：963-978.

［19］EFE M Ӧ.A sufficient condition for checking the attrativeness of a sliding manifold in fractional order sliding mode control［J］.Asian Journal of Control，2012，14（4）：1118-1122.

［20］EFE M Ӧ.Integral sliding mode control of a quadrotor with fractional order reaching dynamics［J］.Transactions of the Institute of Measurement and Control，2011，33（8）：985-1003.

［21］CRUZ VARGAS-DE-LEÓN.Volterra-type Lyapunov functions for fractional-order epidemic systems［J］.Communications in Nonlinear Science Numerical Simulation，2015，24（1-3）：75-85.

［22］N AGUILA-CAMACHO，et al.Lyapunov functions for fractional order systems［J］.Communications in Nonlinear Science Numerical Simulation，2014，19（9）：2951-2957.

［23］李惠峰.高超声速飞行器制导与控制技术［M］.北京：中国宇航出版社，2012：435-441. LI HUIFENG.Guidance and control technology for hypersonic vehicle［M］.Beijing：China Astronautic Publishing House，2012：435-441.（in Chinese）

Analysis and Design of Fractional Sliding Mode Control for Nonlinear Systems

YU Haotian，SHI Bao
（Department of Basic Sciences，NAAU，Yantai Shandong 264001，China）

In this paper，a general fractional sliding control strategy was presented for both integer order and fractional order nonlinear systems.Firstly，for inter order systems，the fractional sliding mode surfaces were desiged，whose boundedness and stability were discussed.As an numerical example，an inverted pendulum system was effectively controlled.Secondly，the introduction of control index was introduced to seek the relationship between control orderαand control effect，and it was found when optimal control index was reached，α∉ℤ.Finally，the method was applied in fractional order systems.The effective control of a fractional Chen system showed the effectiveness of the proposed method.And it showed that when optimal control index was reached，the control order didn’t equal to system’s order.

nonlinear control systems；fractional order systems；fractional sliding mode control；inverted pendulum；fractional Chen system

TP391

A

1673-1522（2016）04-0407-08

10.7682/j.issn.1673-1522.2016.04.002

2016-03-06；

2016-04-13

山东省自然科学基金资助项目（ZR2014AM006）

于昊天（1988-），男，硕士生；时宝（1962-），男，教授，博士，博导。