一类具有分布时滞和离散时滞中立型积分微分方程周期解

周　刚，刘孝磊，赵文飞

（海军航空工程学院基础部，山东烟台264001）

一类具有分布时滞和离散时滞中立型积分微分方程周期解

周刚，刘孝磊，赵文飞

（海军航空工程学院基础部，山东烟台264001）

考虑了具有分布和离散时滞的方程周期解的存在性问题。文章通过利用线性系统的指数二分性和Krasnoselskii不动点定理得到了上述方程周期解存在唯一的充分条件，结论推广和改进了已有文献的结果，并通过一个例子说明该结果的优越性。

分布时滞；离散时滞；周期解；指数二分性；不动点定理

无穷时滞泛函微分方程周期解的存在性问题一直受到人们的广泛关注。

通过构造适当的Lyapunov泛函，可以得到标量Volterra型积分微分方程

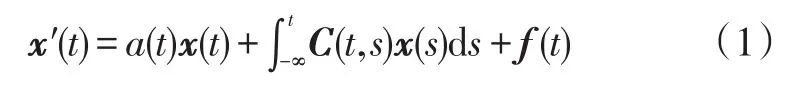
周期解存在性的充分条件。彭世国等［1］运用不动点定理在较弱的条件下，得到了方程（1）周期解存在唯一性。王全义［2］讨论了中立型标量积分微分方程：

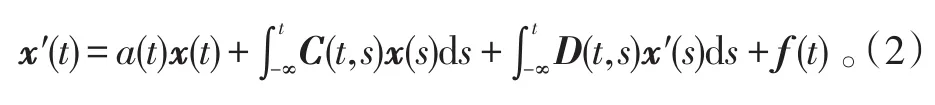
利用Leray-Schauder和压缩映像原理讨论了方程（2）的周期解的存在性，唯一性和稳定性问题。文献［3-8］研究了无穷时滞Volterra型积分微分方程周期解的存在性，得到了不少好的结果。杨喜陶［9］利用Schauder不动点定理研究了方程：

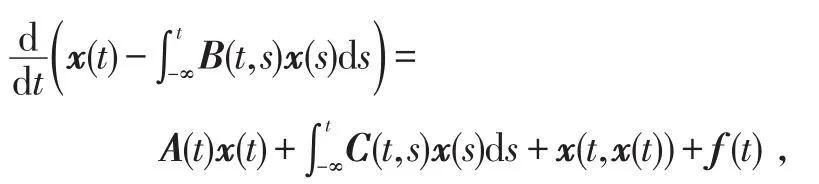
得到其周期解存在的条件。陈凤德等［10］研究了方程：

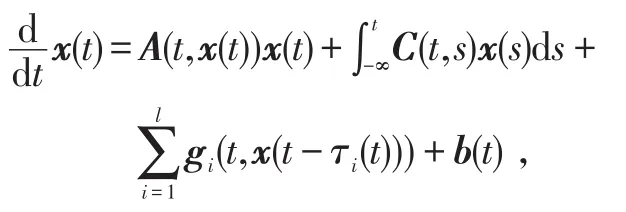
利用指数二分性和不动点定理，在不同的条件下，得到了不少有关周期解存在性的结果。

受文献［8-12］的启发，考虑如下更加广泛的具有分布时滞和离散时滞中立型积分微分方程：

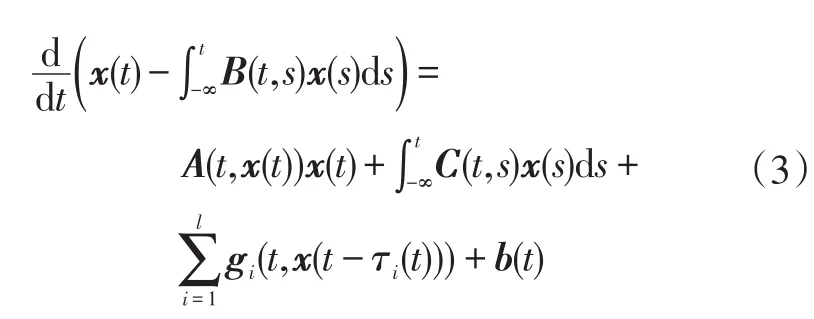
的周期解存在性问题。

为方便起见，先做如下假设。

A1：设存在正的连续可微的T-周期函数di（t），i=1，2，…，n和连续的T-周期函数α1（t）满足

A4：存在非负连续的T-周期函数 ci（t），使得对于t∈ℝ一致成立。

A5：存在常数，使得对于任给的t∈ℝ，有，其中，α1（t）、ci（t）分别由A1和A4决定。

1　几个引理

考虑周期系统

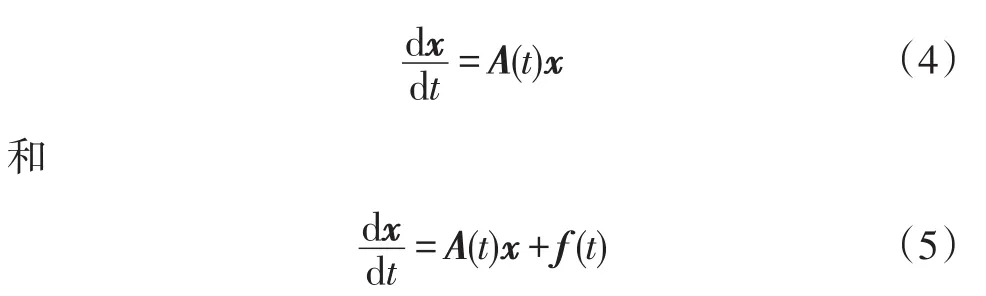
假设B：设存在正的连续可微的T-周期函数di（t），i=1，2，…，n和连续的T-周期函数α2（t）满足：

引理1［12］：设X（t）是方程（4）的基本解矩阵，若A（t）满足假设B和A2，则有且方程（5）存在唯一的T-周期解

引理2［11］：设λ（t）是连续的T-周期函数，则对任意的t∈ℝ有

引理3［2］：设C（t，s）是n×n连续函数矩阵且满足条件A3，f（t）是ℝ上的n维连续的T-周期函数，则也是连续的T-周期函数。

引理 4［11］：若 T-周期函数α2（t）满足，则：

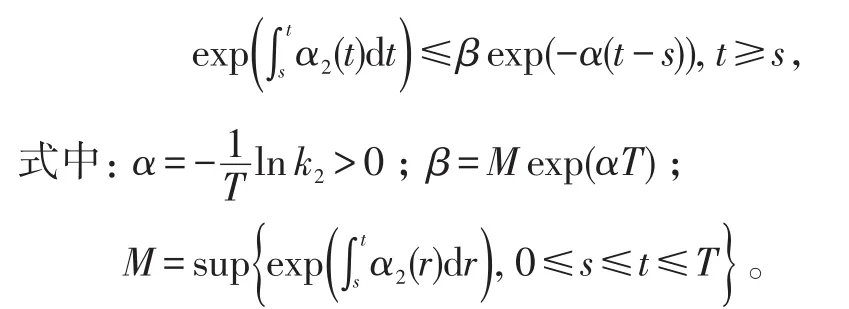
引理5：［12］（Krasnoselskii不动点定理）设S是实Banach空间X中有界凸闭集，F，I:S→X，满足：

1）F:S→S全连续；

2）I:S→S是压缩映像；

3）对任意的u，v∈S，有Fu+Iv∈S，则F+I在S中至少存在一个不动点。

2　主要结果

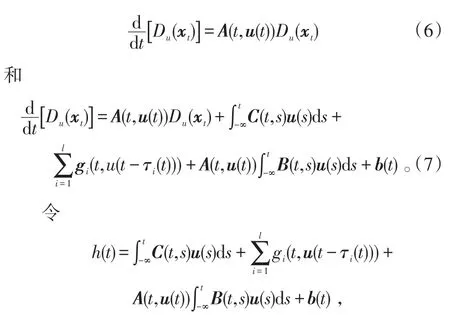
由定理条件及引理2、4易知h（t）是连续的T-周期函数。

设Xu（t）是方程（6）的基本解矩阵，故根据定理的条件及引理1知方程（7）有唯一的T-周期解：

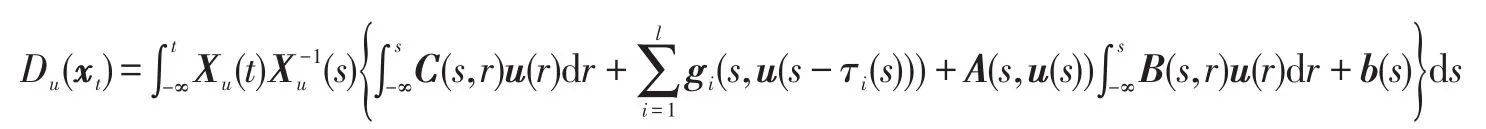
今在CT中定义算子F、I和G如下：

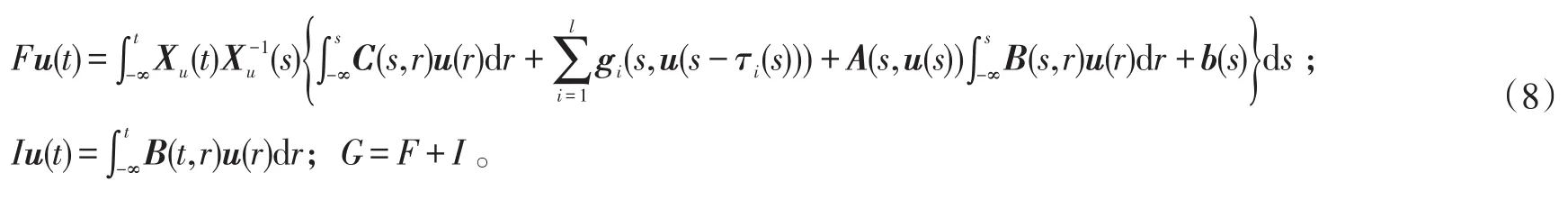
易知F、I和G是CT上的自映射。

（Ⅰ）F:DN→DN全连续；

（Ⅱ）I:DN→DN是压缩映像；

（Ⅲ）对任意的u，v∈DN，有Fu+Iv∈DN。

首先，证明（Ⅰ）。

1）证明存在自然数N，使得F:DN→DN。

以及充分大的自然数Nl+1，使得。现在取M＞max｛N1，N2，…，Nl，Nl+1｝，则当N＞M时，

同时成立。

于是，由定理条件及引理1和式（8）、（9）可得当N＞M时，有：

因此，当n充分大时，‖Fu（t）‖＜n，即存在充分大的自然数N，使得F:DN→DN。

2）证明FDN是CT中的紧子集。事实上，因为FDN⊆DN，所以｛Fu（t）|u∈DN｝是一致有界的。又

从而对任意的u∈DN有：

故｛Fu（t）|u∈DN｝是等度连续的，由Ascoli-Arezela定理可知FDN是CT中的紧子集。

3）证明F在DN上连续。对任意的u1，u2∈DN，因为gi（t，x）在［0，T］×RN上是一致连续的，且关于t是T-周期的，故gi（t，x）在ℝ×RN上是一致连续的，从而对于任意的ε＞0，存在δi=δi（ε）＞0（i=1，2，…，l），使得当‖u1-u2‖≤δi时，有

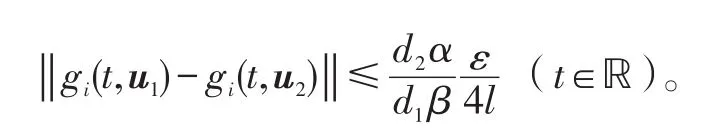
同样，也存在δl+1＞0，使得当时，有

另外，有：

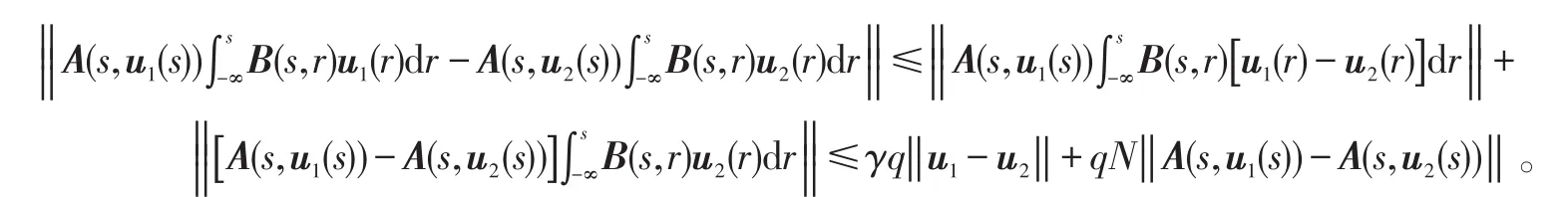
现取

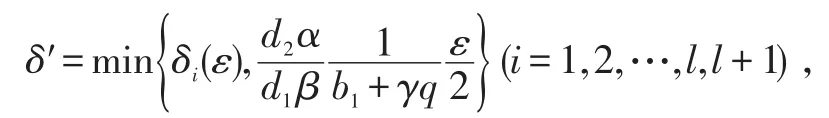
于是由定理条件可知对于任意的u1，u2∈DN，t∈ℝ，只要，就有

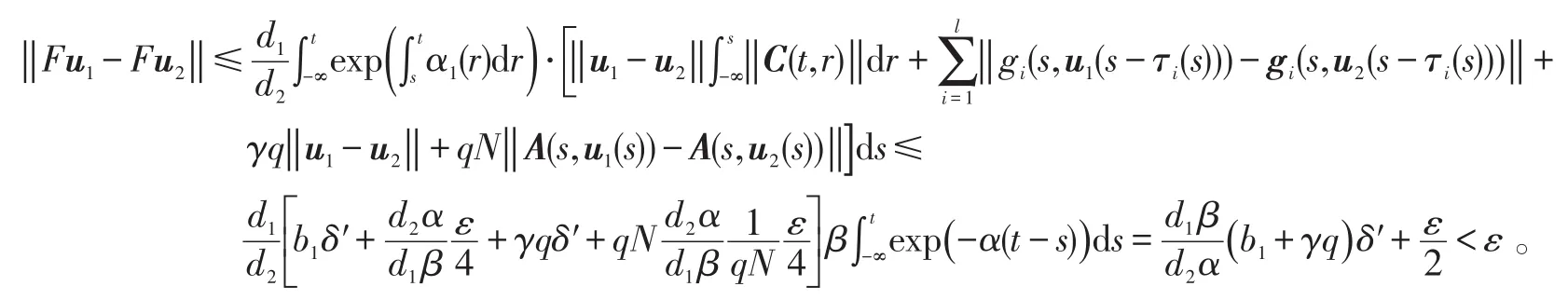
综合上面的证明可知F:DN→DN是全连续算子。

其次，证明（Ⅱ）。

因为对于任意u∈DN，有

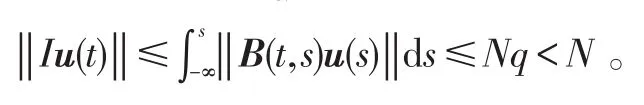
所以，I在DN上是压缩映像的。

最后，证明（Ⅲ）。

由前面的证明可知对于任意的u，v∈DN，有‖Fu‖≤N（1-q）和‖Iv‖≤Nq，从而可得

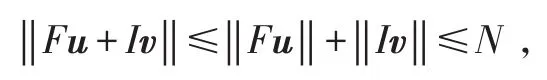
即，Fu+Iv∈DN。

故根据引理5知F+I在DN上至少有一个不动点u0（t），从而有

就是方程（7）在u（t）=u0（t）时的周期解，这也说明了方程（3）至少存在一个连续的T-周期解。

注1：与文献［1］的结果相比，其条件（1）是本文中di（t）≡1，B（t，s）=Q（s-t）的特殊情况；其条件（2）中要求存在，本文中不需要这个条件。实际上，一般情况下这个条件不易满足，例如简单情形A（t，x）=x就不满足。

注2：文献［10］中的定理2.2是本文中B（t，s）≡0时的特殊情况。

3　应用举例

考虑下列二维具有无穷时滞中立型泛函积分微分方程：

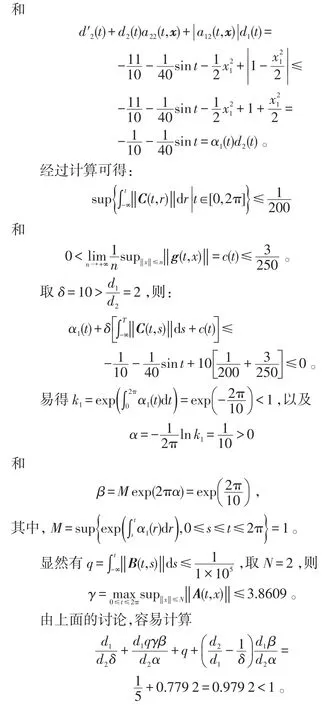
从而定理1的条件满足，因而可知方程（10）至少有一个2π-周期解。

显然，方程（10）的2π-周期解的存在性用已有文献所提供的方法是无法判断的。

［1］彭世国，朱思铭.具有无穷时滞泛函微分方程的周期解［J］.数学年刊，2002，23A（3）：371-380. PENG SHIGUO，ZHU SIMING.Periodic solutions of functional differential equations with infinite delay［J］. Chinese Annals Of Mathematics，2002，23A（3）：371-380.（in Chinese）

［2］王全义.具有无限时滞的积分微分方程解的存在性唯一性及稳定性［J］.应用数学学报，1998，21（2）：312-318. WANG QUANYI.The existence，uniqueness and stability of solution on a integro-differential equation with infinite delay［J］.Acta Mathematicae Applicatae Sinica，1998，21（2）：312-318.（in Chinese）

［3］常啸.一类具无穷时滞中立型积分微分方程周期解［J］.大学数学，2007，23（2）：62-64. CHANG XIAO.The periodic solutions for a class of neutral integro-differential equations with infinite delays［J］. College Mathematics，2007，23（2）：62-64.（in Chinese）

［4］陈凤德.具无限时滞的非线性积分微分方程的周期解［J］.应用数学学报，2003，26（1）：141-148. CHEN FENGDE.Periodic solutions of nonlinear integrodifferential equations with infinite delay［J］.Acta Mathematicae Applicatae Sinica，2003，26（1）：141-148.（in Chinese）

［5］江娇，徐建华.具有无穷时滞中立型积分微分方程的周期解［J］.数学物理学报，2008，28A（5）：897-905. JIANG JIAO，XU JIANHUA.Periodic solutions of neutral integro-differential equations with infinite delay［J］. Acta Mathematica Scientia，2008，28A（5）：897-905.（in Chinese）

［6］罗芳琼.一类具有无穷时滞的中立型泛函微分方程的周期解［J］.柳州师专学报，2010，25（1）：120-128. LUO FANGQIONG.Periodic solution for a class of neutral type functional differential equations with infinite delays［J］.Journal of Liuzhou Teachers College，2010，25（1）：120-128.（in Chinese）

［7］张洪彦，王奇，丁敏敏.一类具有无穷时滞中立型泛函微分方程反周期解的存在性［J］.佳木斯大学学报，2012，30（1）：151-154. ZHANG HONGYAN，WANG QI，DING MINMIN.Existence of anti-periodic solution for a class of neutral functional differential equation with infinite delays［J］.Journal of Jiamusi University，2012，30（1）：151-154.（in Chinese）

［8］王晓，李志祥，张浩.具有无穷时滞中立型泛函积分微分方程周期解的存在性［J］.应用数学，2006，19（4）：804-811. WANG XIAO，LI ZHIXIANG，ZHANG HAO.The existence of periodic solution on a neutral integro-differential equation with infinite delay［J］.Mathematica Applicata，2006，19（4）：804-811.（in Chinese）

［9］YANG XITAO.Existence and exponential stability of al-most periodic solution for hopfieldneural network equations with almost periodic imput［J］.Journal of Northeasten Mathematics，2006，22（2）：199-205.

［10］陈凤德，孙德献，史金麟.一类积分微分方程周期解的存在性和唯一性［J］.数学学报，2004，47（5）：973-984. CHEN FENGDE，SUN DEXIAN，SHI JINLIN.On the existence and uniqueness of periodic solutions of a kind of integro-differential equations［J］.Acta Mathematica Sinica，2004，47（5）：973-984.（in Chinese）

［11］ZHOU ZONGFU，ZENG LI，JIA BAORUI.Periodic solutions for a class of neutral functional differential equations with distributed and discrete delays［J］.Chinese Quarterly Journal of Mathematics，2012，27（4）：485-494.

［12］谢胜利.有阻尼的二阶脉冲无穷时滞泛函微分方程解的存在性［J］.数学物理学报，2015，35A（1）：97-109. XIE SHENGLI.Existence results of damped second order impulsive functional differential equations with infinite delay［J］.Acta Mathematica Scientia，2015，35A（1）：97-109.（in Chinese）

Periodic Solutions for a Class of Neutral Integro-differential Equations with Distributed and Discrete Delays

ZHOU Gang，LIUXiaolei，ZHAO Wenfei
（Department of Basic Science，NAAU，Yantai Shandong 264001，China）

Using the exponential dichotomy and Krasnoselskii’s fixed point theorem，the existence of periodic solutions for a class of integral- differential equations with distributed and discrete delayswere discussed.These results improves and extends the existing results，which was constructed by an example to illustrate the feasibility.

distributed delays；discrete delays；periodic solutions；exponential dichotomy；fixed point theorem

O175.13

A

1673-1522（2016）04-0495-06

10.7682/j.issn.1673-1522.2016.04.016

2016-05-23；

2016-06-28

山东省自然科学基金资助项目（ZR2014AM006）

周刚（1975-），男，副教授，硕士。