一种鲁棒的概率核主成分分析模型

杨　芸，李　彪，王帅磊

（海军航空工程学院a.研究生管理大队；b.基础部，山东烟台264001）

一种鲁棒的概率核主成分分析模型

杨芸a，李彪b，王帅磊a

（海军航空工程学院a.研究生管理大队；b.基础部，山东烟台264001）

大数据时代面临的数据维数越来越高，对数据降维处理越发显得重要。经典的主成分分析模型已被证明是一种有效的数据降维方法。但它在处理非线性、存在噪声和异常点的数据时存在效果较差的问题。对此，文章提出了一种鲁棒概率核主成分分析模型。该模型将核方法与基于高斯隐变量模型的极大似然框架相结合，用多元t分布作为先验分布，以同时解决主成分分析在这3个方面的弊端。提出混合鲁棒概率核主成分分析模型，使其可直接用于对混合的非线性数据进行降维和聚类分析。在不同数据集上进行的实验结果表明，与标准的混合概率核主成分分析模型相比，文中模型在数据聚类方面有更高的准确率。

主成分分析；鲁棒降维；EM算法；聚类分析；核方法；隐变量模型

随着信息技术的飞速发展，面对的数据维数越来越高。在进行数据分析时，为能有效地从高维数据集中挖掘有用的信息，线性和非线性的数据降维技术变得越来越重要，受到了计算机视觉和图像分析等领域的广泛关注［1-3］。主成分分析（Principal Component Analysis，PCA）是一种经典的数据分析方法［4］，它本身及其拓展作为有效的数据降维技术在数据降维或数据的低秩恢复、数据聚类、模式识别等方面得到了重要的应用［5-6］。

经典的PCA方法虽然在数据降维方面简洁有效，求解起来也较容易，但其存在几个方面的不足。第一，它没有考虑数据本身的分布特征，而这一点对于混合数据建模十分重要；第二，它只是一种线性的降维方法，会损失掉高位统计信息；第三，降维效果受异常点的影响很大，数据中异常点的存在可能导致不稳定的主成分，从而影响数据降维和在低维空间进行聚类的准确性。针对第一个方面的不足，一些文献将基于高斯隐变量模型的极大似然框架引入PCA中，使得可以用一种独立的方式来组合PCA模型，在高维数据的混合建模分析方面取得了较好的效果［7-9］。在对非线性数据进行建模分析方面，核方法是一种较好的将非线性数据线性化的方法。它先将数据映射到高维核空间，对非线性数据进行线性化处理，然后在核空间中对数据进行处理［10］。所以，对于第二个方面的不足，有些文献将核方法用于主成分分析，即先将数据映射到高维核空间，然后在核空间中对数据进行降维，对第二个方面的不足进行了有效的建模分析［11］。而针对第三个方面的不足，一些文献通过将PCA与新的理论相结合，比如谱图理论［6］，贝叶斯统计推断［12］等，提出了大量鲁棒性方法［13-15］，来减少异常点的影响。而文献［16］通过将核方法与基于高斯隐变量模型的极大似然框架相结合，对PCA中存在的第一个和第二个方面的不足进行了建模分析。但它以多元正态分布作为先验分布，使得模型对于异常点较为敏感，从而影响对数据降维和聚类的准确率。相比于正态分布，t分布是“肥尾”分布，也就意味着它对于异常点有更小的敏感性。且对于有些问题，并不能收集到足够多的数据，因而在这种情况下，假设样本服从正态分布是不合理的。所以，文献［17］用多元t分布代替文献［7］中的多元正态分布来作为先验分布，有效的减少了异常点的影响，加强了鲁棒性，使得模型的准确率有了较大的提高，并在手写数字的识别上取得了较好的效果。但它无法直接用于对混合的非线性数据的降维和聚类分析，限制了模型的应用范围。

本文提出一种鲁棒概率核主成分分析（Robust Probabilistic Kernel Principal Component Analyzer，RPKPCA）模型，是对经典的PCA方法的改进。一方面，使其在小样本情形下也能有较高的准确率；另一方面，减少模型对于异常点的敏感性，使其用于数据聚类和降维时的准确率得到提高。并在此基础上，构建混合鲁棒概率核主成分分析模型（Mixtures of Robust Probabilistic Kernel Principal Component Analyzers，MRPKPCA），便于模型直接用于对混合数据的降维和聚类分析，且能同时解决上文提出的经典PCA方法的一些不足之处。相比于以前提出的方法，本文所提方法的优势在于将PCA方法与基于高斯隐变量模型的极大似然框架相结合，充分考虑了样本本身的分布。并且利用多元t分布作为先验分布，减少了模型对于异常点的敏感性，提高了模型对于数据降维和聚类结果的准确率。同时，结合核方法，使得模型能直接处理混合的非线性数据，与文献［17］中所提方法相比，模型的应用范围更加广泛。

1　核空间统计因素分析模型简介

对于数据集｛y1，y2，…，yN｝，yn∈ℝD，1≤n≤N，先通过非线性映射φ:ℝD→ℝf将其映射到高维特征空间（也称核空间），其中，f＞D，甚至可以是无穷大，然后在高维特征空间中对其进行处理。而对于D维数据向量y，在其高维特征空间，可以假设它服从一个特别的因素分析模型［16］，表示为：

式（1）中：φ（y）表示数据向量y到其高维特征空间的映射函数；x～N（0，Id）为一个d维的隐空间向量；ε～N（0，ρIf）表示 f维噪声向量；W为一个D×d维的载荷矩阵；μ表示y的均值向量，且d＜＜f。

1.1一些基本定义

核函数即映射φ有多种定义方式，包括线性核函数、多项式核函数、高斯核函数（或RBF核函数）。近些年有大量的文献对其进行探讨，包括核函数选择和参数优化［10，18-19］。其中，高斯核函数在应用方面相对较广泛。所以，本文也将用高斯核函数进行探讨。其形式为：

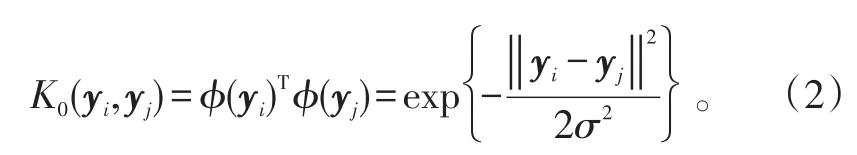
式（2）中：∀yi，yj∈ℝD；σ为控制核宽度的参数。

对于特征空间中的均值和协方差矩阵，定义为：

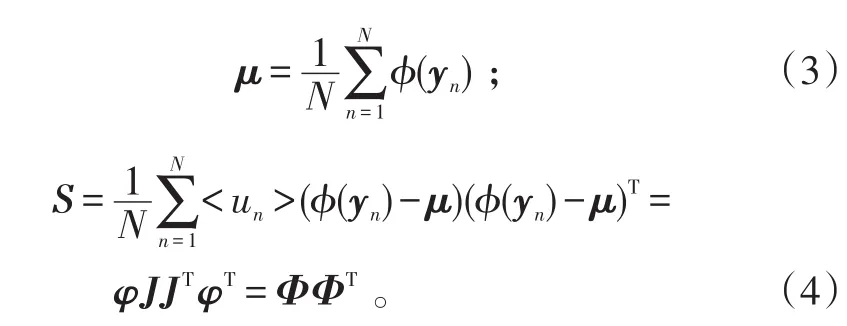
定义sN×1=N-11，1∈ℝN，表示每个元素均为1的列向量。则有

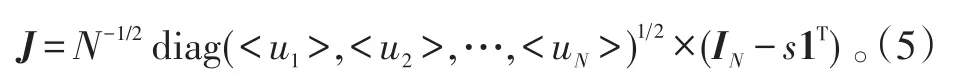
另外，定义：

S的前d个最大特征值对应的特征向量［16］

式（7）中：Λd和Vd=［v1，v2，…，vd］分别为该矩阵K的前d个最大特征值与其对应特征向量组成的矩阵，且Vd∈ℝD×d，Λd∈ℝd×d。

1.2基本模型

在式（1）所提到的核空间统计因素分析模型中，许多文献往往是通过假设样本在低维空间中服从正态分布来进行分析的。根据小样本理论，当样本数量有限且较少时，假设其服从正态分布会使得整个推断出现较大的偏差，且受异常点的影响很大，从而使模型的准确率较低。因此，为了增强标准的概率核主成分分析模型（Probabilistic Kernel Principal Component Analyzer，PKPCA）的鲁棒性，使其在样本较少时也能有较高的准确率，并减少异常点的影响。本文使用多元t分布（关于多元t分布的介绍可参见文献［20］）代替多元Gaussian分布作为先验分布，即假设样本在低维隐空间中服从多元 t分布［17］。这样，在给定μ、Σ、v的情况下，有

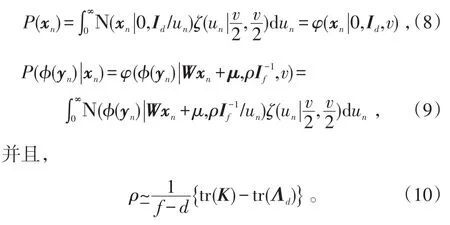
式（9）、（10）中，规模协方差是数据独立的，且对每一个φ（yn）指定不同的规模变量un。另外，每一个规模变量un的gamma先验分布由隐向量xn和观测映射向量φ（yn）所共享。因此，隐空间和高维特征空间的鲁棒性由单独的参数v决定。所以，当一个数据点在高维特征空间被认为是一个异常点时，它将不会对主子空间的鉴别有任何贡献，因而它在隐空间，即投影空间也被认为是一个异常点［17］。

1.3权重矩阵W的估计

以多元t分布作为隐变量的先验分布，在给定μ、Σ、v的情况下，有：

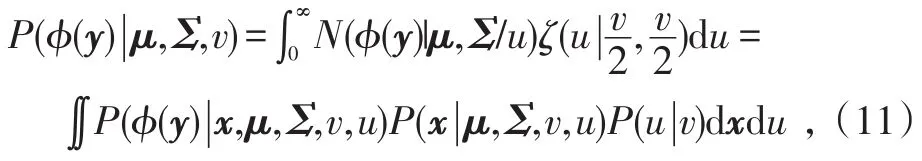
式中，μ和Σ分别表示高维特征空间中的均值和协方差矩阵，且有

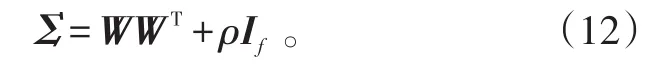
所以，可得全部数据的对数似然函数的期望为：［21］

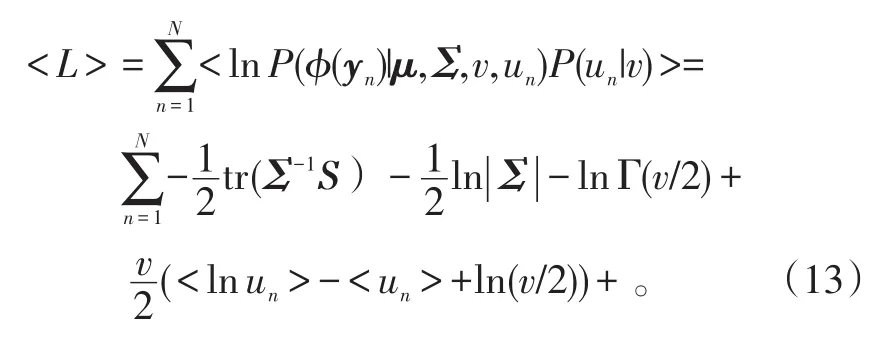
通过贝叶斯法则，得规模变量un的后验分布为：

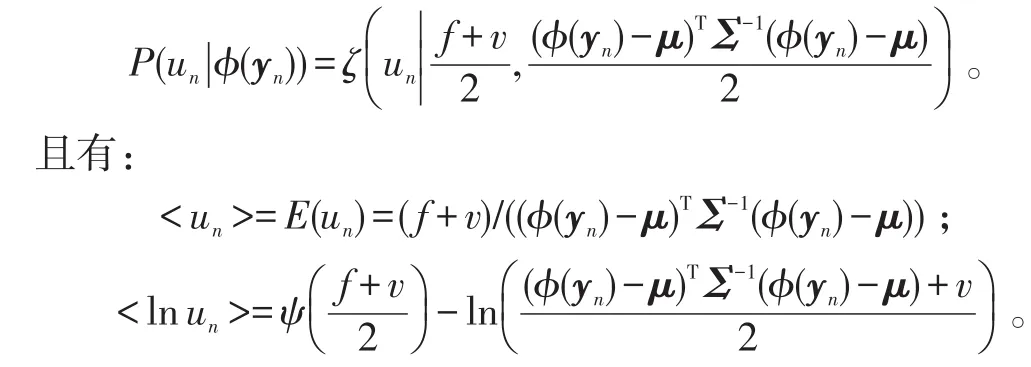
当W的列向量张成高维特征空间的主子空间时，式（13）所示的对数似然函数最大［7］。所以，可以求得

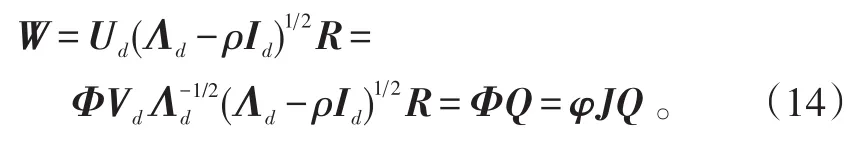
式（14）中：R为任意d×d维正交矩阵；Id表示d×d维单位矩阵；Q定义为N×d维矩阵，

从式（15）看出，W位于φ的线性子空间。故通过算法求得矩阵Q就可对数据进行降维和聚类分析［16］。

2　混合鲁棒概率核主成分分析模型

用一个RPKPCA无法对混合数据进行建模分析。现实中处理的数据分析任务，需要从高维混合数据中挖掘出某些有用信息。因此，对数据进行建模分析时，混合多个鲁棒概率主成分分析器是必要的。所以，将混合的M个鲁棒概率主成分分析模型定义为：

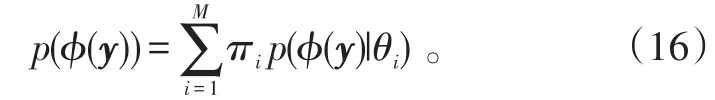
式（16）中：πi为混合比例，θi为分析器的参数，对所有的i，有θi=｛μi，Qi，ρi，vi｝。

2.1用EM算法对模型进行训练

本文选择用最大化似然函数L0来估计模型的参数｛μ，Q，ρ，v｝。但是，由于v和 f未知，无法一开始就给出准确的J矩阵的值，因而无法通过直接求取K的特征值和特征向量来给出Q矩阵，所以通过合适的算法来对其进行求解。EM算法是应用最广泛的一种求解混合概率模型参数的算法，它的基本原理为通过迭代使得模型的对数似然函数最大化［22］。因而，本文也用EM算法对模型进行求解。得到似然函数为［17］：

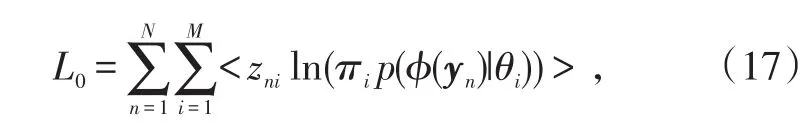
式中，zni为指示器参数，表示的是数据点n属于分析器i的几率，且，定义

具体过程为，首先（E步），固定各参数给出隐变量的后验分布，并计算出对应的期望值；然后（M步），对参数进行更新，直到参数收敛。

E步：计算所示量。

由于 f未知，且可能为无限大，所以无法用式（20）、（21）对相应值进行计算。但是，通过在本文第3部分所示3个数据集上进行测试，发现 f=9时，在3个数据集上均得到了较好的结果。所以，文中在利用式（20）、（21）进行计算时，将 f设置为固定值9。

M步：对参数进行更新，具体公式为：

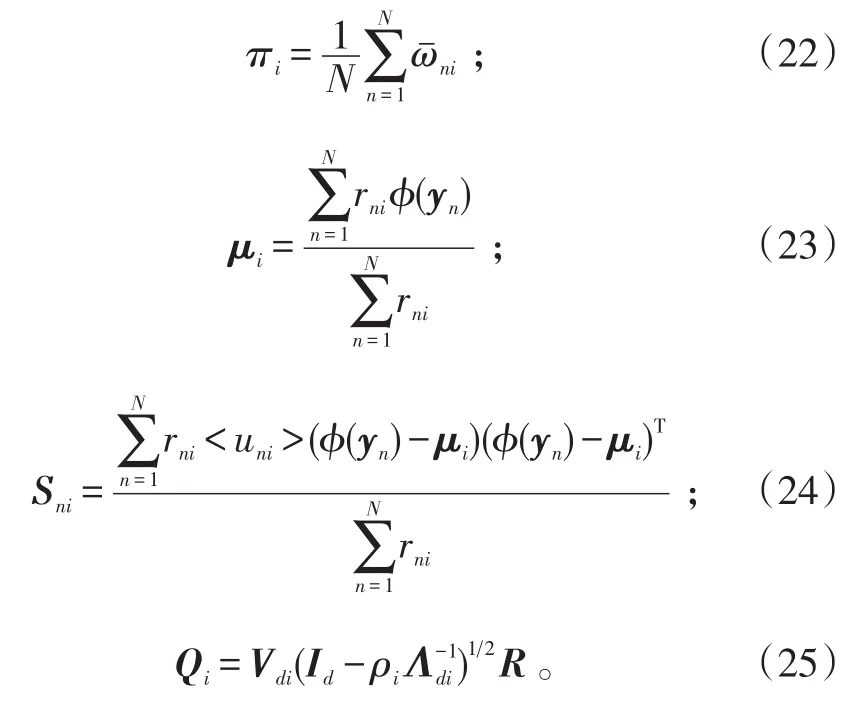
式（22）～（25）中：Λdi=diag（λ1i，λ2i，…，λdi），其中，（λ1i，λ2i，…，λdi）分别表示Sni的前d个最大特征值；Vdi为Sni的前d个最大特征值对应的特征向量。

通过对数似然函数L0可求得于ρi与 f成反比，而 f值本身较大，且可能是无限大，无法根据公式估计出。另外，求得的ρi值的估计式十分复杂，用迭代计算 ρi值并不合适。而 ρi值与 f成反比，其本身是很小的，因而在迭代计算的时候，可以通过人为选择，设定ρi为一个固定的很小的值。而在ρi固定的情况下，选择式（25）迭代计算Qi值是可行的。因此，对所有的类别i，将 ρi设成固定的比较小的一个常数，即ρi≡ρ=c。并且，如果能先行计算出K和K0值，则每一次迭代计算的计算复杂度为O（dN2）。而每个数据点的贡献就由来衡量，它是和的乘积。当数据点n远离第i类的中心μi时，的取值会很小，从而确保了算法对于异常点的鲁棒性。

类似于式（4），可以将Sni写成：

因此，可以通过求矩阵Ki=JiTK0Ji的特征值和特征向量，从而得到Λdi和Vdi。

2.2各分析器参数vi的确定

由于各分析器的“鲁棒性”由唯一的参数vi决定，所以对于参数vi的设置十分重要。文献［23］中提出通过求解如下非线性函数来得到vi的值：

在具体计算中，可以通过一个线性搜索算法［24］来求取式（28）的最优数值解。但为了减少计算复杂度，在本文中，采用文献［22］中提到的数值近似方法，

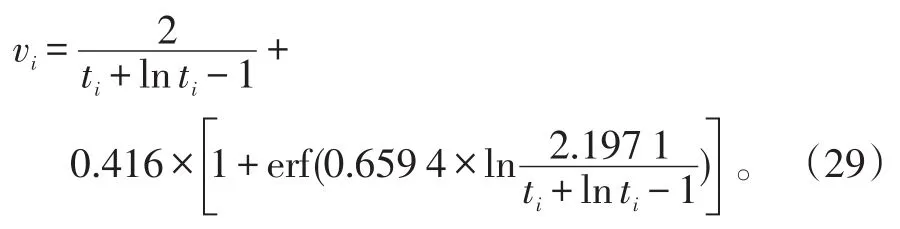
3　实验测试与结果分析

本文的实验测试环境为MATLAB R2014a，通过在人工数据集和实际数据集上进行仿真分析，来验证模型的有效性。

3.1低维人工数据集聚类分析

为了使得测试结果更直观且进行有效的比较，构造重构误差百分比η来比较模型的有效性，其具体形式为：

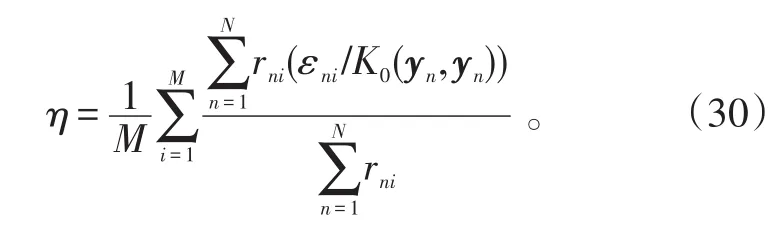
根据文献［16］中所示，最好的φ（yn）的拟合值为：

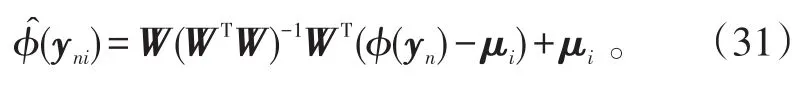
进一步可以得到：

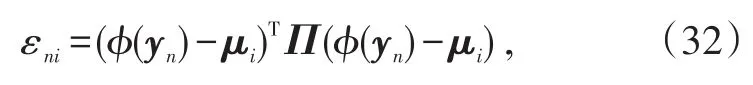
式中，Π=If-W（WTW）-1WT。

从式（32）可以看出，当聚类效果不好时，会存在一些聚类不准确的点，使得εni的值较大。从而使得rni×εni较大，进而影响重构误差百分比的值，使其较大。

为了验证模型在低维数据集上的有效性，选择由如下函数产生的人工数据集

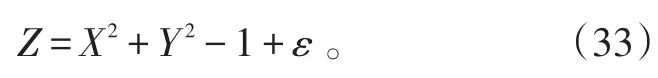
进行仿真分析时，使用式（33）所示函数，共产生了441个数据点，分布在一个三维的双曲面上。并且在双曲面上加入了40个异常点，分布在双曲面的4个方向上，见图1。

图1是根据标准的混合概率核主成分模型MPKPCA（Mixtures of Probabilistic Kernel Principal Component Analyzers）得到的结果，各参数取值分别为d=5，σ=0.90，ρ=0.005，而图2是根据MRPKPCA模型得到的结果，各参数取值为d=5，σ=0.85，ρ=0.001。

图1　通过MPKPCA模型得到的投影图Fig.1 Projection by model of MPKPCA

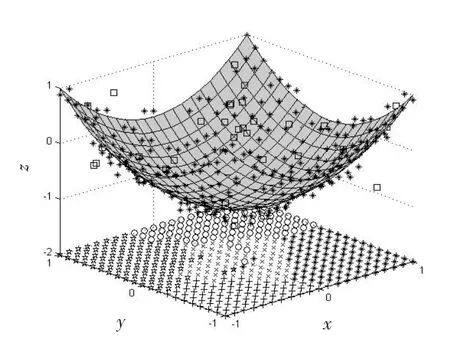
图2　通过MRPKPCA模型得到的投影图Fig.2 Projection by model of MRPKPCA

通过图1与图2进行对比，可以看出，在使用MRPKPCA模型对数据进行聚类时，得到的各个类别所包含的数据点的个数比较均匀。且位于图中间的类别所包含的数据点的数量不会很多、很分散，这就有效的保证了数据的集中度与分类的准确性，使得重构误差平均百分比η相比而言较小。图1中对应的η值为1.25%，而图2中对应的η值为0.38%。

为了更直观的进行比较，表1给出了MRPKPCA模型和MPKPCA模型在不同最终降维数d下的平均重构误差百分比和最小重构误差百分比（其他参数均为在调试后较优的值）。

由表1可看出，MRPKPCA模型相较标准的MPKPCA模型有更小的重构误差百分比。这表明MRPKPCA模型在对数据聚类时，每一类的数据点更加均匀且集中，受异常点的影响较小，从而使分类结果的准确性得到较大的提高。所以，根据表1的对比分析，可以知道，MRPKPCA模型对异常点有着较好的鲁棒性，且在对低维数据进行聚类时有着较高的准确率。

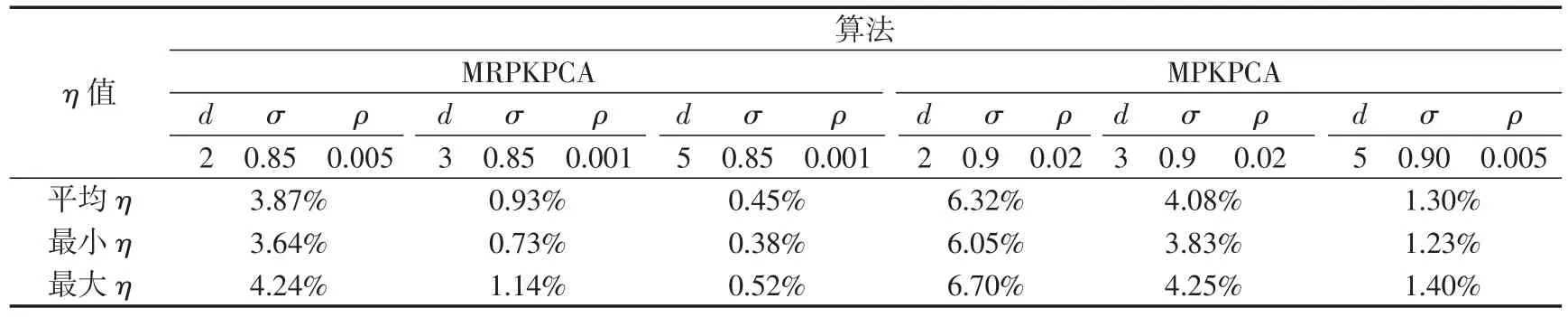
表1　不同最终降维数下的η值Tab.1 Values ofηunder different final number of dimensionality reduction

3.2高维数据聚类分析

数据来源于经典的UCI数据库中的“Image Segmentation”数据集［25］。该数据集包含用于训练的“segmentation_data”和用于测试的“segmentation_test”的数据。“segmentation_data”中共210条数据，每条数据有19个维度，为7种不同户外景物在30种不同情境下的照片分割信息。而“segmentation_test”中共2 100条数据，为与“segmentation_data”中对应的7种景物在300种不同情境下的照片分割信息。

为了验证模型对于高维数据聚类的有效性，从“segmentation_test”中选取前3种景物的照片分割信息，共900条数据（即900×19的矩阵）来进行聚类比较分析。图3给出的是在最终降维数d=2时，MRPKPCA模型根据Q矩阵给出的降维效果图。

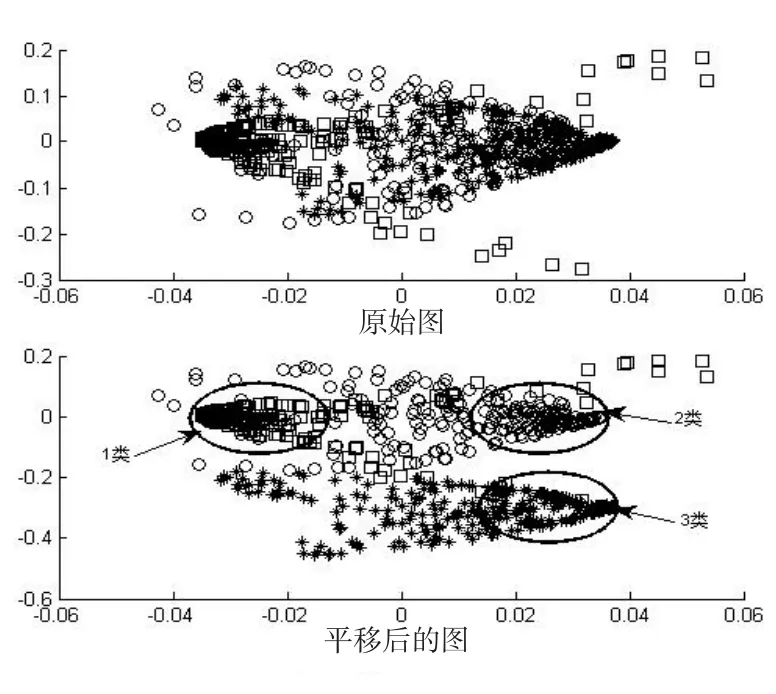
图3　通过MRPKPCA模型得到的降维效果图Fig.3 Effect picture after dimensionality reduction by MRPKPCAmodel

从图3中可以看出，MRPKPCA模型能有效的对高维数据进行降维，使得相同类型的数据在降维后能聚在一起。由于图3给出的只是单次降维后的效果图，其结果并不具有很大的说服力。因而，在表2中给出了在不同最终降维数下，不同模型的平均聚类准确率，其中KFC-M表示基于核方法的模糊C均值聚类算法。将聚类准确率定义如下，

式（34）中：t表示一次聚类中分类正确的样本数；h表示用于聚类的样本总数。

通过对表2的分析可看出，MRPKPCA模型在减少数据异常点的影响，提高聚类准确率方面，有着相当大的潜力。虽然在维数很低时，模型的平均准确率比标准的MPKPCA模型要小，但其单次准确率可能很大，明显大于标准的MPKPCA模型。且随着最终降维数的逐渐增加，MRPKPCA模型的准确率也在不断增加。当最终降维数d=5时，MRPKPCA模型的准确率已经远大于标准的MPKPCA模型和KFC-M算法。

表2　不同最终降维数下的θ值Tab.2 Values ofθunder different final number of dimensionality reduction

根据表2中的对比分析，可以知道，在对高维数据进行降维和聚类时，与标准的MPKPCA模型、KFC-M算法［26］相比，MRPKPCA模型有着较高的准确率。

3.3高维小样本数据聚类分析

为验证模型在对小样本数据进行降维和聚类时的有效性，这部分选取“2015年全国研究生建模竞赛B题第3小题（c）问”中提供的数据进行实验测试［27］。数据的维度为2 016×20，每1列表示1幅不同光照强度下的人脸图像，即数据中共包含人脸图像20幅。要求将这20幅图分成2类，具体情形如图4所示。

表3给出了在不同最终降维数下，MRPKPCA模型、标准的MPKPCA模型和KFC-M的平均聚类准确率以及平均完全聚类准确率，另外2个参数都是在调试后较优的情况下给出的。

将完全聚类准确率定义为：

图4　不同光照强度下的人脸图像Fig.4 Face image under different illumination intensity

表3　不同最终降维数下的θ和值Tab.3 Values ofθandin different final number of dimensionality reduction

表3　不同最终降维数下的θ和值Tab.3 Values ofθandin different final number of dimensionality reduction

？

对表3中所示结果进行分析可知，在对模型的各参数进行优化后，与MPKPCA模型、KFC-M算法相比，MRPKPCA模型有着较高的聚类准确率，且聚类完全正确的比率也较高。因此，可知MRPKPCA模型在对小样本数据进行聚类分析时，有着较好的鲁棒性和较高的准确率。

4　结束语

经典的PCA方法是一种已被证明的有效的探索数据聚类和数据可视化的基础性的工具。但用于处理实际问题时，由于实际数据往往为非线性、存在噪声和异常点的混合数据，因此，将其进行拓展是必不可少的。本文提出的鲁棒概率核主成分分析模型，首先，将数据映射到高维核空间，将非线性数据进行线性化；然后，在高维核空间中，将经典PCA方法与基于高斯隐变量模型的极大似然框架相结合，利用了样本本身的分布来提高结果的准确率。同时，用t分布作为先验分布，增强了模型的鲁棒性，减少了异常点的影响。并且，在实验测试中，通过与经典MPKPCA模型、KFC-M算法进行比较，可看出MRPKPCA模型有着较高的准确率。所以，MRPKPCA模型在数据降维和聚类方面是有效的。

本文所建的MRPKPCA模型并未考虑求得的主成分中包含异质主成分的情况，且模型的自由参数过多，下一步将修改模型以解决这些方面的问题。

［1］SHAHID N，PERRAUDIN N，KALOFOLIAS V，et al. Fast robust pca on graphs［J/OL］.ArXiv Preprint，2015：1507.08173.

［2］GUPTA B.Analyzing face recognition using principal component analysis［J］.Akgec International Journal of Technology，2009，5（1）：5-8.

［3］BRO R，SMILDE A K.Principal component analysis［J］. Analytical Methods，2014，6（9）：2812-2831.

［4］UDELL M，HORN C，ZADEH R，et al.Generalized low rank models［J/OL］.ArXiv Preprint，2014：1410.0342.

［5］WANG Y，JIANG Y，WU Y，et al.Spectral clustering on multiple manifolds［J］.IEEE Transactions on Neural Networks，2011，22（7）：1149-1161.

［6］SHAHID N，KALOFOLIAS V，BRESSON X，et al.Robust principal component analysis on graphs［C］//Proceedings of the IEEE International Conference on Computer Vision.Chile：IEEE，2015：2812-2820.

［7］TIPPING M E，BISHOP C M.Mixtures of probabilistic principal component analyzers［J］.Neural Computation，1999，11（2）：443-482.

［8］SU T，DY J G.Automated hierarchical mixtures of probabilistic principal component analyzers［C］//Proceedings of the Twenty-first International Conference on Machine Learning.Canada：ACM，2004：98.

［9］ZHAO J.Efficient model selection for mixtures of probabilistic PCA via hierarchical BIC［J］.IEEE Transactions on Cybernetics，2014，44（10）：1871-1883.

［10］FILIPPONE M，CAMASTRA F，MASULLI F，et al.A survey of kernel and spectral methods for clustering［J］. Pattern Recognition，2008，41（1）：176-190.

［11］SCHÖLKOPF B，SMOLAA，MÜLLER K R.Kernel principal component analysis［C］//Artificial Neural Networks-ICANN'97.Berlin：Springer，1997：583-588.

［12］DING X，HE L，CARIN L.Bayesian robust principal component analysis［J］.IEEE Transactions on Image Processing，2011，20（12）：3419-3430.

［13］CANDÈS E J，LI X，MA Y，et al.Robust principal component analysis［J］.Journal of theACM，2011，58（3）：11.

［14］WRIGHT J，GANESH A，RAO S，et al.Robust principal component analysis：exact recovery of corrupted lowrank matrices via convex optimization［C］//Advances in NeuralInformationProcessingSystems.Vancouver，2009：2080-2088.

［15］XU H，CARAMANIS C，SANGHAVI S.Robust PCA via outlier pursuit［C］//Advances in Neural Information Processing Systems.Vancouver，2010：2496-2504.

［16］ZHOU S.Probabilistic analysis of kernel principal components：mixture modeling and classification［C］//Submitted to IEEE Transactions on Pattern Analysis and Machine Intelligence.IEEE，2003：1-26.

［17］ARCHAMBEAU C，DELANNAY N，VERLEYSEN M. Mixtures of robust probabilistic principal component analyzers［J］.Neurocomputing，2008，71（7）：1274-1282.

［18］JIANG L，ZENG B，JORDAN F R，et al.Kernel function and parameters optimization in kica for rolling bearing fault diagnosis［J］.Journal of Networks，2013，8（8）：1913-1919.

［19］VEMULAPALLI R，PILLAI J，CHELLAPPA R.Kernel learning for extrinsic classification of manifold features ［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Portland：IEEE，2013：1782-1789.

［20］LIU C，RUBIN D B.ML estimation of the t distribution using EM and its extensions，ECM and ECME［J］.Statistica Sinica，1995，5（1）：19-39.

［21］SHY SHOHAM.Robust clustering by deterministic agglomeration EM of mixtures of multivariate t distributions ［J］.Pattern Recognition，2002，35（5）：1127-1142.

［22］SHOHAM S，FELLOWS M R，NORMANN R A.Robust，automatic spike sorting using mixtures of multivariate t-distributions［J］.Journal of Neuroscience Methods，2003，127（2）：111-122.

［23］PEEL D，MCLACHLAN G J.Robust mixture modellingusing the t distribution［J］.Statistics and Computing，2000，10（4）：339-348.

［24］NOCEDAL J，WRIGHT S.Numerical optimization［M］. Berlin：Springer，2000：10-54.

［25］LICHMAN M.UCI machine learning repository［Z/OL］.（2013-07-01）［2016-05-21］.http：//archive.ics.uci.edu/ml/ datasets.html.

［26］周巧萍，潘晋孝，杨明.基于核函数的混合C均值聚算［J］.模糊系统与数学，2008，22（6）：148-151. ZHOU QIAOPING，PAN JINXIAO，YANG MING.Hybrid clustering algorithm based on the kernel function［J］. Fuzzy Systems and Mathematics，2008，22（6）：148-151.（in Chinese）

［27］MINISTRY OF EDUCATION AND GRADUATE EDUCATION DEVELOPMENT CENTER.2015 National graduate student contest［Z/OL］.（2015-06-15）［2016-05-21］.http：//www.shumo.com/home/html/3179.html.

A Robust Probabilistic Kernel Principal Component Analysis Model

YANG Yuna，LI Biaob，WANG Shuaileia
（Naval Aeronautical and Astronautical University a.Graduate Students’Brigade；b.Department of Basic Sciences，Yantai Shandong 264001，China）

The dimension of the processed data have become more and more higher，so dimensionality reduction becomes more and more important.The classical PCA（Principal component analysis）has proven to be an effective dimensionality reduction method.But its effect was poor when used it to disposing nonlinear，noise and outliers data set，so，a robust probabilistic kernel principal component analysis model（RPKPCA）was proposed.It combined kernel method with maximum likelihood frame based on Gaussian process latent variable model and used t-distribution as prior distribution to solve its three disadvantages at the same time.In addition，a mixtures of robust probabilistic kernel principal component analysis model（MRPKPCA），and it could be used directly to dimensions reduction and data mining of mixture and nonlinear data. The experimental results in different data set showed that the model of proposed in this paper had higher accuracy than the standard probabilistic kernel principal component analysis model.

principal component analysis；dimensionality reduction of robustness；EM algorithm；cluster analysis；kernel method；latent variable model

TP391.41

A

1673-1522（2016）04-0415-08

10.7682/j.issn.1673-1522.2016.04.003

2016-05-26；

2016-06-28

杨芸（1991-），男，硕士生。