多指数连续相位调制信号的早迟环定时同步*
谢顺钦,谢 滔,钟 声,杨 春,王世练,张 健
(1.中国工程物理研究院 电子工程研究所, 四川 绵阳 621000;2.国防科技大学 电子科学与工程学院, 湖南 长沙 410073)
多指数连续相位调制信号的早迟环定时同步*
谢顺钦1,谢滔2,钟声1,杨春1,王世练2,张健1
(1.中国工程物理研究院 电子工程研究所, 四川 绵阳621000;2.国防科技大学 电子科学与工程学院, 湖南 长沙410073)
针对多指数连续相位调制信号提出基于序列检测的早迟环定时同步,利用维特比算法的幸存度量构造定时误差估计器。根据误差估计的S曲线和方差,优化定时误差捕获范围和估计精度、消除环路假锁点,同时利用多指数连续相位调制的脉冲幅度调制分解对定时误差估计器进行简化。仿真结果表明,优化后的早迟环定时误差捕获范围最大可达±0.5个符号周期,估计精度在中低信噪比下能够接近修正的克拉美罗界,在高信噪比下也有较好的估计性能;当早迟环定时支路的分支度量简化至最大似然序列检测的1/8时,对多进制、部分响应的多指数连续相位调制信号,造成的解调性能损失小于0.5 dB。
多指数连续相位调制;定时;早迟环;S曲线;克拉美罗界
连续相位调制(Continuous Phase Modulation,CPM)是一种高带宽效率的恒包络调制[1]。多调制指数CPM相比单指数CPM增大了最小欧氏距离,提高了误码性能。美国先进靶场遥测组织在遥测标准IRIG106-04[2]中就将多指数CPM信号定义为新一代的遥测信号。然而CPM信号存在两大难点——同步困难及解调复杂度高。尤其是对频谱效率更高的高阶调制、部分响应的CPM信号,信号相位的高度平滑性导致同步参数估计更加困难。目前,CPM已有的定时同步算法主要包含数据辅助(Data-Aided, DA)[3]、非数据辅助(Non-Data-Aided, NDA)[4]及面向判决(Decision-Directed, DD)[5-6]等方法。其中,DA同步精度最高,但是同步头会导致传输功率的浪费;NDA定时同步虽然定时误差捕获范围大、对载波相位不敏感,但对高进制、部分响应长度大的CPM信号的估计精度差[7]。DD定时的性能一般介于NDA和DA定时之间,但是当判决结果来自最大似然序列检测(Maximum Likelihood Sequence Detection, MLSD)时,其定时精度可达到DA同步的精度。但对于高进制、部分响应长度大的CPM信号,DD定时的定时偏差捕获范围小,并存在假锁问题[8-9]。虽然DD定时可以联合NDA定时来克服假锁问题[8],但“假锁检测—引导—重新锁定”的定时策略会大大增加定时捕获的时间。早迟门定时同步[10]为线性调制系统中广泛采用的定时方法,利用相关器输出的对称特性构造定时误差估计器(Timing Error Detector,TED)。Glisic最早将早迟环应用于部分响应的CPM信号[11],但指出由于部分响应CPM存在符号间干扰,因此不适宜用基于逐符号估计的早迟门定时环路。
最近的文献[12]给出了二进制多指数CPM信号基于序列检测的早迟门定时同步,算法利用似然函数的凸函数性构造TED,采用分块估计、迭代调整的方式完成定时恢复。将该方法应用于Tier2这类四进制多指数CPM时,似然函数的凸函数特性会被破坏。另外,迭代调整的方式虽然能缩短捕获时间,但此时估计精度也较差。最后,高复杂度是基于序列检测的早迟门定时面临的最关键问题之一,文献[12]并没有进一步讨论。本文将针对定时更困难的四进制、多指数CPM,设计和优化了基于序列检测的早迟环定时。最后从降低序列检测的复杂度入手,在保证早迟环定时精度的同时,使得复杂度得到了大幅降低。
1 系统模型
1.1信号模型及PAM分解
CPM信号的基带信号可以表示为[1]:
(1)
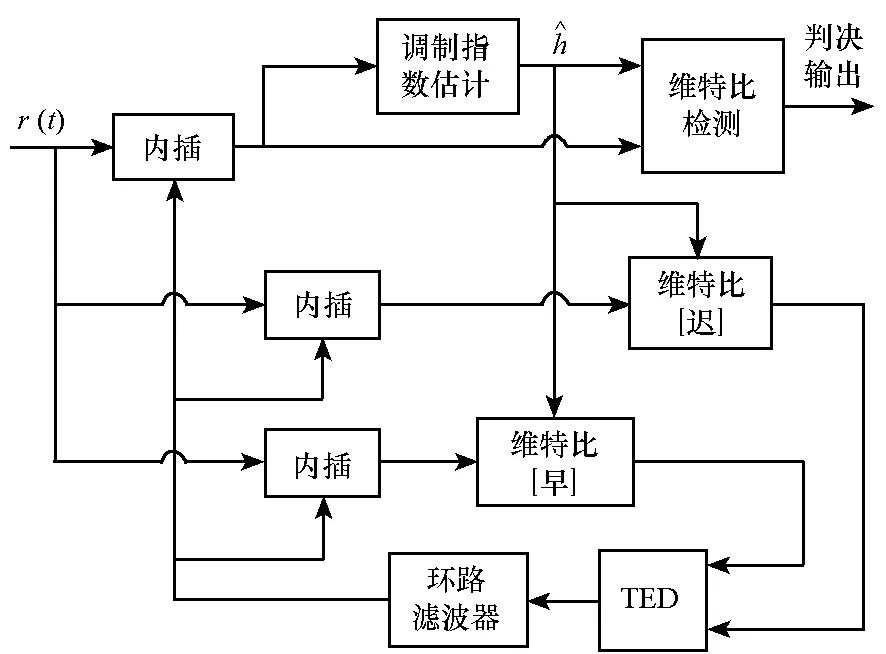
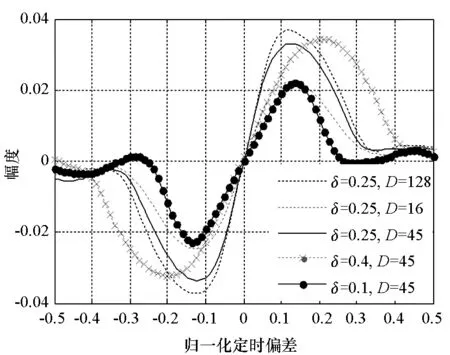
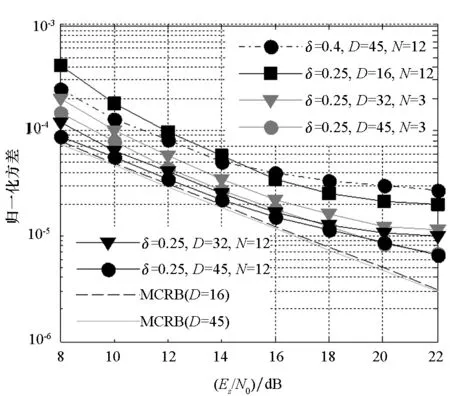
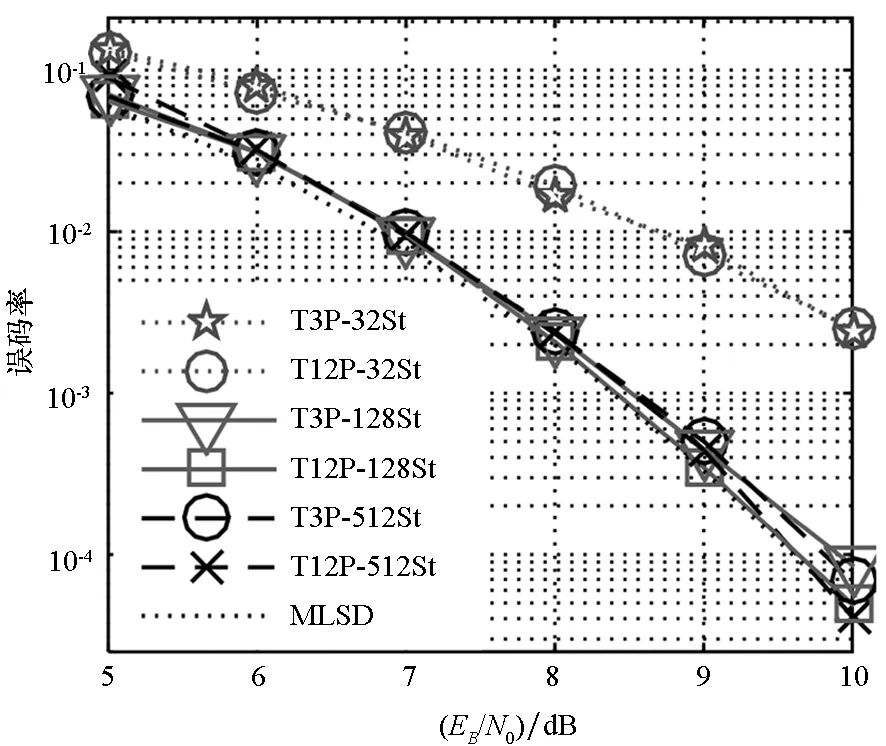
其中,Es为一个符号间隔内的信号能量,T为符号周期,ψ(t)为CPM信号的相位,在第n个符号间隔(nT≤t (2) 其中,αi∈{±1,±3,…,±(M-1)},M为调制进制数,hi为i时刻对应的调制指数,q(t)为CPM频率脉冲g(t)的积分,g(t)通常为升余弦脉冲(Raised Cosine pulse, RC)、矩形脉冲(RECtangular pulse, REC)等,g(t)非零部分的长度为L,即CPM信号的部分响应长度。本文针对M=4,L=3,g(t)为RC,h=[4/16,5/16]的多指数CPM信号,即ARTM Tier Ⅱ信号,简称Tier2信号。 多指数CPM的脉冲幅度调制(Pulse Amplitude Modulation, PAM)分解由Perrins给出[6]: (3) 1.2多指数CPM接收模型 多指数CPM基于早迟环定时的接收框图如图1所示,图中已假设载波得到了理想同步。接收信号分三路进行内插,得到早、迟支路和解调支路,并分别通过维特比算法作MLSD。早、迟支路的幸存度量用于TED的定时误差估计,估计误差经环路滤波后得到内插控制参数,分别用于控制三个支路的内插器。多指数CPM信号进行MLSD前需要先进行调制指数同步,当早、迟支路与解调支路的时延较短(本文中通常不大于T/4)时,三个支路共享同一个调制指数的同步信息。调制指数同步模块限于篇幅此处不再介绍。 图1 简化的多指数CPM接收机框图Fig.1 Simplified block diagram of multi-h CPM receiver 2.1基于PAM分解的最大似然序列检测 CPM信号为有记忆调制信号,其最佳检测器为最大似然序列检测[1]器。设在高斯白噪声(Additive White Gaussian Noise, AWGN)信道下接收的复基带信号(定时偏差为τ): r(t)=s(t-τ)+n(t) (4) (5) (6) 其中,s*(t)表示s(t)的复共轭。将式(3)代入式(6),并采用维特比算法将度量计算分解为递归形式,可得到基于PAM分解的MLSD分支度量递推表达式[13]为: (7) (8) (9) MLSD通过幸存路径回溯进行序列判决,在实际应用中,考虑到判决延时,在不影响性能的前提下回溯深度(Dtb)应尽量小,通常取5倍相关长度[10],即Dtb=5log2(numState),numState为序列检测器的维特比状态数。对于Tier2信号,最佳MLSD检测器为512状态,因此回溯深度一般取Dtb=45。 2.2基于超前滞后采样的TED 接收信号r(t)分别作超前和滞后δT/2的采样(内插),经过PAM脉冲滤波得到采样输出: (10) (11) 幸存度量的最大值即为早迟支路的最大幸存度量: (12) D为定时支路度量的累积深度,与式(9)不同的是,这里用于求最大值的度量为(iD+1)T时刻至(iD+D)T时刻的分支度量累积值,该度量每隔DT清零一次,因此式(12)得到的是一段时间内的最大幸存度量。图2为Tier2信号在不同定时偏差τ下,通过式(9)和式(12)得到的最大度量曲线(δ=0.25,D=45)。 图2 三支路的最大幸存度量Fig.2 Maximum survival metrics of 3 branches 从图2可以看出,MLSD支路的最大似然度量曲线是对称的,在τ=0处有最大值。这与文献[12]的结果类似,但是度量值在定时误差大于0.2以后曲线出现了平缓区,因此Tier2信号的度量并不是定时误差的凸函数。早、迟支路的最大幸存度量实际为最大似然度量曲线分别左、右移了δT/2。二者在τ=0的点相等,并在(-0.5T,0)或(0,0.5T)定时偏差下,有一致的大小关系(如在定时偏差为0~0.5T时,迟支路度量始终比早支路度量大)。因此可以通过式(12)的两个度量差提取定时误差: (13) 统计不同定时偏差τ下的定时误差均值,将得到定时误差估计的S曲线S(τ)。 2.2.1早迟支路间隔δ及累积深度D的选取 定时S曲线能够反映定时环路的工作特性[7]:首先,除了τ=0的过零点外,S曲线最近的过零点决定了定时环路的捕获范围。其次,环路工作机制决定了S曲线在τ=0处的斜率越大,环路工作的精度越高。因为此时轻微的偏差会导致较大的负反馈调整量,使得环路更快调整到误差为0的点。最后,若除了τ=0的过零点外还存在其他斜率为正的过零点,则为环路工作的假锁点[8-9]。因此可以通过S曲线的相关特性优化定时参数,不同的早迟支路间隔δ和累积深度D下的S曲线如图3所示。 图3 不同δ和D的定时S曲线Fig.3 Timing S-curve with different δ and different D 由图3可以看出,不同的δ对定时的捕获范围和精度都影响较大,当固定D为45时,从图中δ分别为0.1,0.25和0.4的曲线来看,δ=0.1的S曲线在τ=±0.35T附近有正斜率的过零点,从而该δ取值会导致假锁的发生。δ为0.4和0.1的S曲线的过零点斜率都比δ为0.25的斜率小,这说明这两种取值都比δ=0.25的精度差。 当固定δ=0.25时,从图中可以看出累计深度D的取值对S曲线的影响相对于δ的影响要小得多。但从图中仍可看出,一方面当D小于45较多,如图中的D=16时,S曲线过零点的斜率会明显变小,说明较小的D值会影响到定时精度;另一方面D=128与D=45时的S曲线表明二者的捕获范围和估计精度差别不大。但考虑到大的D值会增大环路调整的时延,因此综合考虑精度和延时后,D可与解调支路的判决回溯深度Dtb一致,都为45。 2.2.2基于PAM分解的定时简化 基于序列检测的早迟环定时算法需要对超前、滞后支路采用维特比算法计算幸存度量,因此若定时支路也采用MLSD,整个解调端需要承受3个MLSD的复杂度。这对于Tier2等多指数CPM信号,在实际应用中将会占用巨大的硬件资源,因此需要对早迟环定时的降复杂度方法进行研究。 基于PAM分解的减复杂度检测[13]及DD定时算法[9],都能在性能损失较小的前提下,大幅降低算法复杂度,本文也将采用PAM分解简化早迟环定时。Tier2信号的PAM分解共48个脉冲(不区分奇偶时刻),通常采用小于48的脉冲组合进行信号近似,以简化复杂度。对于Tier2信号的序列检测,除了48个脉冲(512状态)的最佳MLSD,主要有以下三种简化方法[14]:第一种为取第一个能量最大的脉冲,此时状态数简化为32;第二种为取前3个能量最大的脉冲,此时状态数简化为32;第三种为取前12个能量最大的脉冲,此时状态简化为128。其中第一种简化由于较大的能量损失,序列检测的性能损失也比较大,因此该简化方法一般不采用。此外,其他脉冲组合(除了1,3,12外)由于脉冲能量的分布特性,一般也不予采用。若解调支路采用性能与MLSD相当的128状态简化序列检测,定时支路采用第二种和第三种简化方法,三支路的总度量数可由6144分别简化为768和1536,即分别降低为原来的1/8和1/4,从而大大降低了系统复杂度。 环路收敛后的性能评价可以通过与修正的克拉美罗界(Modified Cramer-Rao Bound, MCRB)作比较。频率响应脉冲为RC的CPM定时估计归一化MCRB为[7]: (14) L′0=L0+D+DPAM (15) 其中,L0=1/(2BLT)为环路归一化带宽BLT决定的相关符号数,DPAM为PAM分解脉冲的最大长度,对Tier2信号DPAM=4。通常L0≫D+DPAM,此时不同的D导致的MCRB近似相同,因此可以将不同D的MCRB放在一起比较。 采用一阶定时环[7],定时NCO输入为: η(n+1)=η(n)+γτe(n) (16) 其中,e(n)为TED输出的误差估计值,γτ为一阶环路带宽的控制系数,与归一化环路带宽BLT的关系为: (17) 其中kpt为定时估计S曲线S(τ)在τ=0处的斜率。 通过MATLAB对估计的方差进行仿真,参数设定为:Ns=8,τ=7T/16(大于0.4),总仿真符号数为5×105,归一化环路带宽BLT=1×10-3,并在10 000个符号后开始统计(此时环路一般已收敛)。其他用于比较的变量有:定时支路采样间隔δ,累计符号数D,以及PAM分解脉冲数N。由2.2.1节的参数优化过程及2.2.2节的简化方法讨论,主要针对δ为0.25,D为32和45,以及PAM脉冲数为3和12的情况进行仿真。同时为了比较δ=0.4以及D=16的性能,还列出了[δ,D,N]为[0.4,45,12]以及[0.25,16,12]的估计方差曲线。此外,Tier2信号的定时估计MCRB也列于其中作理想估计性能的参考,仿真结果如图4所示。 由图4可以看出,δ为0.4的估计精度比0.25时要差,这与通过S曲线的分析一致。其次,D越大精度越高,且随着信噪比的增大,D=16和32的情况比D=45时差距越来越大,这说明幸存度量的可靠性随着D的增大而变高,从而能提高估计的性能。对于不同的复杂度简化方案,N=3的估计精度虽然比N=12略差,但是差距不大,特别在信噪比较高时,二者的差距很小。此外,图4还表明δ=0.25,D=45,N=12的定时精度在Es/N0<14 dB(此时对应的Eb/N0为11 dB)的信噪比下性能接近MCRB,在大于14 dB的信噪比下精度与MCRB相差不大。 值得指出的是,δ=0.25及D=45的取值都是有一定实用价值的:首先,δ=0.25时,早、迟支路都与解调支路相差1个采样间隔(每个符号过采样数Ns=8),早、迟支路数据可通过解调支路的内插器获取,简化了实现的结构。其次,D=45为维特比算法的推荐判决延时,该累积深度下得到的幸存路径度量有足够的可靠性,同时定时误差的变化在实际应用中通常是缓变过程,在该判决延时下得到的定时误差估计值的实时性能够得到保证。 图4 估计方差仿真结果(BLT=10-3)Fig.4 Variance of timing estimation(BLT=10-3) 进一步固定δ=0.25及D=45,对不同的简化定时及简化序列检测(解调支路,下同),得到误码性能如图5所示。图中“TmP-nSt”表示定时的简化PAM脉冲数为m、序列检测的简化状态数为n的联合简化方法。其中“32St”及“128St”分别表示3个PAM简化(32状态)和12个PAM简化(128状态)的序列检测,“512St”为未简化的最佳序列检测,“MLSD”为理想定时下的性能界。 图5 Tier2信号的解调性能Fig.5 Demodulation performance for Tier2 从图5可以看出,在相同的序列检测复杂度下,基于3个PAM和12个PAM的简化定时方法带来的性能差异很小:①32状态序列检测下,两个定时算法的性能差异可忽略,但都与MLSD的性能相差较大,这主要是由于解调本身而非定时带来的损失;②128状态和512状态序列检测下,3PAM定时相对12PAM定时的性能损失小于0.5 dB,其中12PAM定时下的性能相比MLSD的性能损失可忽略。 基于最大似然序列检测的幸存路径度量差,构造和优化了多指数CPM的早、迟环定时同步。通过对ARTM Tier2信号的仿真表明,本文设计的早、迟环定时有最大可达±0.5T的误差捕获范围,同时有较高跟踪精度——在符号信噪比小于14 dB的中低信噪比下能够接近修正的克拉美罗界。利用多指数CPM的PAM分解,早、迟环定时在保证精度的同时能大幅降低复杂度。如基于3 PAM脉冲的简化定时及128状态的简化序列检测,总分支度量数降低为简化前的1/8,相比MLSD的性能损失却小于0.5 dB。 需要指出的是,本文与文献[12]相比有更高的精度和更多降复杂度的考虑,且捕获时间相对更长。因此可以从捕获时间的角度对早迟环定时进一步优化,如在捕获和跟踪阶段采用不同环路带宽的方法。另外,本文只利用了多指数CPM的PAM分解作简化,下一步还可联合采用其他算法(如倾斜相位模型[15]、减状态序列检测[16]等),降低早迟环定时的复杂度。 References) [1]Anderson J B, Aulin T, Sundberg C E. Digital phase modulation [M]. New York,USA: Plenum, 1986. [2]Council R C. Telemetry standards [M]. New Mexico: Range Commanders Council, 2004. [3]Huber J, Liu W. Data-aided synchronization of coherent CPM-receivers [J]. IEEE Transactions on Communications, 1992, 40(1): 178-189. [4]D′Andrea A N, Mengali U, Morelli M. Symbol timing estimation with CPM modulation [J]. IEEE Transactions on Communications, 1996, 44(10): 1362-1372. [5]Morelli M, Mengali U, Vitetta G M. Joint phase and timing recovery with CPM signals [J]. IEEE Transactions on Communications, 1997, 45(7): 867-876. [6]Perrins E, Rice M. PAM decomposition of M-ary multi-h CPM [J]. IEEE Transactions on Communications, 2005, 53(12): 2065-2075. [7]Mengali U, D′Andrea A N. Synchronization techniques for digital receivers [M]. New York & London: Plenum Press, 1997. [8]Perrins E. A timing false lock detector for m-ary partial-response CPM [J]. IEEE Wireless Communications Letters, 2013, 2(6): 671-674. [9]Perrins E, Bose S, Wylie-Green M P. Timing recovery based on the PAM representation of CPM [C]// Proceedings of the Military Communications Conference, 2008 MILCOM 2008 IEEE, San Diego, CA, 2008: 1-8. [10]Proakis J G. Digital communications [M]. New York: McGraw-Hill, 2008. [11]Glisic S G. Symbol synchronization in digital communication systems using partial response CPM signaling [J]. IEEE Transactions on Communications, 1989, 37(3): 298-308. [12]张金荣, 吴岭, 朱宏权. Multi-h CPM遥测信号的定时频率联合估计技术 [J]. 飞行器测控学报, 2014, 33(6): 485-490. ZHANG Jinrong, WU Ling, ZHU Hongquan. Joint symbol timing and frequency synchronization technology for multi-h CPM telemetry signal[J]. Journal of Aircraft Measurement and Control, 2014, 33(6): 485-490.(in Chinese) [13]Perrins E, Rice M. Optimal and reduced complexity receivers for M-ary multi-h CPM [C]// Proceedings of the Wireless Communications and Networking Conference, 2004 WCNC 2004 IEEE, Atlanta, GA, 2004, 2: 1165-1170. [14]Perrins E, Rice M. Reduced-complexity detectors for multi-h CPM in aeronautical telemetry [J].IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 286-300. [15]Rimoldi B E. A decomposition approach to CPM [J]. IEEE Transactions on Information Theory, 1988, 34(3): 260-270. [16]Svensson A. Reduced state sequence detection of partial response continuous phase modulation [J]. IEE Proceedings I,Communications, Speech and Vision, 1991, 138(4): 256-268. Timing synchronization based on early/late loop with multi-h continuous phase modulation XIE Shunqin1, XIE Tao2, ZHONG Sheng1, YANG Chun1, WANG Shilian2, ZHANG Jian1 (1. Institute of Electronic Engineering, China Academy of Engineering Physics, Mianyang 621000, China; 2.College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China) Timing synchronization with the early/late loop scheme based on sequence detection was proposed for multi-h continuous phase modulation. The timing error detector was implemented by the survival metrics of Viterbi algorithm. The so-called S-curve and estimation variance were used for optimizing the acquisition range and tracking performance as well as eliminating false lock points of the loop. Using the PAM (pulse amplitude modulation) representation of multi-h CPM(continuous phase modulation), the proposed timing error detector is simplified. Simulation results show that the estimation range is as large as ±0.5 symbol period, and estimation precision is close to the modified Cramer-Rao bound at medium and low SNR(signal noise ratio), and it also has better estimation performance at high SNR. BER (bit error rate) with simplified schemes are derived. It is demonstrated that when the number of Viterbi metrics is reduced to 1/8 of the maximum likelihood sequence detection, the performance loss is only less than 0.5 dB for M-ary or partial response of multi-h CPM. multi-h continuous phase modulation; timing synchronization; early-late gate; S-curve; Cramer-Rao bound 10.11887/j.cn.201604018http://journal.nudt.edu.cn 2015-05-07 国家自然科学基金资助项目(61501484);国防预研基金资助项目(9140A25031013KG01359) 谢顺钦(1987—),男,贵州贵定人,博士研究生,E-mail:suntrain@163.com;张健(通信作者),男,研究员,博士,博士生导师,E-mail:suntrain@caep.cn TN95 A 1001-2486(2016)04-113-06
2 算法描述
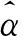
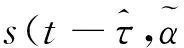

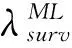

3 性能仿真

4 结论

