平底气泡船凹槽气层波动特性*

吴　浩，欧勇鹏

(海军工程大学 舰船工程系， 湖北 武汉　430033)



平底气泡船凹槽气层波动特性*

吴浩，欧勇鹏

(海军工程大学 舰船工程系， 湖北 武汉430033)

为提高大型平底气泡船底部凹槽设计的有效性，基于RANS方程及VOF两相流模型构建了大型平板船凹槽气层数值计算模型。研究气层在凹槽中的动态发展过程，分析速度对气层波动的影响规律，并阐述三维凹槽气层的波形特性及其与二维气层波动的区别，揭示气层波动的相似律。数值结果表明：气层在凹槽中呈现波动形态，气层波长随速度的增加而增大，波长等于速度平方的0.64倍；气层在凹槽侧壁的干扰及反射下呈现相干波系，从而其波高及局部厚度也随之改变；气层波动满足傅汝德相似。

平板船；波动形态；回归分析；相似律；VOF模型

相同航速下，气层减阻技术应用在高速船可节省20%～30%的主机功率，应用在排水型船可节约主机功率10%～20%[1-3]，而设计优良的供气系统产生减阻气层需要消耗的功率小于主机功率的3%[4-5]。

船底凹槽是排水型船舶气层减阻方案设计的重要途径。荷兰DK Group船舶设计公司针对大中型运输船型，通过在船底设置大型凹槽，开发了气层减阻系统(air cavity system)，在超大型原油轮(Very Large Crude Carrier, VLCC)模型上采用该系统后阻力降低15%以上。2008年，该公司在一条长81 m、宽13.4 m、吃水5.8 m、设计航速12 kn、载重量2800 t的小型散货船上进行了实船气层减阻改装及测试，航行试验表明：总体节能效果可达到8%[6]。苏联的克雷洛夫中央舰船研究院针对大型油船、货船、高速客船、登陆艇、滑行艇等常规船型及双体船、多体船开展了较为系统的研究，通过在船底设置单个或多个凹槽，先后完成了40多型采用气穴减阻技术的船舶设计方案，已有70多条排水量14～280 t的气泡船投入运营，航速在30～52节之间，广泛用于巡逻、登陆、护卫、缉私、反恐及民用高速运输等领域[7-11]。Zverkhovskyi等[12-13]针对一条长2 m，宽0.298 m的平板开展了试验研究，并在平板两侧安装了侧板，试验结果表明：在两侧安装侧板可以延长平板底部的气层长度。蔡泽伟等[14]在计算水面舰艇的水动力导数时引进了细长体假定，将三维的流动问题简化为了二维的非定常问题。Butuzov[15]针对气泡高速艇发展了线性2D理论，分析结果表明：速度一定时，存在一个气穴的极限长度，当气穴长度超过该极限长度时，舰艇理论上不可能保持稳定状态。该理论为气泡高速艇艇型参数设计及优化提供了依据。Kim等[16]采用直接数值模拟(Direct Numerical Simulation, DNS)的方法计算了断阶后气层的非定常流动形态，计算结果表明较大的气流量利于形成稳定的气层，这与试验结果吻合，但是采用该方法计算量较大，不适用于计算气泡船喷气减阻方案对比或船型优化。

1　数值方法

1.1黏性流场控制方程及湍流模型

RANS方程是黏性流场运动学和动力学的控制方程，主要包括连续性方程和动量方程，具体形式为：

(1)

(2)

式中:ρm为流体密度；vm为流体速度；μ为流体黏度；p为静压；fi为单位质量力；ui，uj为速度分量。

湍流模型采用RNGk-ε模型，具体形式如下。湍流脉动动能方程(k方程)为：

(3)

湍流能量耗散率方程(ε方程)为：

(4)

1.2VOF多相流模型

VOF模型依靠的是两种或多种流体(或相)没有互相穿插这一事实。对增加到模型里的每一附加相，都引进一个变量：即计算单元里的相的体积分数。在每个控制单元格内，所有相的体积分数之和为1。此时只要知道局部单元格中不同相的体积分数，即可通过求解获得该单元网格中的流场参数值，并通过利用体积分数对输运方程中的密度、黏度等进行修正，从而获得流场混合相的控制方程：

(5)

式中，αq表示第q相在某单元格中的体积分数。当αq=0时表示该单元格中不含第q相；当αq=1时表示该单元格中全部被q相占满；当0<αq<1时表示该单元格中存在分界面。在计算过程中，相与相之间的分界面是通过求解如式(6)所示的体积分数方程获得的。

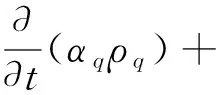
(6)

主流相的体积分数并非通过求解式(6)获得，而是通过式(7)求解得到。

(7)

分界面采用几何重构法进行可视化显示，该方法假设分界面在每个网格中是呈线性的，然后利用该分段线性边界重新构造流体分界面。

1.3计算模型

计算模型为平板船，图1给出了平板船模型示意图。模型总长8.19 m，宽1.71 m，厚0.06 m，平板首部及尾部呈流线型，在平板底部设置凹槽，凹槽长Lh为7.59 m，研究过程中，凹槽深度h可变。凹槽面积与平板下表面的面积之比为0.921，与平板的湿表面积之比为0.461。凹槽尾部设置向后倾斜13.13°的斜坡结构。在凹槽首部设置喷气装置，空气垂直喷入。

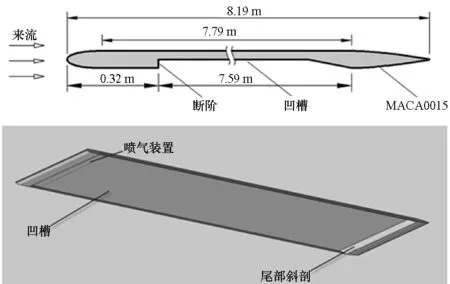
图1　平板船模型示意图Fig.1　Model of flat plate ship

图2给出了计算区域的网格划分及边界条件设置。平板位于水面以下1 m水深处，处于正浮状态，平板流场关于中纵剖面对称，因此仅需对实际流场的一半进行数值求解。计算域总长为3倍板长，入口距离平板首部0.6倍板长，设置为速度入口；出口距离尾部1.4倍板长，设置为静压出口；流场上下边界、侧面边界距离平板0.8倍板长，设置为无摩擦壁面，中纵剖面设置为流场对称面。喷气入口位于凹槽的首部，垂直于凹槽底面向外喷气。流场区域采用全结构化网格进行离散，网格总数为160万，在距离平板表面0.5 m的区域内对网格进行加密，加密区域与外流场之间采用插值面进行过渡。

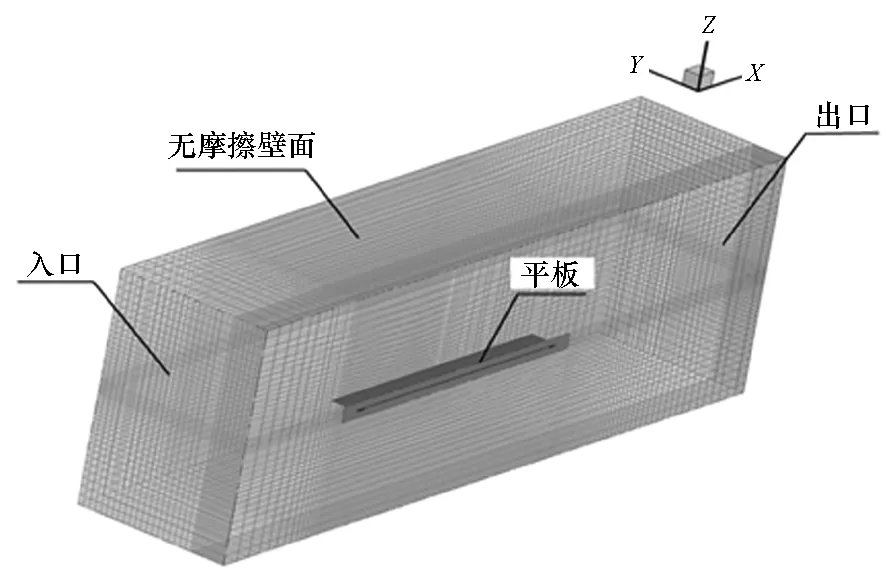
图2　计算网格及边界条件Fig.2　Calculation field mesh and boundary conditions

2　计算结果及分析

2.1气层动态特征

定义凹槽长度傅汝德数Fn和无因次气流量系数Cq为：

(8)

(9)

其中，Lh表示凹槽的长度，h表示凹槽深度，b表示凹槽宽度(在二维流场中取b=1)，V表示来流速度，Q表示气流量。

图3给出了Fn=0.207，Cq=0.148，h=0.46%Lh时气层在二维凹槽中的形成过程(为了清晰地显示气层形态，将图像长度方向的尺寸缩小为原来的1/5)。由图3可知：向凹槽首部喷气，在喷孔处会迅速形成局部空穴；当喷气时间t≤8.5 s时，空穴面积较小，气体向后缓慢延伸；当t>8.5 s时，气体迅速延伸至凹槽尾部；当t>14.5 s时，继续向凹槽中喷气，气层平均厚度逐渐增大；当t=23.5 s时，气层边界呈现出较明显的波动状态；当t=29.5 s时气层形态基本稳定，气体从凹槽尾部向外溢出。

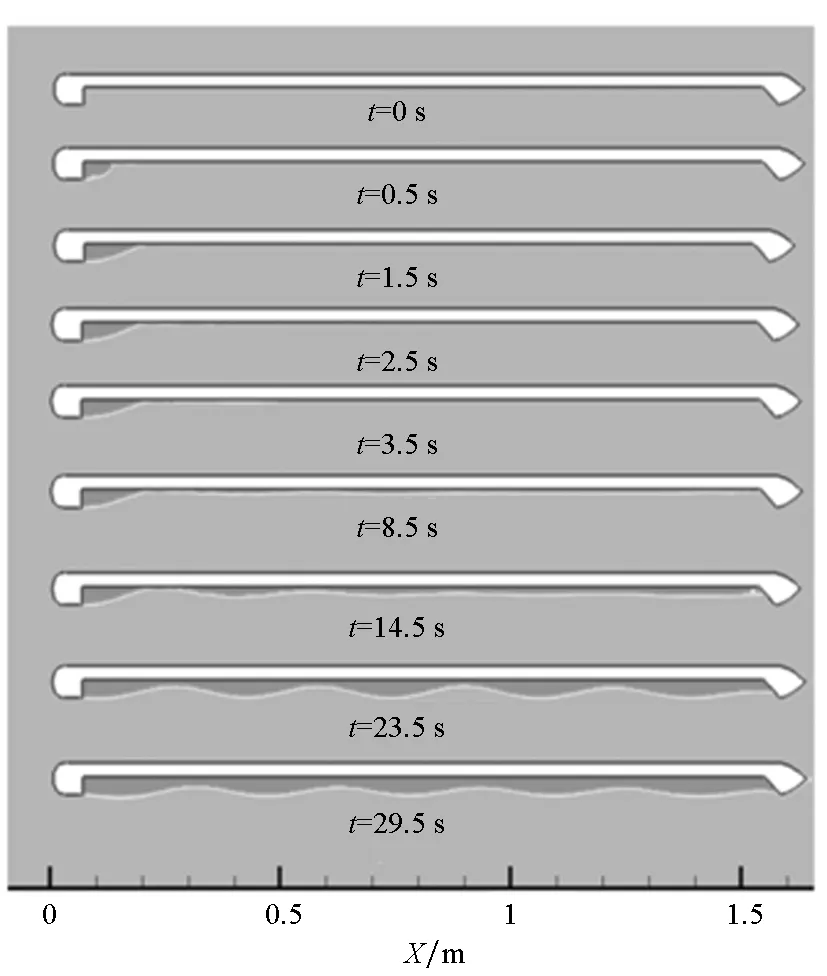
图3　凹槽中气层的发展过程Fig.3　Evolution of air layer on bottom hollow

图4给出了t=29.5 s时气层边界的波动形态，图中Y轴坐标的0点处对应凹槽首部断阶的下边缘，Y<0表示气层突出了凹槽之外。由图4可知：在凹槽首部，气层边界首先向下运动形成波谷，之后周期性波动向后延伸，在尾部与凹槽斜坡接触形成封闭空腔，将平板凹槽内下表面与水流完全隔离开来。

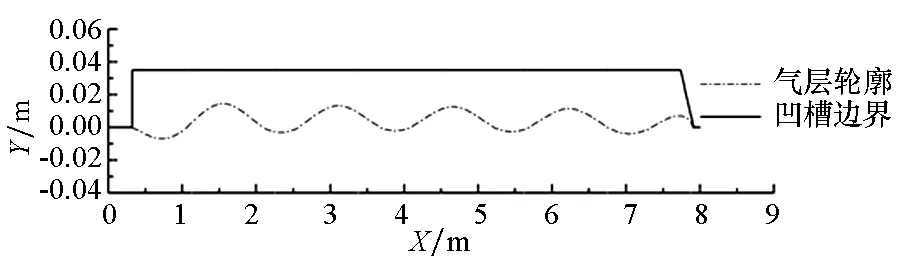
图4　凹槽中的气层波动形态Fig.4　Wave pattern of air layer on bottom hollow

2.2速度对气层波动的影响

图5给出了槽深h=0.46%Lh时不同来流速度下的气层波动形态。由图5可知：来流速度增加，凹槽内气层的波长增大，且第一个波峰位置沿来流向后移动；波高沿来流方向的衰落减小。

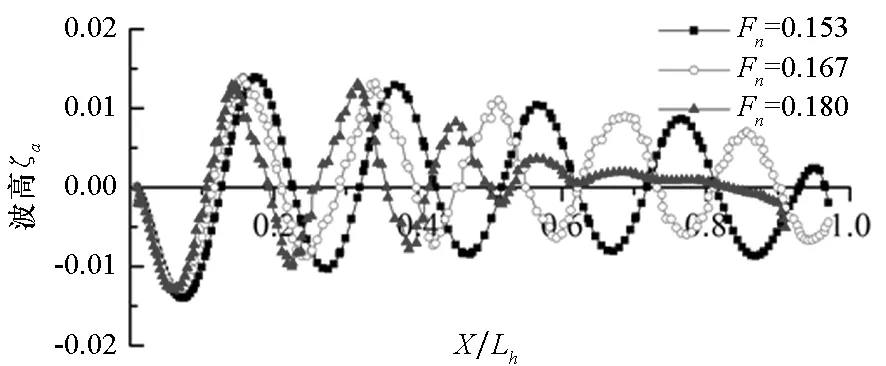
图5　不同速度下气层的典型波动形态Fig.5　Typical air layer shape at different velocity

图6给出了气层波动的第一个波峰至首部断阶的纵向距离Ld随来流速度的变化；图7给出了平均波长λ随来流速度的变化(平均波长λ为除首、尾波动之外的波长平均值)。由图6和图7可知：Ld与λ随来流速度的增加而增大。

图6　第一个波峰与断阶的距离随航速的变化Fig.6　Effect of velocity on the distance of first wave crest to step

图7　气层平均波长随航速的变化Fig.7　Effect of speed on average wave length of air layer

通过线性回归分析可获得λ和Ld随V2的变化关系，回归曲线如图6和图7所示，回归公式如式(10)及式(11)所示。

λ=0.636V2

(10)

Ld-0.126=0.476V2

(11)

根据水面舰船的波动理论可知水面航行体的兴波波长可表示为：

λ=2π·Fn2·L

(12)

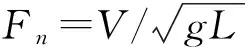
(13)

由上式可知：除凹槽首尾部外，气层波长随速度的变化规律与水面航行体的兴波规律基本一致。在靠近凹槽首部及尾部，由于断阶及尾部斜坡的干扰，气层的波动规律相对复杂。式(11)中的常数项0.126可能与凹槽构型、断阶高度、气流量、吃水等因素有关，尚需进一步研究。

2.3三维波动特征

图8给出了Fn=0.173时凹槽内的气层波形图。由图8可知：波形关于凹槽中纵剖面对称；气层波动在凹槽侧壁的干扰及反射作用下，呈现出明显的相干现象。

图8　Fn=0.173时凹槽中的气层波动形态图Fig.8　Wave pattern of air layers on bottom hollow when Fn=0.173

图9给出了Fn为0.147，0.193，0.207时，凹槽内气层的波形图像。由图9可知：气层的相干波形与来流速度有关；来流速度越大，相干现象越明显；波动从凹槽侧壁反射之后，形成二次叠加。

(a) Fn=0.147

(b) Fn=0.193

(c) Fn=0.207图9　不同速度下凹槽中气层的波动形态图Fig.9　Wave pattern of air layers on bottom hollow at different velocity

图10给出了凹槽内气层形态计算结果与Matveev势流计算结果[17]的对比，从气层的波动相干性及扩散规律上看，二者基本一致。相对于Matveev的势流方法，黏性计算方法的优点在于：该方法不仅可有效模拟凹槽中的气层形态，同时还可以计算气层的非稳态发展过程以及气层从凹槽侧边的溢出情况。

(a) 黏性计算结果(a) Viscosity calculation result

(b) Matveev的势流计算结果(b) Matveev′s potential flow results 图10　凹槽首部的气层波形对比Fig.10　Comparison of wave pattern in front of hollow

图11　Fn=0.173时三维凹槽中纵剖面波形与二维波形的对比Fig.11　Comparison of 3D wave pattern and 2D wave pattern when Fn=0.173

图11和图12给出了不同速度下，中纵剖面上的气层波形与二维波形的对比。图中坐标原点为气层的起始位置，与凹槽首部断阶的下边缘相对应；hw/h为波高与凹槽深度之比，X/Lh表示气层长度与凹槽长度之比。由图11和图12可知：三维凹槽中纵剖面上的气层波形与二维波形不同。由于波的反射与干涉，三维气层波动的平均波高有所降低，并且第一个波峰、波谷出现的位置会向凹槽首部移动；二维波形的波高沿流动方向逐渐降低，但是三维波动由于凹槽侧壁的反射波在凹槽尾部叠加，在凹槽尾部有所增大，导致波高沿流动方向并非单调变化。图13给出了Fn=0.173时气层波动的三维相干图像及中纵剖面上的波高变化曲线。

图12　Fn =0.180时三维凹槽中纵剖面波形与二维波形的对比Fig.12　Comparison of 3D wave pattern and 2D wave pattern when Fn =0.180

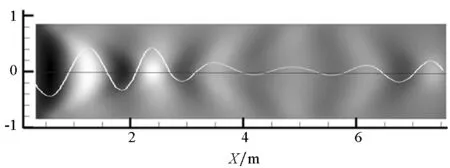
图13　Fn=0.173时凹槽中干扰波系及中纵剖面上的波形图Fig.13　3D coherent waveform in hollow when Fn=0.173

2.4波动相似律

根据式(10)可知，对于几何相似的两种凹槽(设为凹槽1和凹槽2)，稳定气层形成后，波长分别满足关系式：

(14)

(15)

(16)

(17)

若Fn1=Fn2，则有：

(18)

由式(18)可知：在相同傅汝德数下，几何相似凹槽中的气层平均波长满足几何相似性。

利用黏性方法计算几何相似凹槽在3种不同尺度下的气层形态，凹槽长度分别为：7.59 m，15.18 m，30.36 m，对应的缩尺比α为1，2和4。表1给出了气层波动参数的黏性方法计算结果及几何相似律换算的结果。表中α=1时仅给出黏性方法计算结果，α=2与α=4时，同时给出了黏性方法计算结果和换算结果，计算过程中无因次气流量系数Cq相等。

由表1可知：将凹槽尺度放大2倍和4倍后，利用黏性方法计算所得波形的参数与根据几何相似规律换算得到的波形参数基本一致，两者的误差小于1%。

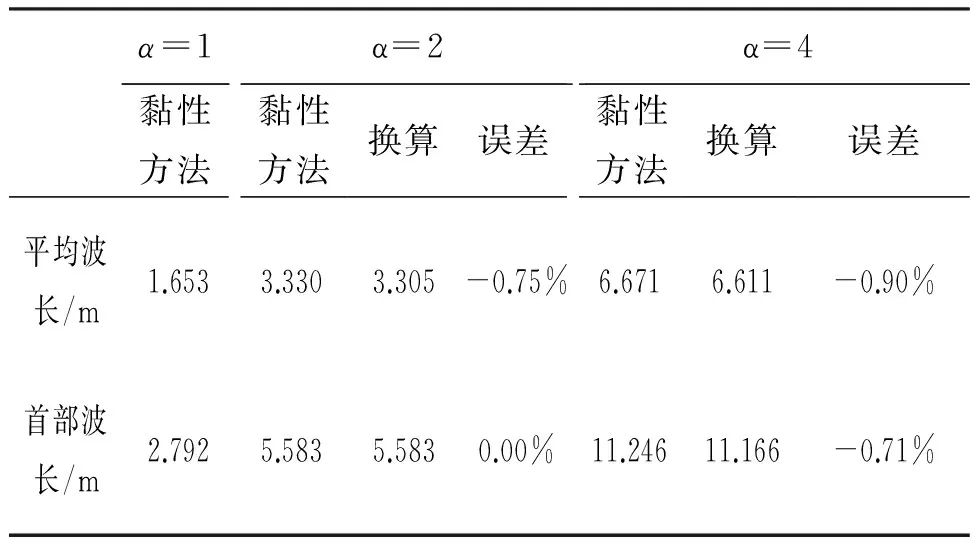
表1　不同凹槽尺度中的波形参数

图14给出了不同尺度下气层的无因次波形。由图14可知：Fn与Cq相等时，几何相似凹槽中的无因次气层波形基本一致，说明波形满足几何相似性。图15给出了相似凹槽中的气层经等比例缩放至同一尺度后的波动图像。为了更加清晰地显示气层形态，凹槽的长度方向均缩小为原来的1/5，深度方向不变。由图15可知：缩放至同一尺度之后，相似凹槽中的气层图像几乎一致，波形参数满足几何相似律。

图14　Fn相等时相似凹槽中的无因次气层形态Fig.14　Non-dimensional wave shape of different scale hollow with the same Fn

图15　缩放至同一尺度后的气层图像对比Fig.15　Air layer shape at different scale ratio

3　结论

1)速度不同，气层波动形态有所不同：随着速度的提高，凹槽内的波长增大，凹槽内的波高沿流动方向衰落减小，且第一个波峰位置向后移动。

2)气层在凹槽中呈现波动形态，速度增加气层波长增大。对于二维凹槽模型，波长约等于速度平方的0.64倍；

3)气层在三维凹槽模型侧壁的干扰及反射下呈现相干波系，从而改变了气层波高及局部厚度；

4)气层波动满足傅汝德相似。Fn与Cq相等时，几何相似凹槽中的无因次气层波形基本一致，即：波形满足几何相似性，波形参数满足几何相似律。

References)

[1]欧勇鹏. 气泡高速艇水动力性能研究[D]. 武汉:海军工程大学, 2009.

OU Yongpeng.Study on the hydrodynamic performance of a high speed boat with high speed boat[D]. Wuhan:Naval University of Engineering, 2009.(in Chinese)

[2]Madavan N K, Deutsch S, Merkle C L. Measurements of local skin friction in a microbubble modified turbulent boundary layer[J]． Journal of Fluid Mechanics, 1985, 156: 237-256.

[3]Dong W C, Ou Y P. Experimental study on resistance and longitudinal motion of high-speed air cavity craft[J]. Journal of Ship Mechanics, 2011, 15(9): 949-959.

[4]Butuzov A A. State of art in investigations and development for the ship on the artificial cavities[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 1999, 7(S1): 1-10.

[5]Gokcay S. Revisiting artificial air cavity concept for high speed craft[J]. Ocean Engineering, 2004, 31: 253-267.

[6]Gcaptain S. Floating on air-dk group receives first order for air cavity system[EB/OL]. (2012-03-05) [2015-05-28]. http://www.gcptain.com/floating-group-receives-order/20120305.html.

[7]Butuzov A A, Vasin A I, Drozdov A L, et al. Full scale trials of a boat with an air cavity[C]//Proceedings of Shipbuilding Problems, 1981, 28: 45-51.

[8]Butuzov A A, Gorbachov Y N, Ivanov A N． Reduction of ship resistance using ventilated gas cavities[J]. Shipbuilding, 1990, 11: 3-64.

[9]Sverchkov A V. Application of air cavities on high-speed ships in Russia[C]//Proceedings of International Conference on Ship Drag Reduction SMOOTH-SHIPS, Istanbul, Turkey, 2010.

[10]Andrey V S. Potential of the artificial air cavity technology for raising the economic efficiency of china′s inland waterway shipping[C]//Proceedings of International Conference on Fast Sea Transportation(FAST2007), Shanghai,China, 2006: 1-7.

[11]Butuzov A A, Sverchkov A, Poustoshny A, et al. High speed ships on the cavity：scientific base, design peculiarities and perspectives for the mediterranean sea[C]//Proceedings of the 5th Symposium on High Speed Marine Vehicles, Capri, Italy, 1999.

[12]Zverkhovskyi O, van Terwisga T, Delfos R, et al. Experimental study on developed air cavities under ahorizontal flat plate[C]//Proceedings of 8th International Symposium on Cavitation(CAV2012), Singapore, 2012.

[13]Zverkhovskyi O. Ship drag reduction by air cavities[D]. Enschede, Netherlands: Gildeprint, 2014.

[14]蔡泽伟, 徐亦凡. 近水面细长体的水动力导数数值计算[J]. 国防科技大学学报, 2000, 22(6): 120-124.

CAI Zewei, XU Yifan. Numerical solution to hydrodynamic derivatives of a slender-body near free surface [J].Journal of National University of Defense Technology, 2000, 22(6): 120-124. (in Chinese)

[15]Butuzov A A. Limiting parameters of an artificial cavity formed on the lower surface of a horizontal wall[J]. Fluid Dynamics, 1966, 1(1): 116-118.

[16]Kim D, Moin P. Direct numerical simulation of air layer drag reduction phenomenon over a backward-facing step[C]//Proceedings of 63rd Annual Meeting of the APS Division of Fluid Dynamics, 2010: 351-363.

Characteristics of air layer fluctuations on flat bottom air cavity ship with groove

WU Hao, OU Yongpeng

(Department of Naval Architecture, Naval University of Engineering, Wuhan 430033, China)

In order to improve the design effectiveness of large flat bottom ship with groove, a calculation method with combination of RANS equations and VOF two-phase-flow model was proposed for a large flat bottom ship with groove. The dynamic development of air layer in the groove was found. Based on the analysis of air layer fluctuations with different flow velocity, the difference of air layer fluctuation characteristics between three-dimensional and two-dimensional was explained and the fluctuation similar law of air layer was obtained. Numerical results show that: fluctuations of air layer appear in the groove and the wavelength of air layer increases with the increasing of velocity; the wavelength is equal to 0.64 times of the square of velocity; air layer presents phenomenon of coherent and reflection at the side walls of groove, so the wave height and the thickness of local air layer are changed; fluctuations of air layer is satisfied with Froude similarity.

flat plate ship; wave pattern; regression analysis; similar law; VOF model

10.11887/j.cn.201604028http://journal.nudt.edu.cn

2015-06-18

工信部高技术船舶科研基金资助项目(2011530)；高性能船舶技术教育部重点实验室开放基金资助项目(2013033102)

吴浩(1987—)，男，湖北武汉人，博士研究生，E-mail：hgwuhao@126.com；欧勇鹏(通信作者)，男，讲师，博士，E-mail：oubad@163.com

U661.32

A

1001-2486(2016)04-179-06