控制速度方向的弹道修正导引方法*

徐秋坪，王中原，常思江

(南京理工大学 能源与动力工程学院， 江苏 南京　210094)



控制速度方向的弹道修正导引方法*

徐秋坪，王中原，常思江

(南京理工大学 能源与动力工程学院， 江苏 南京210094)

由于制导炮弹由身管武器发射，其飞行控制能力和导引信息量有限，故基于预测落点位置偏差量来修正速度方向并在控制时间内连续分配导引指令的思想提出一种新的三维末制导方法。根据非线性弹道方程组的级数解预测弹丸落点位置，得到落点与目标的偏差，并提出两种通过此偏差解算当前速度方向修正量的方法。取剩余飞行时间为修正时间，通过将速度方向修正量分配到整个剩余导引段建立加速度修正公式，从而减小导引指令饱和的可能性。通过连续地预测落点和分配加速度指令来实时地导引飞行。仿真结果表明：该导引方法简单可行，精度高，对控制能力要求较低，且具备较好的制导效果和毁伤效果，可为该体制制导炮弹的应用提供参考依据。

制导炮弹；导引方法；弹道修正；落点预测；剩余飞行时间

为适应现代化战争的需要，将现有制式常规炮弹以较低成本改装成具有一定弹道控制能力的制导炮弹，使其具备效费比高、首发命中率高、能高效攻击静止和低速运动目标等优点，目前已成为许多国家研究的热点课题。导引律设计是制导炮弹导引控制系统设计中的关键技术之一，所选择的导引方法的优劣会直接影响到命中目标的精度和制导炮弹的作战性能。由于制导炮弹成本低、体积小，因此其在飞行控制能力及系统复杂度等方面与导弹有较大差别，并且在射击过程中存在诸多随机扰动的影响，故有必要开展适配制导炮弹在复杂飞行环境下的导引方法研究。国内外已开展了大量关于制导炮弹导引律的相关研究工作，提出了不少导引方案。文献[1]在传统比例导引规律的基础上，对视线角速度施加一个偏置量设计了偏执比例导引律。文献[2]设计了一种三维联合偏置比例制导律，该制导律结合了顺轨、逆轨拦截模式，采用时变偏置角速率和时变比例系数。文献[3-4]基于广义卡尔曼滤波多步估计算法，在经典的比例导引方程中引入了视线角加速度，提出了在末制导段采用指向预测命中点的导引方式，以减小在遭遇点附近法向过载的跳动。比例导引律及其改进形式(如时变增益、引入偏置量等)，这些导引方法设计的主要出发点是减小脱靶量，对初始视线转率的精度要求较高且需要消除初始导引误差。随着现代控制理论的发展，不少学者利用优化控制算法研究了新的导引律[5-9]。文献[10]以舰炮发射带有GPS导航和火箭助推的旋转弹为背景对比研究了两种落角控制导引律(运用最优控制理论建立的广义显示导引律和采用重力补偿比例缩放的终端状态向前积分导引律)。文献[11]基于模型预测静态规划技术，提出了对地面目标的一种3-D带落角约束的非线性次优导引律。文献[12]基于传统滑模控制理论和非奇异终端滑模控制理论，提出了一种对固定目标的三维空间耦合带落角约束的导引律。文献[13]将弹丸线性化模型和预测控制理论相结合建立了一种导引律，以减小落点散布。然而，这类导引律需要明确的几何分析和最优控制理论的支撑，并且建立模型相对复杂，对导引信息输入量的要求较多。考虑制导炮弹由身管武器发射，其飞行控制能力有限、抗干扰能力弱，弹丸导引信息量有限，对弹载计算机性能提出了较高的要求，因而模型简单、有效、精度高，对传感器和执行机构要求低的导引方法更适用于制导炮弹。

本文基于实时预测落点位置偏差来修正速度方向和连续分配导引指令的思想，提出了一种新的三维弹道修正导引(Ballistic Correction Guidance, BCG)方法。根据制导炮弹非线性动力学模型的级数解快速有效地预测弹丸落点，用预测的落点近似代替弹丸的实际落点，以求得预测落点与目标之间的位置偏差量，并根据此偏差量解算当前飞行位置处的速度方向修正量，通过在控制时间内连续分配弹道倾角和弹道偏角修正量的方式建立导引关系。同时，还提出了两种根据位置偏差计算速度方向修正量的不同处理方法。通过数值仿真对该导引方法的可行性和有效性进行了初步验证，分析了该导引方法各组成部分的特点，结果表明基于此落点预测算法的导引方法能在此类制导炮弹上有效地工作，其导引精度高，控制过程平缓，末段控制余量较大，对导引信息要求低，且具备较大的落角，从而为该类制导炮弹的导引控制方案设计提供一定的参考。

1　基于弹道方程组级数解预测落点

预测落点方法有多种，可分成两大类型：数值积分法和函数逼近外推法。数值积分法的实质在于使用数值积分算法对相应的外弹道方程组进行求解，如积分6-D模型、积分3-D模型和积分改进的质点模型等。该方法计算负担较大，耗时较多，解算精度依赖弹载计算机的性能和解算步长，不易实时修正相关系数。函数逼近外推法通过对弹道方程组进行多元函数线性化(或非线性函数)逼近求解，文献[14-15]中将六自由度刚体弹道模型线性化处理，建立了弹道诸元的解析表达式，但这些表达式涉及参数较多且形式复杂，不适宜实际应用。采用本文导引律需实时预测飞行落点，这就要求落点预测算法简单、准确而快速。考虑实际中对诸多弹道参数的测试也难满足刚体弹道的计算需求，因而实际中一般采用质点弹道方程组。以质点弹道方程组的级数解法为基础来预测弹丸落点，计算简洁，快速有效且通用性强。考虑风的3-D质点弹道模型[16-17]描述为：

(1)

其中

(2)

式中：v, vr分别为弹丸地速和风速；m为弹体质量；ρ为大气密度；S为特征面积；g为重力加速度；CD为全弹阻力系数；θ, ψ分别为弹道倾角和偏角；x, y, z分别为弹丸位置在地面坐标系下的投影分量；wx, wz分别为纵风和横风风速。

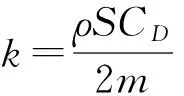
(3)

将各位置变量在当前预测点处关于时间变量t泰勒级数展开并略去二阶导数以上各项，可得如式(4)所示弹道方程级数解析解：

(4)

式中带下标i的参数为当前预测点处的诸弹道参数，可由跟踪雷达或弹载卫星定位装置实时测量提供，此处假设测量信息是准确的，且在弹丸后半段飞行过程中相应参数值不变。则令y=0，可得从预测点到弹丸落地的剩余飞行时间，用弹道倾角和弹道偏角表示可写为：

(5)

将tgo代入式(4)可预测弹丸落点为：

(6)

若已知目标位置(xT,zT)，可预测出弹丸落点与目标之间的位置误差：Δx=x-xT,Δz=z-zT，此位置误差将作为本文导引方法的输入量。

2　弹道修正导引律

弹丸在发射及飞行过程中会受到诸多不确定因素的干扰，如初始扰动，随机风等，都会导致命中精度降低。图1给出了基于上述落点预测方法的弹道修正导引律示意图。图中V，V′分别表示修正前后的速度矢量，二者大小相等方向不同，法向和侧向分别相差角度Δθ,Δψ。无控时，弹丸以V方向沿着轨迹1飞行，不能命中目标。在A点处预测落点得其与目标之间的偏差为(Δx,Δz)。根据弹道修正的思想，在纵向平面内，若落点在目标前方(沿射击方向)则需减小A点处弹道倾角，若落点在目标点后方则需增大其值，但是弹道倾角修正量存在一个较大值和一个较小值，由于应用于末制导且较大的修正值不符合飞行实际情况则需舍去，侧向平面内弹道偏角的修正量也存在相同特点。因此，根据偏差(Δx,Δz)可解算出相应唯一的速度方向修正量(Δθ,Δψ)。根据(Δθ,Δψ)以某种方法求得相应法向和侧向的加速度修正量aθ和aψ，则弹丸以修正后的加速度沿V′方向(轨迹2)飞行并命中目标。

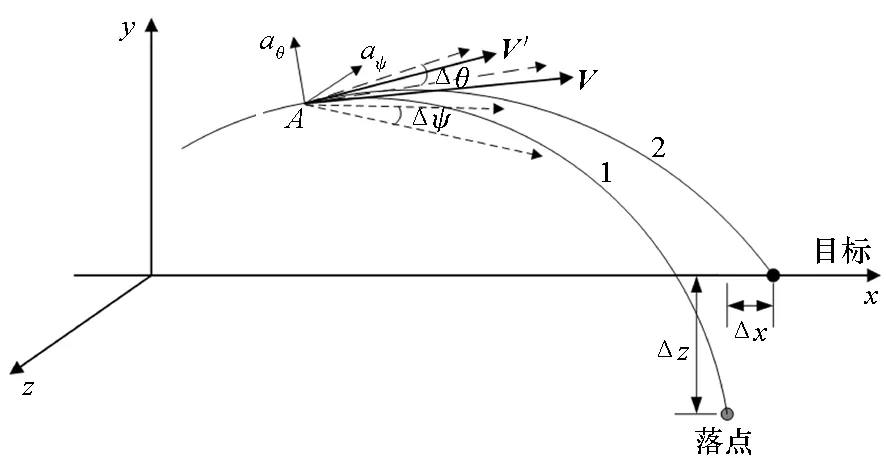
图1　弹道修正导引律示意图Fig.1　Diagram for ballistic correction guidance

实际飞行中将V改变(Δθ,Δψ)到V′方向是不可能瞬时完成的，需在一定修正时间Δt内完成该任务。因此，可建立如式(7)所示形式的加速度修正量：

(7)

图2　纵向平面修正量单步离散示意图Fig.2　Single-step discrete diagram of corrections in vertical plane

式中：K为导引系数。Δt的值越大则导引指令值越小，飞行轨迹修正越缓慢。Δt的值可取为剩余飞行时间tgo，意味着将Δθ和Δψ的改变量分配到剩余的整个导引段中执行，而每一步只需要执行一个较小的修正量。图2给出了纵向平面内分摊导引的单步离散过程。第i步预测落点Pi位于目标T的后方(沿射击方向)，相应的理想修正角度为Δθi，通过分配后实际改变的角度为Δθ′i，沿着相应导引指令飞行至第i+1步，预测落点为Pi+1，根据上述弹道修正思想，Pi+1比Pi更接近目标点，即有Δxi+1<Δxi，此时理想弹道倾角修正量Δθi+1就越小，即Δθi+1<Δθi，再次分配，第i+1步弹道倾角的实际修正量为Δθ′i+1，沿着相应导引指令飞行预测的落点Pi+2就越趋于目标。这样通过连续的预测和分配导引指令，Δθi逐渐减小，相应射击偏差量也逐渐趋于零。

考虑制导炮弹控制能力有限，每次分配的导引指令不宜过小或过大，过小则会导致修正能力不足，过大则会使得导引指令饱和，这就需要选择合适的K和Δt，以降低导引指令饱和的可能性。设acmax为导引指令的最大控制能力，则加速度修正指令可写为：

(8)

如何根据预测的偏差量(Δx,Δz)解算当前状态下(Δθ,Δψ)是建立本文导引律的关键所在，这里提出了两种解算方法。

方法A：利用弹道方程组的级数解建立(Δx,Δz)与(Δθ,Δψ)的非线性耦合关系。

根据上述落点预测算法，以当前(θi,ψi)预测落点位置为(x,z)。式(6)可写为：

(9)

预测落点偏离目标Δx=x-xT,Δz=z-zT。假设当前(θi,ψi)改变为(θi+Δθ,ψi+Δψ)并预测其落点为(x′,z′)，则落点位置改变量为Δx′=x′-x,Δz′=z′-z。若此时的(Δx′,Δz′)恰巧等于(或在一定精度下近似等于)(-Δx, -Δz)，则有x′=xT,z′=zT。

记θ′=θi+Δθ,ψ′=ψi+Δψ。根据式(9)可建立二元非线性方程组为：

(10)

此二元常系数非线性方程组只有θ′i,ψ′i为未知量，其余参数均为该预测落点处相应参数。若解得θ′i,ψ′i，则Δθ=θ′i-θi,Δψ=ψ′i-ψi。记方程组(10)中右边为f1(x1,x2)和f2(x1,x2)，其中x1=θ′i,x2=ψ′i，则方程组(10)的解可等价为如式(11)所示方程组的解：

(11)

根据前面的分析，此方程组有解且唯一。对于此非线性方程组的求解问题，本文将其转化为解非线性最小二乘问题，即与之等价的目标函数

(12)

的极小值问题，搜索方向采用Gauss-Newton法，可减小计算复杂程度，且收敛速度快，计算精度高[18-19]。

方法B：采用线性化近似处理方法建立(Δx,Δz)与(Δθ,Δψ)的耦合关系。

设F为某质点弹道方程组的解函数，根据外弹道理论，纵向和侧向射程[20]可写为：

(13)

假定只在ti处改变(Δθi,Δψi)来影响(Δx,Δz)，则线性化(X,Z)有：

(14)

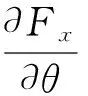
假定在当前位置处引入两组微小变化量(Δθ1,Δψ1)和(Δθ2,Δψ2)，分别预测相应的落点偏差量为(Δx1,Δz1)和(Δx2,Δz2)。根据式(14)可建立方程组：

(15)

解出

(16)

则方程组(14)可解为

(17)

进一步反解可求得ti时刻速度方向角的理想修正量(Δθi,Δψi)，如式(18)所示。

(18)

上述两种求解方法既考虑了纵向和侧向的耦合关系，又能根据当前飞行环境实时地建立(Δθ,Δψ)和(Δx,Δz)的关系。根据上述讨论可建立弹道修正导引方案，其流程如图3所示。

图3　弹道修正导引方案流程图Fig.3　Flow diagram of BCG strategy

3　算例仿真与分析

在MATLAB环境下对某制导炮弹采用此预测算法和弹道修正导引方法进行数值仿真，并对此导引方法的可行性和有效性进行评估。仿真条件：弹重m0=33.305 kg，弹径130 mm，初速v0=930 m/s，发射角θ0=45°,ψ0=0°。发射坐标[-27 734, 0, 0]m，目标坐标[0, 0, 0]m。忽略科氏力。假设测量信息是准确的，加速度修正量由鸭舵控制机构提供，其最大修正能力acmax=±1 g，控制系统理想工作。发射及飞行过程中主要扰动源如表1所示。

表1　主要弹道扰动源

预测精度受到起始预测高度及相应飞行状态参数的影响。取一组上述扰动源进行仿真，在高度为7 km到50 m的飞行段预测落点，其预测误差如图4所示。图中δx,δz分别为预测落点与其实际落点的纵向和横向之差。离目标越远进行预测，剩余飞行时间越长且预测误差越大；随着弹丸越接近目标预测误差呈快速收敛趋势，预测误差的相对误差在1.7%以内且也呈逐渐减小的趋势。当高度到达1 km后纵向和横向预测误差均缩小到1 m的范围内，均可视为满足精度要求。

(a) 纵向预测误差(a) Prediction error of down-range

(b) 横向预测误差(b) Prediction error of cross-range图4　落点预测偏差Fig.4　Impact point prediction error

为了验证本文导引方法的可行性和有效性，考虑上述随机扰动，将不采用末制导和采用上述导引方法末制导的结果进行对比分析。取3000组上述随机扰动源进行Monte Carlo模拟打靶，不采用末制导时弹丸落点的纵向和横向误差最大达到700 m，其圆概率偏差CEP=315.14 m，射击精度低。在上述模拟打靶中选取10组随机扰动，采用本文导引方法进行末制导，导引起始高度为5 km，导引系数选为K=2，采用方法A解算加速度指令，飞行轨迹如图5所示。为避免接近目标时加速度指令过大，当高度y≤50 m后就停止末制导而采用自由飞行，后面采用比例导引律对比分析时也做相同处理。可以看出，存在扰动时，尤其当扰动较大时，如图中编号为1的随机扰动，弹丸无控飞行的射击偏差为(-530.70, 578.08)m，无法命中目标，采用本文末制导方法其落点偏差仅(-1.75×10-2, 3.73×10-2)m，且在其余扰动下均能有效地命中目标。

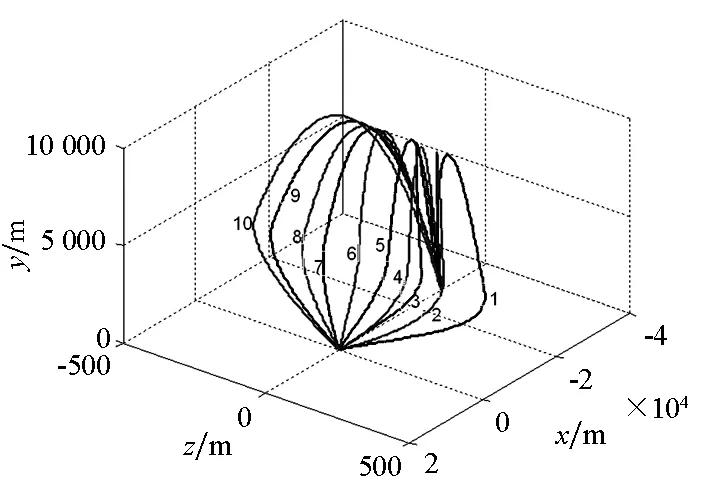
图5　10组随机扰动下导引飞行轨迹Fig.5　Guided trajectories under 10 stochastic perturbations

(a) 纵向加速度指令曲线(a) Histories of the pitch acceleration commands

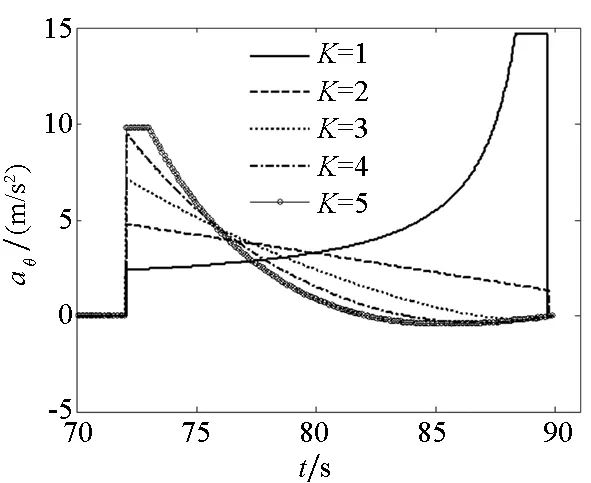
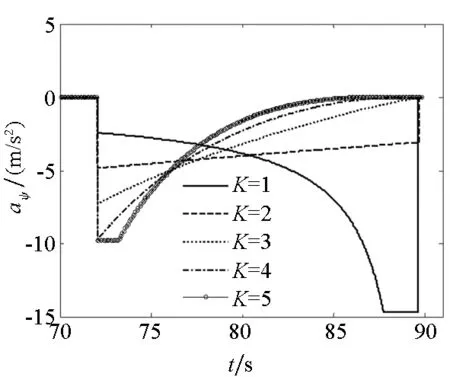
在上述编号为1的扰动下，采用不同导引系数进行末制导，相应加速度修正量变化情况如图6所示，射击误差对比如表2所示。可以看出，当K=1时每次加速度分摊量过小导致修正能力不足，且加速度指令呈逐渐增大的趋势，甚至超过其修正范围，射击精度较低，因此需要K大于1。随着K的增大，导引指令初始值增大，但随着飞行时间的增加导引指令呈快速收敛趋势，最终趋于零。这意味着导引过程中加速度修正量的控制余量逐渐增大，其末段机动性能较强；但K的值过大会导致导引指令饱和(如K=5)，并且整个控制过程加速度修正量的变化范围也较大。从精度上讲，K≥2时命中精度已相当高，可视为直击命中目标。考虑制导精度、导引指令的变化范围及其变化过程的平稳度，导引系数可选在2～3之间。

(b) 侧向加速度指令曲线(b) Histories of the yaw acceleration commands图6　不同导引系数下导引指令变化曲线Fig.6　Guidance command profile under different gains

K=1K=2K=3K=4K=5纵向误差/m-18.34-1.75×10-24.46×10-42.92×10-4-8.28×10-5侧向误差/m31.953.73×10-21.20×10-4-5.31×10-51.94×10-5

(a) 纵向加速度指令曲线(a) Histories of the pitch acceleration commands

(b) 侧向加速度指令曲线(b) Histories of the yaw acceleration commands图7　不同末制导高度处导引指令变化曲线Fig.7　Guidance command profile under different initially guided altitudes

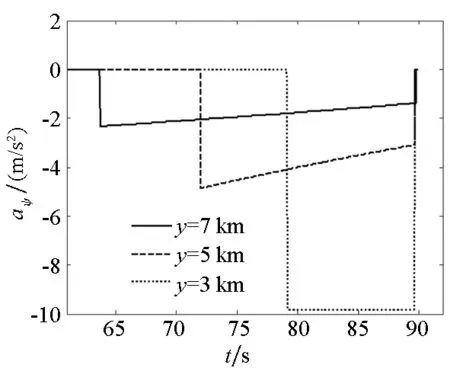
在编号为1的扰动下，取K=2在不同高度下进行末制导，相应加速度指令变化情况如图7所示。末制导起始高度影响着修正时间Δt的值。在整个导引过程中Δt的值随着高度不断地变化，越接近目标其值越小。考虑落点预测误差以及制导炮弹控制能力有限，若起始导引高度越接近目标则轨迹修正时间越短，单步分配的指令就越大，甚至会超过其修正范围，并且可能导致导引指令处于持续饱和状态(如末制导初始高度为3 km时的侧向导引指令)，其命中精度也越低；若导引起始位置离目标越远则预测精度相对较差且轨迹修正越缓慢，故末制导起始高度可选在5 km左右。

在不同高度、导引系数和随机扰动下，对方法A和方法B解算导引指令进行对比仿真，如图8～10所示。结果发现：采用方法B的计算量比方法A小，二者的射击精度几乎一样，均能有效地命中目标，相应加速度修正量也很相近。但采用方法B解算的末段导引指令略有增大的趋势，同时其纵向加速度指令在导引初始段存在微小段畸变现象。由于ψ0=0°，即使存在扰动时其值也很小，同时弹道偏角和由其引起的侧向偏差相对于弹道倾角及其引起的纵向偏差而言均非常小，根据两次微小扰动分别预测落点的偏差而建立起(Δθ,Δψ)与(Δx,Δz)之间的关系，考虑了法向和侧向的耦合，导致线性近似解算(Δθ,Δψ)时纵向加速度修正量存在波动现象。当ψ0和θ0相差不大时可避免加速度指令振荡现象，如将ψ0设定大于15°而θ0不变时加速度指令无振荡现象。若采用方法A则不存在这一现象，整个控制过程变化平缓且无振荡，虽然两种方法精度相差不大，但从射击要求和控制稳定出发采取方法A处理为佳。本文与比例导引末制导比较时均采用方法A处理。

(a) 纵向加速度指令比较(a) Comparison of the pitch acceleration commands

(b) 侧向加速度指令比较(b) Comparison of the yaw acceleration commands图8　不同导引系数下方法A和方法B导引指令对比Fig.8　Guidance command comparision between method A and method B under different gains

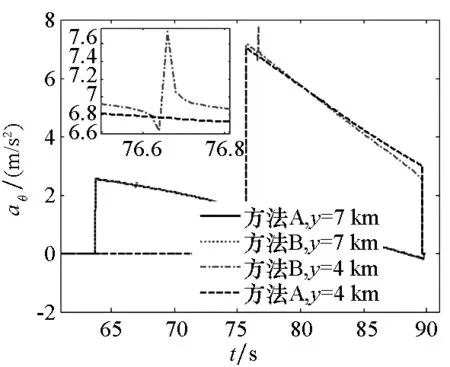
(a) 纵向加速度指令比较(a) Comparison of the pitch acceleration commands

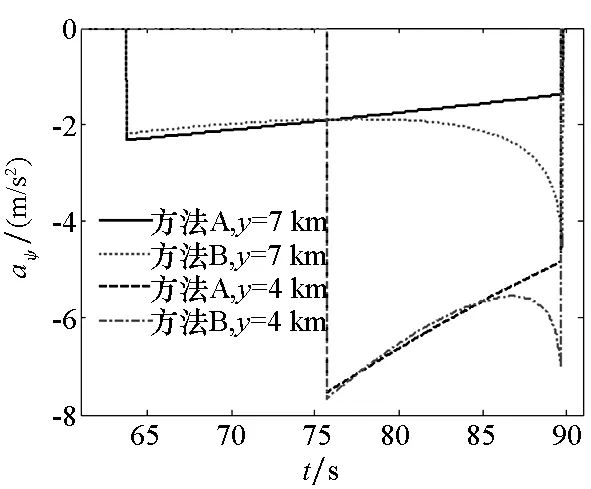
(b) 侧向加速度指令比较(b) Comparison of the yaw acceleration commands图9　不同末制导高度下方法A和方法B导引指令对比Fig.9　Guidance command comparision between method A and method B under different initially guided altitudes

(a) 纵向加速度指令比较(a) Comparison of the pitch acceleration commands

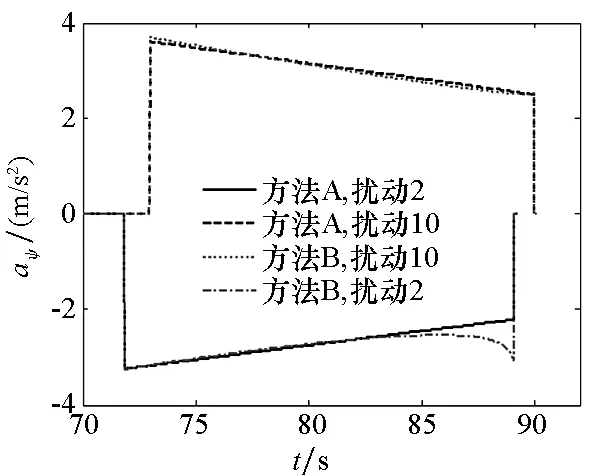
(b) 侧向加速度指令比较(b) Comparison of the yaw acceleration commands图10　不同扰动下方法A和方法B导引指令对比Fig.10　Guidance command comparision between method A and method B under different perturbations

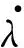
(19)

式中：rx, ry, rz为弹目距离矢量在地面系下的各分量。将视线角速率转到速度坐标系下有：

(20)

则三维比例导引律加速度指令[21-22]为：

(21)

式中：N为比例导引系数，V为弹丸飞行速度。

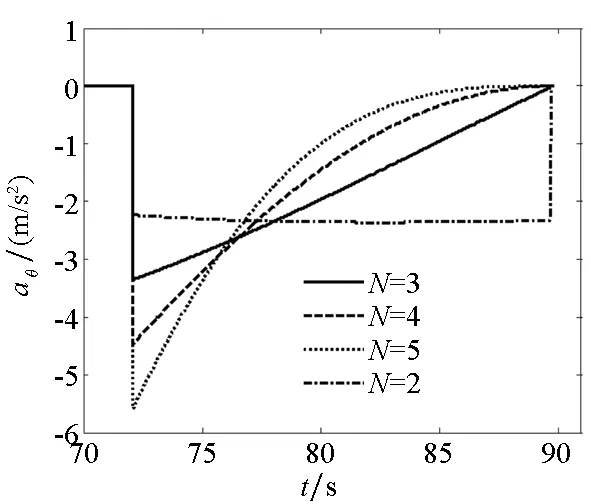
在上述编号为1的随机扰动下采用PNG末制导，结果如图11所示。取N为3，对比仿真PNG和BCG两种末制导，如图12、图13所示。采用BCG末制导的射击精度相对较好，且其轨迹修正更加平缓，尤其在导引初始段，从轨迹的弯曲程度可看出BCG对控制能力的要求更低。从图12可以看出，用PNG末制导的弹道倾角和弹道偏角初始段突变较大而后趋于某个值，中间段其值的变化速率较大；而采用BCG末制导的弹道倾角和弹道偏角初始段突变较小，整个飞行过程中其值变化很平稳且呈逐渐增加的趋势，同时可获得更大的落角，这说明经过连续分配导引指令后BCG可取得更好的导引效果。

(a) 纵向加速度指令曲线(a) Histories of the pitch acceleration commands

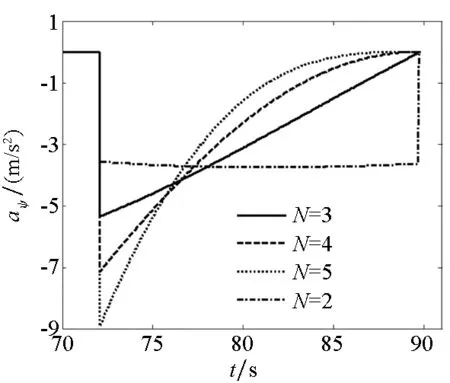
(b) 侧向加速度指令曲线(b) Histories of the yaw acceleration commands图11　不同导引系数下PNG末制导指令变化曲线Fig.11　Command histories of PNG under different N

(a) 弹道倾角曲线(a) Pitch angle profile

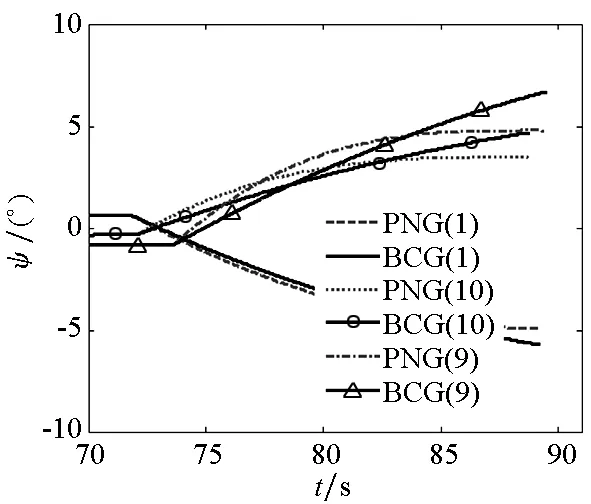
(b) 弹道偏角曲线(b) Yaw angle profile图12　不同扰动下BCG和PNG末制导的速度方向角变化曲线(取图5中扰动的编号为1,9,10)Fig.12　Attitude angle profile for comparing BCG and PNG under different perturbations from fig.5 (1, 9, 10)

(a) 纵向轨迹(a) Vertical trajectories

(b) 侧向轨迹(b) Lateral trajectories图13　BCG和PNG末制导弹道曲线对比Fig.13　Trajectory profile comparision between BCG and PNG

4　结论

1)基于弹道方程组级数解的弹丸飞行落点预测模型提出了一种连续修正速度方向的末制导方法，该导引律通过适当分配加速度指令以减少导引指令饱和的可能性。

2)在考虑随机扰动和控制能力受限的条件下对所提导引方法进行了仿真分析，验证了该导引方法的可行性和有效性，分析了导引律中各参数对制导效果的影响并给出了相应参数的选取条件(导引系数取在2～3之间，末制导起始高度取在5 km左右为佳)，这些参数都影响着导引指令每次分配量的大小。

3)对比分析了根据落点处弹目偏差量解算速度方向修正量的两种方法，采用方法B求解的加速度修正量会出现畸变现象且需满足弹道倾角和弹道偏角相差不大的要求，但是其计算量较小，解算速度较快，更适用于低等级弹载计算机；而采用方法A的求解量较大但精度更高，控制效果更好。

4)与比例导引法相比，采用BCG末制导的射击精度相对较高，对控制能力的要求较低，具备更好的制导效果和毁伤效果。

5)该导引方法简单可行且有效，可与其他落点预测算法相结合，可为制导炮弹导引律的设计提供一定的参考。

References)

[1]王辉, 章虹虹. 高精度偏置比例导引末制导律研究[J]. 航天控制, 2009, 27(6): 19-22.

WANG Hui, ZHANG Honghong. The development of high-precision biased proportional navigation terminal guidance control[J]. Aerospace Control, 2009, 27(6): 19-22.(in Chinese)

[2]闫梁, 赵继广, 沈怀荣, 等. 带末端碰撞角约束的三维联合偏置比例制导律设计[J]. 航空学报, 2014, 35(7):1999-2010.

YAN Liang, ZHAO Jiguang, SHEN Huairong, et al.Three-dimensional united biased proportional navigation guidance law for interception of targets with angular constraints[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(7): 1999-2010. (in Chinese)

[3]金学英. 基于多点估计的比例导引法的改进[D]. 沈阳:沈阳航空航天大学, 2009.

JIN Xueying.The improving of proportional navigation law based on multi-step estimating[D]. Shenyang: Shenyang Institute of Aeronautical Engineering, 2009. (in Chinese)

[4]赵文成, 金学英, 那岚. 末制导段比例导引法的改进[J]. 指挥控制与仿真, 2009, 31(4): 97-99.

ZHAO Wencheng, JIN Xueying, NA Lan.Modifying of proportional guidance law at terminal guidance[J]. Command Control & Simulation, 2009, 31(4): 97-99.(in Chinese)

[5]Maity A, Oza H B, Padhi R.Generalized model predictive static programming and angle-constrained guidance of air-to-ground missiles [J]. Journal of Guidance, Control and Dynamics, 2014, 37(6): 1897-1913.

[6]Lee C H, Kim T H, Tahk M J. Interception angle control guidance using proportional navigation with error feedback [J]. Journal of Guidance, Control and Dynamics, 2013, 36(5): 1556-1561.

[7]Kumar S R, Rao S, Ghose D. Nonsingular terminal sliding mode guidance with impact angle constraints[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(4): 1114-1130.

[8]Alkaher D, Moshaivo A. Guidance laws based on optimal feedback linearization pseudocontrol with time-to-go estimation[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(4): 1298-1305.

[9]Hablani H B. Endgame guidance and relative navigation of strategic interceptors with delays [J]. Journal of Guidance, Control, and Dynamics, 2006, 29(1): 82-94.

[10]Pamadi K B, Ohlmeyer E J. Evaluation of two guidance laws for controlling the impact flight path angle of a naval gun launched spinning projectile [C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit, 2006: AIAA 2006-6081.

[11]Oza H B, Padhi R. Impact-angle-constrained suboptimal model predictive static programming guidance of air-to-ground missiles [J]. Journal of Guidance, Control, and Dynamics, 2012, 35(1): 153-164.

[12]Kumar S R, Ghose D. Three dimensional impact angle constrained guidance law using sliding mode control [C]//Proceedings of American Control Conference, 2014: 2474-2479.

[13]Ollerenshaw D, Costello M. Model predictive control of a direct fire projectile equipped with canards [J]. Journal of Dynamic Systems, Measurement, and Control, 2008, 130(6): 061010-061020.

[14]Hainz L, Costello M. In flight projectile impact point prediction[C]//Proceedings of AIAA Atmospheric Flight Mechanics Conference and Exhibit, Providence, Rhode Island, 2004: 1-40.

[15]Hainz L C, Costello M.Modified projectile linear theory for rapid trajectory prediction [J]. Journal of Guidance, Control, and Dynamics, 2005, 28(5): 1006-1014.

[16]McCoy R L. Modern exterior ballistics: the launch and flight dynamics of symmetric projectiles [M]. Atglen, PA,USA: Schiffer Publishing Ltd., 1999: 165-186.

[17]韩子鹏. 弹箭外弹道学[M]. 北京：北京理工大学出版社, 2008: 84-143.

HAN Zipeng. Exterior ballistics for projectiles[M]. Beijing: Beijing Institute of Technology Press, 2008: 84-143. (in Chinese)

[18]Ortega J M, Rheinbolbt W C.多元非线性方程组迭代解法[M]. 朱季纳, 译. 北京： 科学出版社, 1983: 20-26.

Ortega J M, Rheinbolbt W C. Iterative solution of nonlinear equations in several variables[M]. Translated by ZHU Jina. Beijing: Science Press, 1983: 20-26. (in Chinese)

[19]王德人. 非线性方程组解法与最优化方法[M]. 北京：人民教育出版社, 1979: 238-258.

WANG Deren. Solution of nonlinear equations and optimization methods[M]. Beijing: People′s Education Press, 1979: 238-258. (in Chinese)

[20]王中原. 弹道修正中的控制算法[J]. 弹道学报, 2011, 23(2): 19-21.WANG Zhongyuan. Control method for trajectory correction[J]. Journal of Ballistics, 2011, 23(2): 19-21. (in Chinese)

[21]钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京：北京理工大学出版社, 2008: 90-111.

QIAN Xingfang, LIN Ruixiong, ZHAO Yanan. Missile flight dynamics[M]. Beijing: Beijing Institute of Technology Press, 2008: 90-111. (in Chinese)

[22]Paul Z. Tactical and strategic missile guidance[M]. Washington,USA: American Institute of Aeronautics and Astronautics, 2002: 26-43.

Ballistic correction guidance law based on the control of velocity direction

XU Qiuping, WANG Zhongyuan, CHANG Sijiang

(School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Taking the limited control authority and guidance information of a gun-launched guided projectile into account, a novel three-dimension terminal guidance law based on the combination of the correction of the velocity direction via impact point prediction and continuous distribution of acceleration command was proposed. The deviations between the impact point of the projectile and the target were predicted on the basis of the series solutions of the nonlinear ballistic equations. According to the deviations, two methods to calculate the direction angle corrections of the current speed were addressed. The remaining flight time was designed as the correction time. The acceleration correction formulas were established through sharing the direction angle corrections of the current speed into the whole remaining guided flight to reduce the possibility of command saturation. By predicting the impact point and distributing the acceleration corrections continuously, the trajectory was shaped in real time. The simulation results show that the proposed guidance law is feasible and effective, and provides the performances of high precision with little requirements of control authority, and has great guidance and damage effects, which can provide reference for the application of the guided projectile.

guided projectile; guidance law; trajectory correction; impact point prediction; remaining flight time

10.11887/j.cn.201604023http://journal.nudt.edu.cn

2015-04-15

国家自然科学基金资助项目(11402117)；中国博士后基金资助项目(2013M541676)

徐秋坪(1990—)，男，重庆开县人，博士研究生，E-mail：qiupxu@163.com；王中原(通信作者)，男，教授，博士，博士生导师，E-mail：zywang@njust.edu.cn

TJ765.3

A

1001-2486(2016)04-143-10