轮式移动仿人护理机器人运动稳定性分析

贠今天　邓利浩　桑宏强

1.天津市现代机电装备技术重点实验室,天津,300387　2.天津工业大学,天津,300387



轮式移动仿人护理机器人运动稳定性分析

贠今天1,2邓利浩1,2桑宏强1,2

1.天津市现代机电装备技术重点实验室,天津,3003872.天津工业大学,天津,300387

针对护理机器人腰臂配合抱起病人时容易发生倾翻和侧滑的问题，以自主研发的全方位移动仿人护理机器人为研究对象，从静态和动态两个方面研究机器人此阶段的运动稳定性。在没有负载或低速运动工况下，利用重心投影法，分析其静态稳定性；在有负载变化情况下，利用零力矩点理论并结合递归牛顿-欧拉算法，分析其动态稳定性。最后运用ADAMS仿真软件对护理机器人运动过程进行仿真分析，为确保护理机器人的运动稳定性提供理论依据。

护理机器人；运动稳定性；重心投影法；零力矩点；递归牛顿-欧拉算法

0　引言

近年来随着环境的不断恶化，疫情爆发的概率及规模明显增大。应对疫情过程中，医护人员需要接触感染了传染疾病的患者，易受感染[1]。社会老龄化和高龄化程度不断加深，根据国家统计局《2014年国民经济和社会发展统计公报》，2014年中国13.67亿人口中，60岁及以上的老人2.12亿人，占总人口比例为15.5%，由此带来的护理任务越来越繁重，因此代替或辅助医护人员对病人进行护理的机器人成为目前机器人研究的热点[2-3]。另外，在护理工作中，病人的转移是一个最耗体力的任务，尤其在医护人员短缺的情况下形势更加严峻。为加强医务人员的防护和弥补护理人员的短缺，科研人员针对护理机器人辅助医护人员对病人进行护理这一课题做了大量的研究工作，并取得了一定成果。国内的研究中，沈阳自动化研究所对研发的三点支撑的轮式仿人机器人采用零力矩点(zero moment point,ZMP)理论分析稳定性，但其分析只考虑了零负载工况[4-5]；澳门大学机器人实验室对轮式移动仿人机器人作了稳定性研究，但只是侧重于静态稳定性分析[6]。这些研究都没有分析机器人与病人接触过程中的稳定性。国外的研究中，横滨大学通过在足底安装传感器测得机器人受到的来自接触面的反作用力，从而获得ZMP位置信息[7]，但该方法并不适用于麦克纳姆轮；日本RTC实验室研发了能够抱起病人的RIBA 机器人，并作了碰撞稳定性相关研究[8-9]。然而当前对护理机器人进行运动稳定性分析时，很少考虑与病人接触前后外载荷变化的影响，采用的稳定性判据较为单一，不能真实反映护理机器人运动稳定情况。

护理机器人抱起病人的整个运动过程中，最不稳定的阶段就是护理机器人在移动平台静止时腰臂配合抱起/放下病人，此阶段很容易发生倾翻危险。本文主要针对这一阶段，分析护理机器人在有无负载不同工况下的运动稳定性，并提出相关稳定性判定依据。

1　护理机器人的机械结构特点

护理机器人工作面向对象是人，故不同于一般的工业机器人，其最大的特点在于人机接口的柔顺性和工作安全稳定性，护理机器人要求运行平稳、回转半径小，有足够的力将目标抱起或托起，适应家庭和病房等非结构护理环境。

为满足上述要求，我们设计了全方位移动仿人护理机器人，此机器人高1.35 m，由麦克纳姆轮(4个)、移动平台、腰部、躯干、双臂、灵巧手等部分组成，其机械结构如图1所示。护理机器人是一个多自由度、非线性复杂刚柔混合多体系统，共有15个自由度，包括整体纵向移动、横向移动和回转3个自由度、腰部1个俯仰自由度，头颈部1个回转自由度，每条手臂有5个自由度(包括肩部2个自由度、肘部1个自由度、腕部2个自由度)。

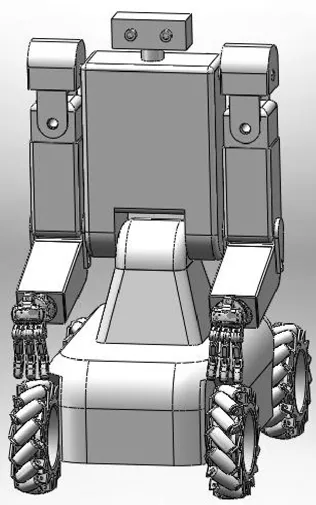
图1　机器人结构简图

护理机器人双臂与移动基座的配合，可极大拓展其操作范围。宽大的机械臂结构与病人有较大的接触面积，能平稳地抱起病人并将其放入轮椅或实现病人在病床与病床之间的平稳转移，防止病人皮肤二次损伤和身体跌落的危险。采用麦克纳姆轮的移动平台具有全向移动能力，非常适合在病房转运空间有限、病床与病床之间通道狭窄的环境工作，具有非常灵活的运动能力及很强的适应性，在提高病人转移效率、增加病房有限空间利用率以及降低医护成本等方面具有明显的效果。

2　护理机器人稳定性分析

全方位移动仿人护理机器人在非结构复杂环境下工作，需要考虑多种不确定性因素，如各构件间的关节摩擦干扰、运动路况、外载荷变化、惯性力、外界环境干扰等，这些因素都影响着护理机器人的运动稳定性。然而当前在对护理机器人进行运动稳定性分析时，面对不同的运动工况，对影响其稳定性的因素考虑得不够全面，采用的稳定性判据较为单一，得到的结果一般较为片面，与实际情况有较大的出入。因此，在对护理机器人的运动稳定性进行分析时，要全面综合考虑影响其稳定性的因素，根据不同的工况采用相应的一种或多种方法相结合的稳定性判据，从而尽可能地获得贴近实际情况的结果。本文重点对护理机器人的静态和动态稳定性两方面进行分析研究，根据不同的工况提出相应的稳定性判据。

针对护理机器人在移动平台静止时腰臂配合抱取目标物(如老年人或病人)这一任务阶段，为方便护理机器人的运动学和动力学分析，可以考虑简化模型，忽略相对作用和惯量较小的头颈部和腕部关节，利用D-H法运动学建模[10]，以移动平台中心为坐标系的原点，建立机器人D-H坐标系，如图2所示。由图2可以看出其复杂的树形结构，左右严格对称，以右臂为例，其连杆参数如表1所示。其中，ai(i=1，2，3，4)为沿着xi-1轴从zi-1轴到zi轴的距离；αi为绕着xi-1轴从zi-1轴到zi轴的距离的角度；di为沿着zi轴从xi-1轴到xi轴的距离；θi为绕着zi轴从xi-1轴到xi轴的角度；q1代表腰部关节;q2代表右臂肩部旋转关节;q3代表右臂肩部摆动关节;q4代表右臂肘部关节; HL代表右臂腕部关节。

图2　机器人D-H坐标系

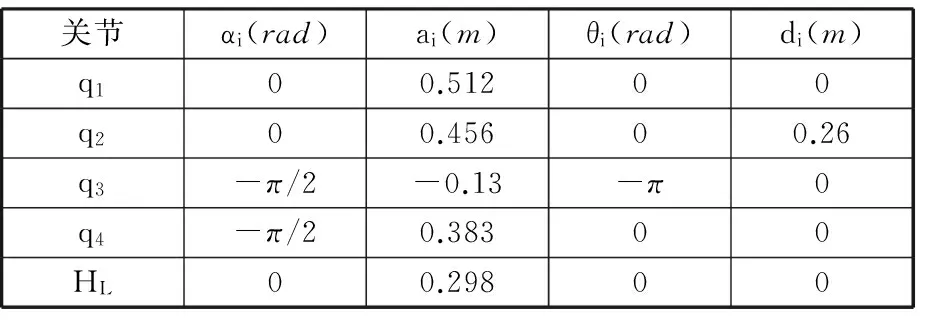
关节αi(rad)ai(m)θi(rad)di(m)q100.51200q200.45600.26q3-π/2-0.13-π0q4-π/20.38300HL00.29800

2.1零负载工况下护理机器人稳定性分析

本文研究的护理机器人工况设定在路面相对平整的医院环境下，由于工作对象为病人，为防止对病人产生二次伤害，要求护理机器人各关节运动平缓稳定。护理机器人在零负载和低速状态下，其动态稳定性问题可以看成各个时刻的静态稳定性问题。稳定的支撑是获得理想运动的重要条件，当机器人系统的重心在水平方向投影位于稳定区域内时，机器人即处于稳定状态，稳定区域即机器人各轮与地面的接触点构成的凸多边形在水平方向上的投影。机器人的质心(xc,yc,zc)的各分量为：

(1)

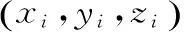
将设计的护理机器人三维模型采用 Parasolid 文件格式导入ADAMS虚拟仿真软件，末端不施加作用力，定义刚体属性、添加约束，然后对其进行运动仿真分析。

各关节驱动STEP函数如下：

腰部关节：STEP(time,0,0d,8,40d)+STEP(Time,8,0d,18,-40d)+STEP(time,18,0d,28,40d)+STEP(time,28,0d,36,-40d)；

右肩关节：STEP(time,0,0d,6,-70d)+STEP(time,6,0d,10,0d)+STEP(time,10,0d,18,30d)+STEP(tIme,18,0d,28,-30d)+STEP(time,30,0d,36,70d)；

左肩关节：STEP(time,0,0d,8,50d)+STEP(time,8,0d,10,0d)+STEP(time,10,0d,18,-30d)+STEP(time,18,0d,28,30d )+STEP(time,28,0d,36,-50d)；右摆件关节：STEP(time,0,0d,8,-8d)+STEP(time,8,0d,28,0d)+STEP(time,28,0d,36,8d)；

左摆件关节：STEP(time,0,0d,60,0d)；

右肘部关节：STEP(time,0,0d,8,-20d)+STEP(time,8,0d,18,5d)+STEP(time,18,0d,28,-5d)+STEP(time,28,0d,36,15d)；

左肘部关节：STEP(time,0,0d,8,13d)+STEP(time,8,0d,28,0d)+STEP(time,28,0d,36,-16d)；

运动仿真时间36 s，步长0.06 s，仿真过程如图3所示。

在护理机器人接触病人之前，其机械臂末端没有负载，各构件运动平缓，图4和图5分别为各构件质心在Z轴和Y轴方向上的轨迹，根据重心投影法稳定判据，将质心轨迹代入式(1)可得到护理机器人机械系统整体重心的轨迹，由图6和图7可以看出机械系统整体重心轨迹在Z轴、Y轴方向上的值一直在机器人各轮与地面的接触点构成的稳定区域(长680 mm,宽510 mm的矩形)内，故护理机器人处于静态稳定状态。

图3　护理机器人仿真流程图

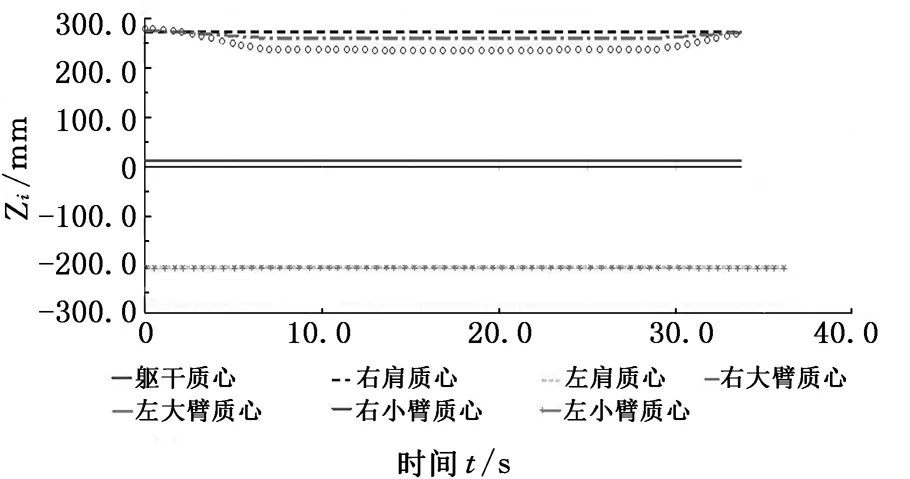
图4　各构件质心在z轴方向上的轨迹

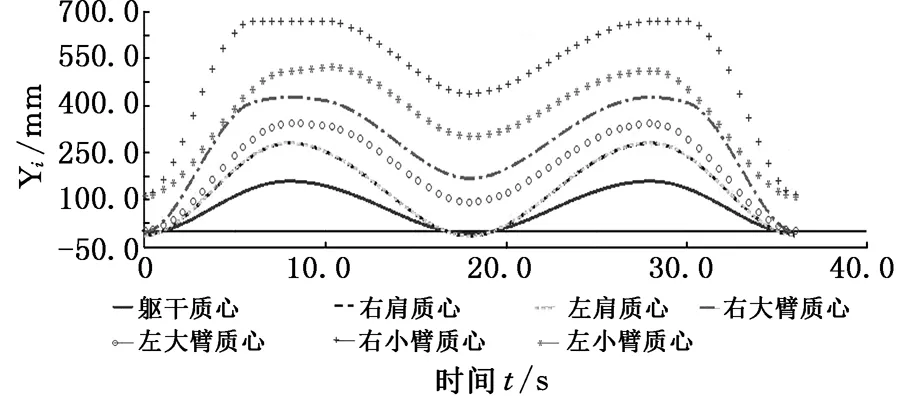
图5　各构件质心在y轴方向上的轨迹

图6　护理机器人重心在z轴方向上的轨迹

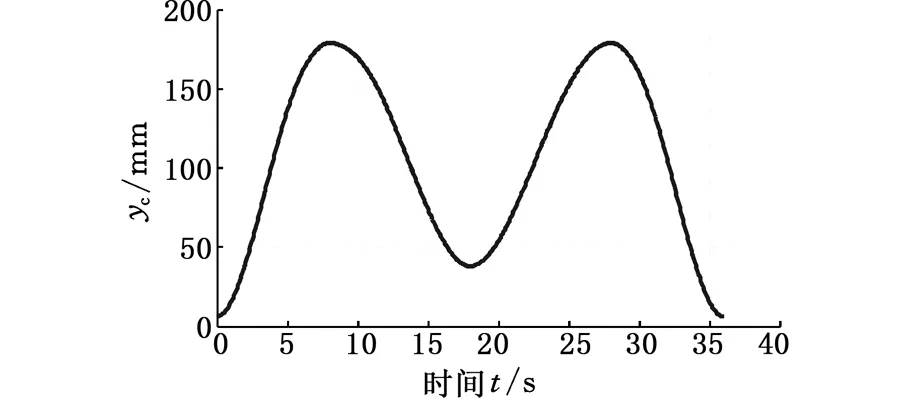
图7　护理机器人重心在y轴方向上的轨迹

2.2有负载情况下护理机器人稳定性分析

当护理机器人双臂末端施加负载时，重心投影法已不再适用此情况。为真实反映护理机器人的运动情况，本文采用ZMP理论[11]， 只要ZMP位于轮子与地面接触点形成的支撑多边形(稳定区域)内，护理机器人即处于动态稳定。由ZMP理论可以得到关于路面上任一点P的力矩平衡式如下：

(2)

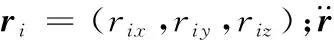
由式(2)可以看出，传统的ZMP建模中各参数是以绝对坐标系为基准的，计算量大且非常复杂，不利于实时计算调整各关节位姿状态，为此将递推牛顿-欧拉算法与传统ZMP算法相结合，采用迭代的方式计算ZMP，方便编程计算。

递推牛顿-欧拉算法如下：

(1)向外递推计算构件速度、加速度(i:0→n-1)。

(2)向内递推计算力、力矩(i:n→1)。

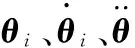
旋转矩阵

迭代初始条件

首先，根据护理机器人不同运动情况来设定迭代初始条件，利用上述递推公式求得护理机器人双臂分别施加到躯干上的力和力矩，再根据护理机器人躯干受力动态平衡求出移动平台(底座)受到的上一构件的力。此方法和静力内推方法的不同之处在于，此方法考虑了机构运动过程中产生的惯性力和力矩，更加真实反映了机构受力情况，移动平台受力如图8所示。

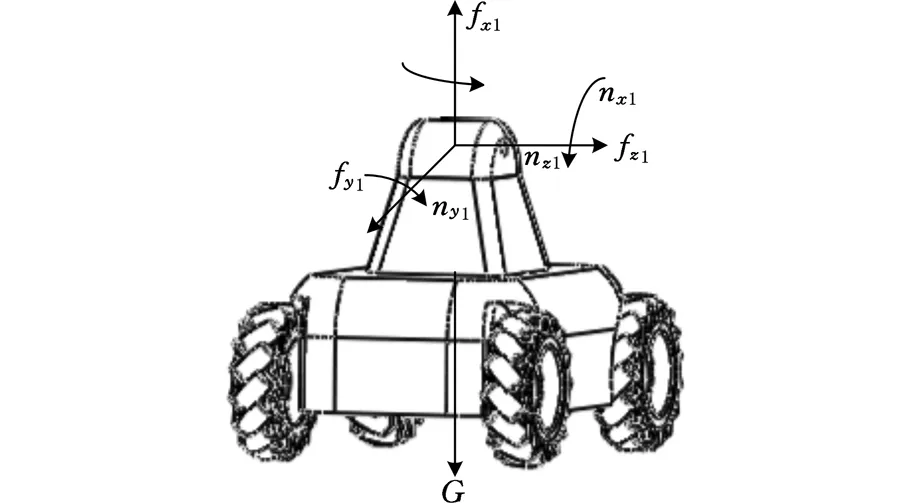
图8　移动平台受力分析

由此可得求解护理机器人ZMP(xZMP、yZMP、zZMP)的简化计算公式为

(3)

考虑到护理机器人在类似于医院的复杂非结构环境下工作，受到各种不确定因素的影响，设计中应该留出一定的安全余量，确保护理机器人在运动过程中时刻保持动态稳定性。护理机器人的4个麦克纳姆轮与地面的接触点围成一个矩形，以矩形中心为原点，以原点到矩形轮廓边界的最小距离r0为半径的圆，此区域我们定义为有效稳定安全区域。护理机器人在运动过程中，若护理机器人系统的ZMP位于有效稳定安全区域内，则护理机器人处于动态稳定，若处于有效稳定安全区域外，则无法保证其是否处于稳定状态，需要调整各构件的运动参数来使系统的ZMP处于稳定有效区域内，判定公式为

(4)

模拟护理机器人抱起体重80kg的人，为方便研究将人体假设为刚体，同样将护理机器人以及人体模型导入ADAMS虚拟仿真软件，如图9所示，定义刚体属性、添加约束、接触参数等，采用STEP驱动函数与零负载工况设定相同。

图9　ADAMS仿真初始位置

运动仿真时间36s，步长0.06，仿真过程如图10所示。

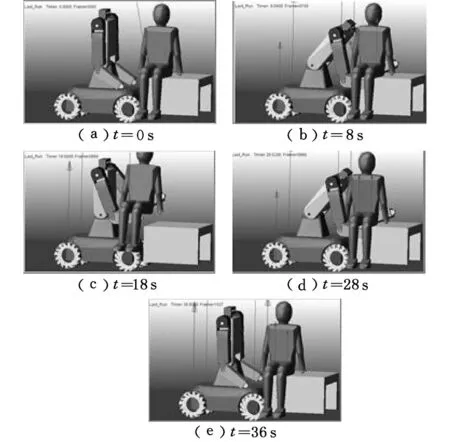
图10　护理机器人仿真流程图

图11　ZMP在y轴方向上的轨迹

图12　ZMP在z轴方向上的轨迹

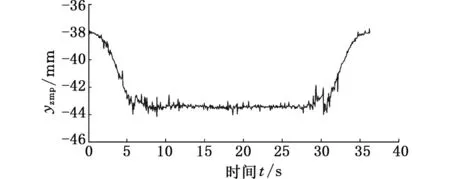
图13　ZMP在y轴方向上的轨迹

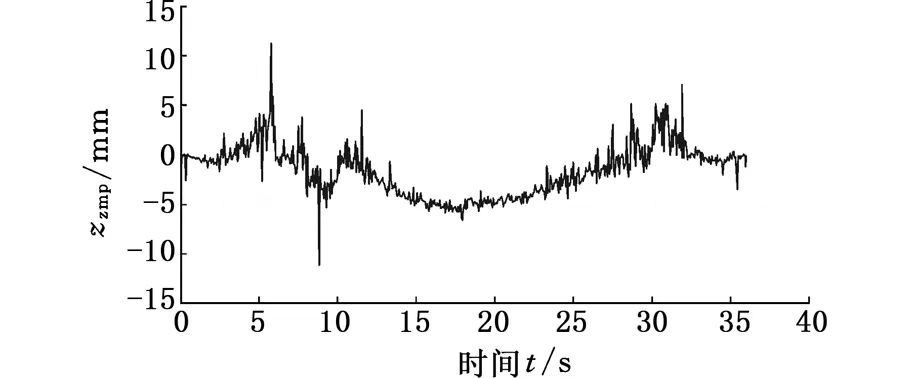
图14　ZMP在z轴方向上的轨迹

3　结语

本文针对有负载和无负载的不同工况，采用相应的稳定判定依据，从静态和动态两方面分析了护理机器人的稳定性，并利用ADAMS仿真软件模拟护理机器人的运动情况，分析护理机器人的稳定性，并提出相关稳定性判定依据，为分析护理机器人的结构合理性和验证其方案可行性提供了相关理论依据。在非结构环境下，由于受环境的不确定性和运动复杂性等因素的影响，护理机器人在某个运动瞬间极易产生突变，严重影响系统的稳定性，因此，非线性系统中的自身扰动和外部干扰对护理机器人稳定性影响将是以后研究的重点方向。

[1]郭新,安军防,黄咏梅.战场伤员转运担架的研究进展[J]. 医疗卫生装备, 2010,31(11): 40-41.

GuoXin,AnJunfang,HuangYongmei.ResearchProgressofBattlefieldTransferLitterforWounded[J].ChineseMedicalEquipment, 2010, 31(11): 40-41.

[2]嵇鹏程,沈惠平. 服务机器人的现状及其发展趋势[J]. 常州大学学报(自然科学版), 2010,22(2):73-78.

JiPengcheng,ShenHuiping.CurrentSituationandDevelopmentTrendofServiceRobot[J].JournalofChangzhouUniversity(NaturalScienceEdition), 2010,22(2):73-78.

[3]黄敦华,李勇,陈容红. 医疗服务机器人应用与发展研究报告[J]. 机电产品开发与创新,2014,27(03):6-8.

HuangDunhua,LiYong,ChenRonghong.TheApplicationsandDevelopmentReportofMedicalServiceRobot[J].Development&InnovationofMachinery&ElectricalProducts, 2014,27(3):6-8.

[4]李艳杰,钟华. 轮式仿人机器人的ZMP建模及动态稳定判据[J]. 沈阳理工大学学报, 2009,28(1):79-84.

LiYanjie,ZhongHua.TheZMPModelingandtheDynamicStabilityCriterionoftheWheelBasedHumanoidRobot[J].TransactionsofShenyangLigongUniversity, 2009,28(1):79-84.

[5]李艳杰,吴镇炜,钟华. 一种基于反作用力的仿人机器人ZMP建模与测量[J]. 仪器仪表学报,2006, (S2):1094 - 1096.

LiYanjie,WuZhenwei,ZhongHua.MedelingandMeasurementofZMPofaHumanoidRobotBasedonReaetion[J].ChineseJournalofScientificInstrument, 2006, (S2):1094-1096.

[6]WangJingguo,LYangmin.StaticForceAnalysisforaMobileHumanoidRobotMovingonaSlope[C]//IEEEInt.Conf.onRoboticsandBiomim-etics.Bangkok,Thailand, 2009:371-376.

[7]ErbaturK,OkazakiA.AStudyontheZeroMomentPointMeasurementforBipedWalkingRobots[C]//IEEE7thInternationalWorkshoponAdvancedMotionControl.Harbin, 2002: 431-436.

[8]MingD,YukiM.Lift-upMotionGenerationofNursing-careAssistantRobotBasedonHumanMuscleForceandBodySoftnessEstimation[C]// 2014IEEE/ASMEInternationalConferenceonAdvancedIntelligentMechatronics(AIM).Besançon, 2014:1302-1307.

[9]ToshiharuM,ShinyaH.Whole-BodyContactManipulationUsingTactileInformationfortheNursing-CareAssistantRobotRIBA[C]//2011IEEE/RSJInternationalConferenceonIntelligentRobotsandSystems.SanFrancisco, 2011:25-30.

[10]蔡自兴.机器人学[M].北京：清华大学出版社,2009.

[11]张涛.机器人引论[M].北京：机械工业出版社,2010.

(编辑华中平)

Analysis of Motion Stability of a Mobile Humanoid Nursing Robot

Yun Jintian1,2Deng Lihao1,2Sang Hongqiang1,2

1. Advanced Mechatronics Equipment Technology Tianjin Area Major Laboratory,Tianjin， 300387 2. Tianjin Polytechnic University, Tianjin, 300387

When a nursing robot assisted medical staff to take good care of the patients, the motion stability of the robot was the most concern, which was directly related to the success or failure of the nursing tasks. When the nursing robot lifted the patients with arm and waist, tilting and sliding would most likely to occur. Herein, an omni-directional mobile humanoid nursing robot was taken as the research object, and the motion stability was analyzed from two aspects of static and dynamic. Under the conditions of no load and low speed motion, centre of gravity projection method was used to analyze the static stability; under the load conditions, the theory of ZMP combined with the theory of recursive Newton Euler algorithm was used to analyze the dynamic stability. ADAMS was used to simulate the robot’s movement process, which provides the theoretical and simulation basis for the nursing robot stability.

nursing robot; motion stability; centre of gravity projection method; zero moment point(ZMP); recursive Newton-euler algorithm

2015-10-27

国家自然科学基金资助项目(51205287)；天津市高等学校科技发展基金计划资助项目(20110402)

TP242.6

10.3969/j.issn.1004-132X.2016.17.006

贠今天，男，1970年生。天津工业大学天津市现代机电装备技术重点实验室教授、博士。研究方向为多体动力学与控制。邓利浩，男，1989年生。天津工业大学机械工程学院硕士研究生。桑洪强，男，1978年生。 天津市现代机电装备技术重点实验室教授。