基于有限元分析的滚齿SLD构建
李国龙 赵 君 刘小旭 杨 勇
1.重庆大学机械传动国家重点实验室,重庆,4000302.重庆机床(集团)有限责任公司,重庆,400055
基于有限元分析的滚齿SLD构建
李国龙1赵君1刘小旭1杨勇2
1.重庆大学机械传动国家重点实验室,重庆,4000302.重庆机床(集团)有限责任公司,重庆,400055
针对稳定性耳垂线图(SLD)应用于滚齿颤振预测时存在动力学参数获取困难、切削深度难以确定等问题,建立了考虑滚刀刀杆柔性的三维滚齿系统动力学模型,通过滚刀极限切屑厚度与轴向进给量的关系计算滚齿系统动力学参数,并在此基础上绘制出滚齿SLD。设计了滚齿颤振实验方案,通过采集的实验数据分析平稳切削与颤振切削振动的特征量,确定颤振频率及颤振主体,证实了所建立的动力学模型及SLD的有效性。所提方法为滚齿工艺颤振预测、切削参数选取提供了一种新手段。
滚齿;颤振;稳定性耳垂线图;有限元分析
0 引言
在滚齿过程中,当系统结构参数或切削参数选用不当时,刀具与工件之间会产生强烈的自激振动,即产生滚齿“颤振”。颤振使滚齿过程不稳定、齿面质量和金属切除率下降,严重时甚至会破坏滚刀和滚齿机,是制约滚齿机加工能力的一个主要因素[1]。抑制颤振的可行途径是通过改变系统的结构参数或预测颤振发生的临界条件[2-4]。颤振临界条件的预测主要有三种方法:稳定性耳垂线图(stability lobe diagram,SLD)、Nyquist曲线和有限元分析。其中,SLD可简单而清晰地描述切削稳态与非稳态随切削深度与速度变化的过程,进而预测系统的稳定性,并有助于切削速度和深度的合理选取,因而在切削颤振分析中得到广泛应用[5]。
目前,SLD主要应用于理论切削深度恒定的车削工艺中,用于滚齿工艺时遇到两个难点:①滚齿由一系列展成运动构成,不是单纯的正交切削即进给方向始终垂直于工件表面,而滚削过程中的切削方向随着刀刃切入切出而不断变化,因而滚齿SLD中的极限切削宽度不再表现为径向吃刀量沿刃倾角的分量;②SLD所需的动力学参数一般通过实验获取,而滚齿中获取动力学参数尤其是动态切削力系数的相关实验非常困难,若采用动态实验并辅以数据处理,则结果误差较大。
本文提出基于有限元法进行滚削工艺的三维动力学仿真,将滚齿加工的顶刃最大切屑厚度与SLD中的极限切削宽度联系起来,并利用模态分析确定SLD所需的动力学参数,以构建符合滚齿实际工况的SLD。本文方法能使简单清晰的SLD应用于复杂滚齿工艺中,为滚齿工艺颤振预测、切削参数选取提供参考。
1 滚齿加工的仿真前处理及结果
1.1滚齿加工的结构参数选取
滚齿系统稳定性因素分为两类[6]:①工艺系统固有特性,包括滚齿机、滚刀、齿轮、夹具的结构形式、齿轮夹具的定位及固定方式等;②滚削工艺参数。
选取的滚齿系统结构参数如下:直齿圆柱齿轮模数m=6.5 mm,齿数Z=20,分度圆压力角α=20°;A级阿基米德滚刀外径de=110 mm,孔径d=32 mm,全长L=100 mm,容屑槽数Zg=9。滚刀主要结构参数如图1所示。

图1 滚刀结构参数及其三维模型
滚刀以螺旋升角安装在刀架轴上,滚齿仿真时将其视为刚体,则加工振动最终反映在刀架轴上。另外,因齿轮轴刚度远大于刀架轴刚度,齿轮安装部分也可视为刚体。故本文主要讨论刀架轴结构参数对振动的影响。
由于颤振频率总是接近于系统薄弱环节的某阶模态固有频率[7],滚刀部件为滚齿系统的薄弱环节,故滚齿颤振将出现在刀架轴的某阶固有频率上,对刀架轴结构参数进行优化,可有效提高滚齿系统的抗颤振能力[8-9]。
1.2滚齿加工仿真模型的建立
选用ABAQUS/Explicit有限元软件,在不考虑热变形的前提下,将滚刀简化为刚体、刀架轴简化为简支梁,得到滚齿简化模型,如图2所示。

图2 滚齿模型
首先,确立材料模型。采用Jonhson-Cook强度模型,其应力与应变、应变率及温度的关系为
(1)
式(1)等号右边第一个圆括号代表材料弹塑性行为,第一个中括号代表材料黏性,第二个中括号代表材料的热软化效应。A、B、n为材料应变强化项系数,C为材料应变速率强化项系数,m为材料热软化系数。A、B、C、m、n通过实验测得。
针对切屑断裂失效,采用ABAQUS/Explicit的剪切失效准则与Jonhson-Cook断裂准则设置参数。Jonhson-Cook断裂准则本构方程为
(2)

材料AISI4340的性能参数见表1,材料失效参数见表2。

表1 AISI4340材料性能参数

表2 AISI4340材料失效参数
1.3滚齿加工参数的确定
滚齿切削运动较为复杂,既有滚刀转动与齿坯转动构成展成运动,又有滚刀沿齿坯轴线的进给运动以及由此产生的齿坯附加转动。滚齿切削宽度主要表现为展成过程中滚刀顶刃能够切削的最大切屑厚度h1max,如图3所示。

图3 顶刃最大切削厚度h1max
采用Hoffmeister建立的滚齿顶刃切屑厚度与工件轴向进给量的关系式[10-14]:
fa=Fh1FmFZ2FdFN/Z0Fa
(3)
其中,Fh1、Fm、Fz2、Fd、FN/z0、Fa为6个影响因子,其计算式见表3。表3中,h1max为滚刀顶刃的最大切屑厚度,mm;fa为滚刀轴向进给量,mm/r ;β为齿轮分圆螺旋角,rad。
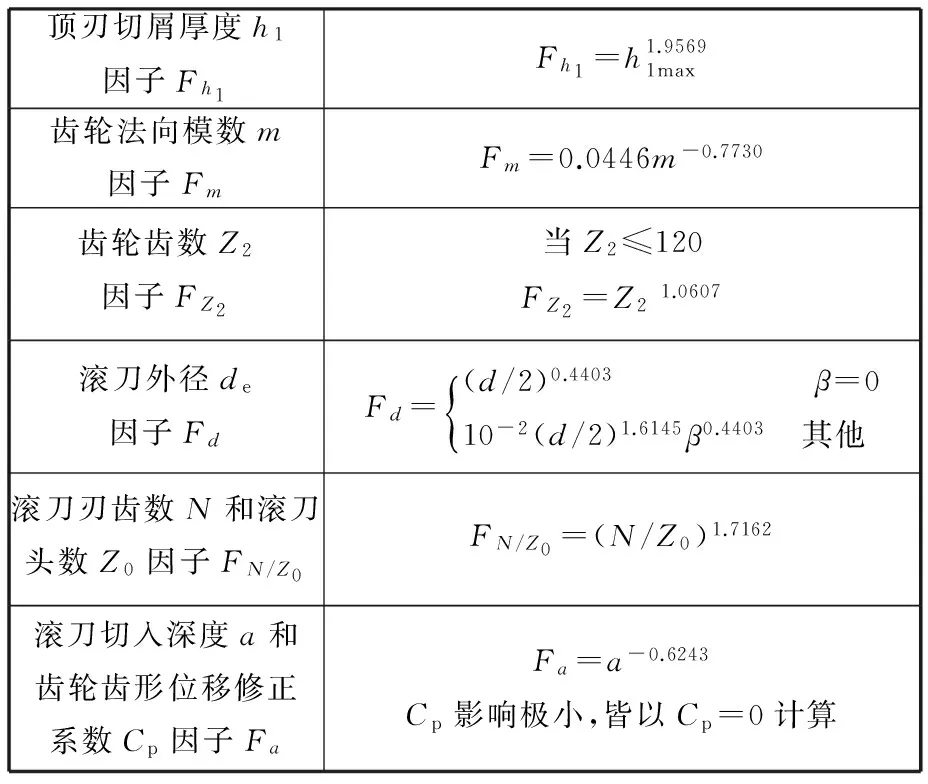
表3 fa各影响因子计算公式
滚削加工一般作为剃前或磨前工艺,滚刀切入深度即吃刀量取a=2.25mn。根据式(3),在已知滚刀结构参数与齿轮参数的前提下,通过选取不同的轴向进给量,计算出对应的顶刃最大切屑厚度h1max,可为仿真与实验参数选取提供依据。
1.4滚齿加工的动力学仿真
滚齿加工的起始位置,即切入开始时滚刀中心线距齿坯端面的距离t0的计算式如下:
(4)
h1=h-de(1-cosθ)/2
(5)
(6)
式中,h为齿轮全齿高;CZ为滚刀与齿轮的中心距;φ为滚刀分度圆螺旋升角。
从被加工齿轮的强度和齿轮滚刀材料的性能出发,滚刀切削时顶刃存在一个最大许可负荷,而负荷与切削量有着直接的关系,滚刀顶刃应规定一个最大许可切屑厚度。本文规定滚刀材料为高速钢,故综合考虑滚刀的硬质合金材料及齿坯材料,h1max选用国际标准推荐值0.49 mm,由式(3)得到相应轴向进给量fa为3 mm/r,对应的滚刀转速为214 r/min,时间长度选取1 s,采用上述参数进行动力学仿真,滚削位移分布如图4所示。

图4 滚削仿真位移分布图
由于滚刀旋转位移远大于刀架轴的振动位移,故需单独显示刀架轴以分析其振动位移,图5为刀架轴的振动位移图。

图5 刀架轴振动位移图
当轴向进给量变化时,仿真所得到的刀架轴振动位移也会发生变化,图6、图7分别为轴向进给量为4 mm/r、3 mm/r时的振动位移图。
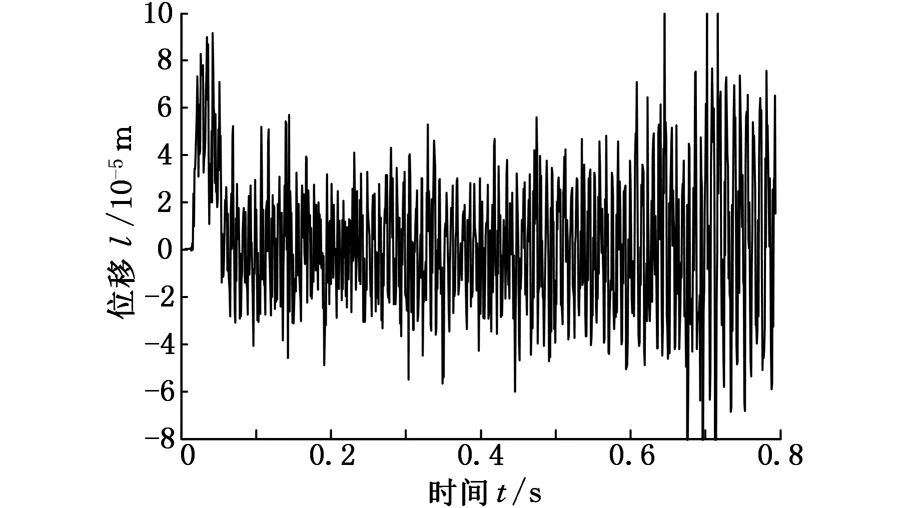
图6 fa=4 mm/r时的振动位移

图7 fa=3 mm/r时的振动位移
对比图6、图7,发现加大轴向进给量将导致颤振发生,轴向进给量变化引起滚刀顶刃切削厚度变化。通过快速傅里叶变换获得滚齿系统共振频率为760 Hz、颤振频率为836 Hz,如图8、图9所示,印证了颤振频率接近系统固有频率这一说法。另外,在共振曲线的共振频率f0峰值下3 dB处找到相应的f1和f2,用于求取阻尼比ξ,即
(7)

图8 稳定切削频域图

图9 颤振发生时的频域图
2 SLD的构建
2.1SLD建模
滚齿加工的SLD是从二维平面角度构建,其动力学模型如图10所示。

图10 滚齿的二维动力学模型
滚齿颤振系统动力学模型的振动系统运动微分方程为
(8)
其中,fd(t)为动态切削力,me为振动系统等效质量,c为振动系统等效阻尼系数,k为振动系统等效刚度,β(齿轮分度圆螺旋角)为动态切削力与X坐标轴的夹角。X向的动态切削力为
Ff=kfb[x(t-TL)-x(t)]
(9)

(10)
为简化公式,设定参数之间的关系如下:
(11)
式中,ωn为系统固有频率。
对式(10)进行拉普拉斯变换,得
(12)
由式(12)得到系统传递函数:
(13)
s=σ+jω
当σ=0时,系统处于临界状态,即系统极限切削宽度位置。其中,ω为系统的颤振频率,其值略高于ωn。
将s=jω代入式(12),得到传递函数的实部G(ω)与虚部H(ω):
由于复振动信号中只有其实部才能真实描述振动信号的物理特征,故可得复振动信号临界状态下限切削宽度blim(与极限切削宽度等价):
令ω/ωn=λ,则有
(14)

式中,n1为自然数,n1=0,1,2,…。
主轴转速为
(15)
由式(13)、式(14)可知,在已知系统的动力学参数me、c、k、kf、ξ、ωn的条件下,blim与N是λ的函数。
2.2SLD参数的确定
首先,通过有限元静力分析得到刀架轴连接点刚度(振动系统方程的等效刚度)kh=209.8MN/m。滚齿强迫再生颤振发生时,因颤振为滚齿误差的主要来源,故可将滚刀部件的固有频率作为滚齿系统的固有频率。
基于ABAQUS进行模态分析[15],提取滚刀系统的前6阶特征值以及相关参数,见表4。其中TOTALMASSOFMODEL(模型可运动质量)值为9.857 152。

表4 滚刀系统振动参数
根据分析得到的各阶模态参与系数,第4阶振型主要在X方向上作用,且X向的总有效质量超过模型可运动质量的90%,模态提取合理。由表4可得ωn=4812.5,系统等效质量为数据中的广义质量,me=9.0635。
在确定等效阻尼c时,采用Rayleigh阻尼进行瞬态动力学分析,公式如下:
C=α1M+β1K
(16)
其中,阻尼矩阵参数C是质量矩阵M和刚度矩阵K的线性组合,参数α1主要对低阶频响发挥作用,参数β1主要对高阶频响发挥作用,而颤振主要发生在低阶频响段,故只考虑参数α1。
取阻尼比ξ=0.038,通过式(10)求得系统等效阻尼c=3314.98,系统等效刚度k=209.8 MN/m。动态切削力系数kf表现为机床结构的动柔度和切削过程的动态特性。滚削力的变化由参与滚削的滚刀齿的切削量共同决定,通过滚齿动力学仿真得到0.2 s时的滚削力变化曲线,如图11所示。
在三维CAD软件SolidWorks中,通过布尔运算求得0.2s时总切屑量为2.362mm3,计算每个波峰波谷对应的动态切削力变化量,加权平均并除以总切屑量,得到kf=2.624×1010。使用MATLAB软件绘制出SLD,如图12所示。

图11 滚削力变化曲线
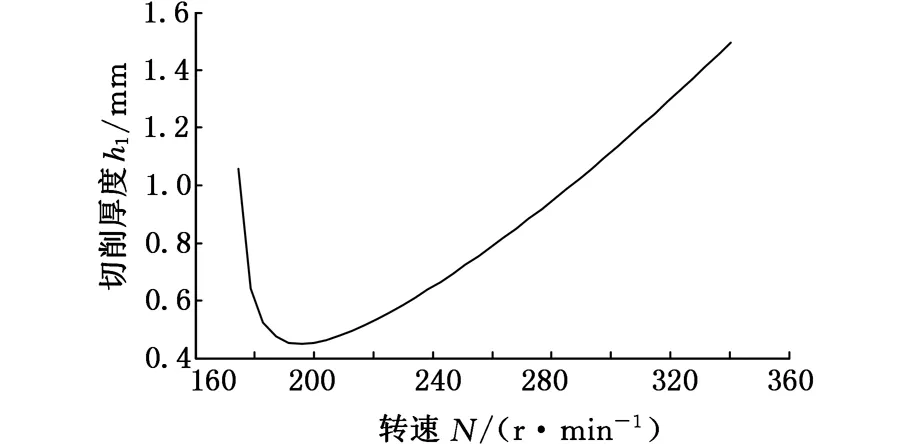
图12 滚刀转速214 r/min附近的SLD
在图12中选取转速214r/min附近的6个点进行仿真分析,得到表5所示的极限切厚。当滚刀转速为214r/min时,其极限切厚为0.5mm,略大于推荐值h1max=0.49mm。因此,基于有限元仿真求取滚齿动力学参数进而构建SLD具有可行性。

表5 SLD上6点对应的极限切屑厚度
3 SLD的实验验证
3.1实验方案
在齿坯及滚刀结构参数给定且转速保持不变的情况下逐步加大轴向进给量fa,若工件表面有清晰振痕且产生强烈噪声时,认为系统发生了颤振。由时域信号分析及傅里叶变换可以看到,颤振时的振动信号幅值明显大于正常切削状态时振动信号的幅值,颤振频率出现在切削系统某阶固有频率附近,并且颤振能量集中在很窄的范围内。
如图13所示,通过传感器信号采集,并进行数据处理,将发生颤振的轴向进给量转换为最大切屑厚度h1max记录下来。
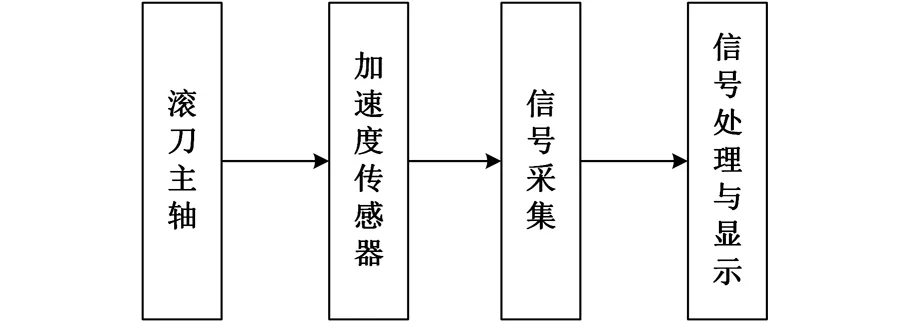
图13 实验方案
如表6所示,改变轴向进给量,重复以上步骤。

表6 主轴转速对应的不同轴向进给量
3.2实验器材及布置
利用加速度传感器测量滚刀与齿轮轴X向上的振动加速度,并通过二次积分来反映滚齿系统的振动位移变化情况,实验器材见表7。

表7 滚齿颤振实验器材
因滚刀及齿轮均要旋转,故将带磁座加速度传感器分别布置在刀架轴的防护罩壳和齿轮轴的顶尖导轨上,如图14所示。信号在线测量界面如图15所示。

图14 加速度传感器现场安装位置
图15 信号在线测量界面
3.3实验结果
3.3.1 空转
将滚刀调整到切削位置,主轴转速调整到200 r/min,滚齿机空转加工,提取滚齿机稳定运行时滚刀轴与齿轮轴在X方向上的自功率谱曲线,如图16、图17所示。空转时,滚刀轴X方向在338 Hz处振幅取得最大值0.142 m/s2,齿轮轴X方向在500 Hz处振幅取得最大值0.128 m/s2。

图16 空转时滚刀轴X方向自谱曲线

图17 空转时齿轮轴X方向自谱曲线
3.3.2平稳切削(轴向进给量为2.7 mm/r)
由图18、图19可知,滚刀轴在830 Hz附近振幅略有增加,其他处变化不大,X方向在898 Hz处最大振幅为0.28 m/s2;齿轮轴X向的峰值主要发生在492 Hz和1200 Hz附近,其大小为0.14 m/s2。另外,平稳切削与空转振动幅值接近。

图18 平稳切削时滚刀轴X方向自谱曲线
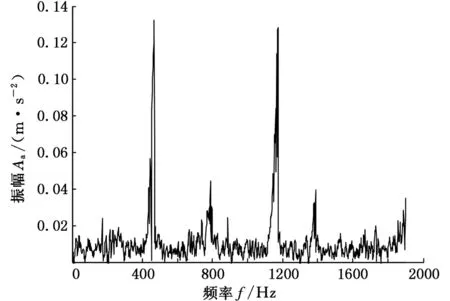
图19 平稳切削时齿轮轴X方向自谱曲线
3.3.3颤振切削
逐渐加大轴向进给量,当轴向进给量达到2.9 mm/r时,系统发生颤振,如图20所示。

图20 颤振发生时滚刀轴X方向自谱曲线

图21 颤振发生时齿轮轴X方向自谱曲线
由图20可知,当轴向进给量至2.9 mm/r时,刀架轴在850 Hz附近发生颤振,其X方向的最大振幅为7 m/s2,其他处变化不大。由图21可知,齿轮轴仍在492 Hz和1200 Hz附近振幅达到X向最大值,其值0.19 m/s2也与平稳切削时的振幅接近。
平稳切削(轴向进给量为2.7 mm/r)时,切削过程平稳、无刺耳噪声、工件表面光滑、无振纹,如图22所示。继续加大轴向进给量,当进给量达到2.9 mm/r时,振幅在颤振频率范围内明显增大,且噪声刺耳、齿面出现鱼鳞状振纹,此时系统发生颤振,如图23所示。

图22 平稳切削齿面 图23 颤振切削齿面
通过实验发现:颤振发生时,滚刀转速为200 r/min,轴向进给量所对应的顶刃切屑厚度按式(2)计算为0.488 mm,处于所构建的SLD曲线附近;滚齿系统的颤振频率在830~850 Hz之间,与滚刀部件的固有频率接近,颤振优先发生于滚刀部件。实验得到的稳定切削深度点与基于仿真方法绘制的SLD得到的相关数据点基本一致,验证了通过仿真方法获得SLD的正确性。
4 结论
(1)本文通过选择合适的材料、本构模型与切屑断裂准则与失效准则,建立了圆柱直齿轮滚削的有限元模型,在此基础上,构建了能够反映不同轴向进给量与滚削速度下预测滚齿加工稳定性的动力学模型。
(2)通过滚齿有限元仿真得到相关动力学参数,并将滚齿极限切屑厚度与轴向进给量联系起来,实现了SLD在滚削工艺中的应用。
(3)构建了颤振实验方案,通过实验验证了动力学仿真结果与构建的SLD的正确性,得到该滚齿系统的颤振频率范围及颤振主体。
(4)本文方法对于预测滚削颤振、选取合适的切削参数,具有一定的参考价值。
[1]Huang Qiang,Zhang Genbao,Chen Kun. Continuity and Break of Chatter Vibration Status[J].Chinese Journal of Mechanical Engineering,2008,21(4):92-96.
[2]王跃辉,王民.金属切削过程颤振控制技术的研究进展[J].机械工程学报,2010,46(7):166-174.
Wang Yuehui,Wang Min.Advances on Machining Chatter Suppression Research[J].Journal of Mechanical Engineering,2010,46(7):166-174.
[3]王民,费仁元.基于电流变材料的切削颤振在线监控技术研究[J].机械工程学报,2002,38(12):93-97.
Wang Min,Fei Renyuan.Research on Monitored Control of Machining Chatter Based on Electrorheological Fluids[J]. Journal of Mechanical Engin-eering,2002,38(12):93-97.
[4]Behnam M I, Yussefian N Z. Dynamic Simulation of Boring Process[J]. International Journal of Machine Tools and Manufacture,2009,49(14):1096-1103.
[5]Meritt H E.Theory of Self-excited Machine-tool Chatter[J].Transactions of the ASME Journal of Engineering for Industry,1965,87: 447-454.
[6]杨勇,王时龙,田志峰,等.大型数控滚齿机立柱动力学仿真分析[J].中国机械工程,2013,24(11):1473-1479.
Yang Yong,Wang Shilong,Tian Zhifeng,et al.Dynamics Simulation Analysis of Column for Large-scale NC Gear Hobbing Machines[J].China Mechanical Engineering, 2013,24(11):1473-1479.
[7]阎兵,张大卫,徐安平,等.球头刀铣削过程动力学模型[J].机械工程学报,2002,38(5):22-26.
Yan Bing,Zhang Dawei,Xu Anping,et al.Dynamic Modeling of Ball End Milling[J].Journal of Mechanical Engineering,2002,38(5):22-26.
[8]刘润爱,张根保,黄强,等.提高零传动滚齿机系统刚度的研究[J].系统仿真学报,2006,18(3):710-712.
Liu Run’ai,Zhang Genbao,Huang Qiang,et al.Study on System Stiffness Enhancement of Zero-drive Gear Hobbing Machine[J].Journal of System Simulation,2006,18(3):710-712.
[9]吴化勇.高速切削系统动态特性研究[D].济南:山东大学,2005.
[10]Sima M, Ozel T.Modified Material Constitutive Models for Serrated Chip Formation Simulations and Experimental Validation in Machining of Titanium Alloy Ti-6A-4V[J].International Journal of Machine Tools & Manufacture,2010,50(11):943-960.
[11]Oze T, Zeren E. Finite Element Method Simula-tion of Machining of AISI 1045 Steel with a Round Edge Cutting Tool[C]//Proceedings of 8th CIRP International Workshop on Modelling of Machining Operations. Chemnitz,2005:533-541.
[12]Altintas Y.Manufacturing Automation[M].Cambridge: Cambridge University Press,2000.
[13]Mahnama M, Movahhedy M. Application of FEM Simulation of Chip Formation to Stability Analysis in Orthogonal Cutting Process[J].Journal of Manufacturing Processes,2012,14(3):188-194.
[14]朱育权,千学明,林晓萍.1CL50型机床立柱振动模态分析[J].西安工业大学学报,2007,27(3):215-218.
Zhu Yuquan,Qian Xueming,Lin Xiaoping.Modal Analysis of a Column of 1CL50 Machine Tools[J].Journal of Xi’an Technological University,2007,27 (3):215-218.
[15]成群林,柯映林,董辉跃,等.高速硬加工中切屑成形的有限元模拟[J]浙江大学学报(工学版),2007,41(3):509-513.
Chen Qunlin,Ke Yinglin,Dong Huiyue, et al. Simulation of Chip Formation in High-speed Hard Machining[J].Journal of ZhejiangUniversity(Engineering Science), 2007,41(3):509-513.
(编辑陈勇)
作者简介:李国龙,男,1969年生。重庆大学机械传动国家重点实验室教授、博士研究生导师。主要研究方向为精密制齿技术与装备、智能数控技术等。获省部级一等奖1项,发表论文40余篇。赵君,男,1991年生。重庆大学机械传动国家重点实验室硕士研究生。刘小旭,男,1988年生。重庆大学机械传动国家重点实验室硕士研究生。杨勇,男,1980年生。重庆机床(集团)有限责任公司检测技术研究所所长、高级工程师、博士。
Construction of SLD in Gear Hobbing Process Based on FEA
Li Guolong1Zhao Jun1Liu Xiaoxu1Yang Yong2
1. The State Key Laboratory of Mechanical Transmissions, Chongqing University,Chongqing,400030 2. Chongqing Machine Tool(Group) Co., Ltd., Chongqing,400055
Aiming at the problems of predicting gear hobbing chatters by SLD where the dynamics parameters were hard to get and the cutting depth was hard to determine, a 3D gear hobbing system dynamics model was established considering cutters arbor flexibility of hob. Hobbing system dynamics parameters was calculated with the relationship between limit chip thickness of hob and axial feed. And the SLD of gear hobbing was drawn based on the model. A hobbing chatter experiment plan was designed, features of steady state cutting and chatter cutting was analyzed via experimental data collected, and chatter frequency and chatter subject was determined, the validity of dynamics model established and SLD was verified. It provides a new method to predict hobbing chatter and to choose cutting parameters.
hobbing; chatter; stability lobe diagram (SLD); finite element analysis(FEA)
2015-06-17
国家科技支撑计划资助项目(2014BAF08B02);重庆市科技人才培养计划资助项目(cstc2013kjrc-qnrc70001)
TG156
10.3969/j.issn.1004-132X.2016.17.003
文泽军,男,1966 年生。湖南科技大学机械设备健康维护湖南省重点实验室教授、博士。主要研究方向为机电系统动力学与控制、制造系统质量控制、制造过程监测与控制和面向产品制造/装配过程的稳健设计。刘湛,男,1990年生。湖南科技大学机电工程学院硕士研究生。金永平,男,1984 年生。中南大学机电工程学院博士研究生。田续玲,女,1975年生。湖南科技大学海洋矿产资源探采装备技术湖南省工程实验室助理研究员。黄良沛,男,1971年生。湖南科技大学机械设备健康维护湖南省重点实验室教授。

