五自由度3D打印并联机器人设计及分析
潘 英 方跃法 汪丛哲
北京交通大学,北京,100044
五自由度3D打印并联机器人设计及分析
潘英方跃法汪丛哲
北京交通大学,北京,100044
为实现多向3D打印,设计了一种新型五自由度3D打印并联机器人,该机器人具有两个转动自由度和三个平动自由度,其特点是采用铰接的动平台以获得大的工作空间。根据建立的运动学模型,计算了该机器人机构的运动学反解,分析了定姿态位置工作空间和定位置姿态工作空间,用螺旋理论方法建立了速度雅可比矩阵,在此基础上分析了五自由度3D打印并联机器人的奇异性、灵巧性,并进行了运动仿真分析。研究结果表明,所设计的五自由度3D打印并联机器人具有大的位置工作空间和姿态工作空间,该机器人在工作空间内存在奇异位置,通过添加冗余驱动后可以消除奇异位置,并且具有良好的灵巧性,适合多向3D打印。
多向3D打印;并联机构;大工作空间;奇异性;冗余驱动
0 引言
3D打印技术也称增材制造技术,与传统的去除材料加工技术完全不同,是通过逐层增加材料来生成3D实体。有人指出,3D打印技术与当今发达的数字技术相结合,再加上互联网的普及以及微小而成本低廉的电子电路的广泛使用,将会打开第三次工业革命的大门[1]。
国内外很多学者对3D打印进行了研究[2-5],并提出了一种多向打印的概念,这种多向3D打印可以把材料沿着不同方向累积到成形的表面,提高了分层制造的质量,但要求机器人至少具有4个自由度。Lee等[6]设计了一种五自由度的3D打印机器人以实现多向打印。Keating等[7]把3D打印技术和多轴铣等加工技术结合到一起,用六自由度的KUKA KR5 sixx R850机器人实现了多功能和多材料的加工。但上述机器人主要采用的是串联机构,串联机构惯性大、误差较大,目前市场上的大部分3D打印机器人都采用的是串联结构,打印出的产品的精度和相对复杂程度都比较低[8]。并联机构因其具有精度高、刚度大、速度快、承载能力强等优点,被广泛地应用,但并联机器人工作空间小,其应用受到了很多限制。目前基于并联机构的多向3D打印的研究相对较少,Song等[9]把Stewart并联机构应用在3D打印上,但是六自由度Stewart机构可以实现的工作空间比较小,不能满足尺寸较大的零部件的加工,且利用率较低。
本文设计了一种新型多向3D打印机器人。为保证多向3D打印机器人末端执行器刚度与运动的精度,采用并联机构,通过4个平行四边形结构与动平台、定平台组成闭环结构;为获得大的工作空间,采用具有可变机构的动平台(铰接动平台)。
1 机构简述
如图1a所示,本文分析的3D打印并联机器人模型由动平台、定平台、支撑杆、驱动滑块、平行四边形连杆、连杆PL和连杆PR组成,连杆PL和PR与支撑杆由复合支链PRPaR连接,其中P表示移动副、R表示转动副、Pa表示由4个R副组成的具有平行四边形机构的复合运动副。动平台与连杆PL和PR通过R副连接,如图1b所示,PL和动平台中间连杆PM之间由转动副R3连接,PR杆和动平台由转动副R1连接。

(a)2R3T_PM机器人三维模型
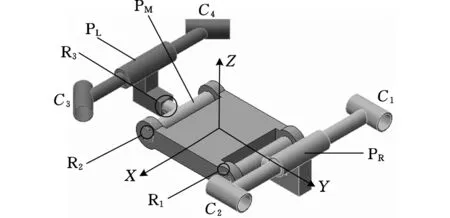
(b) 2R3T_PM铰接动平台图1 2R3T_PM三维模型
传统的刚体动平台自身没有自由度,连杆与连杆之间或连杆与动平台之间具有较大的干涉作用,并联机器人的工作空间受到很大的限制。本文分析的并联机器人的动平台区别于传统的刚体动平台,具有一个被动转动关节R2,图1b所示是一种铰接动平台,可以实现绕X轴的转动。由于4个复合支链PRPaR和刚性动平台构成的并联机构(H4)具有三个移动的自由度和一个绕Z轴转动的自由度[10],故本文设计的3D打印并联机器人把铰接动平台与4个复合支链PRPaR连接,可以实现三个自由度的移动和两个自由度的旋转,并把该五自由度3D打印并联机器人命名为2R3T_PM。
2 运动学反解分析
2.1几何模型
2R3T_PM3D打印并联机器人的几何模型见图2,定坐标系为ObXbYbZb,动坐标系为OXYZ,O位于动平台的中心,O1、O2和O4分别为运动副R1、R2和R3的中心,O3为连杆PR的中心,且在Y轴上,Ci(i=1,2,3,4)分别表示PL杆和PR杆与Pa的连接运动副的中心,Aj(j=1,2,3,4,5)表示驱动部件运动副中心,Bi(i=1,2,3,4)表示驱动部件与Pa的连接运动副中心。参数l1、l2、l3、r1、r2、r3分别表示BiCi、C1C2、C3C4、O1O2、O1O3、O2O4的长度,r4表示O4到C3C4或O3到C1C2的Z方向上的距离,pj表示驱动滑块在Z方向的位置。
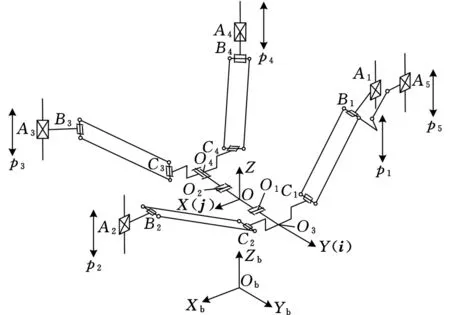
(a)2R3T_PM并联结构简图
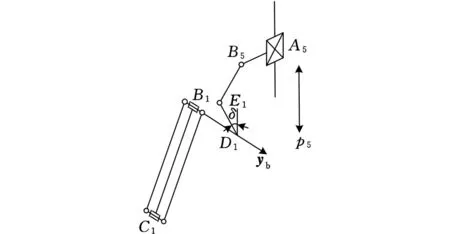
(b)支链1结构简图图2 2R3T_PM的几何模型
2.2位置反解
O在定坐标系中的位置为bo=(x,y,z)T,j和i分别表示X、Y瞬时轴,绕X、Y轴的转动可表示为先绕i轴转动角度α,再绕j轴旋转角度β,旋转矩阵分别表示为RY(α)和RX(β),则总的变换矩阵为
bRp=RY(α)RX(β)
(1)
O1和O2在动坐标系中的位置分别为
po1=(0,r1/2,0)T
po2=(0,-r1/2,0)T
可得O1和O2在定坐标系中的位置分别为
bo1=bo+bRppo1
(2)
bo2=bo+bRppo2
(3)
得Ci(i=1,2,3,4)在定坐标系中的位置为
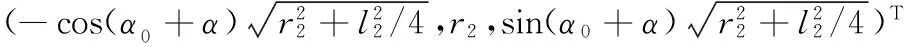
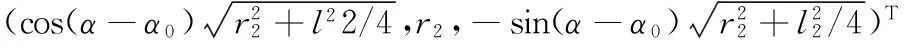
bc3=bo2+(l3/2,-r3,r4)T
bc4=bo2+(-l3/2,-r3,r4)T
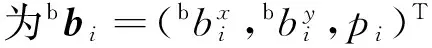
(4)
由式(4)可得驱动滑块在Z方向上的位置pi为
(5)
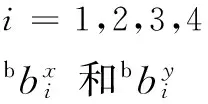
引入变量角度δ表示连杆D1E1和Zb方向上的单位向量zb的角度。如图2b所示,转动关节B1的轴线始终与Yb轴平行。D1E1垂直于转动关节B1的轴线和B1C1所在的平面,D1E1的单位向量可以表示为
其中,yb为Yb方向上的单位向量。因此
δ=arccos(nD1E1·zb)
则p5可由p1表示为
(6)
式中,l4为D1E1的长度;l5为D1B5的长度。
给定结构设计参数如表1 所示。

表1 结构设计参数 mm
3 速度雅可比矩阵
(7)
其中,Jx和Jp分别被称为并联机构的间接和直接雅可比矩阵。根据螺旋理论,动平台相对于基座的瞬时速度旋量V可以写成每条支链中的各个关节的速度以及运动副旋量的线性组合[11]。对于支链k(k=1,2)有如下关系式:
VR=1wk1$k+2wk2$k+3wk3$k+4wk4$k
(8)
j=1,2,4
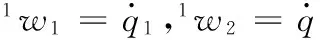
3$i是复合关节Pa的单位螺旋,可表示为
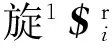
(9)
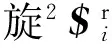
(10)
式中,nGi为GiCi的单位矢量。
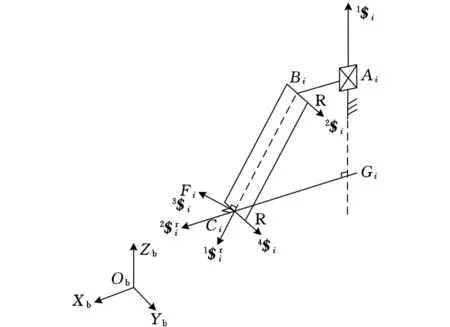
图3 螺旋量的表示
nGi可以根据下式求出:
(11)
用式(9)和式(10)与式(8)进行互易积可得
(12)
对于2R3T_PM的支链3和支链4,有与式(8)类似表达式:
VL=1wi1$i+2wi2$i+3wi3$i+4wi4$i
(13)
i=3,4
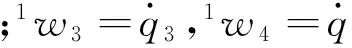
(14)
从式(8)和式(13)中可以看出螺旋VR和VL都表示与Ob瞬时重合点的速度,但分别属于连杆PR和PL。PR和PL的速度可以表示
(15)
其中,wR和vR分别表示PR杆的角速度和线速度,wL和vL分别表示PL杆的角速度与线速度。PR杆可以实现三维移动和绕Yb轴转动,所以wR=(0,wy,0)T,wy表示绕Yb轴转动的角速度。PL杆可以实现三维移动,不能转动,因此wL=0,PL杆上各点的速度都相等,所以点O4的速度vO4等于vL。因为O2和O4在同一轴线上,所以O2点的速度vO2等于vO4。化简式(15)可得
(16)
因为O1是固定在PR杆上的点,它的速度vO1可以表示为
vO1=vR+wyy×ObO1
(17)
其中,y为平行于轴Yb的单位向量。相对于PL杆,PR杆可以绕i轴和j轴旋转,即有
(18)
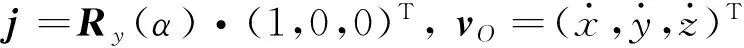
(19)
Jp=diag(A1C1×n1·1s1,A2C2×n2·1s2,
A3C3×n3·1s3,A4C4×n4·1s4,B1C1×nGi·2s1)
(20)
式(6)对时间求导可得
(21)
4 运动性能分析
4.1工作空间
机器人工作空间是机器人末端操作器的工作区域,它是衡量机器人性能的重要指标之一。并联机器人工作空间可分为定姿态的位置工作空间和定位置的姿态工作空间。
4.1.1定姿态的位置工作空间
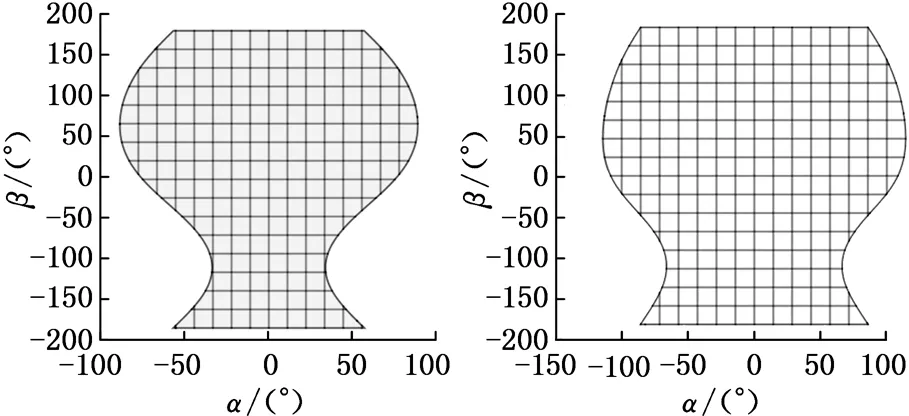
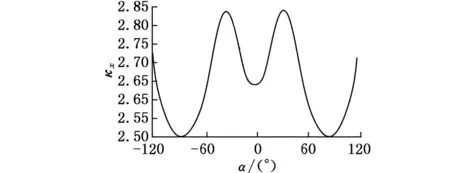
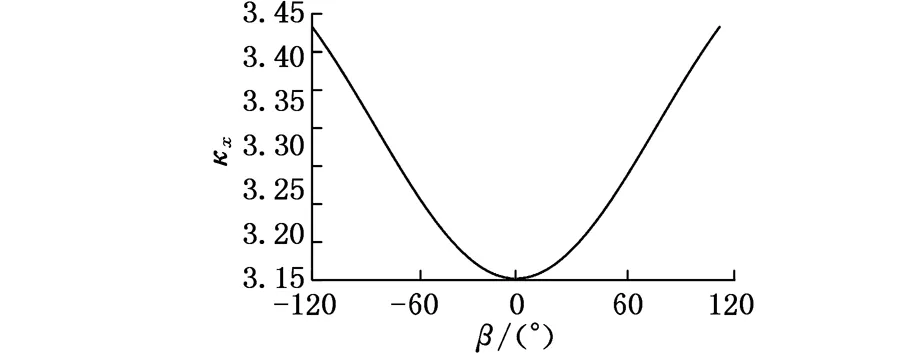
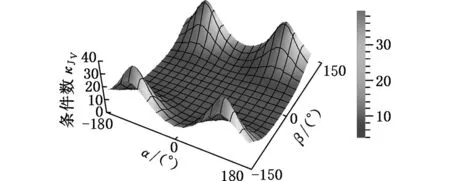
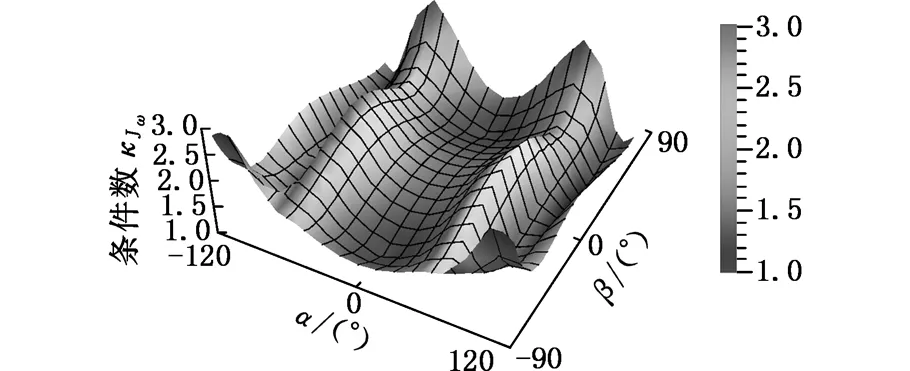
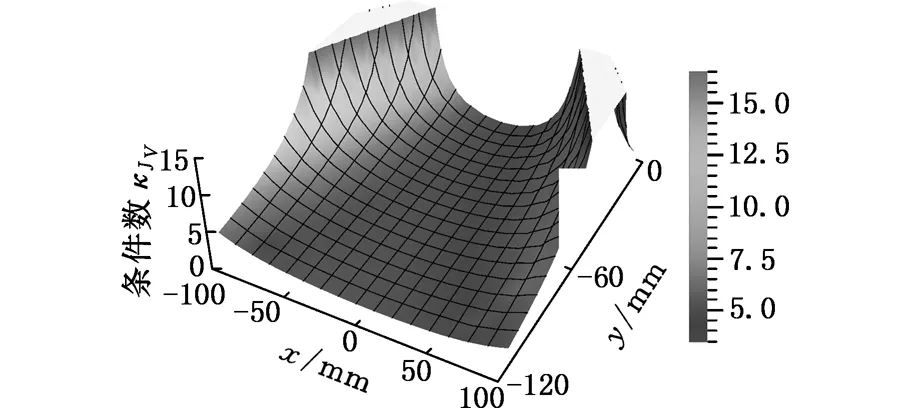
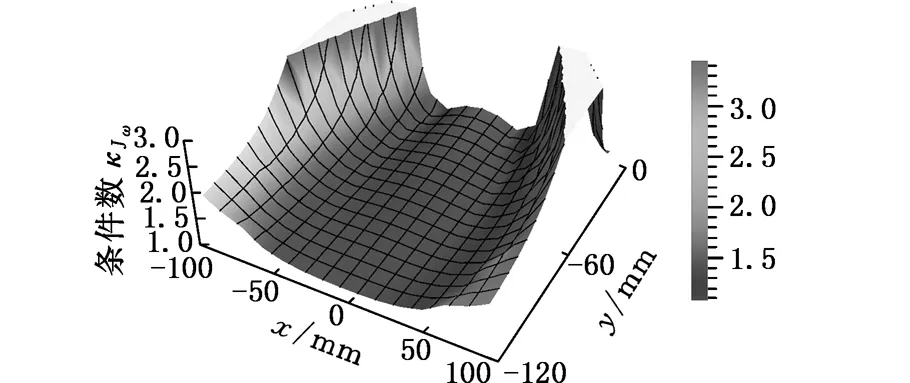
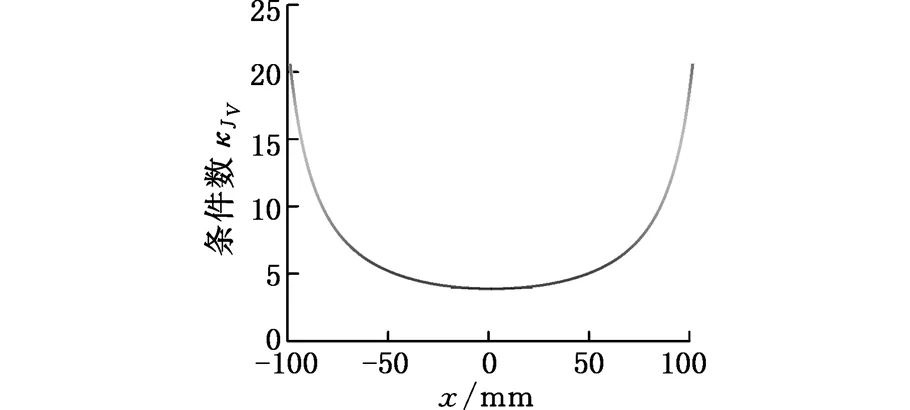
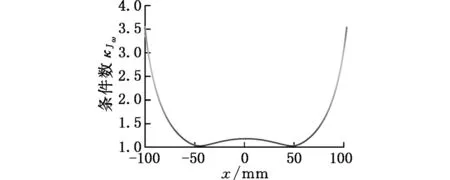
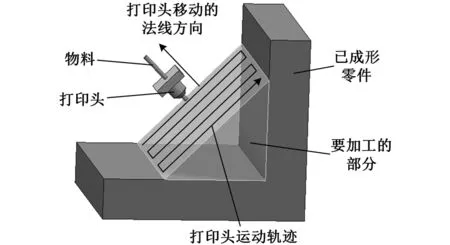
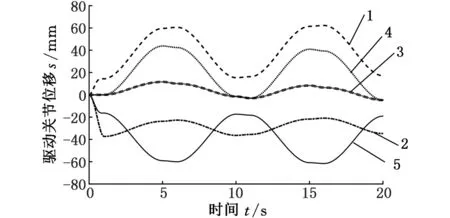
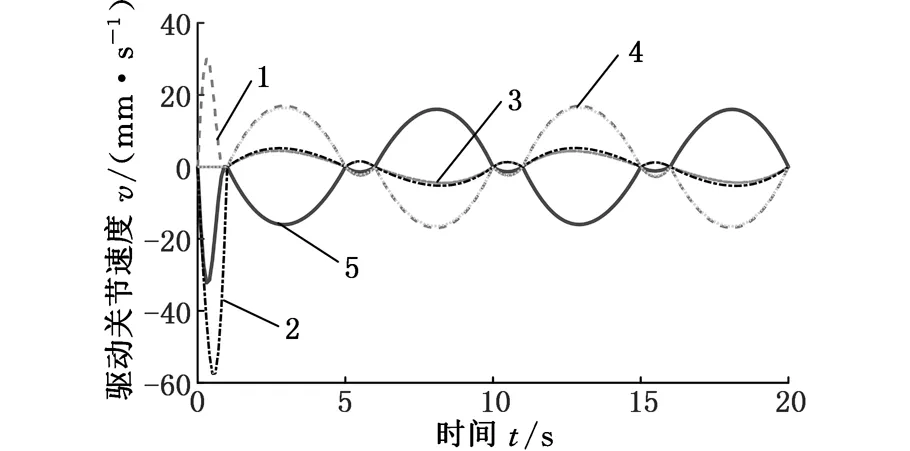
本文基于Gosselin几何法[12],利用运动学反解来分析2R3T_PM定姿态工作空间,根据杆长约束条件,取Zmin 图4 定姿态工作空间 从图4中可以得出,2R3T_PM可以像Delta和H4并联机器人一样有很大的位置工作空间,且该工作空间关于平面YbZb对称,但不关于平面XbZb对称。 4.1.2定位置的姿态工作空间 同定姿态的位置工作空间分析方法,求出2R3T_PM在定位置bo=(x,y,z)T时的姿态工作空间,图5a~图5d分别显示了bo=(0,0,175 mm)T,bo=(0,0,200 mm)T,bo=(0,0,220 mm)T,bo=(0,0,240 mm)T时的姿态工作空间。 由图5可以看出,当给定驱动滑块在Z轴上的移动范围,动平台原点的位置从bo=(0,0,175 mm)T变化到bo=(0,0,240 mm)T时,2R3T_PM并联机器人姿态工作空间逐渐变大。在位置bo=(0,0,240 mm)T时,姿态角α的变化范围是-120°~120°,β的变换范围是-180°~180°。所以,当Z取适当的位置时,2R3T_PM并联机器人可以实现大范围的转动,甚至姿态角β在理论上可以实现360°的旋转,克服了并联机器人转动工作空间小的缺点。 (a)z=175 mm (b) z=200 mm 4.2奇异性分析 由速度分析可知,该机构的速度映射包含式(7)和式(21)所示的两部分。其中,式(21)中的奇异可以很容易得到,当δ=0°或δ=180°时,式(21)发生奇异。而式(7)中的奇异位形要复杂得多,根据奇异性的分类,并联机构的奇异是由式(7)中的雅可比矩阵Jp或Jx降秩而导致的。若Jp发生奇异, 称为逆运动学奇异;若Jx发生奇异,称为正运动学奇异。 4.2.1逆运动学奇异 逆运动学的奇异性很容易得出,由于Jp是对角矩阵,故若Jp降秩,则AiCi×ni·1si=0(i=1,2,3,4)或B1C1×nGi·2s1=0,即上述的三个向量都在同一平面或叉乘部分为零,则奇异发生。 显然,这些奇异位置在工作空间的边界位置上,属于边界奇异。 4.2.2正运动学奇异 由于方程detJx=0 是非常复杂的非线性方程,很难求出其解析解,故本文用矩阵Jx的条件数来判断Jx是否奇异,矩阵Jx的条件数越大,说明机构越趋于奇异位置。由于Jx既包含有移动分量,又包含有转动分量,而不同分量的度量方式不同,因此,需首先将Jx正则化,本研究采用文献[13]提出的特征长度方法。下面所使用的条件数都是通过正则化后所计算出的。 首先,分析在位置bo=(0,0,z)T(z可以取任意值)处的Jx的条件数。图6显示的是β=0,α的变化范围是-120°~120°时,条件数κ(Jx)倒数的变化曲线。从图6中可以看出1/κx存在零点,说明在该位置条件数κx无穷大,是奇异位置。为了使2R3T_PM实现大转角转动,保证在工作空间内正常运动,必须消除奇异位置,本文采用在被动关节处添加冗余驱动的方式,即将冗余驱动添加在关节B2、B3、B4上。图7显示的是添加冗余驱动后κx随α的变化曲线,可以看出,条件数κx在2.50~2.85之间,κx随α的变化曲线变化平稳,没有突变的峰值,完全消除了奇异位置。添加冗余驱动后,κx随β的变化曲线也比较平稳,如图8所示,条件数κx在3.0~3.5之间,不存在奇异位置。下面的运动性能分析都是针对添加冗余驱动后的五自由度3D打印并联机器人的。 图6 条件数倒数1/κx随α的变化曲线 图7 添加冗余驱动后条件数κx随α的变化曲线 图8 添加冗余驱动后条件数κx随β的变化曲线 4.3灵巧性分析 为了衡量3D打印机器人运动输入与输出之间的传递关系失真程度,需要对雅可比条件数进行评估[14]。雅可比条件数越大,机构输入速度变化对输出的影响越大,当雅可比条件数等于1时,机构的运动传递性能最好。用雅可比条件数评定具有纯移动或纯转动的机构的灵巧性比较合理,但对于这类既有转动又有移动的少自由度并联机器人机构,无法保证其结论的正确性。因此本文采用文献[15]提出的局部条件指标来分析。 (23) 于是改写成: (24) 其中,JV和Jω分别表示雅可比矩阵移动部分和转动部分的局部矩阵,据此可以得到矩阵JV和Jω的条件数,分别记为κJV和κJω,它们称为线速度和角速度各项同性指标,分别用来评价机器人线速度和角速度的各项同性和灵巧性,其分布结果如图9、图10所示。 (a)条件数κJV的分布 (b)条件数κJω的分布图9 条件数在x=0,y=0,z=30 mm时的分布情况 由图9、图10可以看到,在其整个工作空间内,条件数κJV和κJω是一个很小的值,变化平稳,没有突变的峰值,保证了机构在整个工作空间内具有良好的灵巧度指数。从图10中可以看到在负Y轴上具有良好的灵巧度指数,y=-50 mm时条件数κJV和κJω的最大值分别为20和3.6左右,在x取值变化范围内曲线平稳,在设计的时候考虑把2R3T_PM的初始位置定在负Y轴上,以获得更好的灵巧性。 (a)条件数κJV的分布 (b)条件数κJω的分布 (c)κJV在y=-50 mm时的分布情况 (d)κJω在y=-50 mm时的分布情况图10 条件数在α=0,β=0,z=30 m m时的分布情况 本文设计的多向3D打印机器人可以实现在已成形的零件上加工另一部分的功能。给定打印头运动轨迹,设定打印机喷头直径为5 mm,打印头移动的法线方向如图11所示。用ADAMS软件对2R3T_PM模型进行仿真,反求得各个驱动关节的位移和速度,图12为各个驱动关节的位移和速度随时间变化的曲线。为实现3D打印机器人的运动,必须对驱动关节进行协调控制。 图11 设定的打印头运动轨迹示意图 (a)驱动关节位移 (b)驱动关节速度1.驱动关节1 2.驱动关节2 3.驱动关节3 4.驱动关节4 5.驱动关节5图12 驱动关节线位移和速度随时间变化曲线 (1)本文设计的3D打印机器人2R3T_PM采用五自由度并联机构,可实现多向3D打印。 (2)2R3T_PM采用了铰接动平台,这种新型机构可以像H4和Delta机器人一样实现大范围的移动和转动,解决了一般并联机器人工作空间小,转动能力差的问题。 (3)2R3T_PM机器人在工作空间内存在奇异位置,通过添加冗余驱动的方式能很好地消除奇异位置,并且添加冗余驱动后的机器人具有良好的灵巧性。 (4)给定2R3T_PM机器人末端执行器的运动轨迹,通过仿真求得了各个输入关节的位移和运动速度,为实现机器人控制提供参考。 [1]胡迪·利普森,梅尔芭·库曼.3D打印从想象到现实[M]. 赛迪研究专家组,译.北京:中信出版社,2013. [2]JohannesG,EmanuelP,MichaelZ.Powder-bed-based3D-printingofFunctionIntegratedParts[J].RapidPrototyingJournal, 2015,21(2):207-215. [3]ChenY,ZhouC,LaoJ.ALayerlessAdditiveManufacturingProcessBasedonCNCAccumulation[J].RapidPrototypingJournal, 2011, 17(3): 218-227. [4]ZhaoXuejin,PanYayue,ZhouChi.AnIntegratedCNCAccumulationSystemforAutomaticBuilding-around-inserts[J].JournalofManufacturing,2013,15(4):432-443. [5]SinghP,MoonY,DuttaD,etal.DesignofaCustomizedMulti-directionalLayeredDepositionSystemBasedonPartGeometry[C]//AnnualSolidFreeformFabricationSymposium.Austin,TX,USA,2003: 4-6. [6]LeeW,WeiC,ChungSC.DevelopmentofaHybridRapidPrototypingSystemUsingLow-costFusedDepositionModelingandFive-axisMachining[J].JournalofMaterialsProcessingTechnology, 2014, 214(11): 2366-2374. [7]KeatingS,OxmanN.CompoundFabrication:aMulti-functionalRoboticPlatformforDigitalDesignandFabrication[J].RoboticsandComputer-integratedManufacturing, 2013,29(6):439-448. [8]DanielG,BastianH,FranzJG.Continuous3D-printingforAdditiveManufacturing[J].RapidPrototyingJournal,2014,20(4): 320-327. [9]SongXuan,PanYayue,ChenYong.DevelopmentofaLow-costParallelKinematicMachineforMultidirectionalAdditiveManufacturing[J].JournalofManufacturingScienceandEngineering—TransactionoftheASME,2015,137(2):021005. [10]方斌,李剑锋,卿建喜,等.同构支链H4并联机构的奇异性分析[J].机械工程学报,2010,46(21):42-47. FangBin,LiJianfeng,QingJianxi,etal.SingularityAnalysisoftheH4ParallelMechanismswithIsomorphicSub-chains[J].JournalofMechanicalEngineering, 2010, 46(21):42-47. [11]Gallardo-AlvaradoJ,Ramírez-AgundisA,Rojas-GarduoH,etal.KinematicsofanAsymmetricalThree-leggedParallelManipulatorbyMeansoftheScrewTheory[J].MechanismandMachineTheory, 2010, 45(7): 1013-1023. [12]GosselinC,AngelesJ.SingularityAnalysisofClosed-loopKinematicChains[J].IEEETransactiononRoboticsandAutomation,1990,6(3):281-290. [13]ZanganehKE,AngelesJ.KinematicIsotropyandtheOptimumDesignofParallelManipulators[J].TheInternationalJournalofRoboticsResearch, 1997, 16(2): 185-197. [14]于靖军,刘辛军,丁希仑,等.机器人机构学的数学基础[M].北京:机械工业出版社,2008. [15]刘辛军.并联机器人机构尺寸与性能关系分析及其设计理论研究[D].秦皇岛:燕山大学,1999. (编辑袁兴玲) Design and Analysis of Five DOF 3D Printing Parallel Robot Pan YingFang YuefaWang Congzhe Beijing Jiaotong University,Beijing,100044 The design of a novel parallel mechanism for multi-directional 3D printing with five DOF including three translational DOF and two rotational DOF was presented. Its characteristic was that the machine adopted a articulated moving platform to achieve larger workspace. According to the established kinematics model, the inverse kinematics was calculated, the position workspace and the orientation workspace were analyzed, and the velocity Jacobian matrix was established based on screw theory. Kinematic performances, such as singularity and dexterity were analyzed based on the computed Jacobian, the motion simulation was also analyzed. The results show that the 3D printing parallel robot has larger position workspace and the orientation workspace. Although singular location existed, it might be eliminated by means of actuation redundancy and the results prove that the mechanism has better dexterity and is suitable for multi-directional 3D printing. multi-directional 3D printing; parallel mechanism; larger workspace; singularity; actuation redundancy 2015-08-22 国家自然科学基金资助项目(51175029);北京市自然科学基金资助项目(3132019) TH112 10.3969/j.issn.1004-132X.2016.17.001 潘英,女,1992年生。北京交通大学机械与电子控制工程学院硕士研究生。主要研究方向为并联机构运动学、动力学及控制。方跃法,男,1958年生。北京交通大学机械与电子控制工程学院教授、博士研究生导师。汪丛哲,男,1985年生。北京交通大学机械与电子控制工程学院博士研究生。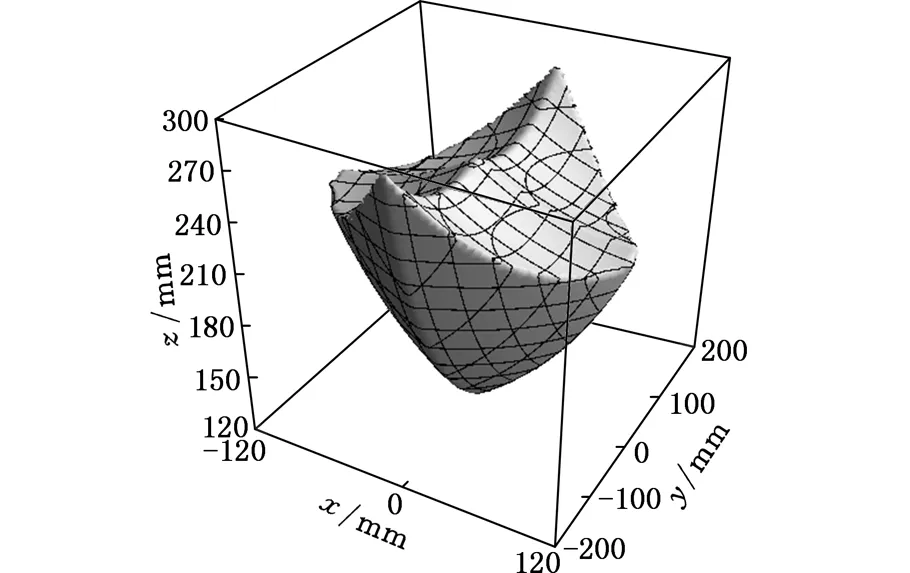
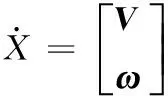
5 运动仿真分析
6 结论

