基于自然统计特征分布的无参考图像质量评价
陈 勇 帅 锋 樊 强
基于自然统计特征分布的无参考图像质量评价
陈 勇*帅 锋 樊 强
(重庆邮电大学工业物联网与网络化控制教育部重点实验室 重庆 400065)
针对目前的无参考评价方法无法准确反映人类对图像质量的视觉感知效果,该文提出一种基于自然统计特征分布(DIstribution Characteristics of Natural statistics, DICN)的无参考图像质量评价方法。其原理是用小波变换将图像分解为低频子带和高频子带部分,再将高频子带部分分成的小块,提取每一子块的幅值和信息熵,并分别计算其分布直方图均值和斜度作为特征,利用支持向量回归思想对特征进行训练,建立5种不同失真类型的质量预测模型。在此基础上,采用支持向量机针对图像特征构造分类器并进行失真判断以确定不同失真的权重,结合5种失真评价模型可得到自然统计特征分布的无参考评价模型。实验结果分析表明,该算法的评价效果优于现有的经典算法,与主观评价具有较好一致性,能够准确反映人类对图像质量的视觉感知效果。
无参考图像质量评价;小波分解;局部幅值;局部熵
1 引言
数字图像在处理、传输和存储过程中会产生不同类型、不同程度的失真,严重影响人们对图像信息的提取与理解。因此在图像采集、传输、复原、增强、检索、识别等应用领域建立有效的图像质量评价机制至关重要[1]。
自然场景统计(Natural Scene Statistics, NSS)是对自然图像具有的某种属性的统计分析,可以用来测量退化所造成的图像自然属性的破坏[2],作为图像基本成分广泛应用于通用型无参考评价算法中。而小波变换具有多尺度特性,经小波变换处理的图像可以较好地模拟人类视觉系统的多分辨率特性,成为无参考评价算法常用的图像处理方法。文献[3]采用回归模型估算质量,提出了基于两阶段框架的通用型无参考质量评价方法(Blind Image Quality Indices, BIQI);文献[4]在文献[3]的基础上通过计算影响图像质量的各种失真类型的概率来反映对图像质量产生的影响程度,提出了基于失真识别的图像保真度与完整性评价指标(Distortion Identification-based Image Verity and INtegrity Evaluation index, DIIVINE);文献[5]采用小波分解的方法,并计算子带中的幅值、方差以及信息熵的均值来构建字典,对测试图像的特征进行稀疏编码,提出了基于自然场景统计的稀疏表示(Sparse Representation of Natural Scene Statistics, SRNSS) 的盲图像评价模型;文献[6]根据经小波分解的子带能量在对数域的线性分布规律,通过量化失真图像预测值与实际值之间的能量差异来表征图像质量。同时其他的尺度变换方法也相继采用,文献[7]引入了局部DCT变换系数统计的广义参数化模型来预测图像质量得分,提出了基于离散余弦变换统计模型的盲图像质量评价(DCT Statistics Model-Based Blind Image Quality Assessment),并命名为BLIINDS-II算法;文献[8]采用拟合的高斯分布模型参数作为NR特征用于图像失真程度的描述,提出一种时域图像质量无参考评价算法(Blind/ Referenceless Image Spatial QUality Evaluator, BRISQUE);在文献[8]基础上,文献[9]采用由“自然属性”的偏离程度来度量图像的失真程度,提出了一种自然图像质量评价方法(Natural Image Quality Evaluator, NIQE)。综上所述,利用图像自然统计特性来建立质量评价模型,已经取得了较好的评价效果,但仍难以比拟全参考评价模型[10],与人类视觉的主观一致性还存在一定差距。
本文研究发现自然图像在不同的失真情况下局部幅值和局部熵的分布趋势具有一定的规律性,采用小波变换将图像分解到不同频率特性的子带空间,提取高频子带每个子块的局部幅值和局部熵,分析其直方图变化规律,并通过支持向量机[11]训练建立评价模型;然后基于支持向量机的分类原理对失真图像的失真类型进行判断并确定不同类型的权值,提出基于自然统计特征分布(DIstribution Characteristics of Natural, DICN)的无参考图像质量评价方法。在LIVE数据库[12]上实验,证明了本文的特征提取和学习方法的合理性,并且预测分数与主观分数具有很好的一致性。
2 自然统计特征的提取与分析
失真对图像自然属性影响可以表现为图像特征的变化。因此提取既能反映不同失真的差异又能反映对图像的影响程度的失真特征是关键。局部幅值反映图像子带的频率分布,局部熵反映图像某一区域的信息量的多少[13]。文献[14]认为信息熵能够有效地测量图像的信息,通过对图像信息熵直方图和图像矩阵的分析发现信息熵能够跨尺度地反应图像的统计学信息。但仅仅是信息熵无法完全体现图像质量变化的全部规律。而图像局部幅值可以反映图像子带的频率分布,因此本文将其作为对信息熵的补充。由于小波变换具有多尺度特性,经其变换处理的图像可以较好地模拟人类视觉系统的多分辨率特性。图1所示本文通过小波变换分解输入图像产生的1个低频子带和6个高频子带,进而提取在高频子带的局部幅值和局部熵。

图1 小波二阶分解示意图
为建立图像小波域局部幅值、局部熵与图像质量的关系,分别对JPEG压缩失真、JPEG2000压缩失真、快速衰落(Fastfading)失真、高斯模糊(Gblur)失真以及加性白噪声(WN) 5种情况下的小波域局部熵和局部幅值的变化情况进行分析。在文献[14]的基础上针对LIVE库中上述5种失真类型的953幅图像进行研究发现局部幅值、局部熵的分布所对应不同失真类型具一定规律。图2从LIVE图像库中选取一组图像进行自然统计特征的提取与分析为例进行说明。首先选取一组JPEG压缩失真图像,其中图2(a)为原始图像,图2(b)-图2(d)为失真程度依次递增的3幅图(注:根据数据库主观评价值(DMOS)进行选取)。

图2 JPEG失真图像
采用小波将图2中所示的4幅图像进行分解,并分别计算图像的高频子带局部幅值和局部熵,然后将局部幅值和局部熵分别按照从小到大排列并构造直方图如图3,其中图3(a)为局部幅值分布直方图,横坐标为高频子带CH的局部幅值的分布范围,纵坐标为局部幅值所占百分比;图3(b)为局部熵分布直方图,横坐标是高频子带CH的局部熵的分布范围,纵坐标是局部熵所占百分比。由图3(a)分析可知,随着失真程度的增加,局部幅值直方图分布逐渐向左倾斜,同时趋向平缓;如图3(b)所示局部熵直方图分布向左斜且逐渐平缓,分布范围也越来越分散。

图3 JPEG失真图像局部特征直方图
从LIVE图像库中分别选取与图2相同的原始图片及其4种不同类型失真的4组图片(注:省略图片),采用上述相同方法得到的局部幅值和局部熵的分布的直方图如图4-图7所示。随着JPEG2000失真程度的增加,图像的局部幅值直方图逐渐向左平移,图像的局部熵直方图逐渐向右偏斜,且分布越来越平缓如图4所示。

图4 JPEG2000失真图像局部特征直方图

图5 Fastfading失真图像局部特征直方图

图6 Gblur失真图像局部特征直方图
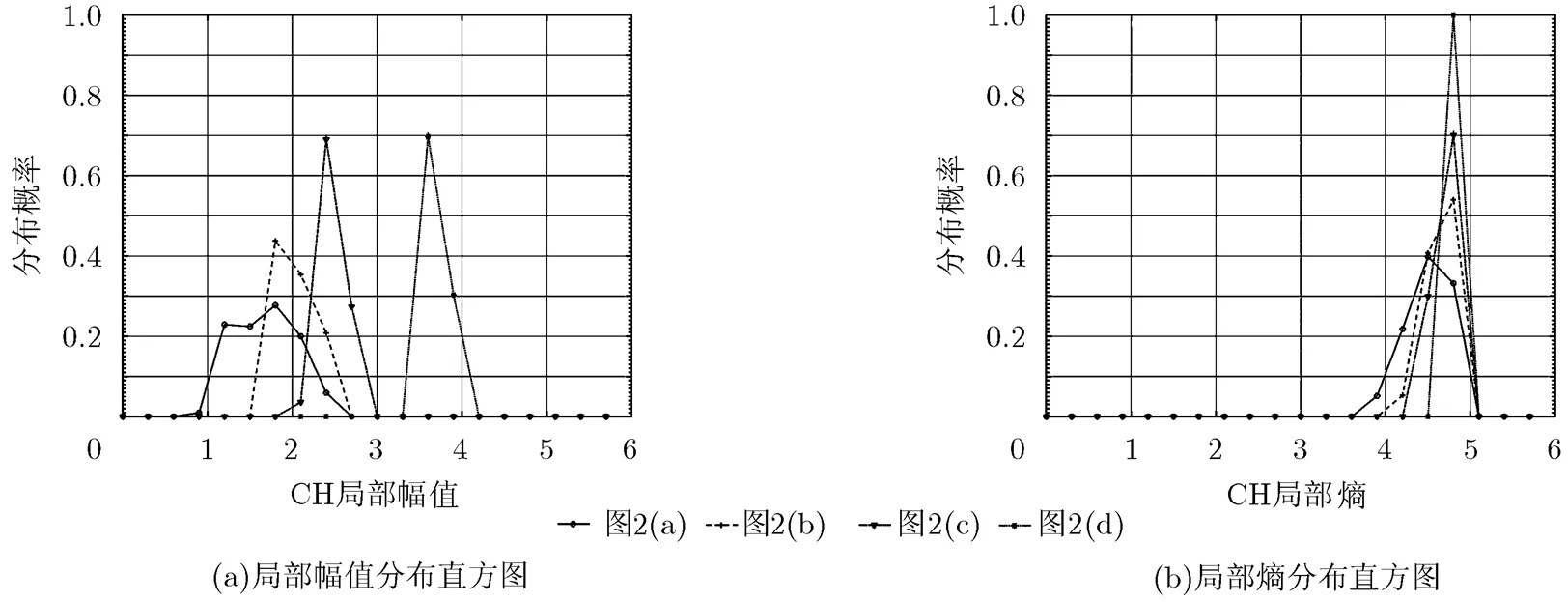
图7 WN失真图像局部特征直方图
随着自然图像快速衰落失真程度的增加,由图5可知图像的局部幅值直方图逐渐向左平移,且分布范围逐渐集中;图像的局部熵直方图则向右侧倾斜,而在倾斜过程中整体变化趋势趋于陡峭。
图6表明,随着自然图像高斯模糊程度的增加,图像的局部幅值直方图逐渐向左侧倾斜,且左侧变化逐渐陡峭,右侧部分变化不大;图像的局部熵直方图向右侧倾斜,同时随着失真程度的增加,图像的左右两侧倾斜角度大小逐渐相同。
然而对WN失真图像由图7可以看出,随着自然图像噪声含量的增加,图像的局部幅值直方图逐渐向右侧移动,且在移动的过程中变化逐渐陡峭;图像的局部熵直方图随着失真程度的增加逐渐陡峭且集中。
综上所述,自然图像在同种类型不同程度的失真情况下局部幅值和局部熵的分布具有一定的规律性,随着失真程度的加剧,自然图像的局部幅值和局部熵分布所构成的直方图会发生不同程度、不同方向的平移或倾斜;然而不同失真类型,其局部幅值与局部熵的分布有所不同。对此,将图像的局部幅值和局部熵按照从小到大进行排列,分别构造和两组数据集:
由于图像的局部幅值和局部熵分布主要集中在中间区域,从数据集和中提取位于中间区域的60%的总数据进行分析,均值和偏斜度数据集分别为
3 基于支持向量回归的图像质量预测与分类
将支持向量回归(Support Vector Regression, SVR)[15]的思想应用到图像质量的分类预测中,并选用基于支持向量机(SVM)的综合性的软件库LIBSVM[16]训练、建立质量预测模型与失真分类器。
3.1 图像质量预测模型
由上述分析可知,自然图像在不同的失真情况下局部幅值和局部熵的分布趋势都有一定的规律性,为此,针对自然图像常见的5种失真类型分别训练,提取训练样本的自然统计特征,再与图像的主观评价值构成训练集:
设定一个线性回归函数
通过求解上述模型即可得到回归方程:
3.2 图像失真分类器
提取不同失真图像的特征可以得到不同的评价模型。对未知失真类型的图像进行评价,需要构造失真分类器以判断图像的失真类型。将训练样本分为常见的5类,分别设置不同的标签。JPEG的标签; JPEG2000的标签;快速衰落的标签;高斯模糊的标签;加性白噪声的标签。提取训练样本的自然统计特征值及其对应的标签构造训练集:
根据待测图像的输入特征,通过式(22)即可输出待测图像在5种不同失真类型下的权重,由预测模型与失真分类器组建待测图像的无参考质量评价模型:
4 实验结果与分析
4.1 一致性实验
本文选择LIVE图像库进行训练与测试。LIVE图像库包含29幅高分辨率的自然图像,自然图像经过5种常见的失真处理得到5个失真图像库。在建立模型时,随机选取每一个失真图像库中70%的图像作为训练样本,其余作为测试样本。采用所提评价模型分别对5个失真子库进行客观评价,得到图8(a)-图8(e)的5幅拟合图,其中图8(f)则是所有失真图像的综合拟合图。图中横坐标是DICN的客观评价值,纵坐标是失真图像的主观评价值,每个点代表一幅测试图像。散点图越集中、拟合曲线线性度越好,则表示客观评价结果与主观感知的一致性越好。选用Pearson线性相关系数(LCC), Spearman等级相关系数(SROCC), Kendell等级相关系数(KROCC),均方根误差(RMSE)和平均绝对误差(MAE)等评价指标对所提算法的性能进行客观评估,其中LCC, SROCC, KROCC的值越接近1,图像质量越好;RMSE, MAE的值越小,主观一致性越高。LIVE数据库上各失真类型的质量评价结果如表1所示。

图8 失真图像的客观评价值与DMOS的拟合曲线
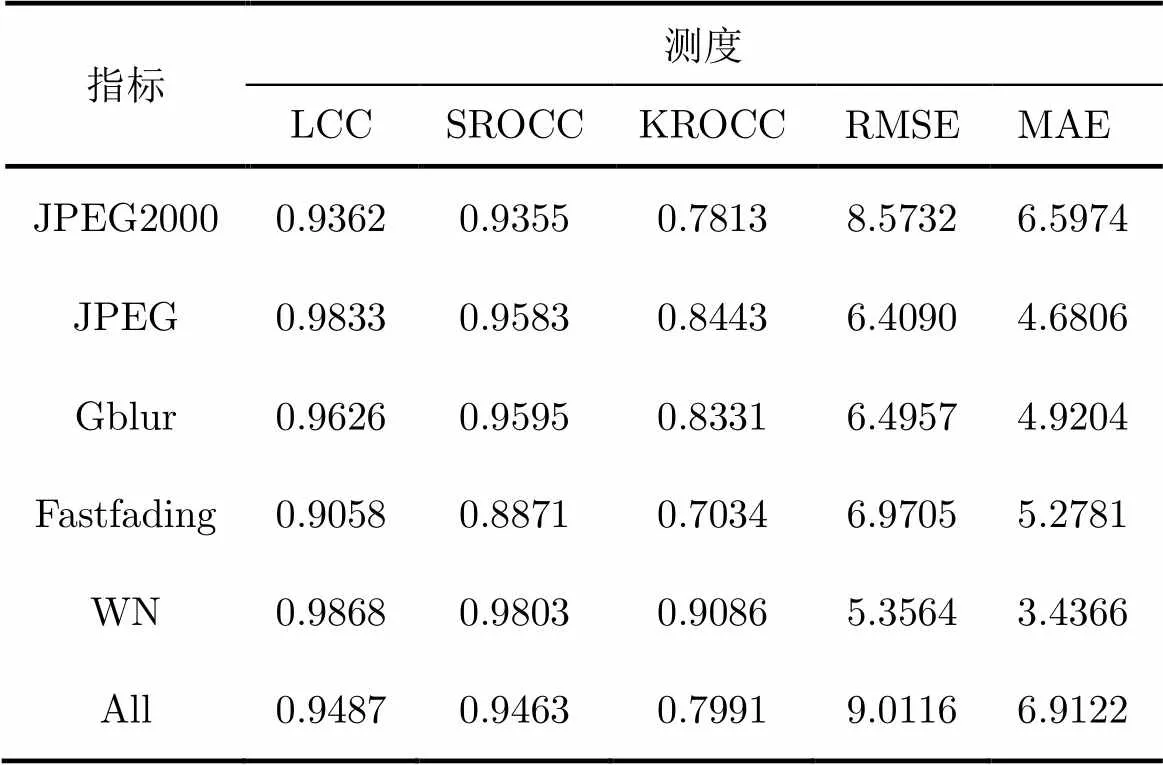
表1 LIVE数据库上各失真类型的质量评价性能
根据图8(a)-图8(e)的拟合结果和表1的质量评价性能分析,客观评价结果与主观感知具有一致性,其中WN失真类型的拟合效果线性度最好,但Fastfading失真类型的拟合效果不太理想。根据2.2节的失真图像局部特征直方图分布情况, Fastfading失真图像的局部幅值和局部熵直方图的变化虽有一定的规律但并不显著,而WN失真图像的局部幅值和局部熵直方图则有着非常明显的变化规律,本文提取的特征虽然在针对某类失真时有一定局限性,但总体对常见失真的评价效果与主观感知的一致性相吻合, 即预测分数与主观分数具有很好的一致性。
4.2 客观对比实验
本文选择反映客观评价方法精度的Pearson线性相关系数(LCC)和反映单调性的Spearman等级相关系数(SROCC)两个指标,验证算法的精度和单调性。PSNR, IFC[19], VIF[20], BIQI[3], DIIVINE[4], BLIINDS-II[5], SRNSS[6], BRISQUR[7], NIQE[8]等作为对比算法。其中,PSNR, IFC和VIF为全参考评价方法;而BIQI, DIIVINE, BLIINDS-II,BRISQUR, SRNSS和NIQE为具有代表性的无参考评价方法。测试图来自LIVE图像库。其评价结果分别如表2,表3。

表2 LIVE数据库上质量评价性能指标LCC对比
由表2和表3中的数据分析可知,相比于无参考评价方法(如BIQI, DIIVINE, BLIINDS-II, BRISQUR, SRNSS和NIQE),本文算法的综合评价性能最优;相比于全参考评价方法(如PSNR, SSIM, IFC和VIF),本文算法的综合性能仅略低于信息保真度准则方法VIF,而要优于其他全参考评价方法。视觉信息保真度(VIF)是一种基于自然场景统计模型(NSS)在进行图像质量评价时,要以使用“基准”或“完美”的图像作为参考的相似性或者保真度为前提,其实际的应用就会受到一定的制约。因此本文算法的实际应用价值更高。
4.3 算法复杂度分析
算法复杂度实验验证:测试试验平台:英特尔酷睿T9600处理器,2.8 GHz主频,4 GB内存,WIN10专业版操作系统,Matlab2015a仿真软件。由表4可以看出,本文算法的时间复杂度远远小于DIIVINE, BLIINDS-II等经典算法,稍大于BRISQUR算法,虽然与PSNR算法还有一定差距,由表2和表3中的数据可知本文算法的精确度却比PSNR算法高。本文算法仅提取图像信息熵和幅值的直方图的偏斜度与均值作为特征,因此特征量少,降低了计算的复杂度,减少了处理时间。

表4 算法运行时间测试(s/图像)
5 结论
本文提出了一种基于自然统计的无参考图像质量评价方法(DICN)。首先,通过小波变换将图像转换到小波域,对高频子带图像进行分块并提取各图像块的幅值和熵,根据图像的局部幅值以及局部熵在不同失真条件下的直方图的分布规律提取图像的自然统计特征。然后,采用支持向量回归的学习方法对5种失真图像库中的图像进行训练得到在这5种失真条件下图像的自然统计特征与图像的质量之间的映射关系。最后,通过支持向量机分类方法将上述5种失真映射模型与图像的客观质量之间的映射关系相结合建立图像的最终评价模型。实验结果表明,本文方法(DICN)与人类主观感知具有较好的一致性,证明是一种有效的无参考图像质量评价方法。
[1] REDZUAN A M and LING Shao. Non-distortion-specific no-reference image quality assessment: a survey[J]., 2015, 301(4): 141-160. doi: 10.1016/ j.ins.2014.12.055.
[2] 贾惠珍, 孙权森, 王同罕. 结合感知特征和自然场景统计的无参考图像质量评价[J]. 中国图象图形学报, 2014, 19(6): 859-867. doi: 10.11834/jig.20140606.
JIA Huizhen, SUN Quansen, and WANG Tonghan. Blind image quality assessment based on perceptual features and natural scene statistics[J]., 2014, 19(6): 859-867. doi: 10.11834/jig.20140606.
[3] MOORTHY A K and BOVIK A C. A two-step framework for constructing blind image quality indices[J]., 2010, 17(5): 513-516. doi: 10.1109/LSP. 2010.2043888.
[4] MOORTHY A K and BOVIK A C. Blind image quality assessment: From natural scene statistics to perceptual quality[J]., 2011, 20(12): 3350-3364. doi: 10.1109/TIP.2011.2147325.
[5] HE L, TAO D, LI X,. Sparse representation for blind image quality assessment[C]. 25th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Rhode Island, 2012: 1146-1153. doi: 10.1109/CVPR.2012.6247795.
[6] 金波, 李朝锋, 吴小俊. 结合NSS和小波变换的无参考图像质量评价[J]. 中国图象图形学报, 2012, 17(1): 33-39.
JIN Bo, LI Chaofeng, and WU Xiaojun. No-reference image quality assessment based on natural scene statistics and wavelet[J]., 2012, 17(1): 33-39.
[7] SAAD M A, BOVIK A C, and CHARRIER C. DCT statistics model-based blind image quality assessment[C]. IEEE International Conference on Image Processing, Brussels, Belgium, 2011: 3093-3096. doi: 10.1109/ICIP.2011.6116319.
[8] MITTAL A, MOORTHY A K, and BOVIK A C. No-reference image quality assessment in the spatial domain [J]., 2012, 21(12): 4695-4708. doi: 10.1109/TIP.2012.2214050.
[9] MITTAL A, SOUNDARARAN R, and BOVIK A C. Making a “completely blind” image quality analyzer[J]., 2013, 20(3): 209-212. doi: 10.1109/ LSP.2012.2227726.
[10] 蒋刚毅, 黄大江, 王旭, 等. 图像质量评价方法研究进展[J]. 电子与信息学报, 2010, 32(1): 219-226. doi: 10.3724/SP.J. 1146.2009.00091.
JIANG Gangyi, HUANG Dajiang, and WANG Xu,. Overview on image quality assessment methods[J].&, 2010, 32(1): 219-226. doi: 10.3724/SP.J.1146.2009.00091.
[11] VAPNIK V N. An overview of statistical learning theory [J]., 1999, 10(5): 988-999. doi: 10.1109/72.788640.
[12] SHEIKH H R, WANG Z, CORMACKL,LIVE image quality assessment database, Version 2[OL]. http://live.ece. utexas.edu/research/quality,2014.
[13] 付晓薇, 代芸, 陈黎, 等. 基于局部熵的量子衍生医学超声图像去斑[J]. 电子与信息学报, 2015, 37(3): 560-566. doi: 10. 11999/JEIT140587.
FU Xiaowei, DAI Yun, CHEN Li,. Quantum-inspired despeckling of medical ultrasound images based on local entropy[J].&, 2015, 37(3): 560-566. doi: 10.11999/JEIT140587.
[14] LIU Lixiong, LIU Bao, HUANG Hua,No-reference image quality assessment based on spatial and spectral entropies[J].:, 2014, 29(8): 856-863. doi: 10.1016/j.image. 2014.06.006.
[15] SCHÖLKOPF B, SMOLA A J, WILLIAMSON R C,. New support vector algorithms[J]., 2000, 12(5): 1207-1245. doi: 10.1162/089976600300015565.
[16] CHANG C C and LIN C J. LIBSVM: A library for support vector machines, Version 3.20[OL]. http://www. csie.ntu.edu. tw/~cjlin/libsvm/index.html,2014.
[18] 张继红, 郑俊生. 多元再生核径向基函数研究[J]. 大连交通大学学报, 2015, 36(1): 109-117. doi: 10.13291/j.cnki.djdxac. 2015.01.029.
ZHANG Jihong and ZHENG Junsheng. Study of multivariate reproducing kernel radial basis function[J].,2015, 36(1): 109-117. doi: 10.13291/ j.cnki.djdxac.2015.01.029.
[19] SHEIKH H R and BOVIK A C. Image information and visual quality[J]., 2006, 15(2): 430-444. doi: 10.1109/TIP.2005.859378.
[20] SHEIKH H R, BOVIK A C, and DE VECIANA G. An information fidelity criterion for image quality assessment using natural scene statistics[J]., 2005, 14(12): 2117-2128. doi: 10.1109/TIP.2005. 859389.
A No-reference Image Quality Assessment Based on Distribution Characteristics of Natural Statistics
CHEN Yong SHUAI Feng FAN Qiang
(&,,,400065,)
The current No-Reference Image Quality Assessment (NR-IQA) methods are not well consistent with subjective evaluation, a novel NR-IQA method based on the DIstribution Characteristics of Natural statistics (DICN) is proposed in this paper. In the proposed method, image is decomposed into low frequency subbands and high frequency subbands with wavelet, and its high frequency subbands are divided into blocks at size of 8×8, their amplitude and entropy are respectively extracted from the blocks, then their mean values of the distribution histogram and skewness are respectively calculated, and their results are as the image features. The features trained by Support Vector Regression (SVR) are for building 5 kinds of distortion image quality pre-measurement model. To determine the weights of the different distortions, the image features of classifier based on SVR are structured for carrying out the distortion evalution. Based on 5 kinds of distortion evaluation models, the NR-IQA model with the natural statistical distribution can be obtained. The results of experiments show that the proposed method performance is better than the present classical methods. The method is well consistent with the subjective assessment results, and can reflect human subjective feeling well.
No-Reference Image Quality Assessment (NR-IQA); Wavelet decomposition; Local amplitude; Local entropy
TP391
A
1009-5896(2016)07-1645-09
10.11999/JEIT151058
2015-09-14;改回日期:2016-01-20;网络出版:2016-03-14
陈勇 chenyong@cqupt.edu.cn
国家自然科学基金(60975008),重庆市教委科学技术研究项目(KJ1400434)
The National Natural Science Foundation of China (60975008), Science and Technology Research Project of Chongqing Education Committee (KJ1400434)
陈 勇: 男,1963年生,教授,研究方向为图像处理与模式识别.
帅 锋: 男,1990年生,硕士生,研究方向为图像处理.
樊 强: 男,1989年生,硕士,研究方向为图像处理.

