一种基于梯度方向一致性的边缘检测新算法
李 正 张 海
一种基于梯度方向一致性的边缘检测新算法
李 正*张 海
(北京航空航天大学飞行器控制一体化技术重点实验室 北京 100191)
为达到同时提取图像的主要边缘和微弱边缘并有效抑制噪声的目的,该文利用真实图像边缘两侧的灰度渐变性,以及边缘点周围灰度梯度的方向一致性好而非边缘点周围灰度梯度的方向一致性差的特点构造了梯度方向和(SGD)指标;并根据该指标提出一种阈值自适应的边缘检测算法。实验表明:梯度方向和在有效提取边缘点的同时能较好地抑制高强噪声;该指标对光照和对比度变化有较强的鲁棒性;将其用于阈值的自适应调节,得到的基于梯度方向一致性的边缘检测方法能较好地解决兼顾弱边缘检测的同时而不引入噪声干扰的问题。
边缘检测;梯度方向;一致性;抗噪;自适应阈值
1 引言
边缘检测是图像处理的基本问题,在图像分割、特征提取、视觉导航等领域有广泛的应用[1,2]。基于微分的边缘检测算法如Sobel算子、Prewitt算子、Laplace 算子和Canny[3,4]算子等,因计算高效而被广泛应用。在Canny算子的基础上,研究者们做了一些有意义的改进。文献[5]设计了一种基于统计特性的贝叶斯方法;文献[6]先用ADM空域算子计算初始边缘图,再利用改进的极大值抑制算法获得最终边缘,也取得了较好结果。在Canny构架的启发下,很多研究者构造了一些新型卷积核用来检测边缘。比如文献[7]提出了一个新的尺度归一化方法,并构造了尺度不变的边缘检测算法。文献[8]结合一个各向同性的小尺度高斯核和一个各向异性的大尺度高斯核,获得了一种抗噪边缘检测算法。
然而微分算子对噪声、光照变化、对比度变化等因素极为敏感[9],虽然人们进行了一些改进,但仍没有较好地解决这个问题。文献[13,14]从频率域的角度出发,提出了相位一致性的概念。相位一致性不受灰度梯度的影响,所以能较好地抵抗光照变化与对比度变化。基于文献[13,14]的工作,文献[15]改善了计算相位一致性的能量函数模型,文献[16]提出了一种单演信号[17]相位一致性(Monogenic Phase Congruency, MPC)模型,取得了较好的边缘检测效果。但是此类算法一方面计算量很大,很难应用于实时系统,另一方面对于大尺度模糊边缘不敏感,所以没有得到广泛的应用。
事实上空间域也存在一致性现象,即局部区域内的梯度方向一致性。文献[18]最早将局部边缘一致性的概念应用于边缘检测算法的评估,但该方法依赖于阈值筛选以后的结果,所以无法独立完成边缘检测任务。文献[19]则将梯度方向进行编组,进而提出了一种直线检测算法;文献[20]在该算法的基础上,利用梯度方向的编组信息构造梯度方向的显著度描述,并将其作为蚁群算法的启发信息,从而构造了基于蚁群优化的边缘检测算法。
本文提出一种新的能够有效量化描述边缘附近像素灰度梯度变化的梯度方向一致性算子,并在此基础上设计了自适应边缘检测算法,利用梯度方向一致性信息同时实现结构化微弱边缘提取、噪声干扰压制,实验验证算法具有良好的边缘检测性能。
2 梯度方向一致性与梯度方向和算子
自然图像的边缘往往是具有多像素宽度的灰度过渡带[21]。过渡带内图像灰度的变化通常会具有明显的规律性,称为梯度方向一致性,与边缘的可能性密切相关。为利用其完成自适应边缘检测,本文设计了可定量描述此规律性的灰度梯度方向和算子。
2.1 灰度梯度方向和的定义
图1(a)是一个含0.1%椒盐噪声的竖直边缘图,图1(b)为边缘区的局部放大,从图1(b)的灰度信息可以看出,灰度梯度方向具有一致性。

图1 梯度方向和的构造过程
以水平方向为例分析该一致性,图1(c),图1(d)分别为区域ABCD内的灰度及其水平方梯度值,梯度计算方法如式(1):
由图1(b),图1(d)可见:除噪声点外,梯度变化具有明显的规律性。但梯度值对光照、对比度、噪声等十分敏感,这也正是基于梯度的边缘检测方法面对的主要问题。
为去除灰度梯度波动影响,建立该一致性与边缘存在可能性间鲁棒的映射关系,本文使用式(2)对灰度梯度进行量化描述,以灰度梯度是否沿给定方向代替其绝对值,给定点(,)处水平方向梯度方向计算公式为
其中,为确定是否存在梯度方向的判定阈值,经式(2)处理后,ABCD区域内给定像素点沿水平方向的梯度方向如图1(e)所示。
图1(e)能够有效隔离灰度梯度变化的影响,揭示边缘附近的灰度变化规律,但信息尚不便于被有效利用,为此进一步设计了3×3邻域灰度梯度方向和,简称梯度方向和(Summation of Gradient Direction, SGD)指标。水平方向()处SGD值定义为
以上研究的是水平方向的梯度方向和计算方法,竖直方向以及倾斜45º方向的情况可依此类推获得。
2.2 合成梯度方向和(ISGD)
由式(3)可知SGD的值域为[-9,9],因值域较小不利于边缘处一致性的细化分析。同时当检测方向与实际边缘有夹角情况下,以45º角为例,水平与竖直两个正交方向均会获得相同的SGD值,不利于边缘方向的有效区分。为此进一步设计了合成梯度方向和(Integrated Summation of Gradient Direction, ISGD)指标。
式(4),式(5)给出了水平方向与竖直方向的ISGD计算方法,其中,,,分别为右上、右下、左下方向的梯度方向和。如图2所示,,为采用相邻正交方向SGD合成的水平、竖直方向SGD值。
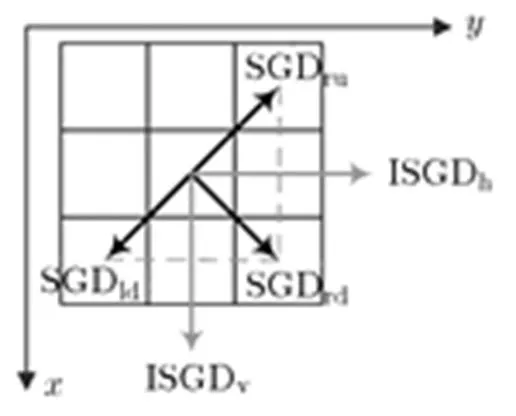
图2 合成梯度方向和
由式(4),式(5)可见,ISGD将SGD的值域范围扩大为[-18, 18],可更好地支持后续边缘区域一致性细化分类;同时通过有效处理,相对SGD能够提高边缘方向的角度分辨率,具体方法如2.3节中所述。
2.3 合成梯度方向和的运用
由SGD的定义可见其计算的是给定方向的一致性,实际图像中边缘会有各种不同的方向,为简化计算,选取以下8个方向进行SGD值计算,然后进行合成处理。
图3中给出了SGD的8个计算方向,利用相邻的两个正交方向SGD值,能够获得8个不同方向的ISGD值。以沿竖直方向的边缘为例,由方向2、方向8的SGD合成的沿方向1的ISGD会明显高于沿方向2或沿方向8的ISGD,因此对边缘方向的角度分辨率相对SGD提高了1倍。

图3 8个方向的SGD
对于边缘的存在性,仅考虑ISGD的绝对值即可,式(6)给出用于边缘存在性判定的ISGD计算方法:
表1为几种用于边缘检测的指标对比,各指标被映射到0~255灰度级。原图中将图像的一半进行亮度与对比度的调整。从表中可以看出:Canny梯度与文献[8]梯度对亮度和对比度变化敏感,亮度低的区域梯度值明显低,这在传统的边缘检测算法中很容易导致漏检测;相位一致性指标[15]虽然具有抗光照与对比度变化的能力,但在粗边缘渐变区会出现非常明显的丢失现象,这是因为相位一致性检测的是阶跃型边缘,对于缓慢变化的斜坡形边缘则很难检测到,比如Lena头像中左侧的木架子在梯度图与梯度方向一致性图中能明显反映出来,而在相位一致性图中则被完全漏检;此外相位一致性容易出现“毛刺”,如Photography图像中右下部的草地等;相比而言,ISGD指标能突出地显示完整的边缘,尤其对灰度渐变型的边缘和弱边缘有很好的指示作用,而且ISGD指标与梯度幅值没有明显关系,具有很强的鲁棒性。但是从表1中也可以看出,ISGD显示的是边缘过渡区的情况,所以轮廓粗,不能直接作为最终的边缘检测结果。
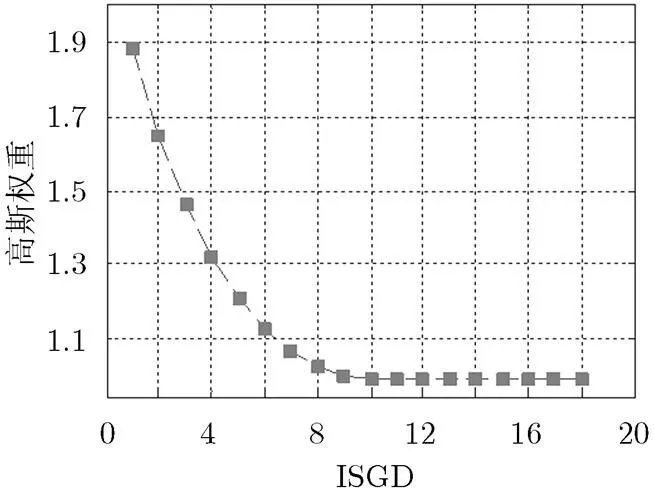
图 4 以ISGD为变量的高斯权重
3 基于SGD/ISGD的边缘检测算法
如表1最后一列所示,ISGD值已经与边缘建立了良好的对应关系,但由于ISGD指标描述的是边缘过渡区域内的一致性,不利于边缘的精确定位,需要结合具体梯度幅值进行更精确的定位。本文采用梯度阈值的方法获得边缘,SGD/ISGD作为辅助指标对梯度阈值进行自适应调节。
传统的边缘检测算法通常只关注强边缘,而忽略灰度变化不明显的弱边缘。但弱边缘也往往含有重要的结构信息,比如表1的Lena图像中Lena背后的木架。对于此类边缘,Canny等传统的边缘检测算法需要将阈值设置较低,但随之会引入噪声干扰,而基于相位一致性的边缘检测算法则可能会产生漏检(如表1中第1行第4列所示)。为解决这个问题,本文一方面根据梯度分布情况将边缘分为强边缘与弱边缘两类,相应地梯度阈值也分为高低两类;另一方面,每一类阈值在其基础阈值之上根据ISGD进行自适应调节。

3.1 基础阈值的确定
以像素()为中心,观察窗口长度为范围内所有像素点的梯度幅值。如果水平或竖直方向上连续有个点的梯度幅值小于梯度阈值T,则判定该点属于弱边缘候选区P。其中,的取值与边缘区域的宽度有关,本文强调真实图像的边缘是一条灰度过渡带,宽度通常在3个像素以上,考虑到有些弱边缘模糊程度大,应该取更大的值。通过大量实验可以发现,取5时对弱边缘的检测效果较好。T是区分边缘强弱的阈值,其取值与观察者的个体差异有关,本文为了简化处理,将T设置为固定值,该值通过大量实验获得,本文的经验值为10。
P中的基础阈值T()取低基础阈值FL(),非P中取高基础阈值FH(),即
低基础阈值FL与T以及3.2节中的高斯权重有关。3.2节中提到的自适应阈值由基础阈值乘以高斯权重获得,由图4可知,高斯权重的最大值接近整数2,而弱边缘的梯度幅值小于T,所以低基础阈值取值为T/2,即为5。高基础阈值FH通过统计平均获得,其计算方法具体如下:
首先,以()为中心的×的邻域内,对方向一致性好的点进行统计,并求出它们的梯度均值(,)。计算公式如式(8):
式(8)中,P(,)为×的邻域内大于6的点的集合,取6的目的是去除图1所示噪声点的影响,表示集合中元素个数,为梯度幅值。
其次,为保证不被非边缘区域拉低,将标识弱边缘的阈值T作为最小门限,高基础阈值始终不能低于此门限。最终高基础阈值的选取为
某一像素是边缘点的可能性与该像素的ISGD呈正相关。基于此,本文中利用ISGD对3.1节中的基础阈值进行高斯加权,如图4所示,ISGD越小,权重越高,反之则越低。加权根据ISGD采用高斯分布与均匀分布相结合的方式,在ISGD小于时按照高斯分布计算权重,在ISGD大于时权重为1。
权重计算为
式中是高斯分布的均值,也是均匀分布的取值,为高斯分布的标准差。
均值的取值与梯度方向和的分布特点有关。由图1(f)可知,即便没有噪声点的干扰,边缘区中的SGD也不完全相同,靠近边界的点为6,中心点为9。而这些点是边缘点的可能性却是相同的,所以SGD在6以上的点的高斯权重可以设置为1。反映在以合成梯度方向和(ISGD)为变量的高斯权重上,均值应设置为12。但是从本文提出的整体算法来看,由于3.3节中的进一步调节,导致一些含噪声的边缘被漏检,所以真实的均值比理论值12要略小,实验表明取10效果较好。标准差的取值与图像的信噪比有关,信噪比高的图像可适当缩小,本文取经验值8。
为进一步去除非边缘特征点的影响,本文对ISGD指标进行规律化统计。在以边缘点为中心的统计区域内,ISGD值的分布比较集中且都比较高,所以大于高值h的个数与大于低值l的个数相差不大。以非边缘点为中心的统计区域,ISGD分布规律性差,所以ISGD值分布分散,大于h的点的个数比较少,而大于l的点的个数相对多。根据此特性,将统计区域内ISGD大于h的像素点数量与大于l的像素点数量之比叫做ISGD的降速比,用I表示。R越大,说明该像素点是边缘的可能性越大,反之则越小。文中h取12,l取6,原因在于12反映的是图1(f)中边界处的ISGD, 6反映的是噪声点和非边缘点的ISGD。
本文的统计区域取21×21,将R映射到[0,18]区间内,采用2.2节中的的权重调节策略,获得关于降速比的阈值调节权重W:
3.4 算法流程
步骤1 设置用于计算ISGD的阈值,计算8个方向的梯度方向和,并确定每个像素点的S;
步骤2 计算Canny梯度(这里也可以选取其他常用梯度,如Sobel梯度等),并进行非极大值抑制,将非极大值抑制确定的点集作为初始边缘点集。这里需要指出的是,非极大值抑制仅与局部区域内像素点的相对灰度关系有关,与具体的梯度幅值无关;
步骤3 用Canny梯度确定P;
步骤4 确定基础阈值;
步骤5 计算与ISGD相关的权重W;
步骤6 计算与ISGD的规律性相关的权重W;
步骤7 基础阈值乘以权重,进行阈值的自适应调节,并确定最终的边缘图。
4 实验
实验在i5-2400 处理器、主频3.1 GHz、内存4 GB 和MALTAB 2014a 平台上进行,分别与Canny梯度、文献[8]、Kovesi相位一致性[15]等方法进行实验对比。各方法的参数在程序默认值的基础上进行微调,以达到最佳效果为准:文献[8]中各向异性的大尺度高斯核=4,滤波器个数=16; Kovesi相位一致性程序中,LogGabor小波的尺度为4,方向参数为6。
4.1 抗噪性能及弱边缘检测效果对比
为了客观地评价本文算法的抗噪性与保留弱边缘的能力,选用了一张合成图进行测试。图中包含一条竖直边缘和水平边缘,水平边缘将合成图分为上下两部分,上半部分中的边缘对比显著,下半部分的边缘对比微弱。在图中分别添加零均值、标准方差为5,10,15,20的高斯白噪声,如表2中的第1列所示。表2中第2至第4列分别为Canny算子、文献[8]、Kovesi的相位一致性[15]对应的边缘检测结果,最后一列为本文结果。
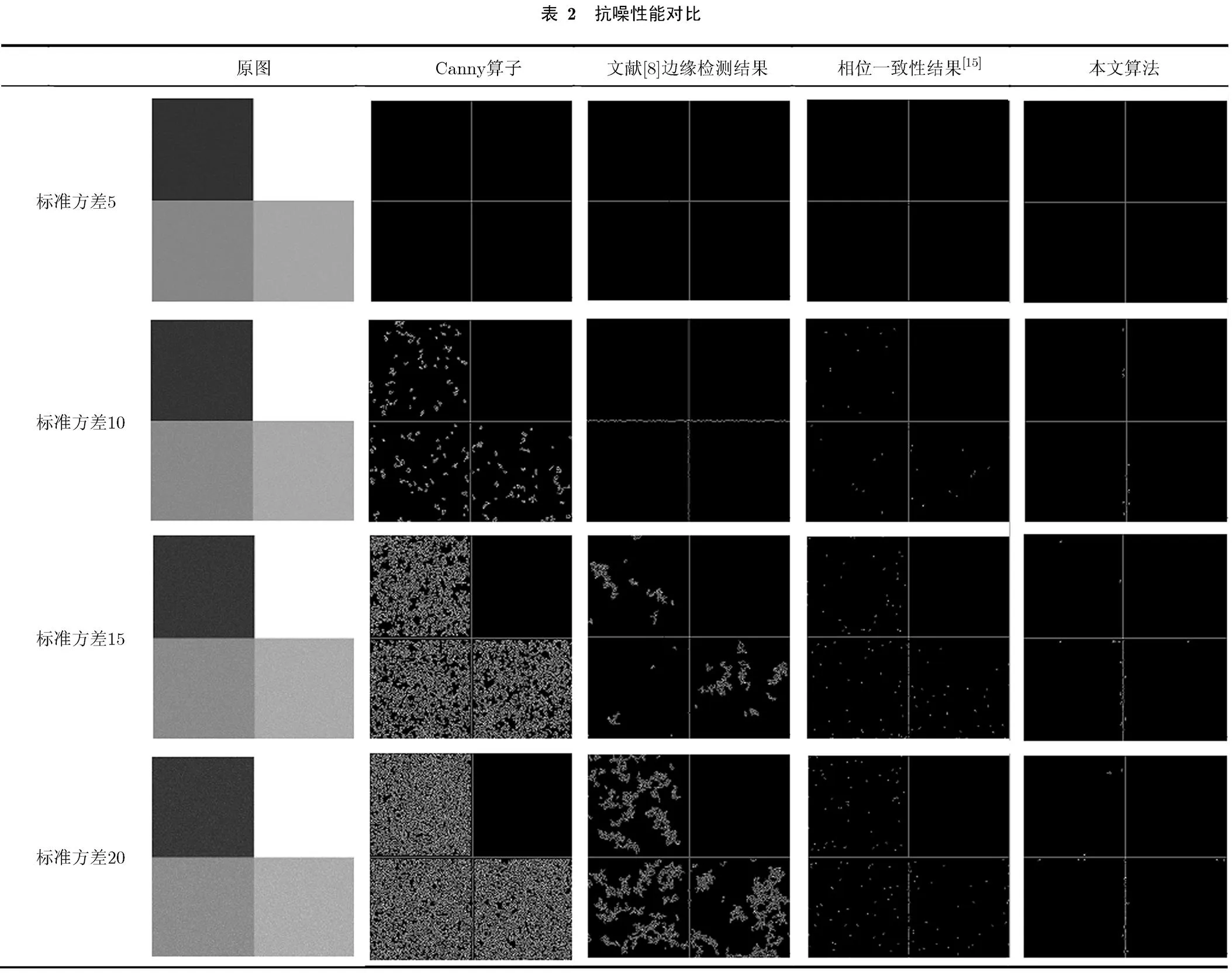
在抗噪性方面:由于Canny的阈值是固定的,所以随着噪声的增强,边缘图明显包含越来越多的噪声点;文献[8]提供的方法具有良好的抗噪性,但需要设置合适的尺度,尺度越大抗噪性越好,由于尺度设置较大,所以在噪声强度较弱时,检测到的边缘有变形的趋势,如第3列第2行、第3行所示;相位一致性和本文算法有更强的抗噪性。
在检测弱边缘方面:虽然Canny算子与文献[8]算法能检测到弱边缘,但不能同时兼顾抗噪性;相位一致性虽然有较好的抗噪性,但在弱边缘检测方面出现了断断续续的漏检情况,如第4列第4行所示;本文算法能较好地解决检测弱边缘而不引入噪声干扰的问题。
4.2 FOM品质因数评价
为了对不同算法进行更综合的定量比较,本文用FOM品质因数指标进行评估,其定义为
式中,N为Ground Truth(GT)理想边缘图中边缘点的个数,N为算法检测到的边缘点的个数。d为检测到的像素点到GT图中的最短距离,为调节系数,取常值0.25。
测试图为南佛罗里达大学[22]提供的经典图集。测试方法:在原图统一加入标准差为10的零均值高斯白噪声,计算边缘图与GT图的FOM品质因数。结果显示本文算法在总体上表现最优。部分测试结果如表3所示。
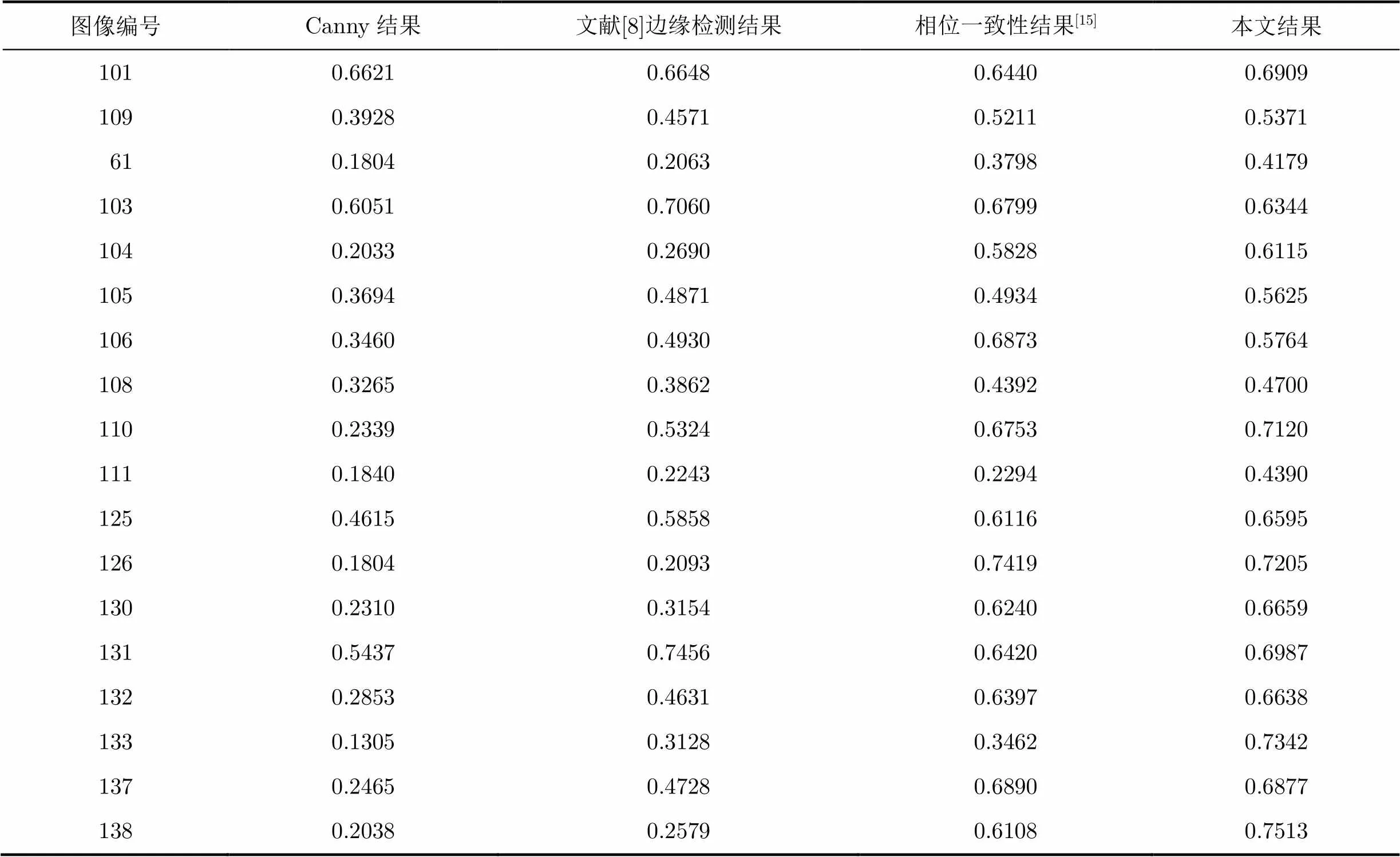
表3 FOM品质因数评估
由FOM的定义可以看出,FOM值越大,则边缘检测结果越接近理想GT图。总体来看,本文算法要优于其他算法。其中103和131的检测结果中,文献[8]提供的算法最优,106, 126, 137的检测结果中,基于相位一致性的算法最优。但从FOM的具体值可以看出,当本文算法不是最优结果时,与其他算法的差距并不大。
4.3 实例
最后本文结合3个典型实例,通过具体的检测效果对不同算法进行对比。首先对表1中的Lena图与Photography图进行对比实验,为了综合比较不同算法在抗噪性、抗光照变化、抗对比度变化等方面的性能,在原图中增加标准差为10的白噪声。
此外,边缘检测算法的评估一般选取特定的图集与其对应的标准边缘图(Ground Truth)进行对比测试,但标准边缘图受绘制者主观影响较大,并且通常是轮廓图。前文已经强调,图像的弱边缘往往也包含大量反映图像特征的重要信息,这在图像匹配等方面有重要作用。第3个例子本文选择了一张典型的含有强边缘、弱边缘、非边缘干扰的沙发图(南佛罗里达大学测试图集中的109图)作为测试对象进行效果对比。
图5(a)-图5(e)是Lena图的检测结果。整体看,本文提出的算法在抗造性方面最好,虽然文献[8]算法也有较好的抗造性,但此时设置的尺度参数较大,导致一些细节边缘出现变形的现象,比如Lena的头发和帽子等。在检测弱边缘方面,由于上半部分光照弱、对比度低,所以Kovesi相位一致性算法[15]和文献[8]算法都没有把图中左侧的木架子完整地检测出来,Canny算子虽然能检测出来,但同时引入了较多的噪声。类似的还有图中其他两处被标记的地方。

图5 实例对比
5 结束语
本文根据图像边缘的梯度方向具有局部一致性的特点,构造了SGD/ISGD指标,该指标能有效反映真实图像的边缘过渡区;该指标对光照和对比度变化有很强的鲁棒性;根据SGD/ISGD指标并借鉴Canny的非极大值抑制设计了一种基于梯度方向一致性的边缘检测方法。实验表明,该方法能较好地解决边缘检测精度与抗噪声性能的协调问题;具有抗光照与对比度变化的能力;对梯度方向一致性好的微弱边缘有较好的检测效果。
[1] TSAI Piyu, CHANG C C, and HU Y C. An adaptive two-stage edge detection scheme for digital color images[J]., 2002, 8(4): 329-343. doi: 10.1006/rtim. 2001.0286.
[2] ZIOU D and TABBONE S. Edge detection techniques-an overview[J].&, 2000, 8(4): 537-559.
[3] Canny J. A computational approach to edge detection[J]., 1986, 8(6): 679-698. doi: 10.1109/TPAMI.1986. 4767851.
[4] Galvanin E A S, DO VALE G M, and DAL POZ A P. The canny detector with edge region focusing using an anisotropic diffusion process[J]., 2006, 16(4): 614-621. doi: 10.1134/S1054661806040067.
[5] Hancock E R and Kittler J. Adaptive estimation of hysteresis thresholds[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Proceedings CVPR’91), Maui, HI, USA, 1991: 196-201. doi: 10.1109/ CVPR.1991. 139687.
[6] Ray K. Unsupervised edge detection and noise detection from a single image[J]., 2013, 46(8): 2067-2077. doi: 10.1016/j.patcog.2013.01.029.
[7] ZHANG Xiaochun and LIU Chuancai. An ideal image edge detection scheme[J]., 2014, 25(4): 659-681. doi: 10.1007/s11045- 013-0224-9.
[8] SHUI P L and ZHANG W C. Noise-robust edge detector combining isotropic and anisotropic Gaussian kernels[J]., 2012, 45(2): 806-820. doi: 10.1016/ j.patcog.2011.07.020.
[9] 石美红, 李青, 赵雪青, 等. 一种基于保角相位的图像边缘检测新方法[J]. 电子与信息学报, 2015, 37(11): 2594-2600. doi: 10.11999/JEIT150364.
SHI Meihong, LI Qing, ZHAO Xueqing,. A new approach for image edge detection based on conformal phase[J].&, 2015, 37(11): 2594-2600. doi: 10.11999/JEIT150364.
[10] 许宏科, 秦严严, 陈会茹. 一种基于改进Canny的边缘检测算法[J]. 红外技术, 2014, 36(3): 210-214.
XU Hongke, QIN Yanyan, and CHEN Huiru. An improved algorithm for edge detection based on canny[J]., 2014, 36(3): 210-214.
[11] HAO Fei, SHI Jinfei, ZHANG Zhisheng,. Canny edge detection enhancement by general auto-regression model and bi-dimensional maximum conditional entropy[J]., 2014, 125(15): 3946-3953. doi: 10.1016/j.ijleo.2014.01.153.
[12] XU Qian, VARADARAJAN S, CHAKRABARTI C,. A distributed Canny edge detector: algorithm and FPGA implementation[J]., 2014, 23(7): 2944-2960. doi: 10.1109/TIP.2014.2311656.
[13] Morrone M, ROSS J, Burr D,. Mach bands are phase dependent[J]., 1986, 324(6094): 250-253.
[14] Morrone M C and Burr D C. Feature detection in human vision: A phase-dependent energy model[J].:, 1988, 235(1280): 221-245. doi: http://dx.doi.org/ 10.1098/rspb.1988.0073.
[15] Kovesi P. Image features from phase congruency[J].:, 1999, 1(3): 1-26.
[16] Wang Lijuan, Zhang Changsheng, Liu Ziyu,. Image feature detection based on phase congruency by monogenic filters[C]. 2014 26th Chinese Control and Decision Conference (CCDC 2014), Changsha, China, 2014: 2033-2038. doi: 10.1109/CCDC.2014.6852502.
[17] Felsberg M, and GERALD S. The monogenic signal[J]., 2001, 49(12): 3136-3144. doi: 10.1109/78.969520.
[18] Kitchen L and Rosenfeld A. Edge evaluation using local edge coherence[C]. Proceedings SPIE Techniques and Applications of Image Understanding, Washington, D.C., USA, 1981: 284-298. doi:10.1117/12.965757.
[19] Burns J B, Hanson A R, and Riseman E M. Extracting straight lines[J].,1986, 8(3): 425-455. doi: 10.1109/ TPAMI.1986.4767808.
[20] 张志龙, 杨卫平, 李吉成. 一种基于蚁群优化的显著边缘检测算法[J]. 电子与信息学报, 2014, 36(9): 2061-2067. doi: 10.3724/SP.J.1146.2013.01506.
ZHANG Zhilong, YANG Weiping, and LI Jicheng. A novel salient image edge detection algorithm based on ant colony optimization[J].&, 2014, 36(9): 2061-2067. doi: 10.3724/SP.J.1146. 2013.01506.
[21] 冈萨雷斯. 阮秋琦, 阮宇智. 数字图像处理第2版[M]. 北京:电子工业出版社, 2007: 464.
[22] Bowyer Kevin, Kranenburg Christine and Dougherty Sean. Edge detector evaluation using empirical ROC curves[J]., 2001, 84(1): 77-103. doi: 10.1006/cviu.2001. 0931.
An adaptive Edge Detection Approach Based on the Gradient Direction Consistency
LI Zheng ZHANG Hai
(,,100191,)
A novel mathematical index about edge detection is constructed to indicate both conspicuous edges and inconspicuous edges in a gray-level image. The index called Sum of Gradient Direction (SGD) is derived from the basic idea that the gradient directions of the points surrounding the real edge point have good consistency while the gradient directions of those surrounding the noise point have poor consistency. According to the SGD index a new adaptive thresholding method to detect edges is proposed. A great quantity of experiments show that: the SGD index has the ability to distinguish both conspicuous edge points and inconspicuous edge points from the noisy points; the proposed novel edge detector utilizing the SGD to regulate the gradient threshold has the ability of detecting weak edges and suppressing noisy points at the same time.
Edge detetion; Grident direction; Consistency; Anti-noise; Adaptive threshold
TN911.73
A
1009-5896(2016)07-1674-08
10.11999/JEIT151130
2015-10-10; 改回日期:2016-02-26;网络出版:2016-04-26
李正 bayexx@126.com
李 正: 男,1987年生,博士生,研究方向为组合导航与最优估计.
张 海: 男,1970年生,副教授,研究方向为最优估计,组合导航、智能交通等.

