关注细微之处 提升课堂实效
程佰畏
(安徽省临泉第一中学,236400)
关注细微之处提升课堂实效
程佰畏
(安徽省临泉第一中学,236400)
一、关注例题细微之处,启发思维生成
课堂教学是由无数个教与学的细节共同组成的,只有处理好每个细微的地方,才能保证课堂教学的实效性.随着新课改的不断深入,教师应该静下心来,梳理思绪、细致研究、关注细微之处,就会有更好的发现来启发学生的思维生成,优化学生的解题方法.长此以往,学生的思维能力将会得到很好的提升.


学生从习题中受到这种启发性的思维过程,通过细微之处的延伸,学生自然地加深了向量共线性定理的理解,不仅再次强化了知识点内在蕴含的结构联系,也加深了学生思维理解层面的生成,为今后有关此类问题的解决打下了基础.如果我们不在授课中培养学生对这种细微之处的观察分析,来启发学生思维的生成,以后学生在高考中出现类似的试题,有的学生就可能无法下手.所以做个有心人,在课堂细微之处多一份关注,多一点追问和思考,便不会在解题过程中因为小的细节,而错失机会.所以只有在教学中对这样的细节,有针对性的讲解,才会让我们的教学少走弯路,实现课堂教学的有效性.
二、关注习题细微之处,凝练常规思维
在实际的课堂教学中除了需要讲授新课例题之外,还需要关注学生练习中遇到的问题.如果说平时的教学是栽活一棵棵树,那么习题就是为它们浇灌,使之茁壮成长为一片林.因此,教师应通过适当的习题训练,帮助学生寻求解决一类问题的方法与策略,关注习题的细微之处,凝练学生解决常见问题的常规思维,为进一步研究相关问题打下坚实的基础,从而实现课堂教学的有效性.
例2如图2,已知∆OAB.
本研究中,西医治疗组采取西药治疗,中西医联合治疗组则采取西药加上清迈解毒饮治疗。结果显示,中西医联合治疗组效果、红斑、炎性丘疹、毛细血管扩张、脱屑消失时间、症状积分水平、生存质量水平相比较西医治疗组更好,P<0.05。中西医联合治疗组副反应和西医治疗组无明显差异,P>0.05。



解析(1)由点P在直线AB上,得
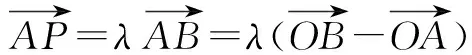
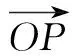


x=1-λ,y=λ,
所以x+y=(1-λ)+λ=1.
(2)由题意,可设x+y=t,t∈(0,1),则

设P′为平面内一点,且



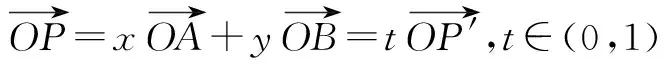
通过这样的习题,并加以细微的分析可以看出,学生在已有相关知识的基础上(比如上面的例1)加以训练,就能帮助学生在自主学习和合作探究中凝练思维.这种教学的方式不仅加深了对原有问题的理解,更重要的是在解法的探究、问题的思辩过程中,学生通过类比的常规思维而使解决新问题的能力得到培养.所以,我们在教学中要善于捕捉、恰当处理、关注习题细微之处,在探究中渗透,在巩固中提升.针对题目中解答过程出现的“似真现象”,由点及面,做到对知识精雕细琢、对思维的精心凝练.只有这样,才能真正使数学课堂走向深刻、走向实效.
三、关注考题细微之处,拓展思维广度
考题的讲评课也是课堂教学的一种不可缺少的一个重要环节,它对于查漏补缺、巩固知识、深化对知识的理解,拓展思维广度具有不可替代的作用.然而,高中数学试题的讲评课的现状不容乐观,突出表现在用力平均,针对性不强;忽视学情,就题讲题,缺乏必要的思维拓展.如何提升这类课堂教学的有效性,笔者认为,把握考题的细微之处,理清命题意图,拓展思维广度,可以让考题讲评课发挥其应有的作用,真正提高课堂教学的实效性.


当λ>0,μ>0时,P表示的区域为图3中的①;
当λ<0,μ>0时,P表示的区域为图3中的②;
当λ<0,μ<0时,P表示的区域为图3中的③;
当λ>0,μ<0时,P表示的区域为图3中的④.


由以上分析可知,该考题就是课本中例题和习题的延伸,是对例1和例2的拓展,应属于基础题.但是由于学生在平时学习中未关注细节,不熟悉教材而变成了难题,使得当年本题得分率不高.像这样考查双基的试题比比皆是,不论平时测验还是高考试题,很多题目都可以在课本中找到原题.这就为我们课堂教学提出了一个值得注意的问题,那就是关注课本中的细微之处,挖掘可探究性的问题,拓展学生的思维广度.在教学中联系课本中的例题、习题的原型,回归本源,让学生关注课本,关注基础,关注数学思想和数学方法,这样就能在高考中以不变应万变,做到处变不惊,游刃有余.
因此,我们在平时课堂教学过程中,千万不能小瞧教学中的细节,这些我们平时错失的细微之处,也许即是触摸到的高考冰山一角,但由此也就失去了大海中的整座冰山.关注细微之处,需要教师的经验和智慧,更需要我们的心细和敏锐的洞察力.教师应更多地发现学生在学习中存在的问题,进而深入思考解决问题的方法,让学生的思维走向灵活、走向深入.
总之,课堂教学的艺术在很大程度上就体现在教师敏锐地捕捉课堂教学细微之处,科学地处理有关问题.如果我们的课堂教学有更多的细微之处被教师关注,那么我们的教育就一定会变得更迷人、更有效.汪中求在《细节决定成败》一书中就说“一定要注重细节,把小事做细”.因此,关注教学的细微之处,对课堂的处理做到精雕细琢,才能真正让数学的课堂走向深刻,走向实效.

