多层次分析 全方位解题

◇　山东　孙晋山

◇　江苏　侍昌亚



多层次分析全方位解题

◇山东孙晋山

在平时的解题训练中,对一道问题进行多层次、全方位解答,能够有效拓展同学们的思维,提高分析问题与解决问题的能力．下面举例说明．

本题以三角函数为背景、分段函数为形式,给出了函数的单调性,探究参数的可能取值．问题具有一定的开放性,有利于考查同学们的发散思维.下面从多层次对问题进行分析、解答．

1　从概念出发,直接推理

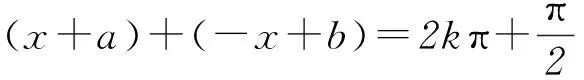
变式1函数y=sin(2x+φ)(0≤φ≤π)是R上的偶函数,则φ的值是().

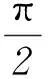
2　借助图形,直观推理

图象法能直观体现函数的相关性质,是处理函数问题的有力工具,本题可借助函数y=sinx与y=cosx图象关系求解．

在同一坐标系内作出函数y=sinx与y=cosx的图象(如图1)．

图1

2个函数图象相差π/2个单位,而y=cosx本身就是偶函数,因此问题可转化为将y=sinx平移a+b个单位即可．故选C．

变式2已知函数f(x)=|sinx|+|cosx|,现有如下几个命题:

① 该函数为偶函数;

② 该函数最小正周期为π;

其中正确命题为________.

图2

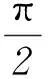
答案: ①、③、④．

3　小题小做,特值求解

变式3满足cos(α+β)=cosα+cosβ的α、β的一组值是________.(写出满足条件的一组值即可)

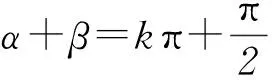
4　逐一代入,检验求解

根据选择题的特点,必有一个选项满足条件,因此可将4个选项分别代入已知函数关系式,再逐一检验,即可得出正确选项．

变式4已知函数f(x)=cosxsin 2x,下列结论中错误的是().

Ay=f(x)的图象关于点(π,0)中心对称;

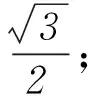
Dy=f(x)既是奇函数,又是周期函数

对于选项A,若函数关于(π,0)中心对称,则有f(π+x)+f(π-x)=0,代入检验知此式成立,所以f(x)关于点(π,0)中心对称,故选项A正确.

由正、余弦函数性质可知f(x)既是奇函数,又是周期函数,排除选项D,故选C.

综上,本文所述的综合问题,内容丰富、变形空间大,运算灵活,既有通法,也有巧法.通过对一道题从多角度进行深刻分析,把握其内部蕴含的不同知识点的本质联系,有利于培养和优化同学们解题思维.

1　巧用转化思想,优化解题

转化思想,即把问题从一种形式转化为另一种形式,从而找出问题突破口的一种数学思想方法．转化思想是数学研究中克服难关的有效手段,具有一定的灵活性和多样性,有助于发散思维,培养解题能力．

(1) 当a∥b时,求cos2x-3sin 2x的值.

(2) 求f(x)=(a+b)·b的最小正周期和单调递增区间.

2　把握特殊化思想,巧妙解题

特殊化思想是解数学选择、填空题中常用的一种思想方法,在解题过程中通过选取符合题意的特殊值、特殊位置、特殊方程、特殊图形以及特殊向量等方式,使问题化难为易、化繁为简．

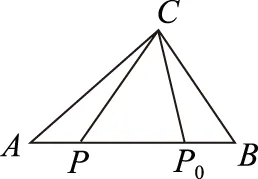
图1

AAC=BC;

B∠ABC=90°;

C∠BAC=90°;

DAB=AC

图2

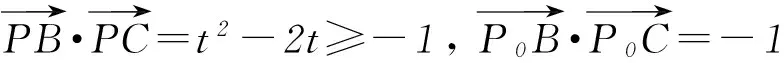
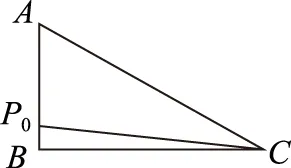
图3

同理可判断选项C、D错误.

3　注重数形结合,直观解题

数形结合思想是数学解题中常用的数学思想方法之一,融合了形象思维和抽象思维,其实质是将抽象乏味的数学语言与直观形象有机地结合起来．

|2a-b|的最大值、最小值分别是________.

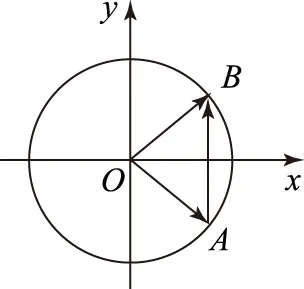
图4

(作者单位：盐城市亭湖高级中学)

山东省枣庄市第四中学)

◇江苏侍昌亚

数学思想方法是数学知识、数学思维、数学能力的本质体现．在数学解题中,缺乏数学思想方法的有效引导,解题易陷入束手无策、无从下手的局面．对此,笔者从平面向量知识点出发,略谈数学思想方法在解题中的应用,以供参考．