平面向量高考重点题型及解题策略

◇　山东　贾锡波



平面向量高考重点题型及解题策略

◇山东贾锡波

平面向量作为高中数学新增内容,在高考中一般涉及4个方面：1)通过向量的数量关系解决有关平行、垂直问题；2)通过向量的数量积关系解决有关参数求值问题；3)通过坐标法解决向量问题,即几何问题代数化；4)等价转化、函数与方程思想解决数量积最值问题．现将这些重点问题及解题策略总结如下,供同学参考使用．

1　选好基向量解决线性运算、数量积问题

A|b|=1;Ba⊥b;

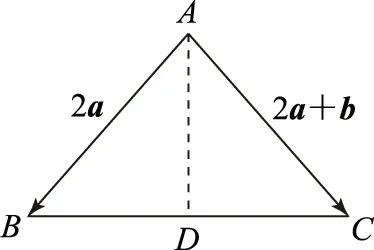
图1

故选D.

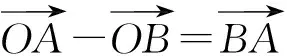
2　运用等价转化思想解决平面向量求值问题

|b|2+x2+y2-4x-5y+xy=

x2+(y-4)x-5y+|b|2=

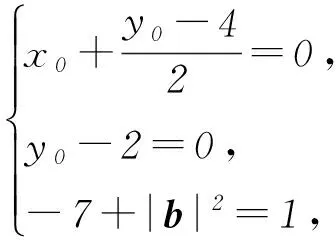
解题策略以平面向量模长为背景的函数最值问题属于较难题,首先要分析题意将问题等价转化,此题等价于“当且仅当x=x0、y=y0时|b-(xe1+ye2)|取到最小值1”,这是解决此题的关键突破口,也是最小值的本质.平方后转化为关于x、y的二元二次函数的最值求解,求解中需将其视为关于某个字母的二次函数再利用配方法．

3　几何问题用向量代数法解决

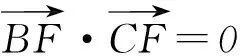
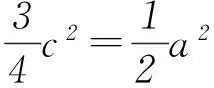
解题策略对于线线垂直问题运用向量的数量积为零即可解决．求线线角问题一般是先求2直线所在的向量,然后通过向量的夹角公式解决．2直线的平行问题是通过求2直线的向量,看是否存在相关关系．若存在,则平行．距离问题一般需要寻找过点与直线垂直向量的模,即为距离．

4　运用函数与方程思想求数量积的最值

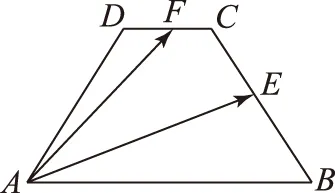
图2

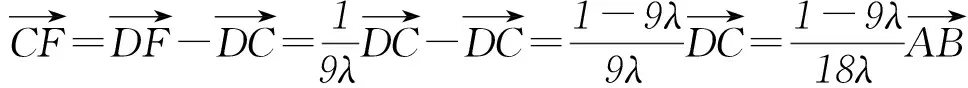
因为

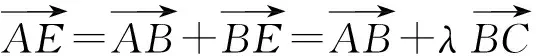
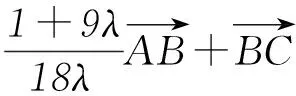
所以

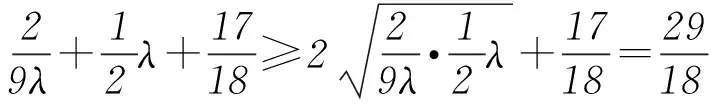
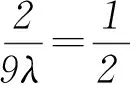
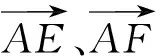
总之,平面向量是高考的重点知识,在复习中要注意常考题型的归纳，常规解题方法的总结、关注平面向量与其他知识的交会，进而提高解题效率．

山东省平度经济开发区高级中学)