受控三轴应力-应变下沉积物声速与物理力学性质的关系

龙建军，周华建，李赶先，陈聪

(1.广东工业大学 机电工程学院，广东 广州 510006；2.中国科学院 南海海洋研究所 中科院边缘海地质重点实验室，广东 广州，510301)



受控三轴应力-应变下沉积物声速与物理力学性质的关系

龙建军1，周华建1，李赶先2，陈聪1

(1.广东工业大学 机电工程学院，广东 广州 510006；2.中国科学院 南海海洋研究所 中科院边缘海地质重点实验室，广东 广州，510301)

对南海某海域深度100～400 m的海底浅层(约2 m埋深范围)沉积物柱状样在接近海底水压力下进行三轴应变-声学同步测量，结果表明沉积物纵波声速有两个特征：(1)从应变过程开始到结束，沉积物纵波声速不断变化；(2)平均声速随着平均静弹性模量的增加，由大变小又由小变大，存在声速最小值。这些结果与海底浅表层沉积物的物理力学性质、围压、颗粒的结合状态改变有关。此外，沉积物动弹性模量和孔隙度呈良好的负相关性，这与孔隙度增大含水量增大有关；动弹性模量是静弹性模量的10～100倍，这主要与三轴应变试验的应变数量级与声波振动产生的应变数量级的差异大有关。采用本论文实验测量的数据分别建立了双复合参数-声速和孔隙度-声速经验公式，分析结果表明双复合参数-声速公式声速预报误差约是孔隙度-声速公式的1/4，表明双复合参数-声速公式更加有效。

南海；海底沉积物；声速；三轴应变；经验公式

1　引言

海底是实际载体的承受界面，在海洋工程中是前期勘探对象之一。对海底沉积物力学性质的研究开始于Stoll等[1—2]。在垂直加载的受控应力-应变过程中，声速随应变增加会有不同的响应，其物理机制已经引起研究人员的注意[3—4]。海底沉积物物理性质对声速的影响，Hamilton和Bachman[5—6]、Anderson[7]和卢博等[8]学者都独立得到了海底沉积物孔隙度和颗粒度等声速的经验公式。这些结果基本没有考虑三轴应力-应变的影响，但实际海底沉积物使处于三轴应力-应变状态下的，因此本文开展垂直加载的受控三轴应力-应变过程的声学测量，探讨三轴应变下声速与物理力学性质之间关系的变化趋势；另外三轴应变-声学同步测量可以获得沉积物的体积压缩模量等数据，满足利用作者前期论文[9—10]提出的双复合参数-声速理论模型建立声速经验公式的需要，因此采用相同的实验数据分别建立双复合参数-声速和孔隙度-声速经验公式，将可探讨它们的差别。

2　实验方法和数值计算方法

2.1实验方法

本文实验研究的受控轴向应力-应变过程是加围压、不排水状态下的压缩试验，附加一对100 kHz声学换能器在被测量的沉积物试样两端，组成一个轴向应力-应变/声学测量系统；上端声学换能器增加浮力结构使其在水中成悬浮状态，避免声学换能器自重影响测试结果，见图1。测量与装置是在文献[3]的基础上改进，采用特别定制的土工三轴仪(江苏省南京土壤仪器厂造)可以准确自动加载围压、轴向压力与测量压缩变形。可加载的最大围压为2.5 MPa。声学测量系统由DB-4型声波参数测定仪和个人计算机组成，用来实现窄脉冲声波的发射和接收，进行信号放大、数据采集和数据储存。

为模拟沉积物海底承载过程，本试验选择不固结不排水剪切的UU试验方法，用三轴试验测定土的强度参数。样品的安装和剪切试验过程按国家土工试验方法标准[12]要求进行。

根据沉积物取样时站位水深及试验条件，试验所用三级围压分别为300 kPa、500 kPa、700 kPa。样品初始直径68 mm，经过削土后的试样直径为38 mm，高度125 mm，高度与直径之比为2.0～3.5。

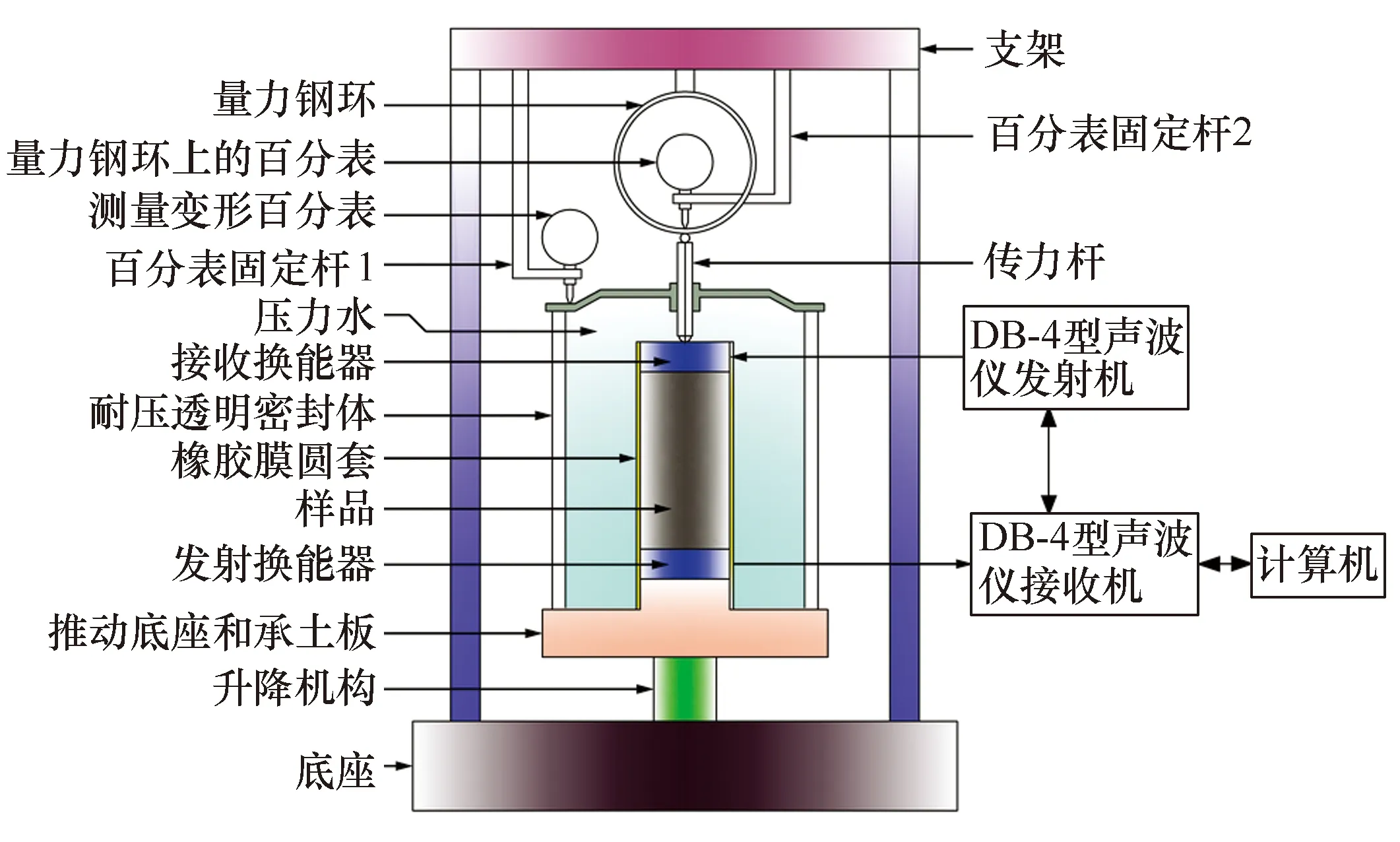
图1　三轴应力-应变/声学测量系统Fig.1　Schematic diagram of acoustic measurement system in controlled three axis stress-strain

试验所用剪切应变速率取0.9 mm/min。试验时每产生0.5 mm变形值，记录一次测力计读数和轴向变形值，同时测量一次声波走时和声波首波幅值，测量过程由计算机自动记录数据。当测力计读数达到稳定或出现倒退时，本级围压下的剪切试验结束。换试样按相同的方法进行第二级、第三级围压下的剪切试验。

2.2数值计算方法

沉积物声波速度为：

(1)

式中，l为不断受压的样品的高度，单位：mm，该高度在应变过程中是不断变化的；t为声波通过试样的走时，单位：μs。

试样的轴向变形、校正面积和轴向应力计算采用土工三轴仪制造公司提供的软件自动完成。

由于部分试样为水饱和的黏性土，在实测时，试样的高度和直径均有稍微变化，但在允许范围之内。

2.3实验样品的制备

沉积物样品来自南海某海域大陆架。由于海底沉积物的物理力学性质与岩石和泥岩截然不同，特别是在抵抗单轴应力的应变过程中，抗剪强度比岩石和泥岩要低很多[13]。经初步试验发现，海底沉积物样品不适合做单一试样的多级加荷试验。根据试验标准，把沉积物试验样品分为6组，每组3个样品，共18个样品。每一组样品中的3个沉积物试验样品均取自同一海域，海底埋深相近，物理性质相似。

表1是6组样品沉积的物理参数、站位水深及试验围压。

表1　试验样品分组编号、物理性质、站位水深及试验围压

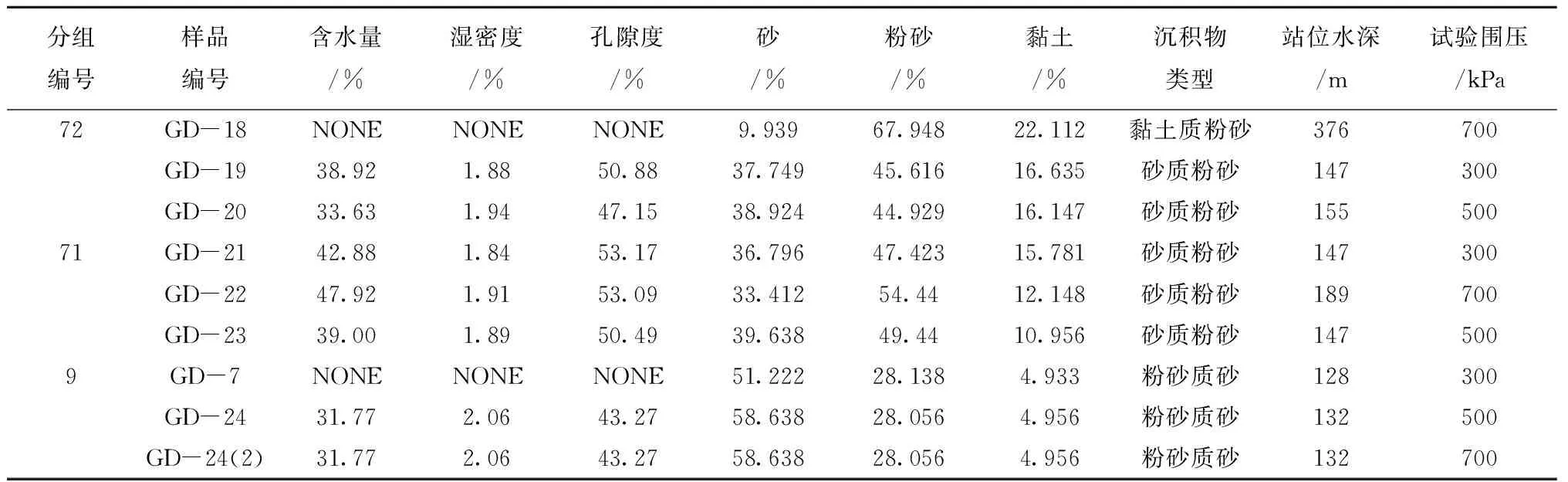
续表1

注：NONE表示没有获得该项实验数据的可靠值。

2.4声速测量数据预处理

三轴试验过程中的声速测量是在轴向压缩条件下进行的，样品的长度不断地缩短，声速也在不断地变化。如样品GD-10的声速变化曲线见图2。

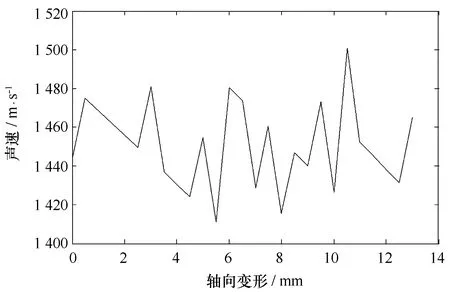
图2　样品GD-10的声速变化曲线Fig.2　Velocity curve of sample GD-10 sediments with deformation

把整个压缩过程中的声速取平均值，各组沉积物样品在剪切压缩过程中的平均声速见表2。

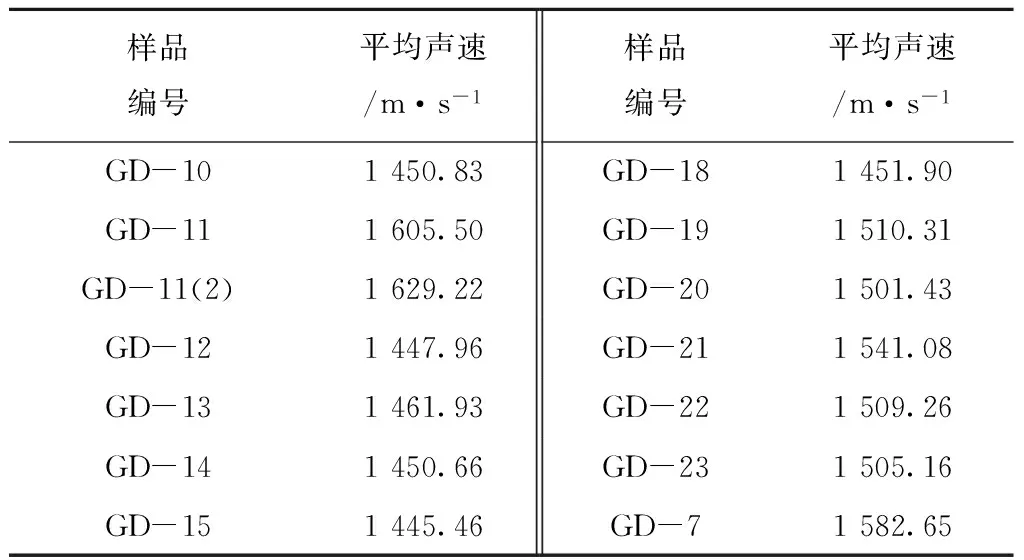
表2　沉积物样品平均声速

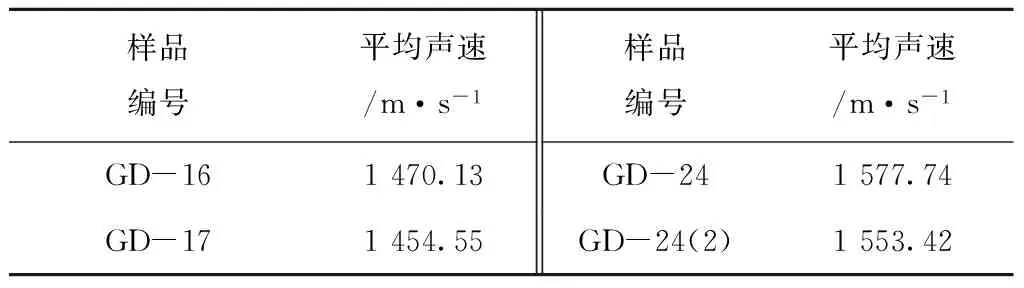
续表2

3　实验结果和分析

3.1动弹性模量与声速关系分析

在声波幅度较小时，平面纵波波速公式为：

(2)

式中，M为等效弹性模量。M=K+4/3 μ，K、μ和ρ分别为介质的体积模量、切变模量和密度。

在三轴试验的压缩过程中，通过声学测量得到沉积物样品在不同压缩阶段的声速数据。然后根据式(2)得到沉积物在三轴压缩变形过程中的动弹性模量M。表3为各沉积物样品的平均动弹性模量。

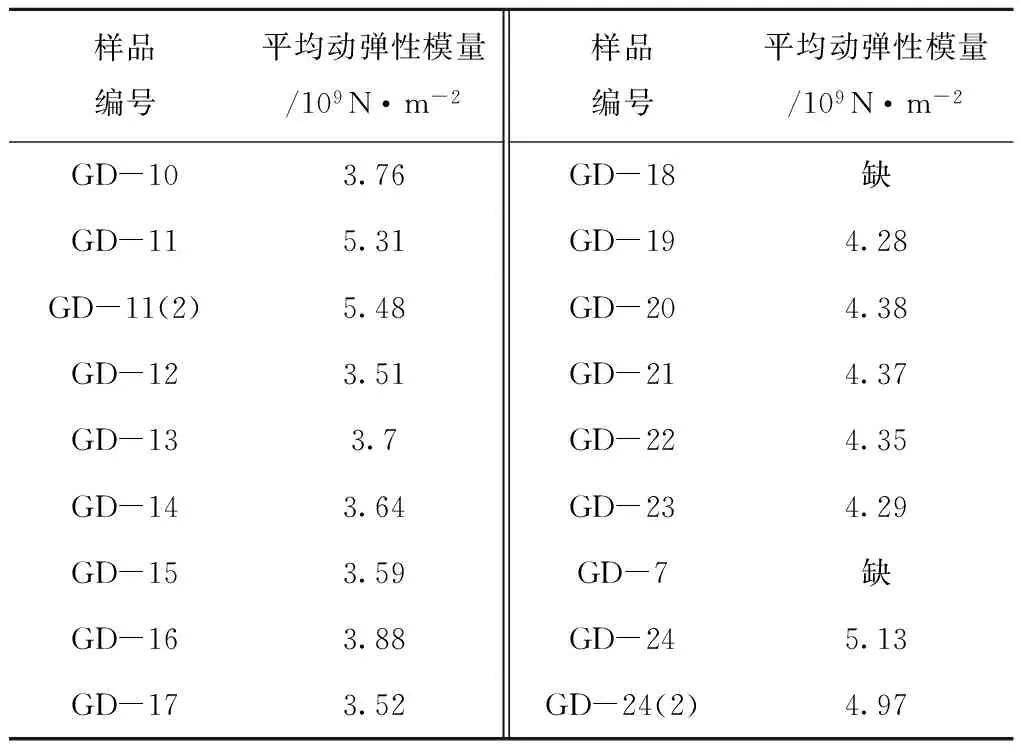
表3　各沉积物样品的平均动弹性模量

以沉积物样品的孔隙度和平均动弹性模量进行回归分析，得到拟合曲线，见图3。

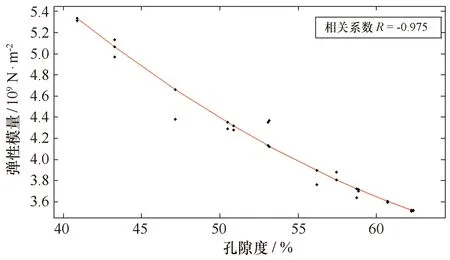
图3　沉积物孔隙度与动弹性模量关系Fig.3　Relationship between the porosity and the dynamic modulus of the sediments

由图3可知，沉积物的孔隙度和动弹性模量呈良好的负相关关系，这与Hamilton[14]的结果一致。

3.2静弹性模量与声速关系分析

在三轴试验中，主应力差σ1-σ3为已知测量值。试样为圆柱体时泊松比ν表示为：

(3)

式中，ε3为侧向应变，ε1为轴向应变。

沉积物样品的体积应变εv为：

(4)

根据三轴试验原理[11]，沉积物样品在不同压缩阶段的静弹性模量为:

(5)

应用Hamilton的结果[15]，沉积物的站位水深对应的泊松比如表4。

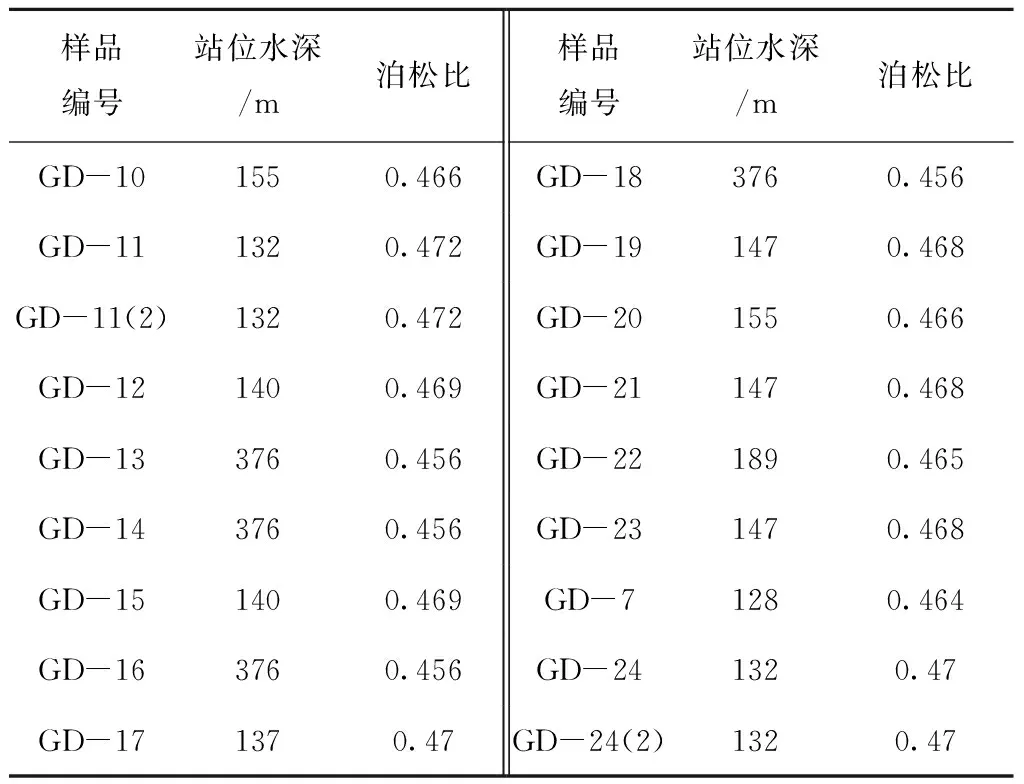
表4　沉积物水深及泊松比

由式(5)可知，沉积物静弹性模量随着压缩过程中应变的增大而减小，且不同围压σ3对沉积物静弹性模量影响较大。联立式(3)～(5)可以计算出沉积物样品在三轴压缩过程对应的静弹性模量E。

以下分别对不同围压、不同轴向变形的静弹性模量E进行对比分析。沉积物在轴向压缩过程中，静弹性模量是不断地变化的，故取各沉积物样品的平均静弹性模量与孔隙度进行数据拟合。图4a～c为不同围压下沉积物静弹性模量与孔隙度关系。

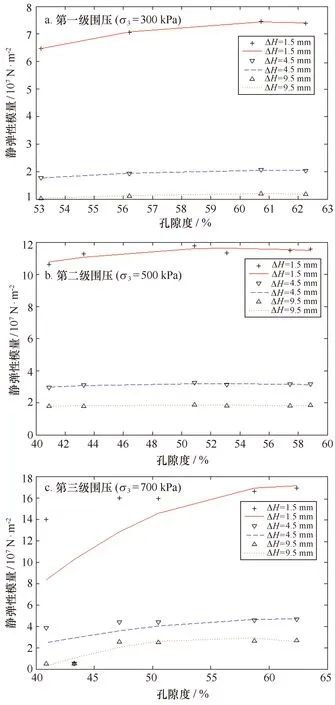
图4　不同轴向变形下静弹性模量与孔隙度关系Fig.4　Relationship between the static elastic modulus and the porosity under different axial deformation

由图4a～c可知，在围压相同时，沉积物在不同的轴向变形下静弹性模量值有明显的差异，且静弹性模量随孔隙度的增加呈增大的趋势。其主要原因是饱和沉积物刚性与含水量密切相关。

平均静弹性模量和平均声速的相关性曲线，见图5。由图5可知，沉积物的声速先随着静弹性模量的增大而减小，在静弹性模量4×107～5×107N/m2之间声速取得最小值，尔后声速随着静弹性模量的增大迅速增大。

图5　沉积物静弹性模量与声速关系Fig.5　Relationship between the static elastic modulus and the acoustic velocity of the sediments

通过对比发现动弹性模量是静弹性模量的10～100倍。与Mavko等[16]的结果比对，本文的动、静弹性模量值在合理区间内，它们数量级差异也与Mavko Gary的结果一致。

作者前期论文[9—10]已经提出了双复合参数-声速理论模型，三轴应变-声学同步测量可以获得沉积物的体压缩模量等数据，满足建立双复合参数-声速经验公式的需要，第4节对此加以讨论。

4　海底沉积物双复合参数-声速经验公式

4.1固结等效弹性模量和固结密度计算

饱和海底沉积物湿密度[9]ρn为:

(6)

式中，n、ρw分别为孔隙度和海水的密度，ρs表示排水固结后砂、粉砂、黏土3种成分组成的沉积物的密度。

排水固结后以砂、粉砂、黏土组成的沉积物等效弹性模量[9]Ms为：

(7)

式中，M1、M2、M3分别表示沉积物的砂、粉砂、黏土的等效弹性模量，θ1、θ2、θ3分别表示砂、粉砂、黏土的体积分数。

各成分的体积分数和质量分数可以通过以下理论关系换算：

(8)

式中，参数R1、R2、R3分别表示表示砂、粉砂、黏土的质量分数，ρs1、ρs2、ρs3分别表示表示砂、粉砂、黏土的矿物颗粒密度。

砂、粉砂、黏土的等效弹性模量和矿物颗粒密度参考Hamilton[14]给出的大陆台阶(大陆架和大陆坡)沉积物对应参数的计算值。各参数通过单位换算后的数值如表5。

表5　沉积物3种成分的等效弹性模量和颗粒密度

联立式(6)～(8)可以计算出本实验所用的各海底沉积物的固结密度ρs和固结等效弹性模量Ms，其结果如表6(数据缺失或重复样品未列出)。

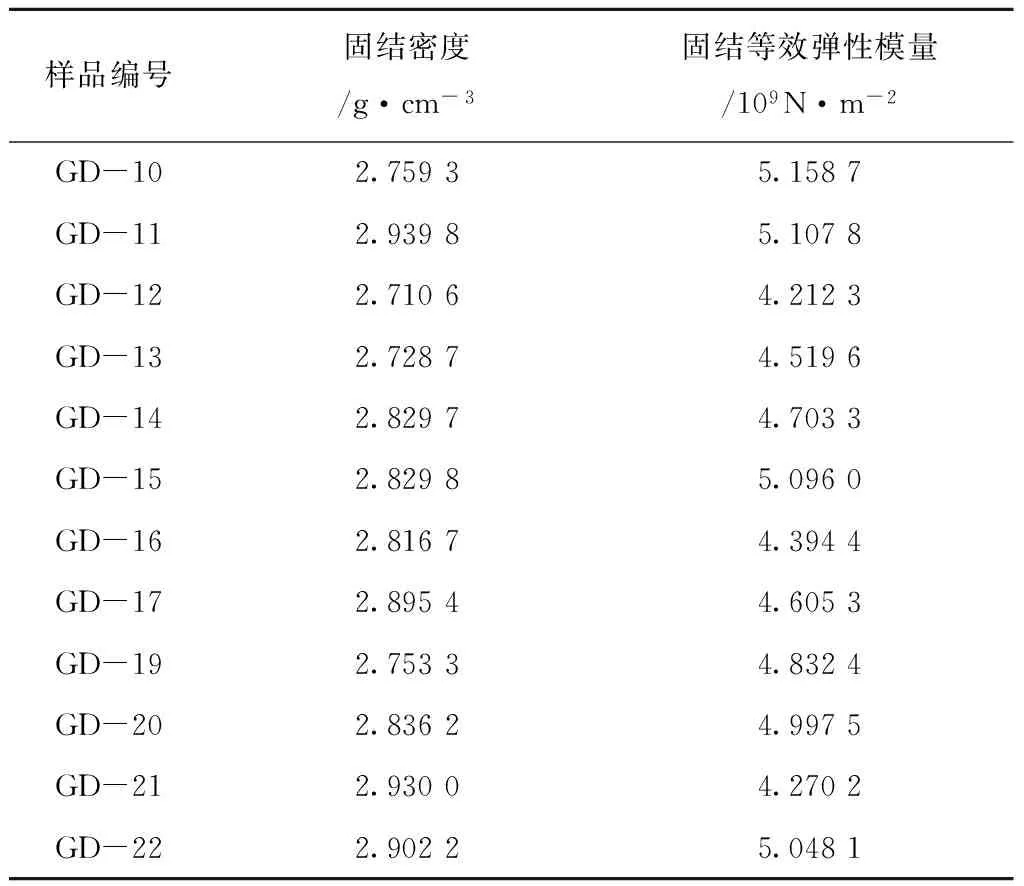
表6　沉积物固结密度和等效固结弹性模量

等效固结模量Ms考虑的是沉积物固结后不含水无空隙的极限状态。由式(9)可以换算出饱和沉积物的等效模量Mn。

(9)

式中，Mn为饱和沉积物的等效弹性模量，Mw为孔隙水的等效弹性模量，Ms为固结模量。

孔隙水的等效弹性模量[5]取Mw=2.374 0×109N/m2，算得饱和沉积物的等效弹性模量如表7。

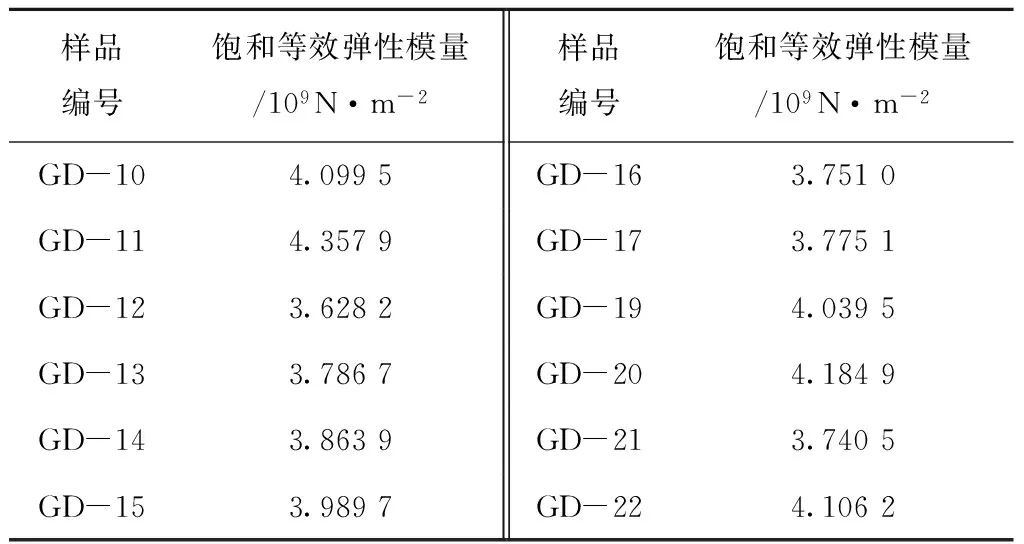
表7　沉积物饱和等效弹性模量

本文计算得出的沉积物的等效模量值趋近于Hamilton和Bachman[5]的大陆台阶(大陆架和大陆坡)环境的模量值，在3.14×109～4.51×109N/m2之间。

4.2沉积物双复合参数-声速经验公式的建立与分析

利用表7的数据、等效固结弹性模量Ms和等效固结体积模量Ks的换算关系，可得沉积物样品的等效体积模量Ks如表8。

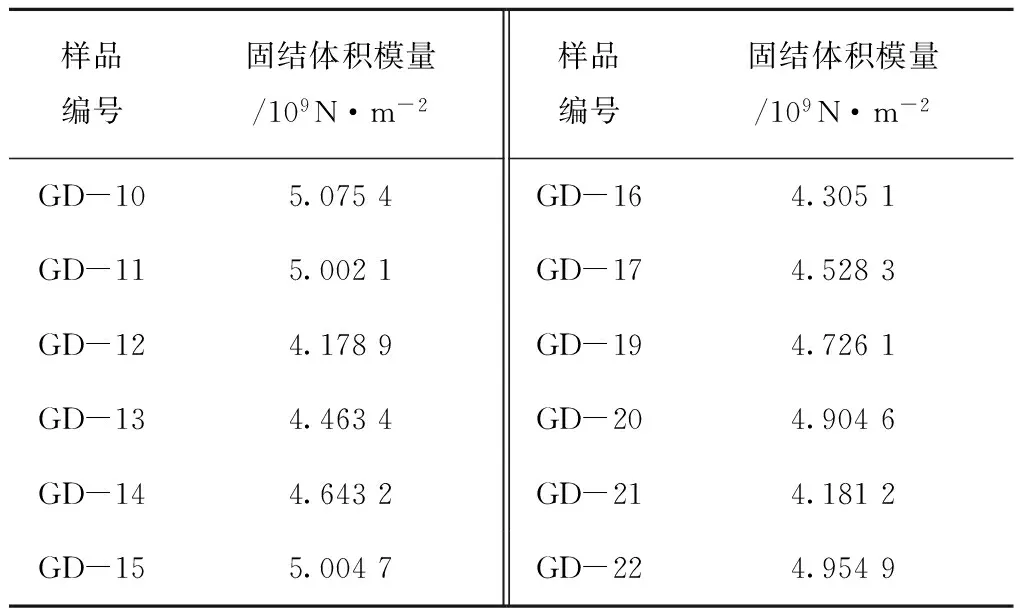
表8　沉积物固结体积模量

由理论关系Kn=nKw+(1-n)Ks，可求得饱和沉积物的体积模量Kn如表9。

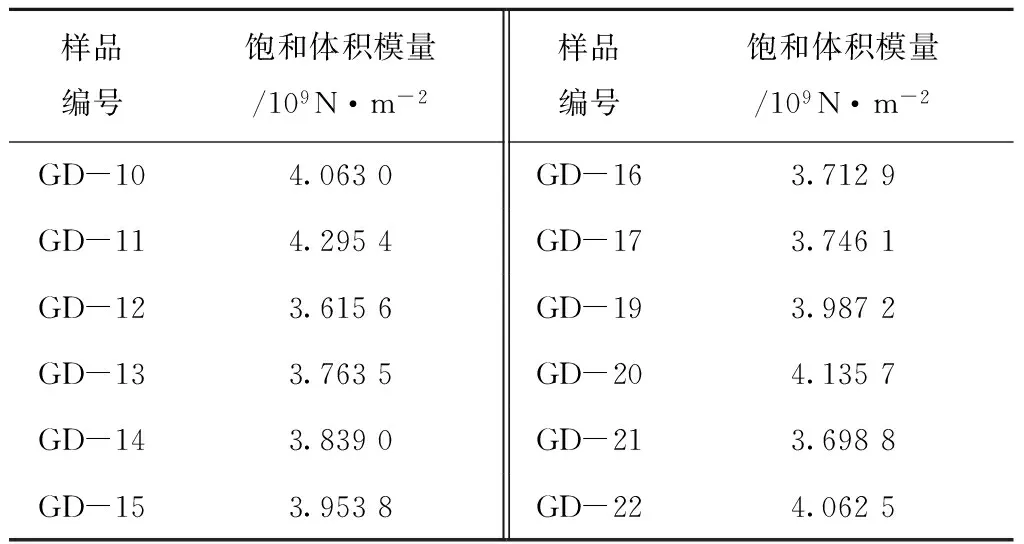
表9　饱和沉积物体积模量

文献[9]得到了海底沉积物声速多项式模型，本文取其前4项得到：

CP=CPr(1+a1x+a2x2+a3x3)×

(1+b1y+b2y2+b3y3)，

(10)

式中，CPr=(Ms/ρs)1/2，x=n(1-Kw/Ks)，y=n(1-ρw/ρs)，a1、a2、a3和b1、b2、b3为待定多项式系数。

利用表6～表9数据，可以确定多项式(10)的待定系数，得到双复合参数-声速经验公式为：

CP=2 860.9(1-0.667 8x+3.956 5x2-3.197 0x3)

×(1+1.513 7y+1.711 1y2-0.696 6y3).

(11)

根据实验数据，复合参数x=n(1-Kw/Ks)的取值范围为0.147 9～0.419 1，复合参数y=n(1-ρw/ρs)的取值范围为0.190 0～0.538 4，式(11)所刻画的声速曲面见图6。图中从蓝色到黄色代表沉积物的声速的增大过程。

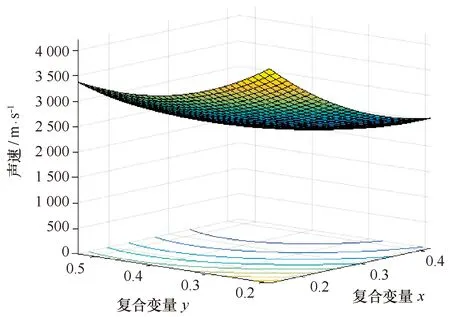
图6　沉积物声速曲面Fig.6　Surface of velocity of sediments

利用表1数据，可以建立孔隙度-声速回归公式为:

CP=4 093.85-129.93n+2.231 2n2-0.013 29n3.

(12)

图6中，沉积物声速随着复合参数x和复合参数y的增大而变小，并且在(x，y)≈(0.147 9，0.19)处声速取得最大值。这和式(12)的沉积物声速随着孔隙度的增大而减小的结论是一致的。

4.3预报声速与测量声速误差比较

把复合参数x=n(1-Kw/Ks)，y=n(1-ρw/ρs)数值代入曲面方程式(11)，及把孔隙度数值代入式(12)，可以分别计算出两个公式的声速预报值。与沉积物样品测量声速值比较，对应的误差如表10和表11。

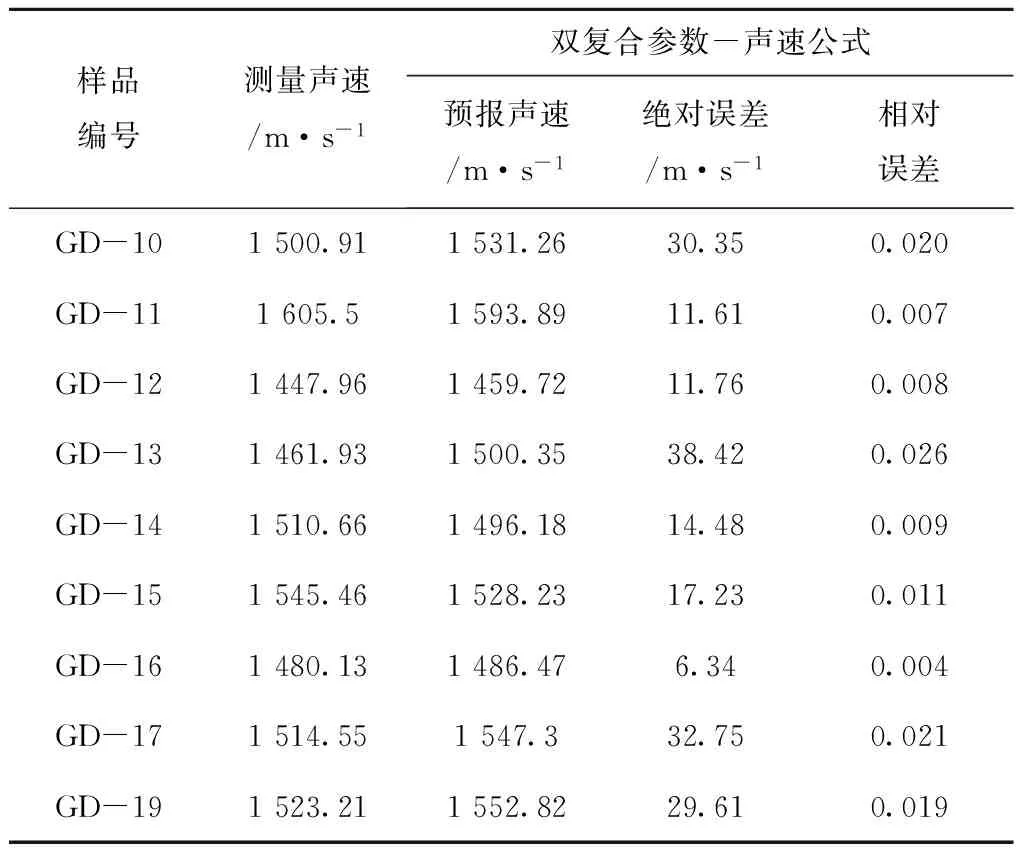
表10　双复合参数-声速公式计算沉积物声速预报值与误差

通过对比可知，式(11)的双复合参数-声速公式

的绝对误差和相对误差最大值分别为：38.42 m/s、0.026；式(12)的孔隙度-声速公式的绝对误差和相对误差最大值分别为：151.32 m/s、0.094 45。可见前者声速预报误差约是后者的1/4。

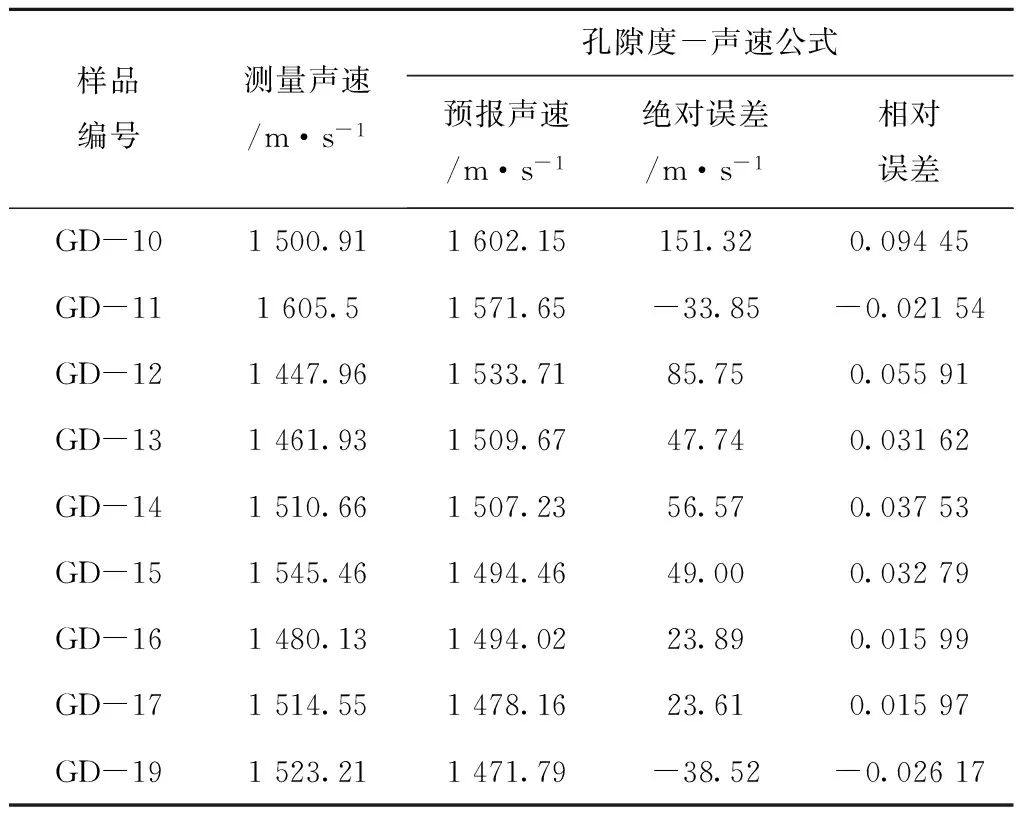
表11　孔隙度-声速公式计算沉积物声速预报值与误差

5　结论

围压相同时轴向应变增大静弹性模量也增大；沉积物动弹性模量与孔隙度的相关性很高，相关系数达0.97，动弹性模量是静弹性模量的10～100倍。在应变加载到结束过程声速不断变化；本次试验样品的平均声速随着平均静弹性模量的增加，由大变小又由小变大，存在声速最小值。分别建立了双复合参数-声速和孔隙度-声速经验公式，分析结果表明双复合参数-声速经验公式预报声速的误差远小于孔隙度-声速经验公式预报声速的误差。

[1]Stoll R D. Measuring parameters that control propagation in granular sediments near the sea floor[C]//Proceedings of the 135th Meeting of the Acoustical. Seattle: Society of America, 1998: 1611-1612.

[2]Stoll R D, Sun Yuefeng, Bitte I. Seafloor properties from penetrometer tests[J]. IEEE Journal of Oceanic Engineering, 2007, 32(1): 57-63.

[3]Lu Bo, Li Ganxian, Huang Shaojian, et al. The three results of sound velocity variance in sediments during controlled stress-strain testing from the South China Sea[J]. Marine Georesources and Geotechnology, 2002, 20(3): 177-186.

[4]Chen Minpen, Shieh Y T, Chyan J M. Acoustic and physical properties of surface sediments in northern Taiwan strait[J]. Acta Oceanographica Taiwanica, 1988(21): 92-118.

[5]Hamilton E L, Bachman R T. Sound velocity and related properties of marine sediments[J]. Journal of Acoustical Society of America, 1982, 72(6): 1891-1904.

[6]Hamilton E L. Geoacoustic modeling of the sea floor[J]. Journal of Acoustical Society of America, 1980, 68(5): 1313-1340.

[7]Anderson R S. Statistical correlation of physical properties and sound velocity in sediments[M]//Hampton L. Physics of Sound in Marine Sediments. US: Springer, 1974: 48l-5l8.

[8]卢博, 李赶先, 孙东怀, 等. 中国东南近海海底沉积物声学物理性质及其相关关系[J]. 热带海洋学报, 2006, 25(2): 12-17.

Lu Bo, Li Ganxian, Sun Donghuai, et al. Acoustic-physical properties of seafloor sediments from nearshore southeast China and their correlations[J]. Journal of Tropical Oceanography, 2006, 25(2): 12-17.

[9]龙建军, 李赶先. 海底沉积物声速与物理性质的理论关系[J]. 声学学报, 2015, 40(3): 462-468.

Long Jianjun, Li Ganxian. Theoretical relations between sound velocity and physical-mechanical properties for seafloor sediments[J]. Acta Acustica, 2015, 40(3): 462-468.

[10]龙建军, 李赶先, 邹大鹏. 海底沉积物纵波波速与物理-力学性质的理论关系和比较[J]. 海洋学报, 2014, 36(7): 111-117.

Long Jianjun, Li Ganxian, Zou Dapeng. Theoretical relations of longitudinal wave velocity and physical-mechanical properties for seafloor sediments and comparison[J]. Haiyang Xuebao, 2014, 36(7): 111-117.

[11]朱思哲, 刘虔, 包承纲, 等. 三轴试验原理与应用技术[M]. 北京: 中国电力出版社, 2003.

Zhu Sizhe, Liu Wen, Bao Chenggang, et al. Three Axis Test Principle and Application Technology[M]. Beijing: China Power Press, 2003.

[12]国家质量技术监督局, 中华人民共和国建设部. GB/T 50123-1999, 土工试验方法标准[S]. 北京: 中国计划出版社, 2007.

The State Bureau of Quality and Technical Supervision,Ministry of Construction of the People's Republic of China. Soil Test Method Standard (GB/T50123-1999)[S]. Beijing: China Planning Publishing House,2007.

[13]刘寄能, 梁元博, 卢博, 等. 南海两海区海底沉积物的声速和应力-应变特征[J]. 南海海洋科学刊, 1989(9): 87-94.

Liu Jineng, Liang Yuanbo, Lu Bo, et al. Acoustic velocity and stress-strain characteristics of seabed sediments in two areas of South China Sea[J]. The Volume of South China Sea Marine Science, 1989(9): 87-94.

[14]Hamilton E L. Elastic properties of marine sediments[J]. Journal of Geophysical Research, 1971, 76(2): 579-604.

[15]Hamilton E L. Vp/Vs and Poisson's ratios in marine sediments and rocks[J]. Journal of Acoustical Society of America, 1979, 66(4): 1093-1101.

[16]Mavko G, Mukerji T, Dvorkin J. The rock physics handbook: tools for seismic analysis in porous media[M]. London: Cambridge University Press, 2003.

索安宁，王鹏，袁道伟，等. 基于高空间分辨率卫星遥感影像的围填海存量资源监测与评估研究——以营口市南部海岸为例[J]. 海洋学报， 2016， 38(9):54-63，doi:10.3969/j.issn.0253-4193.2016.09.006

Suo Anning, Wang Peng, Yuan Daowei, et al. Study on monitoring and analysis of existing sea reclamation resource based on high resolution satellite remote sensing imagery: A case in south coast of Yingkou[J]. Haiyang Xuebao， 2016， 38(9):54-63， doi：10.3969/j.issn.0253-4193.2016.09.006

Relationship between sound velocity and physical mechanical properties of seafloor sediments in controlled three axis stress-strain

Long Jianjun1， Zhou Huajian1， Li Ganxian2， Chen Cong1

(1.SchoolofElectromechanicalEngineering，GuangdongUniversityofTechnology，Guangzhou510006，China;2.KeyLaboratoryofMarginalSeaGeology，SouthChinaSeaInstituteofOceanology，ChineseAcademyofSciences，Guangzhou510301，China)

The sediment cores， from shallow seafloor in depth of 100-400 meters (about 2 m depth buried) in an area of the South China Sea， have been performed a simultaneous triaxial strain-acoustic measurement near seabed water pressure. The results show that the sediment longitudinal wave velocity has two characteristics: (1) the longitudinal wave velocity in sediments keeps changing in the process of strain applied from start to end; (2) the average of the speed of sound changes from large to small and then from small to large with the average of the static elastic modulus increasing， and there is a minimum during the course of the average of the speed of sound change. These results are related to physical and mechanical properties and confining pressure of the shallow seafloor sediments， and the changes of the state in which particles of these sediments combine together. In addition， sediment dynamic elastic modulus and porosity has a good negative correlation， and that results from increases of the water content with increases of porosity. Dynamic elastic modulus is 10 to 100 times the static elastic modulus， since the large difference between the strain magnitude resulted from triaxial strain-test and the one generated by wave vibrations is primarily related to that. Two empirical formulas of dual complex parameters-velocity and porosity-velocity were established with the experimentally measured data in this paper. The analysis of results shows that the error in sound speed predicted by the formula of composite double parameters-velocity is approximately a quarter of that predicted by the formula of the porosity-velocity， and it shows that the formula of composite double parameters-velocity is more effective．

South China Sea; seafloor sediment; sound velocity; three axis stress-strain; empirical formula

2015-12-10；

2016-03-26。

国家自然科学基金(41176034, 41476028)。

龙建军(1960—)，男，广西壮族自治区玉林市人，博士，副教授，主要从事海洋沉积声学、海洋声学测量技术研究。E-mail:longjj@gdut.edu.cn

P733.23

A

0253-4193(2016)09-0046-08