一个典型南海北部第二模态内孤立波的观测分析

钱洪宝，黄晓冬，田纪伟

(1. 中国海洋大学 物理海洋教育部重点实验室，山东 青岛 266100; 2. 中国21世纪议程管理中心， 北京 100038)



一个典型南海北部第二模态内孤立波的观测分析

钱洪宝1，2，黄晓冬1*，田纪伟1

(1. 中国海洋大学 物理海洋教育部重点实验室，山东 青岛 266100; 2. 中国21世纪议程管理中心， 北京 100038)

第二模态内孤立波在海洋中极少被观测到。本文基于潜标高时空分辨率观测数据，对南海北部陆架区的一个典型第二模态内孤立波进行了分析。结果表明，该第二模态内孤立波的流核出现在135 m深度处，其最大水平流速为0.66 m/s，传播方向为西偏北58°。沿传播方向的内孤立波流速分布在80～170 m的深度范围内，而与传播方向相反的逆流出现在海表和海底附近。垂向模态分析表明，该第二模态内孤立波水平流速的垂向结构与理论结果吻合良好。能量计算结果显示其动能密度的垂向积分可达14 kJ/m2，而波峰线方向单位长度上的动能估算值为5.98 MJ/m。尽管该第二模态内孤立波的动能比陆架区第一模态内孤立波小1个量级，但其高达0.045 s-1的流速垂向剪切约为典型第一模态内孤立波的2倍，表明其导致的混合可能更强。

内孤立波；第二模态；潜标；观测；南海

1　引言

海洋内孤立波(internal solitary wave，ISW)是一种特殊的、具有强非线性特征的海洋内波，也被称为非线性内波。由于极窄的波宽，内孤立波的非静力频散效应不可忽略，其与非线性变陡效应间的平衡能够令内孤立波在传播过程中保持波型不变。内孤立波引起的极强突发流和等密度面断崖式下沉对海洋工程作业和潜艇水下航行的安全具有严重危害，对海洋声传播过程、生态环境和鱼类活动有重要影响，其流速剪切所诱发的极强混合对海洋垂向热结构有重要的调制作用。

根据振幅垂向结构所拥有的极值点个数，海洋内波可以分为不同的垂向模态。按照定义，第一模态内波所造成的等密度面起伏在整个深度上同位相。在海表面，第一模态内孤立波引起的起伏非常微弱，但在海表面附近出现的流核，使其能够在现场观测中较为容易地被捕捉到。在下层海洋，第一模态内孤立波的水平流与上层反向。另一方面，第一模态内孤立波能够在海表面产生强辐聚/辐散，所引起的海表面粗糙度变化使其可以通过卫星遥感手段进行观测。在现场和卫星遥感等多种观测手段的共同支持下，第一模态内孤立波被证实在世界海洋中存在着较为广泛的分布。

与第一模态内孤立波不同，第二模态内孤立波引起的等密面起伏在温跃层上下反位相变化。由于第二模态内孤立波的流核出现在海表面以下，导致通过现场和卫星遥感等手段对其进行观测存在困难，使其极少在实际海洋中被观测到。Konyaev等[1]报道了发生在印度洋西部马斯克林(Mascarene)海脊上的一个高模态内孤立波，发现该内孤立波经过时等温线起伏在150 m上下分别呈现出上凸和下凹的形态，这可能是有关海洋第二模态内孤立波的首个报道。Shroyer等[2]报道了在美国新泽西州沿岸观测到的一个第二模态内孤立波波列。在南海北部陆架区，Yang等[3]利用潜标观测到该海域存在着第二模态内孤立波，并在后续观测中发现其大多在冬季发生[4]。Ramp等[5]在台湾岛以南的恒春海山北部观测到一个第二模态内孤立波，并认为其生成机制与局地潮地相互作用产生的背风波有关。一般来说，相对第一模态内孤立波，第二模态内孤立波的流速较弱和振幅较小，但由于其流核位于海面以下，对海上工程的水下作业安全的影响可能会更严重。

南海北部是全球内孤立波最强和最为活跃的海域，因此是近10年来海洋波动研究的热点[6—8]。极强的内孤立波在吕宋海峡生成后，向西传播穿过深海盆，传入陆坡陆架区。受到层结[9—10]和地形[11]变化的影响，南海北部海域尤其是陆坡陆架区内波[12]的形态多变。然而，由于第二模态内孤立波的观测极为困难，还不能完全掌握该海域第二模态内孤立波的特征，对其所携带的能量大小尚缺乏认知。本文基于潜标高时空分辨率观测数据，对南海北部陆架区的一个典型第二模态内孤立波的特征和模态结构进行了研究，并对其能量和所引起的流速剪切进行了分析。本文主要分为5个部分，第二部分为数据介绍，第三部分给出了第二模态内孤立波的观测结果，第四部分给出了理论分析、能量计算和流速剪切分析结果，最后为讨论和结论。

2　数据介绍

本文使用的数据来自于中国海洋大学“南海潜标观测网”IW7潜标的观测结果。IW7潜标位于南海北部陆坡陆架区东沙岛以北海域，水深约为252 m(图1)。该潜标在位时间为2013年10月下旬至2014年6月上旬。潜标在218 m深度上安装了一台观测姿态向上的150 kHz声学多普勒流速剖面仪(Acoustic Doppler Current Profiler，ADCP)。该ADCP的采样时间间隔为2 min，观测层数为60层，观测范围为表层至深约210 m，层厚为4 m。潮流、中尺度涡和内孤立波等过程会影响潜标姿态，进而改变ADCP自身和观测深度。为方便分析，将所观测的流速数据插值到间隔5 m的标准层上。在分析前，首先计算了正压流速的时间序列，随后在水平流速观测结果中减去该正压流部分得到斜压流。

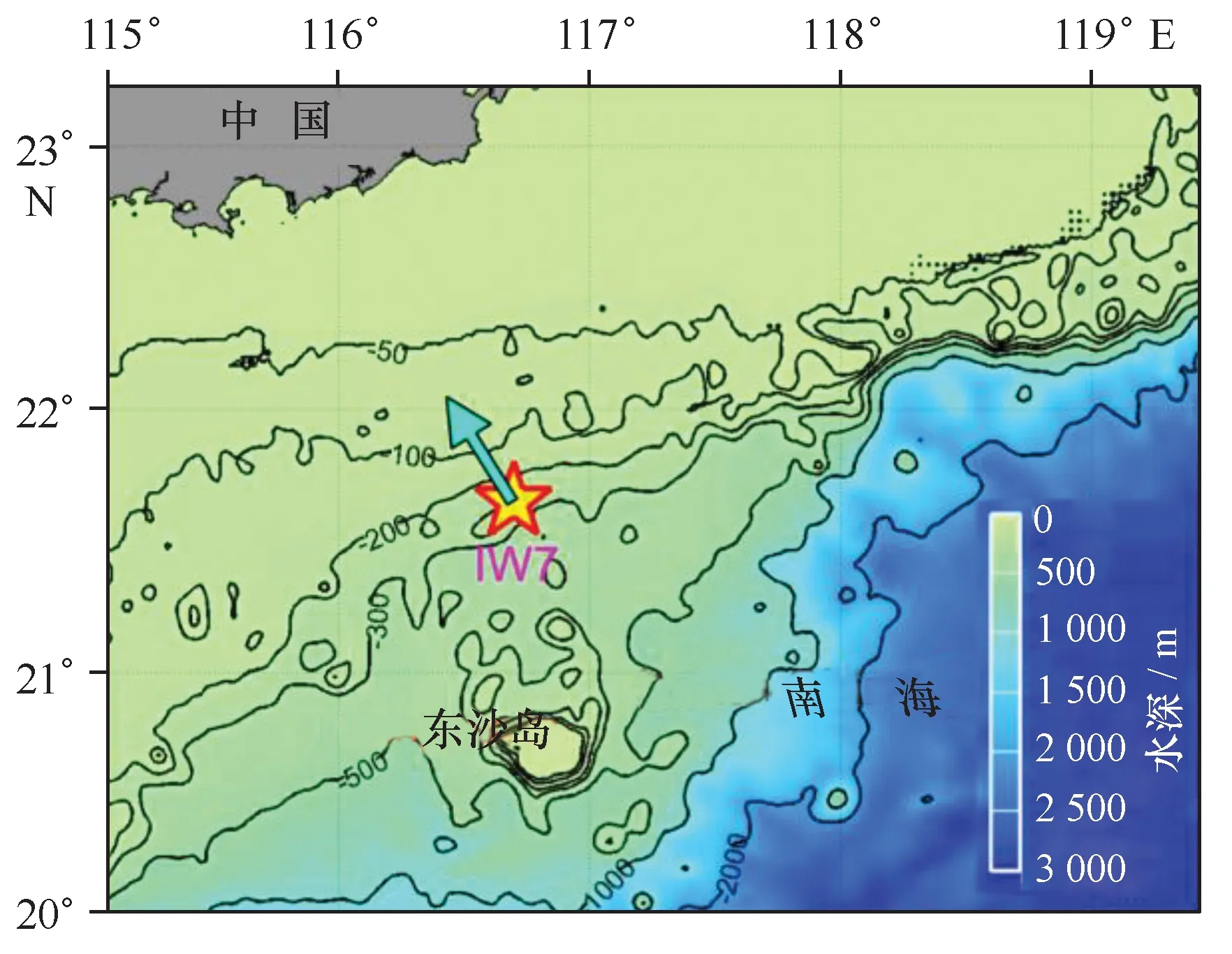
图1　南海北部地形图及IW7潜标的位置Fig.1　Bathymetry of the northern South China Sea and location of mooring IW7箭头为所观测第二模态内孤立波的传播方向The cyan arrow denote the propagation direction of mode-2 ISW

3　观测结果

图 2给出了IW7潜标在2013年10月30日的ADCP东西和南北方向流速观测结果。从图中可以看到在当日上午9时前后数个内孤立波连续经过IW7潜标。第一模态内孤立波发生时的水平流速在表层附近最强。然而，上午9时前后所出现的内孤立波，其最大水平流速出现在100 m以深，并且水平流速剖面呈现出三明治结构，中层流速方向与上下两层反向。上述特征表明该内孤立波与平常观测到的第一模态内孤立波显著不同。

计算内孤立波到达前30～40 min的时间平均流速剖面作为背景流，并在观测结果中减去此背景流以获得内孤立波自身的流速。随后，根据内孤立波流核处的东西和南北方向流速，计算得到内孤立波的传播方向为西偏北58°。此处，通过以下方法将东西和南北方向流速转换到平行和垂直于内孤立波传播方向的两个分量[13]：

(1)

式中，θ为内孤立波传播方向，uf为平行内孤立波传播方向的分量，ua为垂直于内孤立波传播方向的分量。uf的计算结果如图3a所示。该第二模态内孤立波由至少5个孤立子组成，前两个孤立子的持续时间分别为22 min和14 min。沿传播方向的第二模态内孤立波流速uf分布在80～170 m的深度范围内，而与传播方向相反的逆流出现在海表和海底附近。首个孤立子的水平流速最强，最大达0.66 m/s，出现在135 m深度处。后续孤立子所诱发的水平流速依次减小，显示波包中的孤立子按照由强到弱的顺序排列。在海表和底部出现了与内孤立波传播方向相反的逆流，但其流速相对较弱。

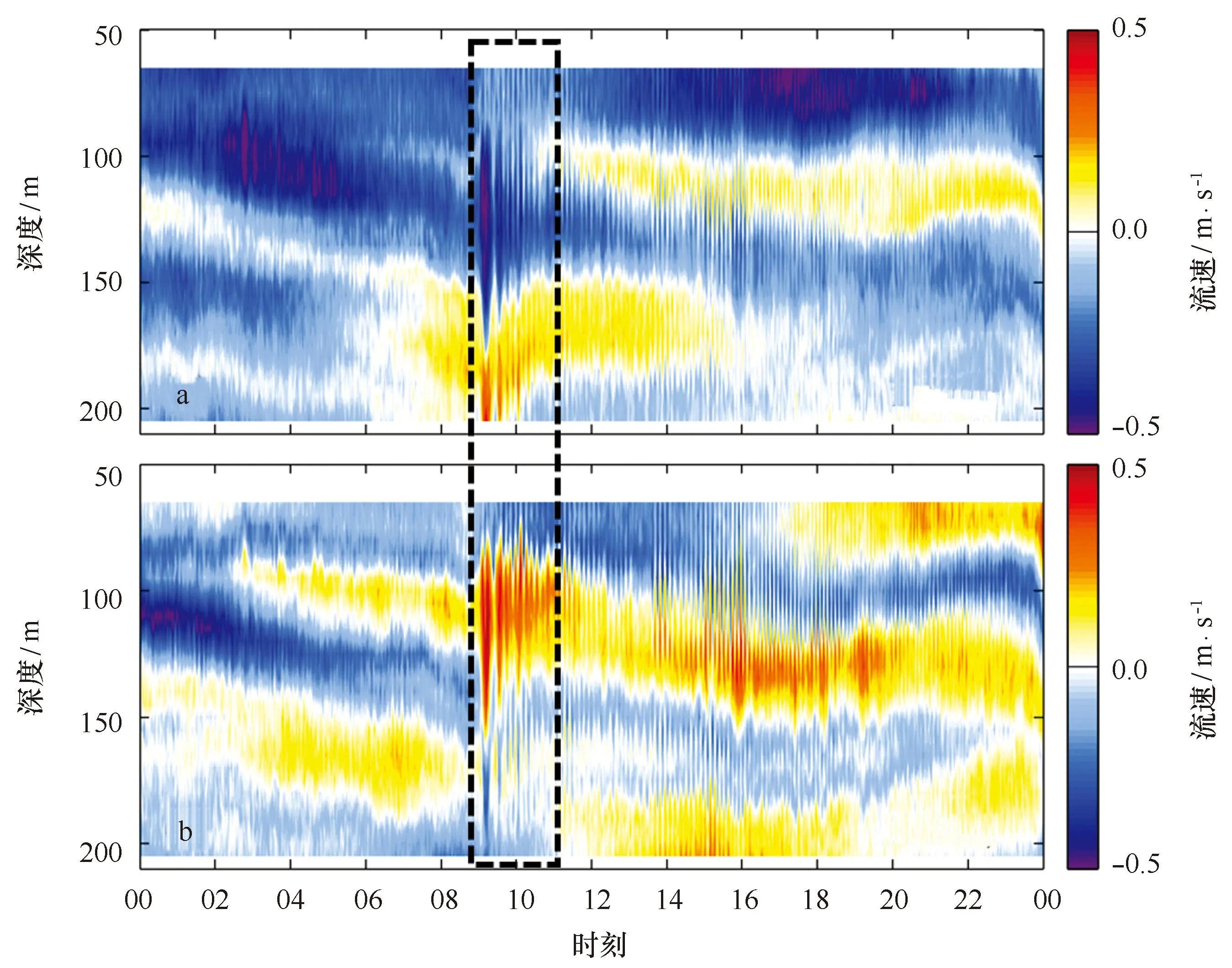
图2　2013年10月30日IW7潜标的东西(a)和南北(b)方向流速观测结果Fig.2　The full-day zonal (a) and meridional (b) velocity measurements of mooring IW7 on 30 October 2013

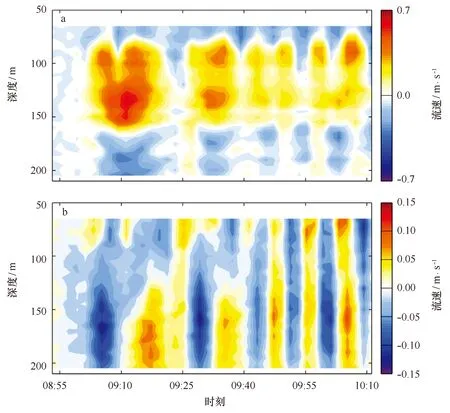
图3　2013年10月30日上午于IW7处观测到的第二模态内孤立波，a为沿内孤立波传播方向流速分量，b为垂向流速分量Fig.3　The mode-2 ISWs recorded on 30 October 2013 at mooring IW7. a.The current velocity along thepropagation direction of ISWs， b.vertical velocity

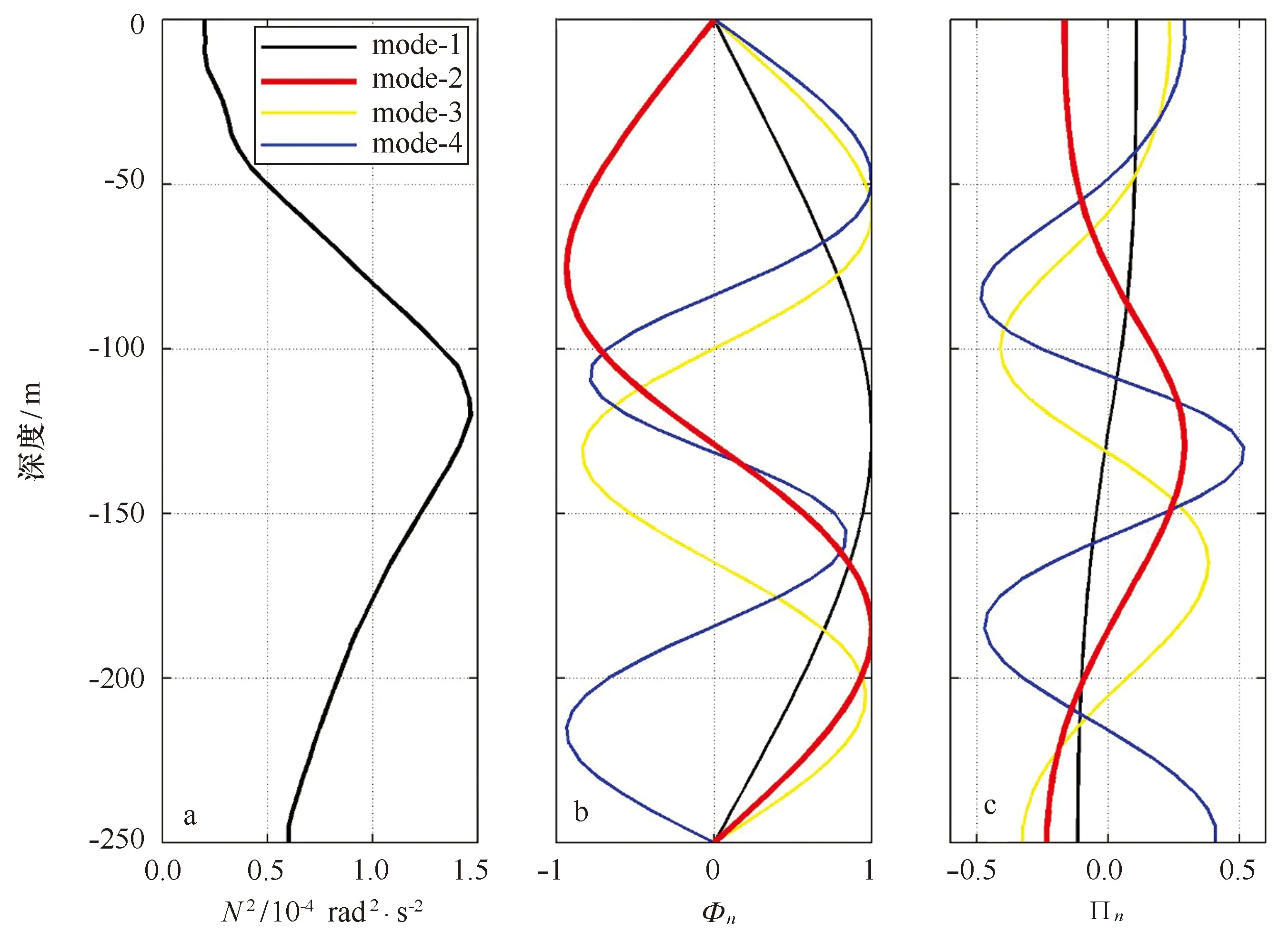
图4　IW7潜标处浮性频率剖面图(a)和前4个模态内波的振幅(b)和水平流速(c)的垂向结构函数图Fig.4　The N2 at mooring IW7 extracted from WOA01 data (a)， the vertical displacement of first four baroclinic modes(b) and the horizontal velocity of first four baroclinic modes(c)

图3b给出了第二模态内孤立波经过时的垂向流速观测结果。在首个孤立子经过时，以90 m为界限，上下两层水体在垂向上反位相移动。在首个孤立子前缘，下层水体向下移动，最大流速达0.13 m/s，而上层流体向上移动，其速度相对较小；在孤立子后缘，下层水体向上运动，最大流速达0.10 m/s，而上层水体向下运动。这是与第一模态内孤立波的显著差异之一。第二个孤立子所引起垂向流速的结构具有相似的特征。第三及后续的孤立子经过时垂向流速在上层和下层反位相的特征并不明显。这可能是因为这些孤立子自身强度较弱，导致难以持续保持第二模态内波垂向流速上下反位相的特性。

4　分析结果

4.1模态分析

海水层结是决定各个模态内波垂向结构的主要因素。此处，在WOA01冬季气候态数据中提取了IW7处的温度和盐度剖面，并计算得到IW7处的层结。如图4a所示，冬季IW7处的温跃层位于120 m附近，处于水体的中部。N2最高为1.467 rad2/s2，显著弱于其他季节。根据层结信息，利用Sturm-Liouville方程：

(2)

及在海面和海底的边界条件Φn(0)=Φn(-H)=0 ，计算得到了各个模态内波振幅的垂向结构Φn(z)和各个模态线性内波的传播速度cn。图4b给出了Φn(z)的垂向结构，可以看到随着模态数的增加，内波振幅的拐点增多。其中，第一模态内波振幅的极大值位于水深125 m处，而第二模态内波振幅的极大值位于75 m和185 m处。

通过式(3)，计算各个模态内波水平流速的垂向结构：

(3)

计算结果如图4c所示。第一模态内波水平流的流向拐点出现在125 m深处。第二模态内波的理论流速最大值出现在130 m深处，而流向的拐点出现在75 m和185 m深处。在IW7处所观测到的第二模态内孤立波，其沿传播方向的流速最大值出现在135 m深度处，与理论值极为接近。另一方面，观测中第二模态内孤立波水平流所具有的三明治结构与理论结果一致，并且流速拐点所在的深度与理论较为吻合。

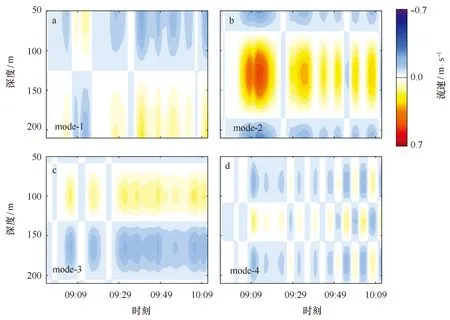
图5　对第二模态内孤立波沿传播方向流速进行垂向模态分解后的结果，a-d为前4个垂向模Fig.5　The horizontal velocity of first four baroclinic modes during the passage of mode-2 ISW

为进一步分析该内孤立波的模态结构，此处使用以下公式：

(4)

采用最小二乘方法将内孤立波流速剖面分解到各个垂向模态上，结果如图5所示。可以看到，观测中内孤立波在135 m附近的流核主要体现第二模态内波的特征，而模态分析结果表明，第二模态流速最大值达0.55 m/s。模态分解得到的其他模态分量与所观测得到的内孤立波形态完全不同，并且最大流速均小于0.2 m/s。这些分析结果进一步表明该内孤立波为第二模态内孤立波。

4.2动能分析

此处，使用下式计算内孤立波动能密度在垂向的积分：

(5)

式中，ρ(z)为在WOA01冬季气候态数据中提取得到的IW7处密度剖面，计算结果如图6所示。可以看到，首个孤立子动能密度的垂向积分峰值可达14 kJ/m2。平均来看，第二模态内孤立波能量占所有模态内孤立波能量的比例约为60%。

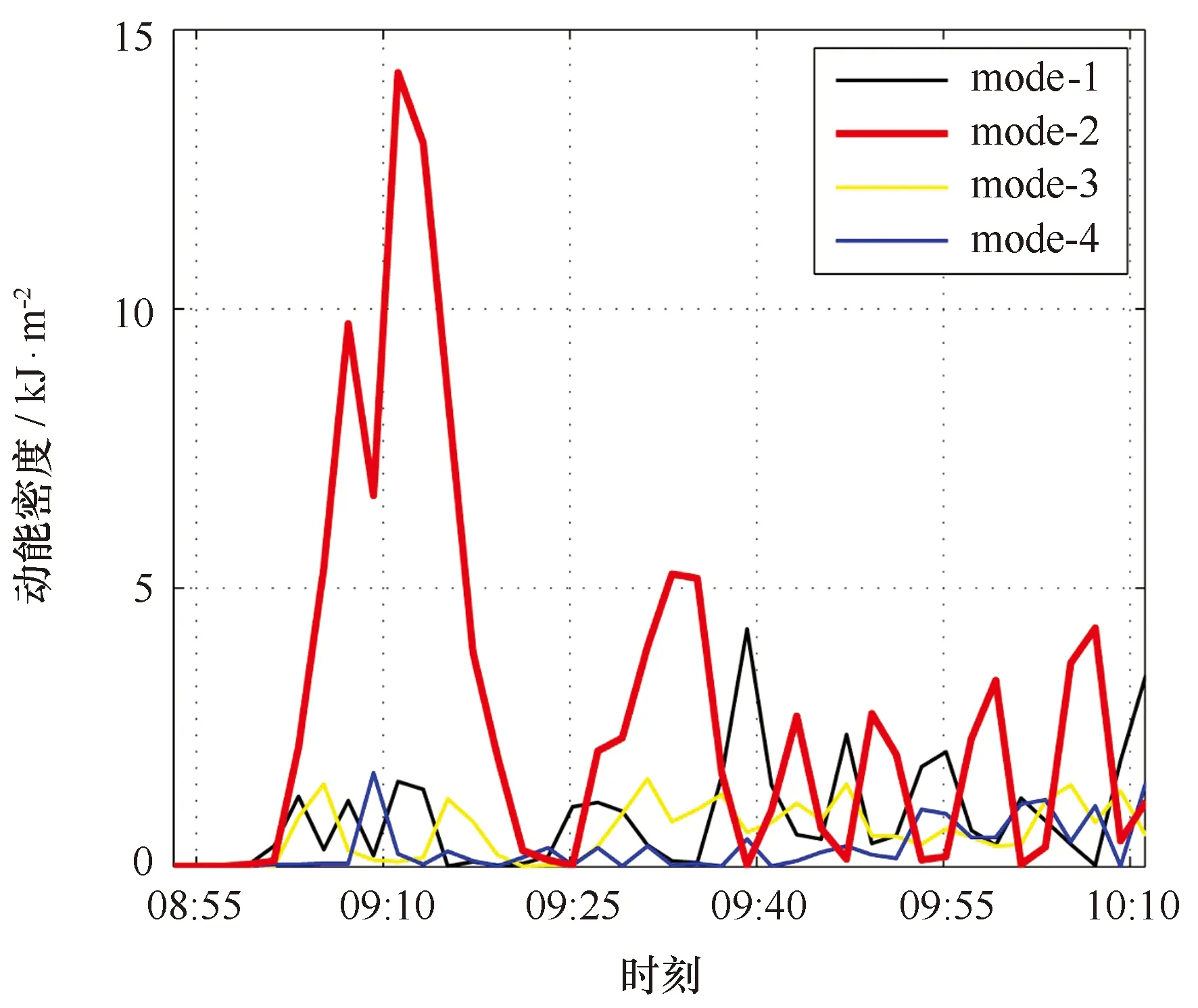
图6　前4个模态动能密度的垂向积分结果 Fig.6　The depth-integrated kinetic energetic density for the first four modes

KdV方程通常用于分析内孤立波特征参数及传播演变过程：

(6)

式中，η为内孤立波振幅，α和γ分别为非线性系数和频散系数。本文根据式(7)，

(7)

计算得到第二模态内孤立波所对应的非线性系数为0.004 5 s-1。通过公式(2)计算得到的第二模态内波的线性传播速度c2为0.37 m/s。根据垂向流速观测结果，对其在时间上进行积分估算得到首个孤立子在垂向上的最大振幅η约为44 m。因此，通过内孤立波传播速度的计算公式：

(8)

估算该第二模态内孤立波的传播速度为0.436 m/s。使用公式，将水平流速的时间序列转化到空间坐标系，进而得到波峰线方向单位长度上第二模态内孤立波的动能为5.98 MJ/m2。Alford等[14]在水深331 m处观测的第一模态内孤立波动能大约在10～100 MJ/m2范围内。我们所观测的第二模态内孤立波动能比其小一个量级。

4.3流速剪切

根据所观测到的第二模态内孤立波水平流速，本文进一步计算了其所导致的流速剪切，如图7所示，内孤立波经过时在水深80 m和160 m深处诱发的流速剪切极强，其量值分别达0.035 s-1和0.045 s-1。Klymak等[15]在南海北部深水区观测到一个振幅达170 m、水平流速超过2 m/s的极强第一模态内孤立波，计算结果显示其所引发的流速剪切不大于0.02 s-1。二者比较可以发现，我们所观测到的第二模态内孤立波所引发的流速剪切约为其2倍。垂向剪切较强意味着能量耗散较快。尽管第二模态内孤立波的动能比第一模态内孤立波小1个量级(如上一小节所述)，但其能量耗散极有可能比第一模态内孤立波更强，因此其难以如第一模态内孤立波一样在生成后仍传播较远的距离。Qian等[12]基于数值模拟试验也获得了同样的结论。

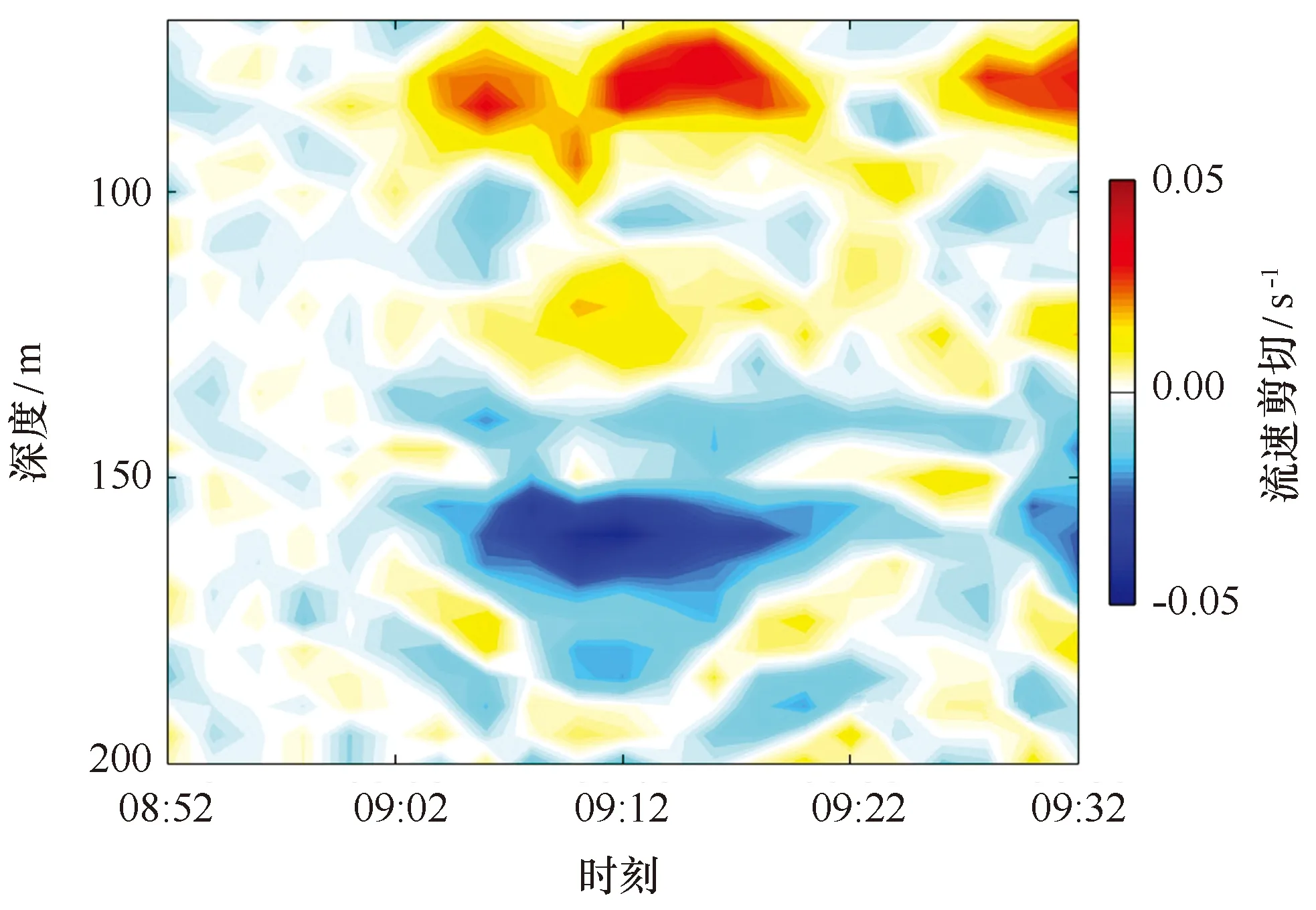
图7　第二模态内孤立波波列中首个孤立子的水平流速剪切Fig.7　The vertical shear of horizontal velocity during the passage of first soliton

5　讨论和结论

在前人的理论和试验研究中，共提出了4种第二模态内孤立波的生成机制。分别为第一模态内孤立波与变化地形相互作用[11—12,16—17]、第一模态内孤立波的反射[18]、当温跃层位于水体中部时流体经过下凹地形[19]和重力流侵入三层流体[20]等。从图2中可以看到，在第二模态内孤立波出现前后并没有大振幅第一模态内孤立波出现，因此其生成应与第一模态内孤立波无关。图4a显示IW7处冬季温跃层位于水体的中部，这可能是产生该第二模态内孤立波的原因。

本文基于潜标高时空分辨率ADCP流速观测数据，对在南海北部陆架区出现的一个第二模态内孤立波的特征进行了分析。研究结果表明，第二模态内孤立波的流核出现在135 m深度处，其最大水平流速为0.66 m/s，传播方向为西偏北58°。沿传播方向的内孤立波流速分布在80～170 m的深度范围内，而与传播方向相反的逆流出现在海表和海底附近。使用WOA01气候态温度和盐度数据对第二模态内孤立波水平流速进行了垂向模态分析，结果显示其最大流速深度、流向拐点深度等与理论结果吻合良好。首个孤立子动能密度的垂向积分峰值可达14 kJ/m2，而波峰线方向单位长度上的动能估算值为5.98 MJ/m。尽管该第二模态内孤立波的动能比第一模态内孤立波小1个量级，但其高达0.045 s-1的流速垂向剪切约为典型第一模态内孤立波的2倍，因此其能量耗散可能更强，意味着其难以如第一模态内孤立波一样在生成后仍传播较远的距离。

[1]Konyaev K V, Sabinin K D, Serebryany A N. Large-amplitude internal waves at the Mascarene Ridge in the Indian Ocean[J]. Deep-Sea Res Ⅰ, 1995, 42(11/12): 2075-2091．

[2]Shroyer E L, Moum J N, Nash J D. Mode 2 waves on the continental shelf: Ephemeral components of the nonlinear internal wavefield[J]. Journal of Geophysical Research, 2010, 115(C7): 1-12．

[3]Yang Y J, Tang T Y, Chang M H, et al. Solitons Northeast of Tung-Sha Island during the ASIAEX Pilot Studies[J]. Journal of Oceanic Engineering, 2004, 29(4): 1182-1199．

[4]Yang Y J, Fang Y C, Chang M-H et al. Observations of second baroclinic mode internal solitary waves on the continental slope of the northern South China Sea[J]. Journal of Geophysical Research, 2009, 114(C10): 1-15．

[5]Ramp S R, Yang Y J, Reeder D B, et al. Observations of a mode-2 nonlinear internal wave on the northern Heng-Chun Ridge south of Taiwan[J]. Journal of Geophysical Research, 2012, 117(C3): 1-11．

[6]Cai S, Xie J, He J. An overview of internal solitary waves in the South China Sea[J]. Surveys in Geophysics, 2012, 33(5): 927-943．

[7]Alford M H, Peacock T, MacKinnon J A, et al. The formation and fate of internal waves in the South China Sea[J]. Nature, 2015, 521(7550): 65-69．

[8]蔡树群, 何建玲, 谢皆烁. 近10年来南海孤立内波的研究进展[J]. 地球科学进展, 2011, 26(7): 703-710．

Cai Shuqun, He Jianling, Xie Jieshuo. Recent decadal progress of the study on internal solitons in the South China Sea[J]. Adcances in Earth Science,2011, 26(7): 703-710．

[9]Chen Zhi-wu, Xie Jieshuo, Wang Dongxiao, et al. Density stratification influences on generation of different modes internal solitary waves[J]. Journal of Geophysical Research, 2014, 119(10): 7029-7046．

[10]Xie J, Pan J, Jay D A. Multimodal internal waves generated over a Subcritical Ridge: impact of the upper-ocean stratification[J]. Journal of Geophysical Research, 2015, 45(3): 904-926．

[11]Vlasenko V, Stashchuk N, Guo C, et al. Multimodal structure of baroclinic tides in the South China Sea[J]. Nonlinear Processes in Geophysics, 2010, 17(5): 529-543．

[12]Qian H, Huang X, Tian J, et al. Shoaling of the internal solitary waves over the continental shelf of the northern South China Sea[J].Acta Oceanologica Sinica, 2015, 34(9): 35-42．

[13]Zhao W, Huang X, Tian J. A new method to estimate phase speed and vertical velocity of internal solitary waves in the South China Sea[J]. Journal of Oceanography, 2012, 68(5): 761-769．

[14]Alford M H, Lien R-C, Simmons H, et al. Speed and evolution of nonlinear internal waves transiting the South China Sea[J]. Journal of Physical Oceanography, 2010, 40(6): 1338-1355．

[15]Klymak J M, Pinkel R, Liu C-T, et al. Prototypical solitons in the South China Sea[J]. Geophysical Research Letter, 2006, 33(11): 1-4．

[16]Helfrich K R, Melville W. On long nonlinear internal waves over slope-shelf topography[J]. Journal of Fluid Mechanics, 1986, 167：285-308．

[17]Vlasenko V, Hutter K. Generation of second mode solitary waves by the interaction of a first mode soliton with a sill[J]. Nonlinear Processes in Geophysics, 2001, 8(4/5): 223-239．

[18]Chao S Y, Shaw P T, Hsu M K, et al. Reflection and diffraction of internal solitary waves by a circular island[J]. Journal of Oceanography, 2006, 62(6): 811-823．

[19]Stastna M, Peltier W. On the resonant generation of large-amplitude internal solitary and solitary-like waves[J]. Journal of Fluid Mechanics, 2005, 543(1): 267-292．

[20]Mehta A, Sutherland B, Kyba P. Interfacial gravity currents. Ⅱ. Wave excitation[J]. Physics of Fluids, 2002, 14(7):3558-3569．

刘娜，李本霞，王辉，等. 西北太平洋浪流相互作用对有效波高的影响研究[J]. 海洋学报， 2016， 38(9): 21-31， doi:10.3969/j.issn.0253-4193.2016.09.003

Liu Na， Li Benxia， Wang Hui， et al. A study of the influence of wave-current interaction on significant wave height in the Northwestern Pacific[J]. Haiyang Xuebao， 2016， 38(9): 21-31， doi:10.3969/j.issn.0253-4193.2016.09.003

Observational study of one prototypical mode-2 internal solitary waves in the northern South China Sea

Qian Hongbao1，2， Huang Xiaodong1， Tian Jiwei1

(1.KeyLaboratoryofPhysicalOceanography，MinistryofEducation，OceanUniversityofChina，Qingdao266100，China;2.TheAdministrativeCenterforChina’sAgenda21，Beijing100089，China)

Mode-2 internal solitary wave (ISW) is seldom observed in real oceans. In this study， the characteristics of one prototypical mode-2 ISW over the continental shelf of northern South China (SCS) were analyzed， by using of mooring measurements with fine spatial and temporal resolutions. It was shown that the current core of mode-2 ISW appeared at a depth of 135 m， with a maximum of 0.66 m/s. The currents along the ISW propagation direction covered a depth range of 80～170 m， and the currents at a reverse direction were observed near the surface and bottom. Vertical mode analysis revealed that observed vertical structure of horizontal current of ISWs matched well with the theoretical results. At the trough of mode-2 ISW， the depth-integrated horizontal kinetic energy (KE) density could reach 14 kJ/m2. Along the wave front， the KE of mode-2 ISW was up to 5.98 MJ/m. Although the kinetic energy of the mode-2 ISW was one order smaller than that of strong mode-1 ISW， its current shear of up to 0.045 s-1was two times as strong as that of mode-1 ISW， which suggested a more rapid energy dissipation．

internal solitary wave; mode-2; mooring; observation; South China Sea

2016-04-26；

2016-05-13。

南海关键岛屿周边多尺度海洋动力过程研究(2014CB745003)；内波与混合精细化观测系统集成与示范(2013AA09A502)；国家自然科学基金-南海北部内孤立波的季节与年际变化特征及影响机制(41506011)；广东省近海海洋变化与灾害预警重点实验室(GLOD)开放课题(GLOD1403)；青岛博士后应用研究项目。

钱洪宝(1977—)，男，河北省唐山市人，副研究员，主要研究方向为海洋科技管理、物理海洋。E-mail：qhb@acca21.org.cn

黄晓冬(1987—)，男，山东省菏泽市人，讲师，主要从事海洋内波研究。E-mail:xhuang@ouc.edu.cn

P731.2

A

0253-4193(2016)09-0013-08