考虑逆变类分布式电源特性的有源配电网反时限电流差动保护

李　娟　高厚磊　朱国防

(电网智能化调度与控制教育部重点实验室(山东大学)　济南　250061)



考虑逆变类分布式电源特性的有源配电网反时限电流差动保护

李娟高厚磊朱国防

(电网智能化调度与控制教育部重点实验室(山东大学)济南250061)

分析推导了有源配电网电流正序故障分量的分布特征，并基于正序故障分量提出了反时限电流差动保护方案。根据逆变类分布式电源(DG)故障后电流响应特征，建立了有源配电网正序故障分量复合序网，严格推导了保护区段两端电流正序故障分量计算表达式，定性分析了逆变类DG作用下区段两端电流正序故障分量的幅值和相位特征。以此为基础结合配电网特有的结构和参数特点，设计了反时限电流差动保护动作判据和整定方法。最后利用PSCAD建立有源配电网系统模型，对所提动作判据进行了仿真验证。结果表明，该保护方案可以有效区分电动机自起动过程和内部轻微故障，可以在保证对TA饱和足够制动能力的同时，提高保护灵敏度，且对有源配电网中DG出力随机性、馈线结构的多样性等具有较强的适应性。

有源配电网逆变类DG不可测分支电流差动保护反时限

0　引言

分布式电源并网管理办法的制定和完善，促进了可再生能源发电的迅速发展。可再生能源发电将成为未来数十年国内电力供应的重要组成部分[1]。另一方面，可再生能源的大量接入也为电网的安全稳定运行带来了诸多问题，所面临的最大挑战是如何解决可再生能源接入后引起的保护误动或拒动问题[1]。传统配电网为单电源辐射型网络，潮流与故障电流单方向流动，分布式电源的大量接入使其变为多端、多源，潮流与故障电流方向不确定，弱馈问题突出的有源网络[2]。常规三段式电流保护难以保证保护的选择性和灵敏性[3-6]。

分布式电源(Distributed Generation，DG)类型众多，既有可以直接并网的电机类DG，又有经逆变、升压并网的逆变类DG；既有微网运行方式，又有并网运行方式，且具有间歇性、多变性和不确定性。若要保证接入各种类型和模式DG的配电网安全稳定运行，需要完善的保护与控制策略。

为解决上述问题，国内外学者做了大量的研究工作。文献[6-11]分析了不同类型DG故障时的响应情况、等效方法、故障电流计算方法以及DG接入电网后的故障电流分布特征，为有源配电网保护方法的提出奠定了基础。文献[12，13]对距离保护在有源配电网中的应用进行了论证。文献[14]提出了基于故障线路两侧电流幅值差异比较的配电网新型保护方案。文献[15]指出多电源是导致有源配电网故障定位困难的主要原因，并提出了一种有效的解决方案。文献[16-18]分析了故障后保护区段两端电流相角的变化特征，提出了基于故障电流相位变化的过电流保护方案，并讨论了关键技术的解决方法。文献[19，20]提出了基于故障电流突变量相位变化方向的纵联保护方案。文献[21]综合考虑了配电网的特点，提出了一种区域继电保护保护算法。上述算法在理论和技术方面为分布式电源的并网应用奠定了基础。但受目前配电网设备配置情况以及分布式电源不确定性等因素的影响，上述算法仍受以下一个或多个因素的制约：①需要电压信号的配合，而配电网中TV配置率较低，实际应用投资较大；②原理分析时，将DG统一等效为电压源，且忽略逆变类DG接入点电压相位的变化；③仅利用电流的相位信息，在应对含逆变类DG配电网故障时，逆变类DG输出电流的不确定性会降低保护的灵敏度；④配电网多不可测分支，电动机的自起动电流会影响保护动作可靠性。因此，有必要针对上述因素，研究更为完善的保护与控制策略。

电流差动保护同时利用电流的幅值和相位信息，具有绝对选择性。由于正序故障分量(Positive Sequence Fault Components，PSFC)可以反映所有的故障类型，消除负荷对故障电流的影响，降低通信量，保护主要应对两相短路和三相短路情况，作三相重合闸，不需要故障相的判断，因此采用正序故障分量作为保护电气量构成电流差动保护。又考虑到不可测分支电动机自起动电流的衰减特性，本文基于配电网广域测控平台[22，23]，基于正序故障分量提出了反时限电流差动保护方案。主要内容有：分析不同类型DG的故障响应情况，建立DG等效电路模型；建立有源配电网正序故障分量复合序网络模型，分析区段两端电流正序故障分量的幅值和相位关系；根据有源配电网的结构和参数特点，设计反时限电流差动保护动作判据和整定方法；搭建有源配电网系统模型，仿真验证所提差动保护动作判据的可行性。

1　分布式电源故障特征分析

分布式电源种类众多，可分为电机类和逆变类，受控制方式的影响，故障后电流响应也不尽相同。

1)电机类DG。

对于电机类DG，故障瞬间短路电流可达(6～10)IN。由于保护一般只利用故障后1～2周波数据，故将电机类DG统一等效为电压源与内阻抗的串联，如图1a所示。图中UDG为DG等效电压，Zdg为等效内阻抗，与系统电源相比，电机类DG内阻抗较大。

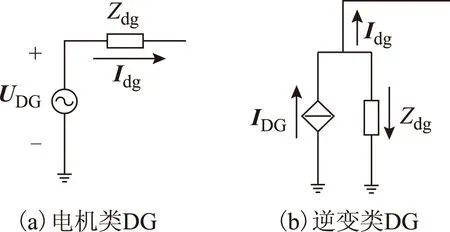
图1　分布式电源的等效电路Fig.1　Equivalent circuit of DG

由于故障前后电机类DG接入点电压相位基本不变，故障后输出电流滞后于接入点电压的角度约等于线路阻抗角，由系统电源与电机类DG分别作用产生的短路电流相位基本一致。

2)逆变类DG。

逆变类DG受控制策略的影响，故障后DG对外输出电流最大不超过1.2(pu)～2(pu)，可将其等效为一电流源与阻抗的并联，如图1b所示。图中，IDG用于等效不受最大幅值限制时DG的输出电流，Idg为受幅值限制时DG对外输出电流，相位与接入点参考电压的夹角受电压跌落程度的影响；Zdg为逆变类DG等效阻抗，用于等效因限制最大输出电流所采取的策略(如卸荷电路等)，受故障点位置、过渡电阻等因素影响，是可变的。

现有并网规定要求接入中压配电网的逆变类DG具有一定的低压穿越能力。当电压跌落后仍在(0.2～0.9)UN范围内时，DG需保持并网并输出一定的无功功率以起到电压支撑的作用。逆变类DG在低电压穿越运行期间向电网提供的有功Id和无功Iq电流(电流幅值低于最大允许值时)可表示为[24]

(1)

Iq=1.5(0.9-γ)IN0.2≤γ≤0.9

(2)

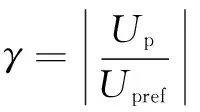
逆变类DG输出电流幅值和功率因数角可表示为[24]

(3)

(4)

当按式(1)、式(2)计算所得短路电流的幅值大于电流最大允许值时，则以保证DG对电压的最大支撑作用为第一目标，将有功电流变为

(5)

式中，Immax为逆变类电源所允许流过电流的最大幅值。

假设正常情况下，DG接入点电压为额定电压，输出电流为额定电流，Immax取2(pu)，则由式(1)～式(3)可以推出逆变类DG输出最大电流所对应电压跌落系数γ1为0.521 5。当γ>γ1时，DG输出电流IDG小于最大幅值，逆变类DG对外输出电流Idg与DG输出电流IDG相等，并联阻抗Zdg上无分流，Zdg为无穷大，可将逆变类DG可等效为一个压控电流源，由式(1)、式(2)可得DG输出电流的幅值和相位为

(6)

a=arctan(1.5γ(0.9-γ)

(7)

进而推出当γ∈[0.5215，0.9]时，DG输出电流的幅值范围为1.12(pu)～2.0(pu)，相位滞后于接入点电压0°～17°，并随电压跌落程度的增加而增加。

当γ<γ1时，IDG随电压跌落程度的增加，幅值由2.0(pu)增加到5.1(pu)，电流相位滞后接入点电压11.7°～17°。但DG对外输出电流Idg由式(2)、式(5)决定，幅值始终为2(pu)，可将其等效为一个恒流源，相位滞后接入点电压17°～31°。此时Idg≠IDG，流经Zdg上的电流即为限流措施上的分流。又因为Idg与IDG中无功分量相等，Zdg上的分流为纯阻性电流，用于消耗故障前后电源输出有功功率差，大小受γ影响，是可变的。这与文献[25]所提及卸荷电路的阻抗特性一致。

结合上述假设条件，可以推出，极端情况下DG对外输出最大无功功率仅能达到视在功率的52.5%，在现有并网规定下逆变类DG不能只输出无功功率。以接入点电压为0°，则逆变类DG输出电流IDG与对外输出电流Idg的幅值和相位关系如图2所示。

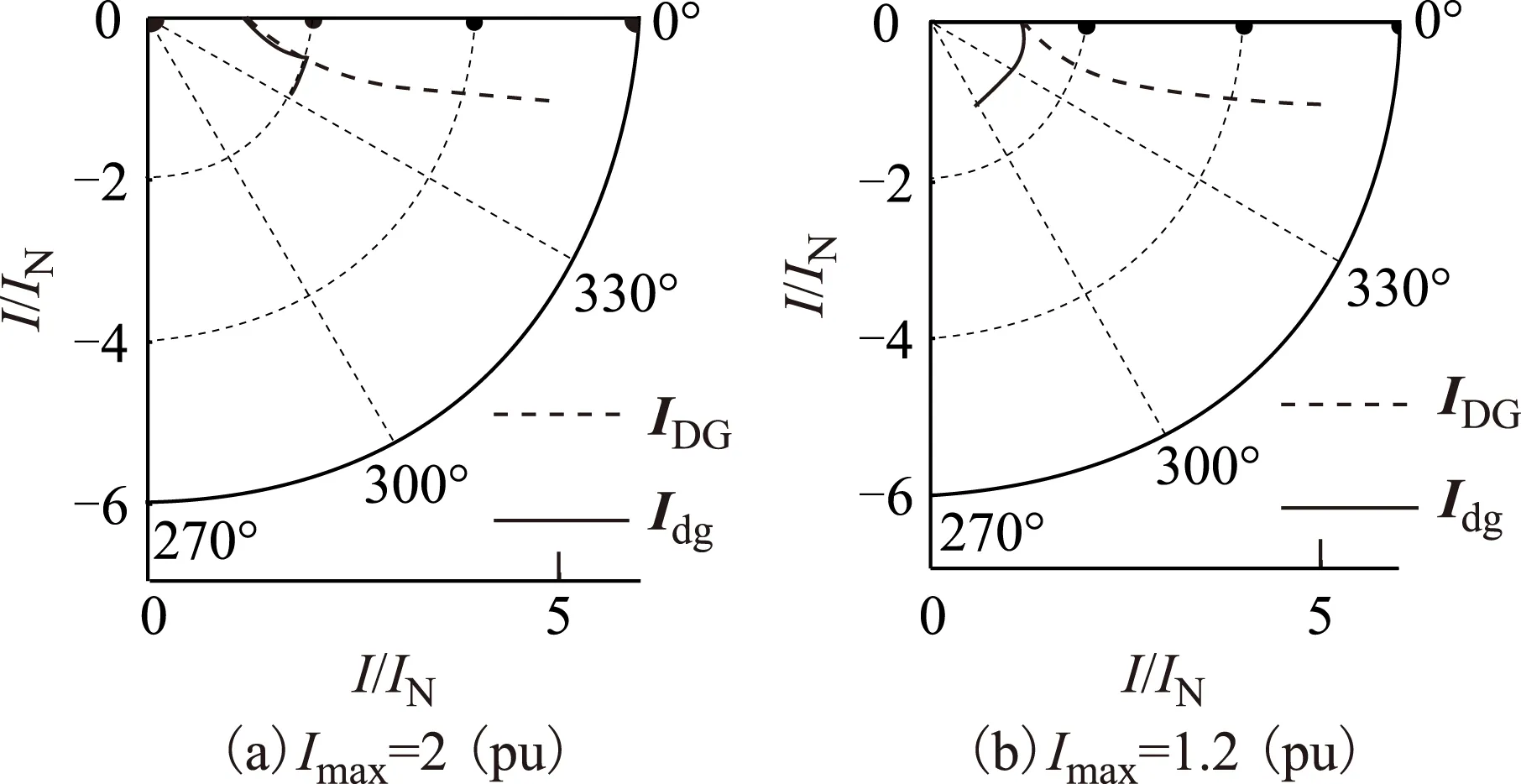
图2　逆变类DG 输出电流与对外输出电流Fig.2　Internal and external current of IIDG

当Immax取1.2(pu)，γ2=0.863。当γ>γ2时，DG输出电流的幅值范围为1.1(pu)～1.2(pu)，相位滞后于接入点电压0°～5.0°；当γ<γ2时，IDG幅值由1.2(pu)增加到5.1(pu)，电流相位滞后接入点电压5.0°～16.9°；Idg幅值始终为1.2(pu)，相位滞后接入点电压5.0°～61.1°。

综上所述，故障后逆变类DG对外输出电流受电压跌落程度和接入点电压相位的影响。不同于电机类DG，逆变类DG接入点电压相位在故障后会发生突变，这是因为逆变类DG的控制始终跟踪接入点电压正序分量，而故障后电压正序分量的相位受故障类型、过渡电阻以及线路阻抗的影响，会发生突变。可见，逆变类DG的输出电流相位具有不确定性。

2　有源配电网电流正序故障分量分布

电流差动保护区段两端电流的相位差会直接影响保护的整定计算以及灵敏度。而逆变类DG输出电流的不确定性主要受接入点电压相位的影响。参考图3，根据故障点发生的位置，可分两种情况进行讨论:①当f1点发生短路故障时，DG接入点电压将失去钳制，接入点电压相位会发生变化；②当故障发生在f2点时，DG接入点电压相位依然受系统电压钳制，接入点电压相位基本不变。本文主要讨论第一种情况。

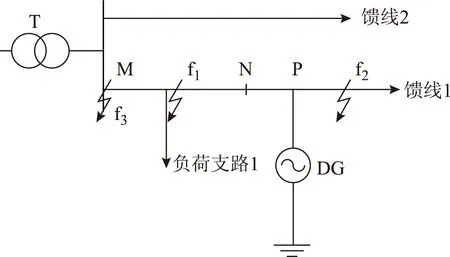
图3　含分布式电源接入的简单配网结构Fig.3　Distribution network with DG integrated

逆变类DG输出电流由电力电子器件控制，故障瞬间即可完成突变，因此认为逆变类DG仍满足叠加原理，在故障附加网络中用电流源来等效，幅值为故障前后逆变类DG输出电流的变化量。则以图3简单拓扑网络为例，假设f1点发生故障，又因为馈线上负荷等效阻抗远大于变压器阻抗，则其正序故障分量复合序网如图4所示。

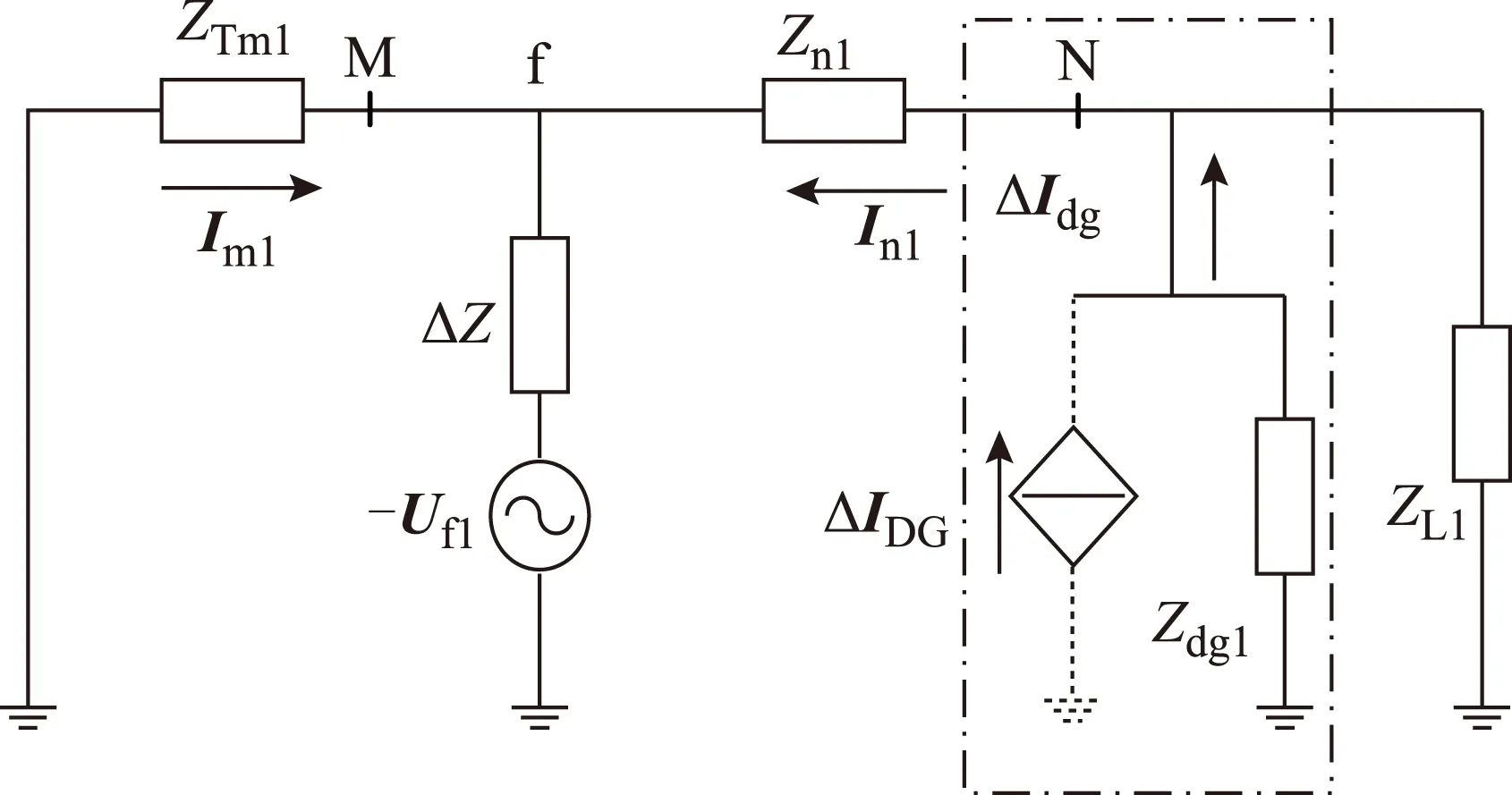
图4　简化的正序故障分量复合序网Fig.4　Simplified positive-sequence fault component complex network of short-circuit fault

图中，-Uf1为正序故障分量虚拟电源；点划线框内为逆变类DG等效电路，其中ΔIDG为不考虑限流策略时DG输出电流的变化量；ΔIdg为DG向电网输出电流的变化量；ΔIm1、ΔIn1分别为保护区段两端检测点M、N电流正序故障分量；ZTm1为故障点到电源的等效阻抗；ZL1为分布式电源下游线路和负荷的正序阻抗；Zn1为故障点分支电源间正序阻抗；Zdg1为分布式电源的正序阻抗；ΔZ为附加阻抗，与故障类型有关。

当DG为电机类时，则以内阻抗Zdg1等效，可认为是图4的特殊情况，则在忽略负荷阻抗ZL1后，保护区段两端电流正序故障分量的相位与ZTm1和Zn1+Zdg1的阻抗角有关。以架空线路(线路阻抗角为72°)为例，保护区段两端电流正序故障分量的夹角φmn约为

φmn∈(0°，18°)

即当保护区段两端分别由电机类DG和系统电源提供电流时，两端电流相位差较小。

当DG为逆变类DG时，根据叠加原理，图4中保护区段两端检测点的电流由两部分构成：一部分由虚拟电源产生；一部分由逆变类DG等效电流源产生。对于电流源支路，外电路为负荷阻抗ZL1与DG接入点上游等效阻抗的并联，则忽略ZL1上的分流，两端电流的正序故障分量可表示为

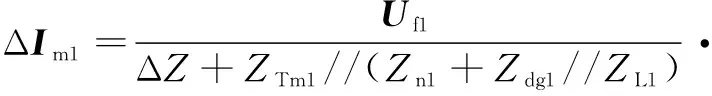
(8)

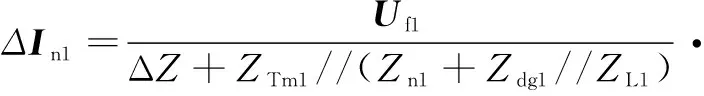
(9)

对于虚拟电源支路，由于内阻抗Zdg1对外表现为无穷大，外电路阻抗为ZTm1//(ZL1+Zn1)，忽略故障点下游等效阻抗，式(8)、式(9)可简化为

(10)

ΔIn1=ΔIdg

(11)

根据逆变类DG输出电流的大小，分两种情况讨论区段两端电流正序故障分量幅值和相位关系。

1)逆变类DG输出电流大于2倍额定电流。

以三相短路为例，假设DG额定电流小于等于该馈线额定电流，则当DG输出电流小于2倍额定电流时，故障点到DG接入点电压降最大不超过20%。若要使DG接入点电压跌落系数为0.2～0.521 5，则过渡电阻不为0。又因为线路上压降有限，因此故障点电压较大，相位上滞后系统电压0～90°，进而推出DG接入点电压滞后系统电压0～90°。则区内故障两端检测点电流正序故障分量相量域如图5所示。

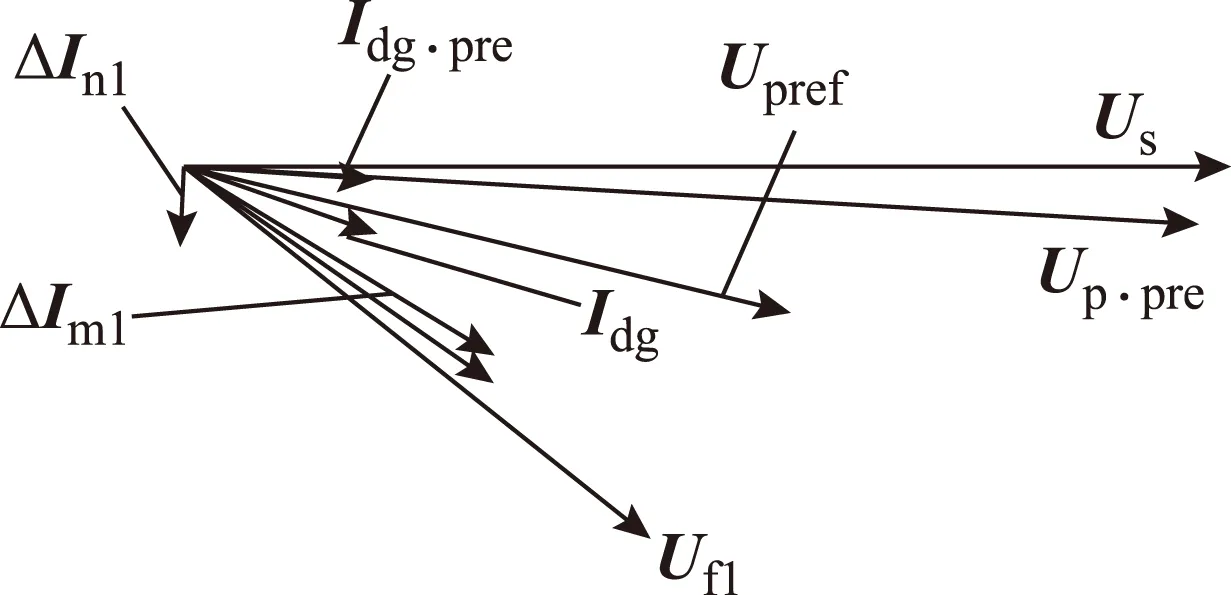
图5　区内故障两端检测点电流正序故障分量相量域Fig.5　PSFC phasor of detection points with internal fault

图5中Us为系统电压；Uf1为故障点电压；Up.pre为故障前DG接入点电压；Upref为故障后DG接入点电压；Idg.pre为故障前DG输出电流。

假设此时系统电源提供的短路电流随过渡电阻的大小，变化范围是6(pu)～12(pu)，根据式(10)、式(11)可以推出

arg(ΔIm1)∈(-147.8°,-91.1°)

arg(ΔIn1)∈(-118.8°,-73.4°)

进而推出，当保护区段两端短路电流分别由系统电源和逆变类电源提供时，两端电流正序故障分量的夹角φmn1约为

φmn1∈(0°，75°)

2)逆变类DG输出电流小于2倍额定电流。

当DG输出电流较小，可能是过渡电阻较大，或者故障点距DG接入点较大，假设此时系统电源提供的短路电流随过渡电阻的大小，变化范围是3(pu)～12(pu)，系统电压为0°，则可以推出

arg(ΔIm1)∈(-147.8°,-18.1°)

arg(ΔIn1)∈(-118.8°,-18.1°)

可以推出，当保护区段两端短路电流分别由系统电源和逆变类电源提供时，两端电流正序故障分量的夹角φmn2范围约为

φmn2∈(0°，130°)

同理，当发生两相短路故障时，亦存在两端电流正序故障分量相角相差较大的结论。

由此可见，对于含DG的有源配电网，由于逆变类DG故障后接入点电压相位以及电流相位的不确定性，导致仅利用相位信息保护方案具有局限性，因此本文采用电流差动保护方案，同时利用幅值和相位信息，以提高保护对不同故障情况的适应性。

3　不可测分支的影响

不同于输电网，配电网结构复杂，设备配置不齐，需额外考虑不可测分支。对于非故障区段，不可测分支上的电流即为两端电流差流。虽然馈线上的分支有电源分支和负荷分支，但考虑到大中型分布式电源均装设保护装置，本节主要分析不可测负荷分支的情况。

1)非故障区段不可测分支分流对保护的影响。

当故障点位于保护区段下游时，各检测点与不可测分支负荷上电流正序故障分量分布图6所示。

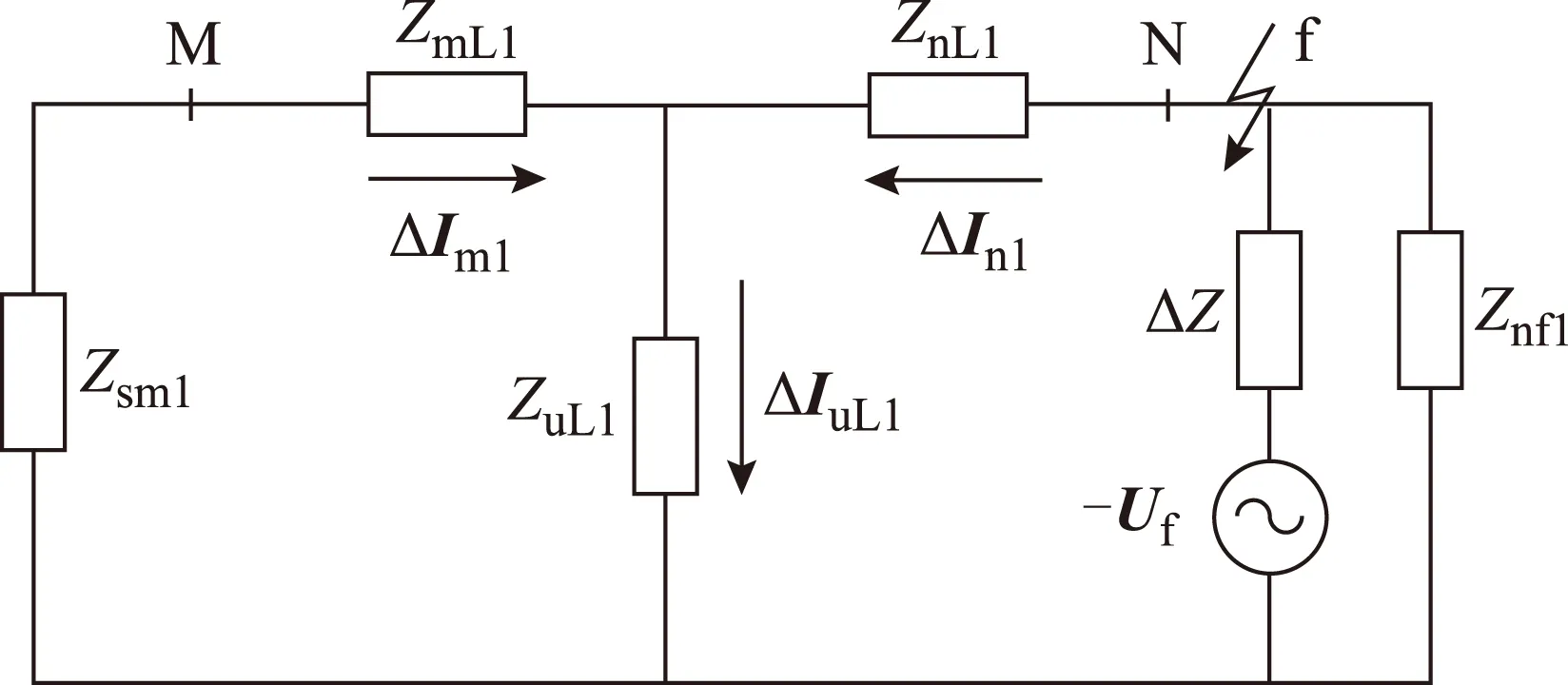
图6　区外故障不可测分支的影响Fig.6　Impact of non-measurable branch with a downstream external fault

图6中，Zsm1为电源到检测点M的等效阻抗；ZuL1为不可测分支负荷的正序阻抗；ZmL1为检测点M到分支负荷的正序阻抗；ZnL1为检测点N到分支负荷间正序阻抗；Znf1为故障点下游正序等效阻抗；ΔIuL1为流经分支负荷电流的正序故障分量。

由图6可得出

(12)

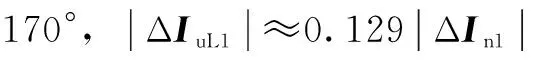
当故障点位于保护区段上游，各检测点与不可测分支负荷上电流正序故障分量分布如图7所示。

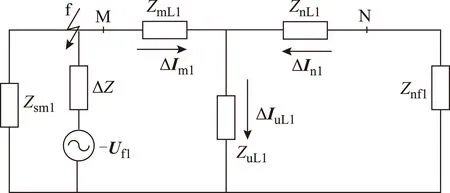
图7　区外故障不可测分支的影响Fig.7　Impact of non-measurable branch with an upstream external fault

区段两端电流正序故障分量为

(13)

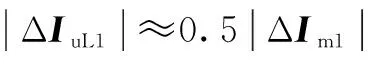
可见，不可测分支分流对电流幅值的影响较大，对相位影响较小，存在两端电流相位始终接近180°的特点。

2)正常运行时，负荷投切对保护的影响。

正常情况下，负荷投切时，两端差流为负荷分支电流。该负荷分支电流的大小与负荷性质密切相关。当负荷分支上存在电动机时，负荷的瞬间投入会导致较大的电动机自起动电流。又因为工业用大型电动机多通过专线上网，一般可测，因此在保护判据整定过程中，主要考虑中小型电动机自起动电流对保护的影响。

4　保护动作判据设计

与输电网不同，配电网直接面向用户，负荷频繁波动，且峰谷差较大，为防止保护装置的频繁起动，本文结合电流差动保护绝对选择性的特点，以最大不可测分支的额定电流设计起动方程

(14)

式中，kset1为保护起动系数，按考虑非周期分量的影响及TA检测误差等因素整定，为保证轻微故障保护动作灵敏度，此处不考虑电动机自起动系数，可取1.2～1.3；IuLN为该保护区段最大不可测负荷分支额定电流。

由式(14)可以看出，保护起动方程无法从幅值上区分电动机的自起动与轻微故障。而反时限电流保护的动作时间随故障电流的增大而降低，具有自适应反应故障严重程度以及区分电动机自起动过程的能力。因此本节考虑引入反时限电流保护。又考虑到逆变类DG输出电流的不确定性以及非故障区段不可测负荷分支电流的幅值和相位特征，选择以幅值和相位信息构成独立约束判据，最大限度地增大动作区，则基于正序故障分量的反时限电流差动保护动作方程为

(15)

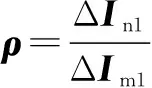
判据式(15)中差动保护判据ρ-平面动作特性如图8所示。

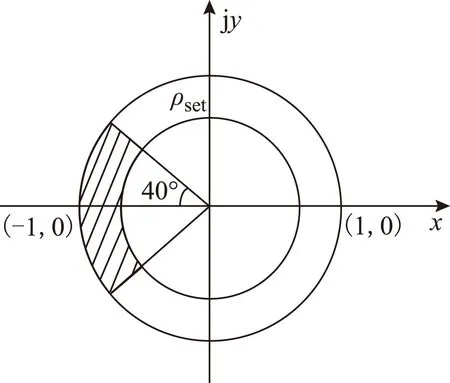
图8　反时限差动保护动作特性Fig.8　Operation characteristic of inverse-time current differential protection

对于反时限方程参数中时间常数k的整定主要考虑电动机自起动电流的衰减时间以及与保护的动作时限要求，反时限曲线形状系数α与曲线平移系数β的整定参照非常反时限曲线，分别取2和1。

对于幅值判据ρset的整定主要是考虑非故障区段不可测分支分流，TA检测误差和一定的裕度等因素取0.7。

对于相位判据的整定，结合常规比例制动判据最大相移制动能力(150°)、区外故障不可测分支负荷上分流对相位的影响、TA检测误差和裕度角等因素时，相位判据选为140°。

结合图8可以看出：

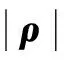
4)对于区外故障，电流互感器严重饱和的情况，通过相位判据可以有效应对。

5)对于含不可测分支的非故障区段，两端电流正序故障分量的相位差约为180°，最大幅值比约为0.5，保护可靠不误动。

6)对于不可测分支电动机自起动的情况，虽然差动保护判据可以满足，但受保护反时限方程的限制，保护可靠不误动。

5　电流差动保护数据同步方案

故障数据同步是电流差动保护应用需要解决的关键技术之一。由于配电网没有架设专用对时信道且网架结构复杂、多变，现有高压输电网中应用较为成熟的对时同步方法不能直接应用于配电网中。根据配电网特点，可以采用基于故障时刻的故障数据自同步方法[27]，不需要增加额外成本，有利于电流差动保护的推广及应用，其工作原理如下：当配电线路发生故障时，故障点虚拟电源会产生电磁波，并由故障点向线路两端传播，两端保护起动元件经一定延时后检测到线路发生了故障。当忽略电磁波在线路上的传播时间(配电线路较短，电磁波传播时间短)，两端保护装置的故障检测延时(保护起动元件检测到故障的时刻和真正故障时刻的时间差)时间差在允许范围内时，可以认为两端保护装置检测到的故障时刻为同一时刻，标记该时刻，并以该时刻为对时同步标准，可实现故障数据的近似同步。

由此可以看出，通过故障时刻的准确识别，并以故障时刻作为对时同步标准时刻，即可实现故障数据的近似同步，进而实现电流差动保护在配电网中的应用。

6　仿真分析

6.1仿真模型

利用PSCAD软件建立有源配电网模型，其模型结构如图3所示。变压器容量为50 MV·A，变压器电压比为110/10.5 kV，YNd11接法，负载损耗182.44 kW，短路阻抗16.64%，空载损耗30.95 kW，空载电流0.140%。其线路参数为：R=0.13 Ω/km，X=0.402 Ω/km。馈线1的线路长度为20 km，馈线2的线路长度为6 km。保护检测点M位于母线处，N距母线10 km，DG接于馈线1，距母线14 km，容量为3.6 MW。馈线1上负荷分支load1距母线4 km，容量为3.6 MW；末端负荷大小为3.6 MW。假设电流方向由节点流向线路为正。区内故障点f1点距母线4 km，区外故障点f2距母线17 km，故障点f3距母线100 m。

保护区段内不可测负荷分支电流的幅值约为260 A，则保护起动门槛约为310 A。

6.2仿真数据

1)区内故障。

通过在f1点设置不同故障类型和故障电阻，得到的仿真结果见表1。

由表1可以看出，逆变类DG接入点电压相位会发生突变。而接入点电压相位的不确定性直接导致了DG输出电流相位的不确定，可能出现故障区段两侧检测点电流正序故障分量夹角较大的情况。如发生两相短路时，两端电流正序故障分量较大，此时仅依靠相位信息进行故障判断会出现灵敏度低的情况。

表1　区内故障仿真表Tab.1　Simulation data with internal fault

本文所提反时限电流差动保护算法在不同故障类型、不同过渡电阻的区内故障情况下，均能够可靠动作，具有较强的适应性。

2)区外故障。

通过在f2和f3点设置不同故障类型和故障电阻，得到的保护区段两端电流正序故障分量仿真结果见表2。

从表2中可以看出，当故障点位于保护区段下游时，不可测分支负荷上的分流较小，两端电流幅值基本相等，相位接近反向；当故障点位于保护区段上游时，不可测负荷分支上的分流较大，两端幅值相差较小，相位接近180°，该仿真结果与理论分析基本一致。本文所提出反时限电流差动保护在不同故障点、不同过渡电阻情况下，均能够正确判断为区外故障。

3)负荷投切。

以不可测分支(负荷分支1)上不同容量电动机自起动为例进行验证，保护区段两端电流正序故障分量仿真数据见表3。

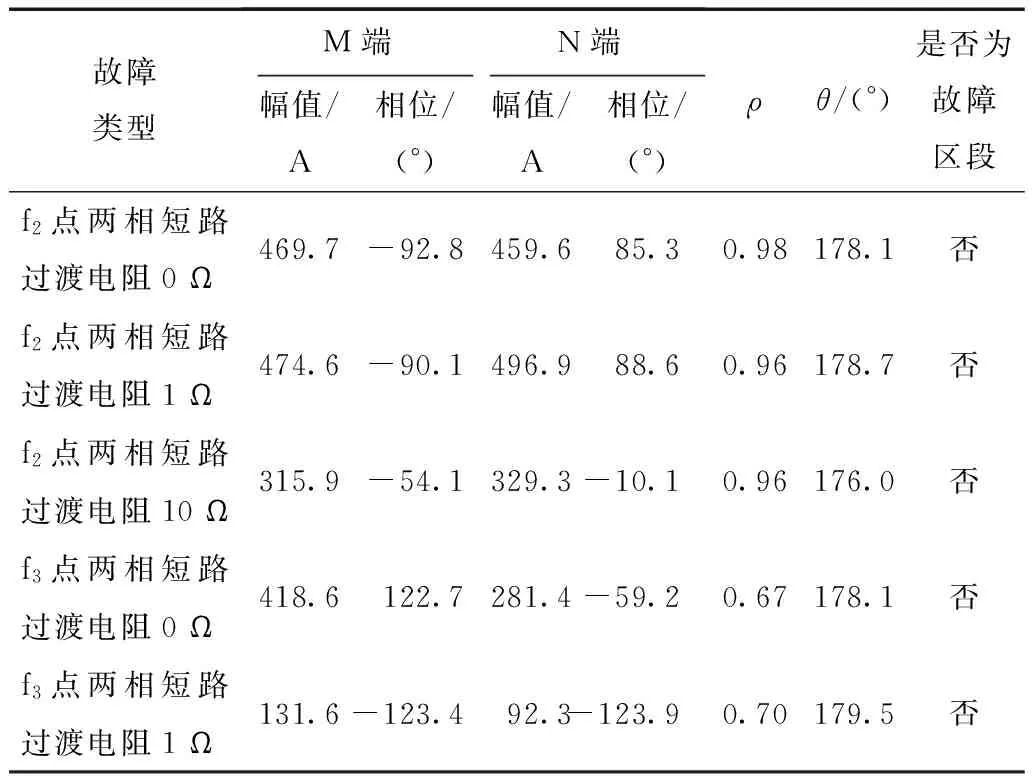
表2　区外故障仿真表Tab.2　Simulation data with external fault

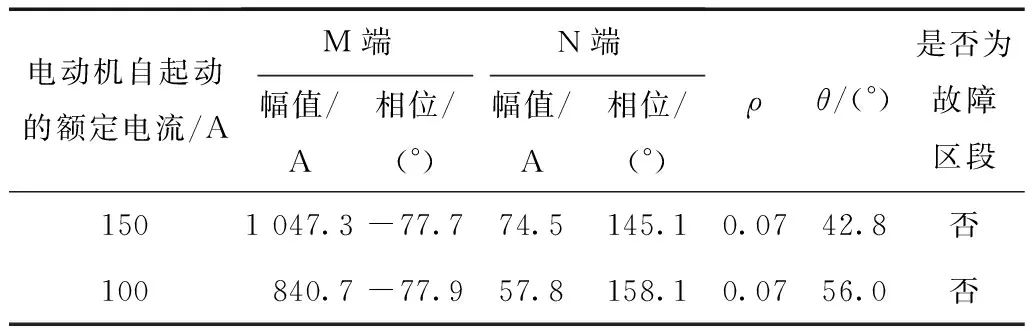
表3　负荷投切仿真表Tab.3　Simulation data with load switching

结合表3数据和电动机自起动电流衰减时间(约为0.1 s)以及与其他保护(熔断器等)的时间配合，查询非常反时限曲线，确定k取0.18。此时即使保护起动，也可以保证保护可靠不动作。

综上所述可以得出，该反时限电流差动保护同时利用电流的幅值和相位信息，可以有效应对逆变类DG输出电流不确定性对保护的影响，且灵敏度较高，具有较强的适应性。

7　结论

本文结合有源配电网独特的网络结构和参数特点，提出了基于正序故障分量的反时限电流差动保护算法，经理论分析和仿真验证，可以得到以下结论：

1)故障后逆变类DG所提供短路电流的相位受接入点电压相位和电压跌落系数的影响，具有不确定性。

2)当保护区段两端分别由系统电源和逆变类DG提供短路电流时，某些情况下存在保护区段两端电流正序故障分量相位差较大的情况，当为电机类DG时，相位差较小。

3)配电网中多分支，对于非故障区段不可测分支的分析结果表明，分支负荷上会出现较大分流，但保护区段两端电流相位差始终接近180°。

4)本文根据电动机自起动电流会衰减的特征，将反时限过电流保护与电流差动保护相结合构成反时限电流差动保护，并给出了相应的保护判据整定方法。该方法不需要电压信息，可以有效应对未来电网DG大量接入的情况，且具有灵敏度高，受负荷分支、DG随机、分散接入的影响较小的优点。

5)仿真结果表明，该反时限电流差动保护具有较强的适应性。

[1]余贻鑫，刘艳丽.智能电网的挑战性问题[J].电力系统自动化，2015，39(2)：1-5.

Yu Yixin，Liu Yanli.Challenging of smart grid[J].Automation of Electric Power Systems，2015，39(2)：1-5.

[2]高厚磊，李娟，朱国防，等.有源配电网电流差动保护应用技术探讨[J].电力系统保护与控制，2014，42(5)：40-44.

Gao Houlei，Li Juan，Zhu Guofang，et al.Study on application technology of current differential protection in active distribution network[J].Power System Protection and Control，2014，42(5)：40-44.

[3]黄泽华，李锰，刘裕涵，等.智能配电网自愈控制方案研究[J].电工技术学报，2014，29(增1)：492-496.

Huang Zehua，Li Meng，Liu Yuhan，et al.Research of smart distribution network self-healing scheme[J].Transactions of China Electrotechnical Society，2014，29(S1)：492-496.

[4]王江海，邰能灵，宋凯，等.考虑继电保护动作的分布式电源在配电网中的准入容量研究[J].中国电机工程学报，2010，33 (20)：37-43.

Wang Jianghai，Tai Nengling，Song Kai，et al.Penetration level permission of for DG in distributed network considering relay protection[J].Proceedings of the CSEE，2010，33(20)：37-43.

[5]曹贵明.基于正序故障分量的含分布式电源配电网保护研究[D].重庆：重庆大学，2012.

[6]Baran M E，El-Markaby I.Fault analysis on distribution feeders with distributed generators[J].IEEE Transactions on Power Systems，2005，20 (4)：1757-1764.

[7]Fischer M，Mendonça A.Representation of variable speed full conversion Wind Energy Converters for steady state short-circuit calculations[C]//IEEE Power Engineering Society Transmission and Distribution，San Diego，CA，2012:1-7.

[8]吴争荣，王钢，李海峰，等.计及逆变型分布式电源控制特性的配电网故障分析方法[J].电力系统自动化，2012，36(18)：92-99.

Wu Zhengrong，Wang Gang，Li Haifeng，et al.Fault characteristics analysis of distribution networks considering control scheme of inverter interfaced distributed generation[J].Automation of Electric Power Systems，2012，36(18)：92-99.

[9]吴争荣，王钢，李海峰，等.含分布式电源配电网的相间短路故障分析[J].中国电机工程学报，2013，33(1)：130-138.

Wu Zhengrong，Wang Gang，Li Haifeng，et al.Analysis on the distribution network with distributed generators under phase-to-phase short-circuit faults[J].Proceedings of the CSEE，2013，33(1)：130-138.

[10]Boutsika T N，Papathanassiou S A.Short-circuit calculations in networks with distributed generation[J].Electric Power Systems Research，2008，78 (11)：1181-1191.

[11]Morren J，de Haant S W H.Impact of distributed generation units with power electronic converters on distribution network protection[C]//IET Developments in Power System Protection，Glasgow，Scotland，2008:664-669.

[12]Huang Wentao，Tai Nengling，Zheng Xiaodong，et al.An impedance protection scheme for feeders of active distribution networks[J].IEEE Transactions on Power Delivery，2014，29(4)：1591-1602.

[13]谷松林.基于广域保护系统的距离后备保护整定方案[J].电力系统保护与控制，2016，44(1)：40-47.

Gu Songlin.A distance backup protection setting scheme based on wide area protection system[J].Power System Protection and Control，2016，44(1)：40-47.

[14]许偲轩，陆于平.含 DG 配网电流幅值差异化保护方案[J].电工技术学报，2015，30(18)：164-170.

Xu Sixuan，Lu Yuping.Current amplitude differential protection for distribution system with DG[J].Transactions of China Electrotechnical Society，2015，30(18)：164-170.

[15]Rezaei N，Haghifam M.Protection scheme for a distribution system with distributed generation using neural networks[J].International Journal of Electrical Power & Energy System，2008，3(3)：235-241.

[16]Ukil A，Deck B，Shah V H.Current-only directional overcurrent protection for distribution automation challenges and solutions[J].IEEE Transactions on Smart Grid，2012，3(4)：1687-1794.

[17]Ukil A，Deck B，Shah V H.Current-only directional overcurrent relay[J].IEEE Sensors Journal，2011，11(6)：1403-1404.

[18]Ukil A，Deck B，Shah V H.Smart distribution protection using current-only directional overcurrent relay[C]//IEEE Power Engineering Society Innovative Smart Grid Technologies，Gothenburg，Sweden，2010：1-7.

[19]El Halabi N，García-Gracia M，Borroy J，et al.Current phase comparison pilot scheme for distributed generation networks protection[J].Applied Energy，2011，88：4563-4569.

[20]司新跃，陈青，高湛军，等.基于电流相角突变量方向的有源配电网保护[J].电力系统自动化，2014，38(11)：97-103.

Si Xinyue，Chen Qing，Gao Zhanjun，et al.Protection scheme for active distribution system based on directions of current phase angle variation[J].Automation of Electric Power Systems，2014，38(11)：97-103.

[21]沈鑫，曹敏.分布式发电接入主动配电网区域保护算法[J].电工技术学报，2015，30(1)：352-357.

Shen Xin，Cao Min.Research on regional protection algorithm of distributed generation integration to active distribution network[J].Transactions of China Electrotechnical Society，2015，30(1)：352-357.

[22]程云峰，张欣然，陆超.广域测量技术在电力系统中的应用研究进展[J].电力系统保护与控制，2014，42(4)：145-153.

Cheng Yunfeng，Zhang Xinran，Lu Chao.Research progress of the application of wide area measurement technology in power system[J].Power System Protection and Control，2014，42(4)：145-153.

[23]徐丙垠，薛永端，李天友，等.智能配电网广域测控系统及其保护控制应用技术[J].电力系统自动化，2012，36(18)：2-9.

Xu Bingyin，Xue Yongduan，Li Tianyou，et al.A wide are measurement and control system for smart distribution grids and its protection and control application[J].Automation of Electric Power Systems，2012，36(18)：2-9.

[24]国家电网公司.Q/GDW 617-2011光伏发电站接入电网技术规定[S].2011.

[25]毕天姝，刘素梅，薛安成，等.逆变型新能源电源故障暂态特性分析[J].中国电机工程学报，2013，33(13)：165-171.

Bi Tianshu，Liu Sumei，Xue Ancheng，et al.Fault characteristics of inverter-interfaced renewable energy sources[J].Proceedings of the CSEE，2013，33(13)：165-171.

[26]朱国防，陆于平.扇环型制动区差动保护算法[J].电工技术学报，2009，24 (11)：172-177.

Zhu Guofang，Lu Yuping.A novel differential protection with sector-ring restraint region[J].Transactions of China Electrotechnical Society，2009，24 (11)：172-177.

[27]徐丙垠，王敬华，王亮，等.利用故障信号自同步实现闭环网故障定位的方法：中国,CN102981103A[P].2013-03-20.

Inverse-Time Current Differential Protection in Active Distribution Network Considering Characteristics of Inverter-Interfaced Distributed Generations

Li JuanGao HouleiZhu Guofang

(Key Laboratory of Power System Intelligent Dispatch and Control of Ministry of Education Shandong UniversityJi’nan250061China)

The positive-sequence fault components (PSFC) in the distribution network are analyzed and an inverse-time current differential protection scheme using the PSFC is discussed.According to the current responses of distributed generations (DGs) during fault，positive-sequence fault component complex network of short circuit fault is established.Secondly，the PSFC currents of two monitoring points of protection section are inferred rigorously.And the amplitude and phase characteristics of the PSFC current distribution are invested qualitatively.Combining with the configuration and parameters of the distribution networks，the inverse-time differential protection criterion and setting principle are proposed.Finally，simulations modeled by PSCAD are used to verify the effectiveness of the proposed protection criterion.Simulation results demonstrate that：(1) the scheme presented in this paper can distinguish motor self-starting and slight fault efficiently.(2) it can also solve the contradiction between enough ability for braking saturation current of the current transformer and improving sensitivity to internal faults.(3) it can adapt to multiple situations，e.g.output randomness of DG，variety configuration of feeders.

Active distribution network，inverter-interfaced distributed generations，unmonitored branch，current differential protection，inverse-time

2016-01-22改稿日期2016-04-14

TM773

李娟女，1987年生，博士研究生，研究方向为有源配电网保护与控制。

E-mail：lijuandan@126.com

高厚磊男，1963年生，教授，博士生导师，研究方向为电力系统保护与控制。

E-mail：houleig@sdu.edu.cn(通信作者)

国家高技术研究发展(863)计划重点项目(2012AA050213)、国家自然科学基金(51177096)和国网山东省电力公司科技项目(SGSDWF00YJJS1400563)资助。