基于多代理系统的微电网多尺度能量管理

贾星蓓　窦春霞　岳　东　徐式蕴

(1.燕山大学电气工程学院　秦皇岛　066004 2.南京邮电大学先进技术研究院　南京　210023 3.中国电力科学研究院　北京　100192)



基于多代理系统的微电网多尺度能量管理

贾星蓓1窦春霞1岳东2徐式蕴3

(1.燕山大学电气工程学院秦皇岛066004 2.南京邮电大学先进技术研究院南京210023 3.中国电力科学研究院北京100192)

对基于多代理系统的微电网能量管理策略进行了研究。首先，建立三层多代理系统；然后，基于博弈论研究大电网与多个微电网之间的上层电力市场竞价策略；进而，以单个微电网为研究对象，考虑需求侧响应，研究制定多时间尺度的分布式发电调度策略；最后，考虑到调度策略需要有负荷和风力发电机组短期预测作为前提保障，所以运用混沌相空间预测算法对负荷和风力发电机组进行短期预测。仿真结果验证了所提能量管理策略的有效性。

多代理系统微电网多时间尺度能量管理电力市场竞价策略

0　引言

近年来，微电网的研究受到了国内外学者的广泛关注[1-3]。传统的集中方法已经很难对微电网进行有效、灵活的运行控制和能量管理。多代理系统(Multi-Agent-System，MAS)是由多单元功能智能体形成的松散耦合的网络结构，这些智能体在物理上或逻辑上是分散的，其行为是自治的，它们遵守某种协议而连接起来，通过交互与协作能高效解决复杂系统的控制和管理问题[4，5]。因此，多代理系统被推崇应用到微电网能量管理系统中[6，7]。

为了使电力系统发用电效益最大化，合理的电力市场竞价策略至关重要。目前，竞价策略大致分为以下几种：①市场优化方法，即按照电力市场的结构和交易模式构造模型，在满足系统约束条件下以市场买电费用最小、自身获利最大为双重目标进行优化求解的方法[8]，但是此类方法有违电力市场寡头垄断的特点，所以需要改进；②基于博弈论的方法[9，10]，是基于博弈论收益矩阵，或是基于各种非完全竞争博弈模型进行博弈；③估计竞争者的竞价行为方法[11，12]，一般采用概率分析方法。本文将博弈论的方法和估计竞争者的竞价行为方法相结合来研究电力市场竞价策略。

传统的微电网能量调度策略一般是以微电网的视角对发电机组进行调度，以确定需求侧和分布式能源发电量[13，14]，而没有从需求侧的角度去考虑，遵循的是传统的“发电跟踪负荷”的思路。未来电网运行控制需要改变这一思路，将传统的发电调度改变为考虑需求侧响应的调度策略[15，16]，使其更加经济、灵活。本文考虑需求侧响应，研究制定多时间尺度的微电网能量调度策略。

为了有效解决微电网能量管理问题，本文建立了三层多代理系统。以整个电网的视角，基于博弈论研究构建电力市场日交易竞价模型，采用纳什均衡理论进行求解最优竞价策略。然后以单个微电网为研究对象，构建日内计划和实时计划，即多时间尺度下的目标函数与约束，并且在构建日内计划的目标函数时，基于分时电价不同时间段执行不同电费标准的电价制度，并将需求侧响应也考虑进去。运用混沌相空间预测算法对负荷和风力发电机组进行短期预测，最终得到微电网各分布式发电源的最优调度策略。本文通过仿真研究验证了所提方案的有效性。

1　多代理系统模型

多代理系统具有自主性、交互性、主动性等特点。每个代理具有自治能力，而多个代理形成多代理系统为了完成一个任务或达到一些目的遵守某种协议，来解决远超越单个代理的系统性问题。由于微电网电力市场竞价和内部能量优化管理中数据冗余而导致不够灵活和效率低等原因，本文将利用多代理系统力争高效解决微电网能量管理问题。

首先建立三层多代理系统，如图1所示。第1层代理是电力市场管理系统代理(Market Operators Agent，MOA)；第2层代理是各个参与竞价的微电网代理(Micro-Grid Agent，MGA)和大电网代理(Utility Grid Agent，UGA)；第3层代理是微电网中的分布式电源代理(Distributed Generation Agent，DGA)和负荷代理(Load Agent，LA)。第1、2层代理协调控制的主要任务是微电网电力市场最优竞价，如图2所示；第2、3层代理协调控制的主要任务是基于多时间尺度的微电网内部能量优化分配。通过微电网电力市场最优竞价策略可以得出日微电网最优竞价电量和电价，所得到的数据将用于基于多时间尺度的微电网内部能量优化分配。

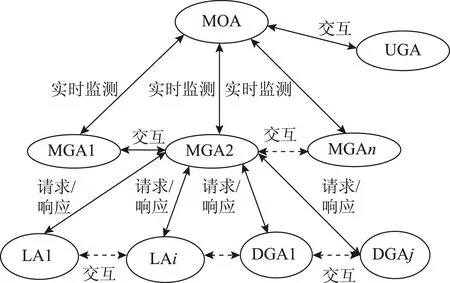
图1　三层多代理系统结构Fig.1　Implemented coordination between agents

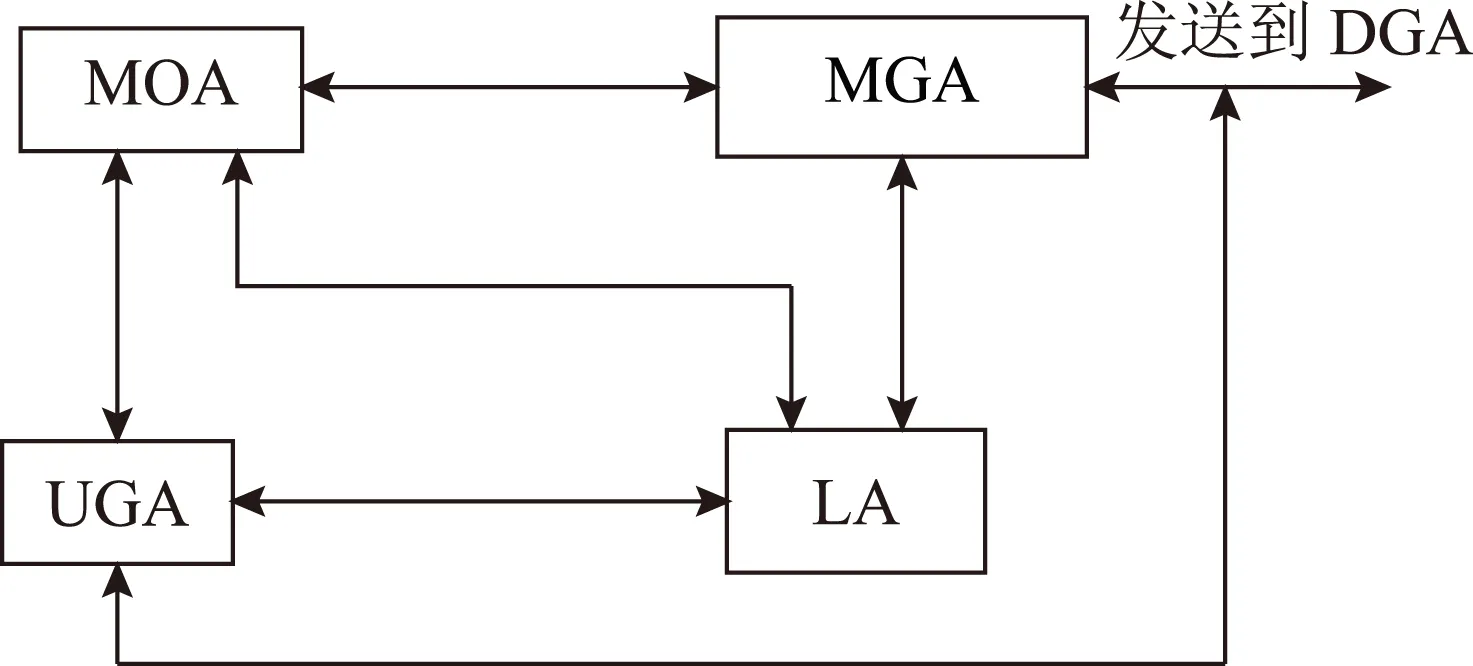
图2　电力市场竞价多代理相互协调控制策略Fig.2　Architecture of bidding information based MAS

2　电力市场竞价策略

多代理系统通过第1、2层代理相互协调来实现微电网电力市场最优竞价策略，各个参与竞标的微电网代理是由电力市场管理代理进行统一管理[17]。

假设有N个微电网参与电力市场竞价，其中一个微电网的发电成本函数为

W(PG)=a(PG)2+bPG+c

(1)

式中，PG为参与竞价微电网发出的有功功率，kW；a、b、c为参与竞价微电网的成本二次函数系数，且均是已知量；a(PG)2+bPG为可变成本，包括燃油费用、运行维护费用等；c为固定成本，包括起动费用、设备折旧费用等。

考虑到电力市场不确定性，在竞价时一般会在成本费用函数的基础上加上一定的比例因子λ， 则微电网的发电成本函数可写为

W(PG)=(1+λ)(a(PG)2+bPG+c)

(2)

微电网的利润函数即微电网的收益可写为

π=mPG-W(PG)

(3)

式中，π为微电网的竞价利润函数，USD；m为该时刻电价，USD/(kW·h)。

其他N-1个参与竞价的微电网中，第i个微电网的成本函数和利润函数可写为

W(PGi)=(1+λi)(ai(PGi)2+biPGi+ci)

(4)

πi=mPGi-W(PGi)

(5)

式中，i=1,2,…,N-1； W(PGi)为第i个参与竞价的微电网的成本函数；πi为第i个参与竞价的微电网的利润函数，USD；PGi为第i个参与竞价的微电网的输出有功功率，kW；ai、bi、ci为第i个参与竞价微电网的成本二次函数系数，是不可知量；λi为第i个参与竞价微电网的成本函数比例因子。

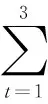
(6)

π(PGi)′=miPGi-E(W(PGi))

(7)

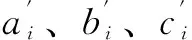
此时，该博弈模型由不完全信息模型博弈变为完全博弈模型，此模型可采用纳什均衡来求解。由平衡条件可得

(8)

(9)

根据电力市场管理中心给出该时刻需要的电量预测，确定所有微电网的总出力

(10)

式中，Pbuy为微电网向大电网购买电量，kW。

联立式(8)、式(9)和式(10)，可求得微电网最优竞价电量和微电网边际成本价格期望值

(11)

(12)

估计其他微电网的期望竞价电量和期望价格分别为

(13)

(14)

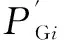
本文采用博弈理论研究微电网竞价策略。博弈论的主要元素有参与者、博弈策略、收益函数、均衡。

1)参与者是博弈中期望获得最大化的自身利益的行为主体。“两人博弈”是指博弈过程中只有2个参与者，“多人博弈”是指博弈过程中有3个或3个以上的参与者。本文中，电力市场中各个参与竞价的微电网为博弈参与者，且竞标过程属于“多人博弈”过程。

2)博弈策略是参与者博弈中执行其行为的方案，即为达到利益最大化而做出的怎样的方案选择。本文中，电力市场的竞价策略为：①负荷Agent执行预测计算，并向电力市场管理系统代理提交预测电量；②电力市场管理系统代理向各个参与竞价的微电网Agent告知电力需求量，等待同意响应；③市场运行Agent确认电力需求可行，并初始化市场；④参与竞标微电网Agent基于相关信息制定竞标策略，并向市场管理系统Agent提交竞标信息；⑤在分布式网络运行Agent确认无电网违规现象存在后，市场管理Agent计算市场清算价格和各分布式电源中标电量，并向各分布式电源Agent宣布中标结果和电价。

3)收益函数是博弈中参与者最关心的对象——利益水平，是所有参与者策略或行为的函数，如式(5)所示。

4)均衡是所有参与者达到最优结果的策略或行动的组合，一般指“纳什均衡”。

3　多时间尺度能量调度策略

由微电网电力市场最优竞价的结果可以得出日微电网最优竞价电量和电价，这些数据将被应用于多时间尺度的微电网内部能量优化分配。多代理系统通过第2、3层代理之间相互协调来执行微电网系统内部多时间尺度的能量优化管理。本文研究的多时间尺度分为日计划和实时计划。日计划为实时计划提供机组启停计划、日机组出力计划；实时计划是根据日计划所提供的数据实时的对负荷进行调整，2个时间尺度各司其职，同时兼顾上、下级时间尺度计划的协调。

3.1日计划

日计划以1 h为时间段，以24 h为周期(共计24个时间段)，依据分时电价的电费标准对负荷电量的预测值进行调整，通过建立负荷调整费用函数和约束求出负荷调整量，再以发电机组代理的成本、负荷代理购电费用、弃风惩罚、向大电网的最优竞价电量建成目标函数，求出发电机组启停状态和发电量。

本文假定电价政策为：高峰时段为8∶30～11∶30和18∶30～23∶30，低谷时段为23∶30～7∶30，其余时段为平时段；平时段执行基础电价，高峰和低谷时段分别按基础电价上下浮动。因此，分时电价可以表示为

qi=q0(1+λqi), i=1,2,…,R

(15)

式中，R为划分的时段数，本文取R=3， 将电价分为峰、平、谷3种；qi为在i时段的电价，USD/(kW·h)；q0为基础电价，USD/(kW·h)；λqi为各时间段电价相对基础电价的浮动比率。

本文发电机组有风力发电机组、燃气轮机发电机组、燃料电池发电机组3种。燃气轮机和燃料电池发电成本函数考虑发电机组的运行维护费用、燃料费用、排放污染气体折合费用，包括了经济因素和环保因素，可写为

(16)

式中，ζ1和ζ2分别为运行维护费用、燃料费用函数和排放污染气体折合费用函数的权重系数；pDG为分布式发电机组的发电量，kW；q为发电机组排放污染气体的种类；α为电机的运行和维护费用参数，USD/kW；β为燃料单价，USD/m3；χ为燃料消耗率，m3/kW；el和hl为第l种污染气体排放速率，m3/h；vl为第l种污染气体排放惩罚因子，USD/m3。

由式(16)可知，燃气轮机和燃料电池发电成本函数可写成

(17)

式中，aDG、 bDG、 cDG为分布式发电机组的成本二次函数系数，USD。

为计算方便，本文采用三分段方式进行线性化处理，如图3所示，于是分布式发电机组的边际成本为

C(PDG)1=aDGPmin+aDGe1+bDG

(18)

C(PDG)2=aDGe1+aDGe2+bDG

(19)

C(PDG)3=aDGe2+aDGPmax+bDG

(20)

式中，Pmin为发电机组的最小出力，kW；PGmax为发电机组的最大出力，kW；e1和e2为2个分段点。

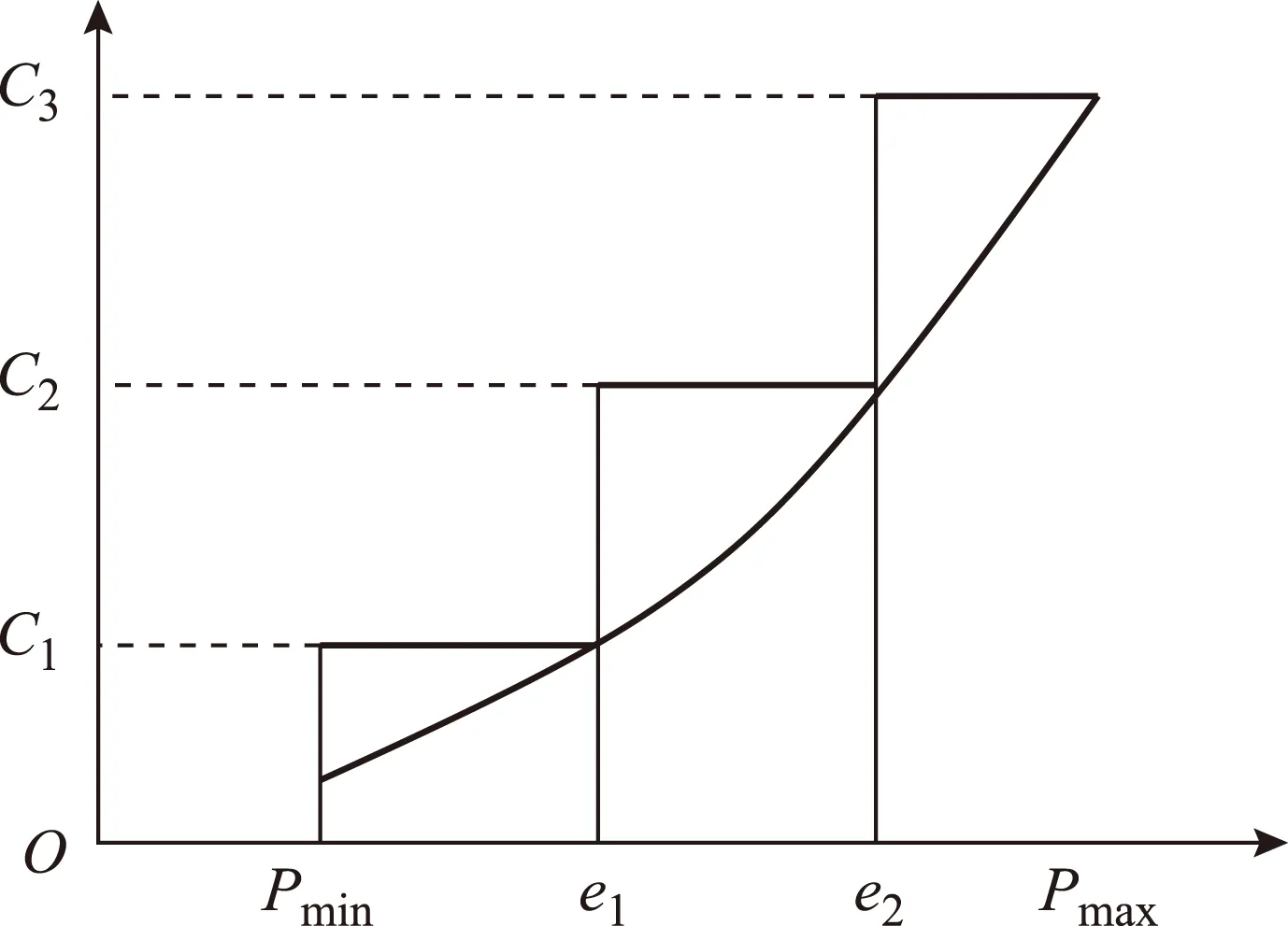
图3　发电机组的发电成本曲线Fig.3　Power generation cost curve

因此分布式发电机组根据此时段的发电机组的起动费用、无负荷费用和发电成本费用组成发电机组代理的发电成本函数为

(21)

式中，t=1,2,…,24； N为发电机组数量；Dsi,t为t时间段i机组的启停状态；FCi为i机组的无负荷费用，USD；Pi,t,k为t时间段i机组在成本曲线k段的出力；C(Pi,t,k)k是i机组在成本曲线k段的边际成本，USD；Si,t为t时间段i机组起动成本，USD。

假设在t时间段，负荷代理j检测前、后的分时电价分别为qtjB和qtjA， 检测前的负荷(预测负荷)和调整后的负荷分别为DtjB和DtjA， 则负荷的购电费用为

(22)

式中，M为负荷用户代理数量；ΔDtj为在t时间段负荷代理j的负荷调整量。

本文只考虑具有自弹性需求的电价型负荷，其功率调整特性取决于自弹系数εj、 初始功率DtjB及初始电价qtjB，所以调用电价型负荷的边际成本[19]可写为

(23)

式中，ΔDtjp为t时间段负荷代理j的调用电价型负荷的调整量。

激励性电价负荷是指实施机构通过制定确定性的或随时间变化的政策，来激励用户在系统可靠性受到影响或是电价较高或较低时及时响应消减负荷或者增加负荷。在负荷代理发出功率调整指令后，按照指令调整功率并获取相应补偿或是折扣电价。消减负荷或是增加负荷，代理调用激励型负荷的边际成本[18]可分别表示为

CtjEX=θqtjB

(24)

CtjEX=(1-δ)qtjB

(25)

式中，θ和δ分别为补偿率和折扣率。

在日计划时间段负荷代理的调整费用目标函数和约束可表示为

(26)

式中，qt为t时间段上电价，USD/(kW·h)；q0为基础电价，USD/(kW·h)；qf和qg分别为电价的峰值和谷值，USD/(kW·h)；ΔDtjpmin和ΔDtjpmax分别为调用电价型负荷代理i在t时间段上的最小调整量和最大调整量；ΔDtjEXmin和ΔDtjEXmax分别为激励型负荷代理i在t时间段上的最小调整量和最大调整量。

根据以上目标函数和约束可求解日计划内每个时间段内的满足最小负荷调整费用目标函数最小的的负荷调整量最优解。

系统总的目标函数由在t时间段的发电机组代理的成本、负荷代理购电费用、弃风惩罚、向大电网最优竞价电量构建，表达式为

(27)

功率平衡约束条件为

(28)

(29)

式中，E为风力发电机组的数量；ptlWT为t时间段风力发电机组的出力，kW。

发电机组代理的出力约束函数为

ptimin≤μi,tPi,t,k≤ptimax

(30)

式中，ptimin和ptimax分别为发电机组i在t时间段的最小出力和最大出力，kW。

3.2实时计划

实时计划以1 h为时间段，以15 min为周期(共计4个时间段)，根据实时计划依据日计划提供机组启停计划、日电量计划和机组出力调整量等数据，建立系统总的目标函数。

实时计划中在s(s=1,2,3,4)时间段，发电机组代理的发电成本函数为

(31)

在s时间段负荷代理的购电费用为

(32)

式中，Dsj为负荷代理在s时间段的购电量，kW；qtj为负荷代理在s时间段的电价，USD/(kW·h)。

实时计划中负荷代理调整费用目标函数和约束同日计划相同。

系统总的目标函数构建方法与3.1节相同，表达式为

(33)

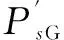
功率平衡约束条件为

(34)

式中，pslWT为s时间段风力发电机组的出力，kW。

发电机组代理的出力约束函数为

psimin≤μi,sPi,s,k≤psimax

(35)

式中，psimin和psimax分别为发电机组i在s时间段的最小出力和最大出力，kW。

3.3目标函数权重系数的确定

由于本文的微电网能量管理目标函数由发电机组代理的成本、负荷代理购电费用、弃风惩罚、向大电网的最优竞价电量构建，因此可采用二元对比法确定指标权重。首先，建立重要性排序一致性标度矩阵，设系统有待进行重要性比较的指标集D={d1,d2,…,dn}， 其中di为第i个指标，i=1,2,…,n。 将指标集中的指标作比较，例如将dm和dl作比较，若dm比dl重要，则记排序标度eml=1、elm=0； 若同样重要，则记为eml=0.5、elm=0.5。 eml、 elm只取0、0.5和1之中的某一个数。根据比较结果，建立指标集二元对比重要性定性排序标度矩阵

(36)

指标重要性排序一致性定理：若二元对比定性排序标度矩阵E满足ehk>ehl， 有elk>ekl； 满足ehkelk=0.5， 则E为排序一致性标度矩阵，其各行和数由大到小的排列顺序，给出了指标集关于重要性的排列顺序。

为使二元定量对比更符合我国的语言习惯，给出定量标度，引入语气算子和隶属度。由文献[19]提出的各种语气算子对应的隶属度，见表1。按照指标重要性排序一致性定理写出指标集二元对比重要性定性排序标度矩阵E，根据表1中语气算子与相对隶属度的对应关系，将模糊语气算子转换为各指标的相对隶属度，得到指标的非归一化权向量W′， 将其归一化，即可得到指标的归一化权向量W。

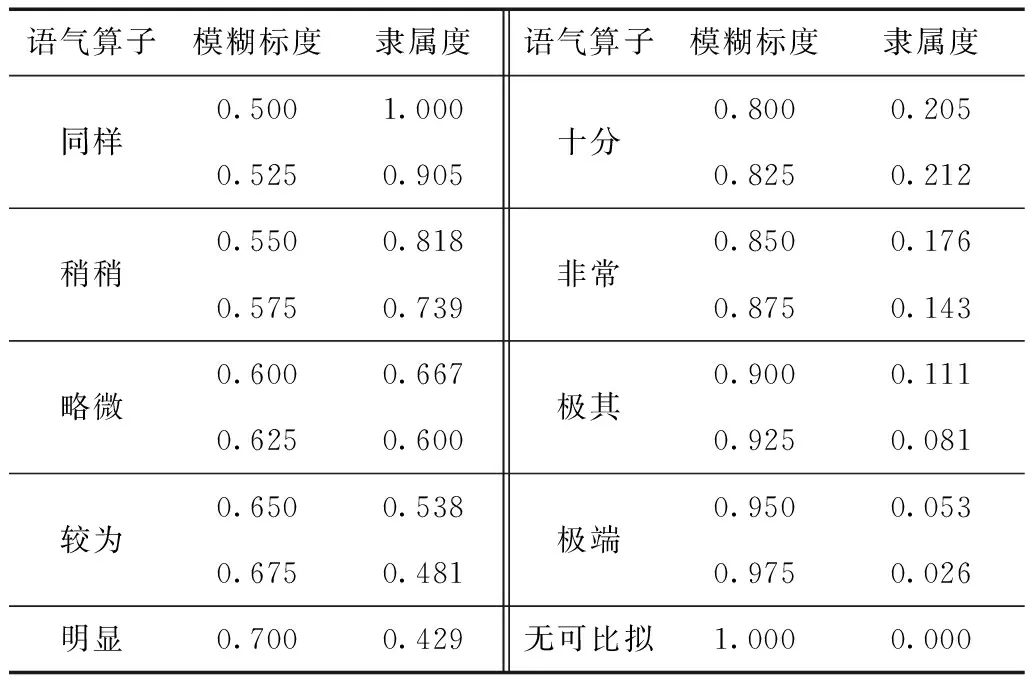
表1　语气算子与模糊标度、隶属度的对应关系Tab.1　Relationship of mood operator，fuzzy scale and membership degree

3.4日计划与实时计划的相互协调

为了满足日计划发电量的目标函数和约束，需将日计划发电量分解至各时予以具体完成。一方面，不同时间尺度的分时电价不同；另一方面，不同于日计划，实时计划不在考虑机组的启停状态和分时电价的影响。机组日计划电量分解至实时的计划电量应为一个范围，而非具体数值，由日计划得到的机组i第s时间段(15 min)的计划电量上、下限可按式(37)计算[20]。

(37)

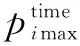
由于每隔1 h发电机组会滚动一次重新安排发电机组的启停状态和发电量计划，所以各机组计划电量的上、下限按式(38)更新。

(38)

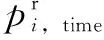
3.5具体实现流程

1)设定Tday=24。

2)判断Tday是否小于0，若是，则结束；若否，则进入步骤3)。

3)Tday=Tday-1， 求解满足日计划目标函数和约束条件的每个发电机组每小时发电量的最优解和机组的启停状态。

4)设定Ttime=4。

5)判断Ttime是否小于0，若是，则转到步骤2)；若否，则进入步骤6)。

6)Ttime=Ttime-1， 求解满足实时计划目标函数和约束条件的每个发电机组每15 min的发电量的最优解，并转到步骤5)。

3.6中心引力优化算法

在本文中，运用中心引力算法求解日计划和实时计划多目标函数的最优解。中心引力算法[21]由Formato 在2007年提出，是基于物理运动学原理构造的一种新型优化算法，通过初始化若干随机质点，每个质点有其加速度和位移，进行迭代，直至找到最优解。速度矢量和位移矢量的表达式分别为

(39)

(40)

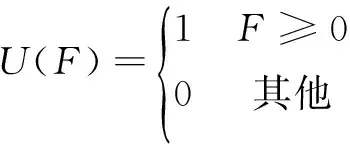
(41)

(42)

(43)

(44)

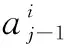
具体流程如下：

1)初始化质点群p={x1,x2,…,xNp}， 计算每个质点函数f(xi)值。

2)根据迭代比较每个质点的函数值找出最优质点函数值f(xbest)， 然后确定最优质点xbest。

3)根据式(41)～式(43)进行迭代。

4)根据目标函数更新质点函数值。

5)如果达到完成迭代条件后，则终止跳出循环，如果没有达到则跳转到步骤3。

3.7混沌理论预测算法

日微电网负荷预测和风力发电预测为微电网多时间尺度能量调度策略提供数据。本文运用混沌理论算法[22]对日负荷预测和风电发电量进行预测。

1)重构相空间。

重构相空间理论是由Packard 和Takens等提出的，将混沌理论引入到时间序列分析。混沌预测是建立在序列的重构相空间基础之上。定义一组时间序列{x(i)},i=1,2，…，N， 嵌入维数和延迟时间分别为m和τ。 向空间重构为

X(i)=[x(i),x(i+τ),…,x(i+(m-1)τ)]

(45)

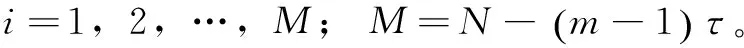
在相空间重构中，延迟时间τ和嵌入维数m为最重要的两个参数。τ和m并非各自独立的两个量，嵌入窗宽揭示了二者间的相关性

τW=(M-1)τ

(46)

式中，τW为嵌入窗宽。

在本文中，把时间序列{x(i)},i=1,2，…，N分解成长度为INT(N/t)的t个不相交的时间序列，INT为取整函数，t为一般的自然数。分解过程为

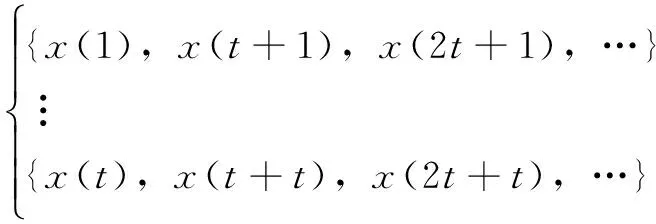
(47)

计算每个子序列的统计量s(m,N,r,τ)：

s(m,N,r,τ)

(48)

式中，cl为第l个子序列的关联积分，定义为

c(m,N,r,τ)

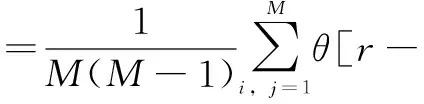
(49)

式中，θ(·)为Heaviside单位函数；X(i)和X(j)分别为第i个和第j个时间序列。

局部最大间隔可取s(·)的零点或对所有半径r相互差别最小的时间点。选择对应值最大和最小两个半径r， 定义差量为

ΔS(m,N,T)

=max[S(m,N,ri,τ)]-min[S(m,N,rj,τ)]i≠j

(50)

根据统计学的原理，r的取值在σ/2和2σ之间，m取值为2～5，σ为时间序列的均方差，得到以下方程[23]

(51)

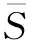
2)李雅普诺夫指数预测方法。

李雅普诺夫指数指出了系数误差在相空间中沿特征向量方向的指数增长率，它为估计系统初始轨道的指数发散和混沌行为的量化指标。李雅普诺夫指数的估计值为

(52)

式中，k为迭代次数；Lk-1为两个初始点的距离；Lk为经过k次迭代后两个点之间的距离。

假设参考点为X(ti)， 与参考点最近邻态为Xnbt(ti)，Xnbt(ti)可定义为

Xnbt(ti)=min[‖Xi-Xi+j‖]j=1,2,…,(M-1)

(53)

假设经过k次迭代后参考点X(ti)变为Xi+k， 如果k<τ， 则Xi+k只有一个分量是未知的、M-1个分量是已知的。一维李雅普诺夫指数预测模型为

(54)

最大李雅普诺夫指数预测算法流程如下：

①初始化时间序列，确定样本空间N。

②同步计算嵌入维数m和延迟时间τ。

③计算李雅普诺夫指数λ， 若λ<0， 转到步骤⑨；若λ≥0则进行步骤④。

④根据嵌入维数和延迟时间重构相空间。

⑤最后已知点X(N-(m-1)τ)并计算最近邻态X(Min)。

⑥计算X(Min)和X(N-(m-1)τ)的直线距离。

⑦计算X(Min+1)和X(N-(m-1)τ)的直线距离。

⑧计算X(Min+1)在重构相空间的坐标，根据λ预测X(N+1)的时间域值。

⑨若满足终止条件，则结束程序输出结果；否则，转到步骤②。

4　算例分析

4.1微电网电力市场竞价仿真

本文假设参与电力市场竞价的微电网有3个，将微电网1作为参考对象，微电网2、3是竞价对手，3个微电网的成本比例为固定值0.2，即1+λ在0.8、1、1.2中取值，比例因子的概率分布可见表2。3个微电网的竞价参数以及微电网2、3的竞价参数概率分布见表3，其中表2和表3的一些数据是由文献[24]获得的。

表2　微电网2和3中比例因子的概率分布Tab.2　Probability distribution of λ about MG 2 and 3

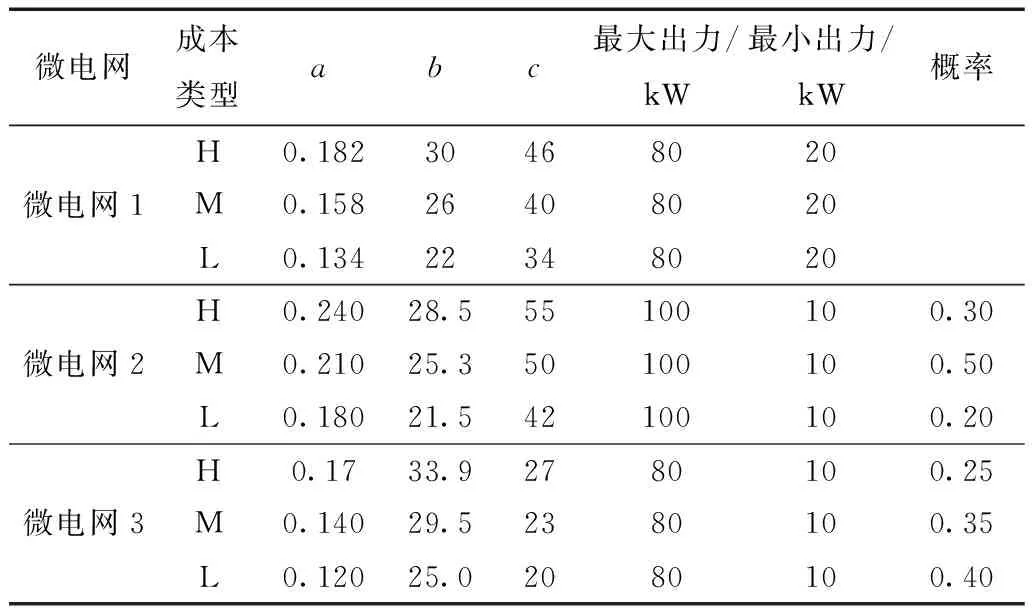
表3　微电网竞价参数Tab.3　The cost parameter of MG

表3中H、M、L分别代表微电网的高、中、低成本战略。因为参考微电网1比例因子在0.8、1、1.2中取值，成本竞价参数根据高、中、低成本战略有3种取值，所以参考电网的成本函数有9种选择。为方便研究，参考微电网1的比例因子为1，竞价参数选取中成本战略的。

图4为电力市场在日内每小时所需电量图，可见在3∶00时需求量最低，在21∶00时需求量最高。数据通过大电网传送到电力市场管理代理，根据本文所研究的电力市场竞价策略，可以分别求得微电网1、2、3的最优竞价电量，如图5所示。由图5可见：微电网3基本保持在最大输出功率值；微电网1在2∶00～8∶00基本保持在最小输出功率值；微电网2在1∶00～9∶00基本保持在最小输出功率值。根据图5所得的最优解，可以求得微电网1、2、3的最大利润值，如图6所示。

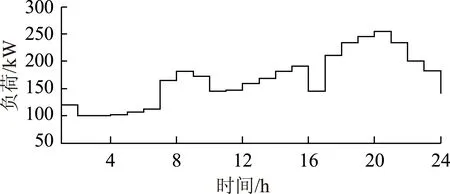
图4　日电力市场需求量Fig.4　Daily demand of MOA

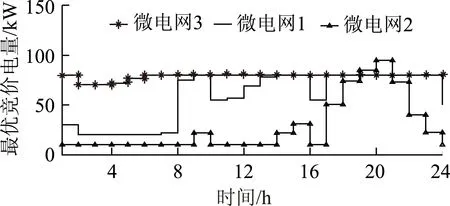
图5　日微电网最优竞价电量Fig.5　Daily optimal bidding energy profits of MG1，MG2 and MG3

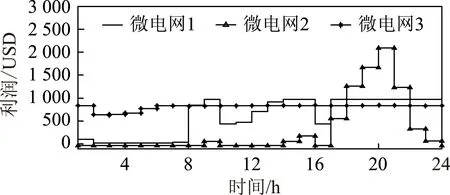
图6　日微电网利润Fig.6　Daily profits of MG1，MG2 and MG3

4.2微电网多时间尺度仿真与分析

1)日计划负荷和风电发电量的预测。

本文选取一个月30天的数据作为样本数据进行提取李雅普诺夫指数计算，可得出日负荷预测值和风力发电机组日发电量值，如图7和图8所示。

图7　日负荷预测值和实际值Fig.7　Daily forecast load value and actual load value

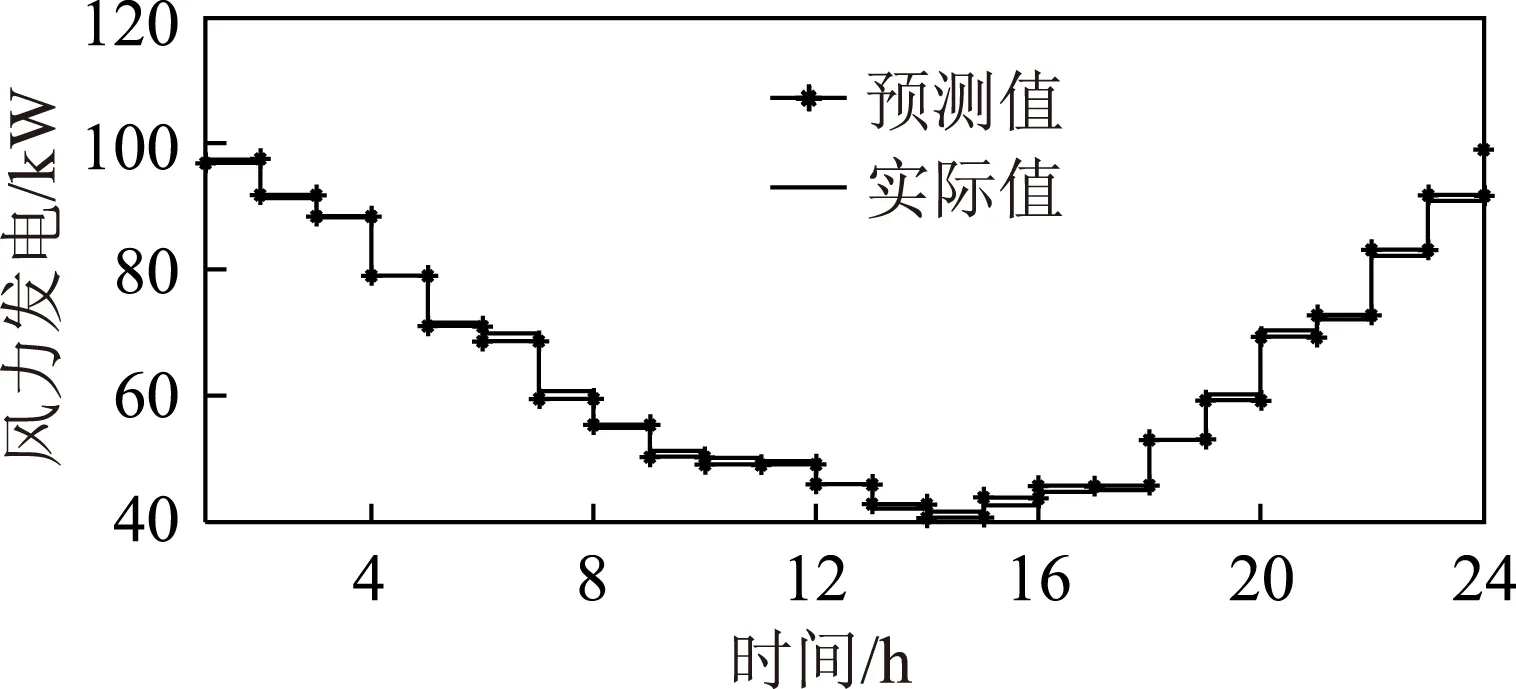
图8　日风力发电机组发电预测值和实际值Fig.8　Daily forecast load value and actual of WT outpower

2)日计划负荷调整。

根据负荷调整费用目标函数和约束可求得日内计划每个时间段的负荷调整量，如图9所示。

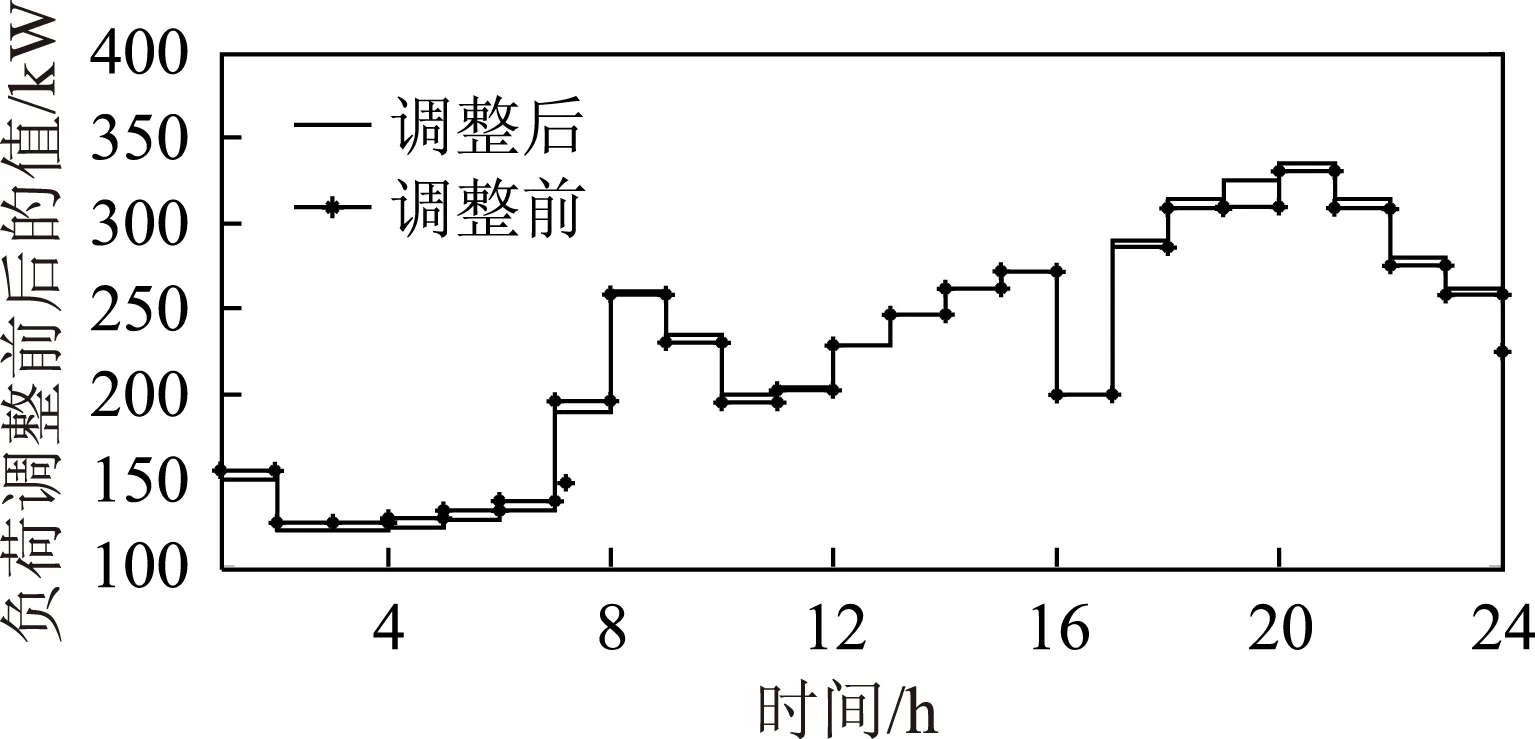
图9　日负荷调整前后值Fig.9　Daily load value and after adjusting the value of the load

3)日计划发电机组能量优化。

燃气轮机发电机组和燃料电池发电机组的数据见表4～表6。

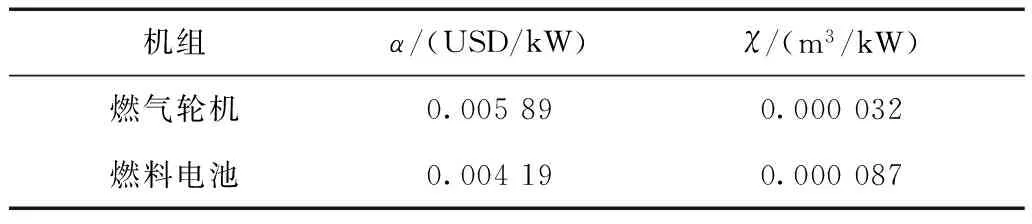
表4　微型燃气轮机和燃料电池机组参数Tab.4　Parameters of micro gas turbine and fuel cell

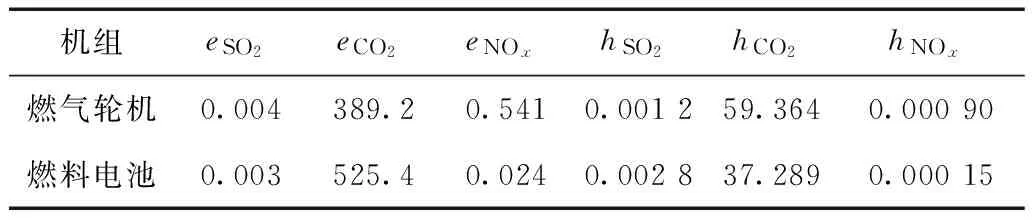
表5　微型燃气轮机和燃料电池机组排放参数Tab.5　Parameters of pollution gas

表6　微型燃气轮机和燃料电池机组数据Tab.6　Parameters of micro gas turbine and fuel cell

根据实时计划的目标函数和约束可以求得日内每小时燃气轮机发电机组和燃料电池发电机组的启停状态和发电量。表7为每小时燃气轮机发电机组和燃料电池发电机组的起动发电机数量。图10为每小时燃气轮机发电机组和燃料电池发电机组的发电量。

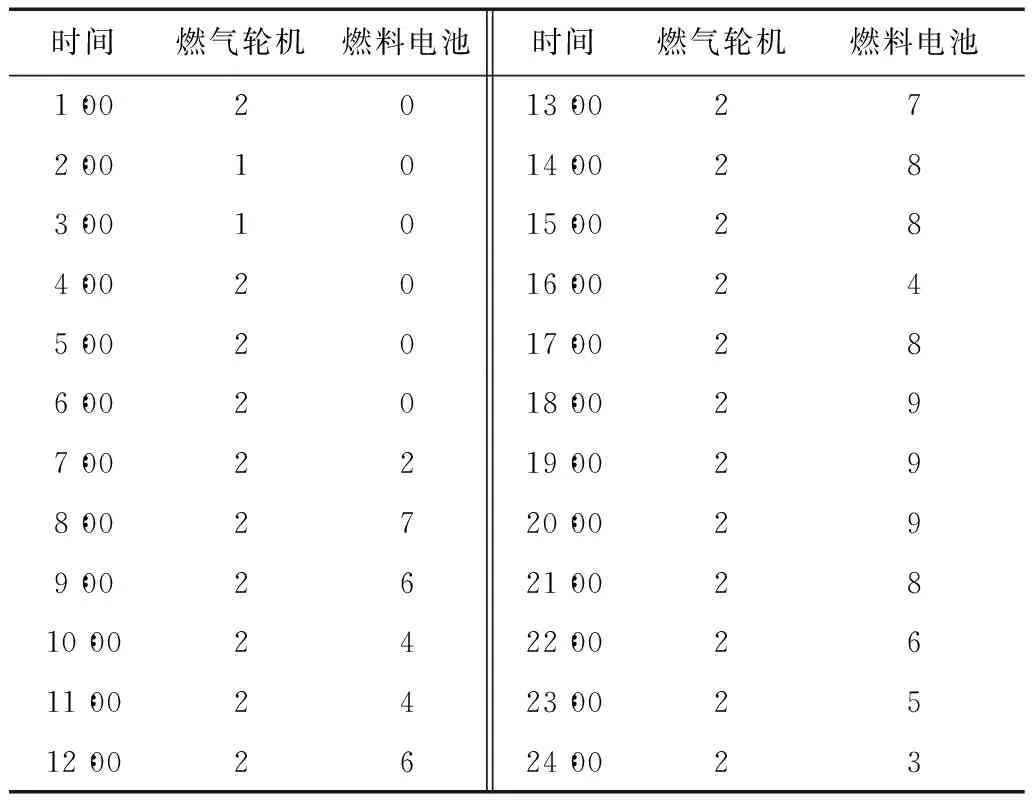
表7　微型燃气轮机和燃料电池起动数量Tab.7　Running numbers of micro gas turbine and fuel cell

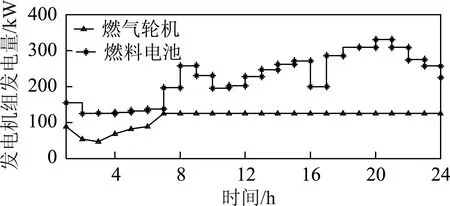
图10　燃气轮机发电机组和燃料电池发电机组的发电量Fig.10　Daily output power of FC and MT

图11为日目标函数值，是根据本文日目标函数求解的。另外，不考虑需求侧响应即不对负荷进行调整的目标函数值也被求解出，与考虑需求侧响应的目标函数值进行对比。从图中可看出在本文假定电价政策高峰时段调整负荷的目标函数值小于不调整负荷的目标函数值；在低谷时间段调整负荷的目标函数值大于不调整负荷的目标函数值。可以计算日目标函数总值调整和不调整负荷的目标函数值总值分别为5 842.150 0和5 876.328 4。由此可知调整后整体目标函数减小，即负荷代理购电费用减小，更加经济。

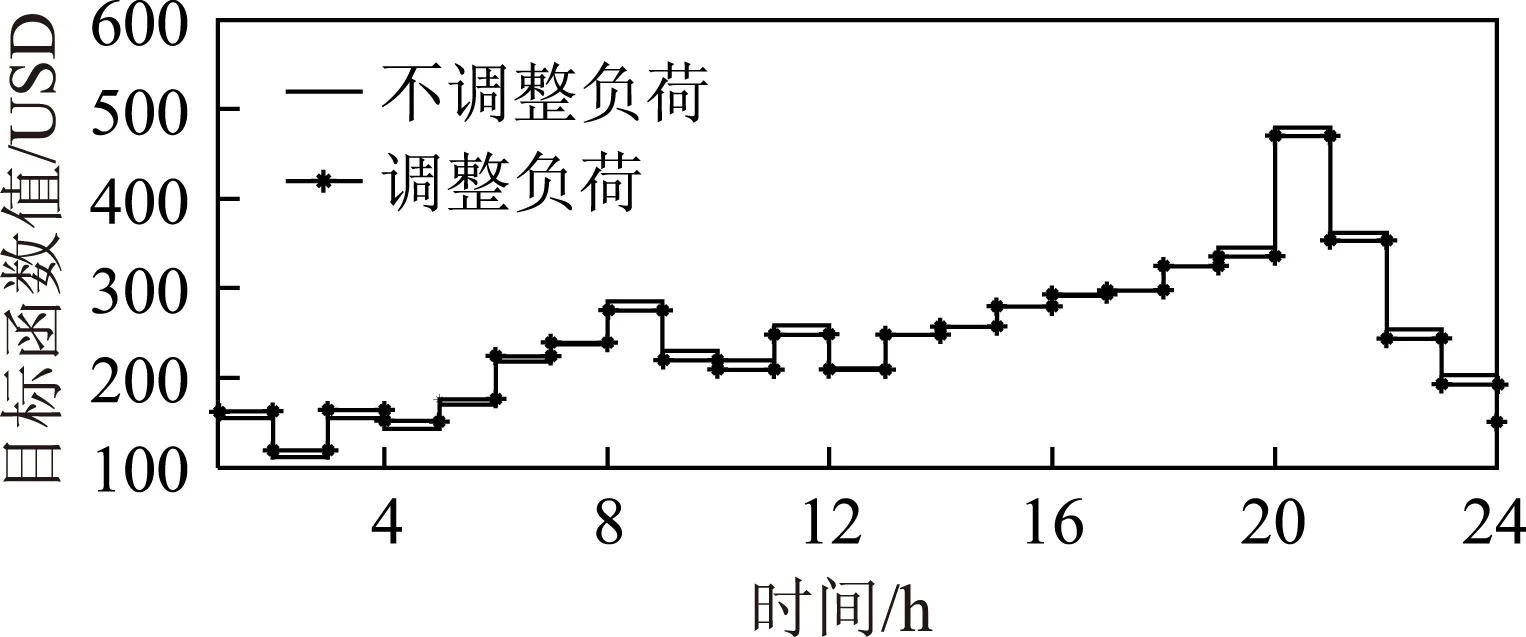
图11　日目标函数值Fig.11　Daily objective function value

4)实时计划仿真。

机组日计划电量分解至实时的计划电量为一个范围，而非具体数值。根据式(36)、式(37)可以求得每15 min发电机组发电量的上下限值。本文选取日计划23∶00为参考时间段进行实时计划仿真。由日计划仿真可知在23∶00时，燃气轮机和燃料电池起动数量分别为2和5；由分时电价可知23∶00～23∶30是高峰电价23∶30～24∶00是低谷电价，所以负荷需要调整，在23∶00～23∶30时负荷需要减少，在23∶30～24∶00时负荷需要增加。由负荷调整费用目标函数和约束可求得负荷调整量在23∶00时分别为-4.036、-3.963、4.010、4.010。实时计划目标函数用中心引力算法优化仿真可求得在23∶00时燃气轮机发电机机组和燃料电池发电机组的发电量见表8。

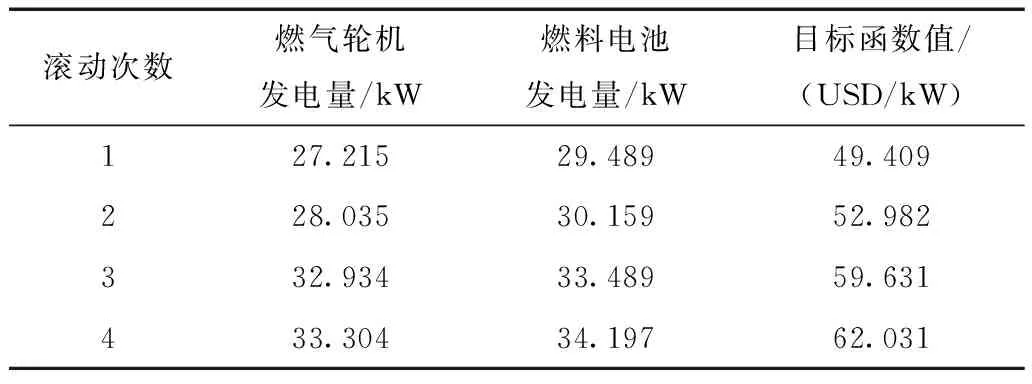
表8　23∶00时燃气轮机和燃料电池发电机组的 发电量和目标函数值Tab.8　Objective function value and output powers of MT and FC at 23∶00

5　结论

本文建立了三层多代理系统对微电网进行协调能量管理，其中上层代理和中层代理相互协调控制是执行基于博弈论的微电网电力市场竞价策略，中层代理和下层代理相互协调控制是执行考虑需求侧微电网的多时间尺度调度策略。算例分析中，首先根据微电网电力市场竞价策略，得出参与竞价的微电网的最优竞价电量和利润；然后，将所得结果用到参考电网多时间尺度的仿真中。多时间尺度调度策略分为日内计划和实时计划，日内计划首先运用基于混沌理论李雅普诺夫指数预测算法预测负荷和风力发电，为优化提供数据。随后，用中心引力最优算法求出日计划发电机组的启停状态、发电机组的发电量、目标函数值，并且将目标函数值与不考虑需求侧响应的目标函数值对比，得出本文考虑需求侧响应的日计划更加经济。最后，将日计划求解的发电机组的启停状态、发电机组的发电量的数据提供给实时计划，选取23∶00时对实时计划的目标函数求解，得出最优解。由仿真结果可知，本文研究的微电网多尺度能量管理策略确保了微电网供用电的经济性。

[1]王成山，武震，李鹏.微电网关键技术研究[J].电工技术学报，2014，29(2)：1-12.

Wang Chengshan，Wu Zhen，Li Peng.Research on key technologies of microgrid[J].Transactions of China Electrotechnical Society，2014，29(2)：1-12.

[2]张建华，于雷，刘念，等.含风/光/柴/蓄及海水淡化负荷的微电网容量优化配置[J].电工技术学报，2014，29(2)：102-112.

Zhang Jianhua，Yu Lei，Liu Nian，et al.Capacity configuration optimization for island microgrid with wind/photovoltaic/diesel/storage and seawater desalination load[J].Transactions of China Electrotechnical Society，2014，29(2)：102-112.

[3]郭思琪，袁越，张新松，等.多时间尺度协调控制的独立微网能量管理策略[J].电工技术学报，2014，29(2)：122-129.

Guo Siqi，Yuan Yue，Zhang Xinsong，et al.Energy management strategy of isolated microgrid based on multi-time scale coordinated control[J].Transactions of China Electrotechnical Society，2014，29(2)：122-129.

[4]李东东，崔龙龙，林顺富，等.家庭智能用电系统研究及智能控制器开发[J].电力系统保护与控制，2013，41(4)：123-129.

Li Dongdong，Cui Longlong，Lin Shunfu，et al.Study of smart power utilization system and development of smart controller for homes[J].Power System Protection and Control，2013，41(4)：123-129.

[5]Logenthiran T，Srinivasan D，Khambadkone A M.Multi-agent system for energy resource scheduling of integrated microgrids in a distributed system[J].Electric Power Systems Research，2011，81(1)：138-148.

[6]丁明，马凯，毕锐.基于多代理系统的多微网能量协调控制[J].电力系统保护与控制，2013，41(24)：1-8.

Ding Ming，Ma Kai，Bi Rui.Energy coordination control of multi-microgrid based on multi-agent system[J].Power System Protection and Control，2013，41(24)：1-8.

[7]杨丽君，于琦，魏玲玲，等.基于移动多代理动态联盟的配电网故障恢复研究[J].电工技术学报，2016，31(8)：147-155.

Yang Lijun，Yu Qi，Wei Lingling，et al.A distribution network fault recovery study on the dynamic alliance of mobile multi-agent[J].Transactions of China Electrotechnical Society，2016，31(8)：147-155.

[8]艾芊，章健.基于多代理系统的微电网竞价优化策略[J].电网技术，2010，34(2)：46-51.

Ai Qian，Zhang Jian.Optimization bidding strategies of microgrids based on multi-agent system[J].Power System Technology，2010，34(2)：46-51.

[9]Wang Jianhui，Zhou Zhi，Botterud A.An evolutionary game approach to analyzing bidding strategies in electricity markets with elastic demand[J].Energy，2011，36(5)：3459-3467.

[10]Langary D，Sadati N，Ranjbar A M.Direct approach in computing robust Nash strategies for generating companies in electricity markets[J].Electrical Power and Energy Systems，2014，54(54)：442-453.

[11]Kazemi M，Ivatloo B M，Ehsan M.Risk-based bidding of large electric utilities using information gap decision theory considering demand response[J].Electric Power Systems Research，2014，114(3)：86-92.

[12]Nojavan S，Zare K，Ashpazi M A.A hybrid approach based on IGDT-MPSO method for optimal bidding strategy of price-taker generation station in day-ahead electricity market[J].Electrical Power and Energy Systems，2015，69：335-343.

[13]陈昌松，段善旭，蔡涛，等.基于改进遗传算法的微网能量管理模型[J].电工技术学报，2013，28(4)：196-201.

Chen Changsong，Duan Shanxu，Cai Tao，et al..Microgrid energy management model based on improved genetic arithmetic[J].Transactions of China Electrotechnical Society，2013，28(4)：196-201.

[14]麻秀范，崔换君.改进遗传算法在含分布式电源的配电网规划中的应用[J].电工技术学报，2011，26(3)：175-181.

Ma Xiufan，Cui Huanjun.An improved genetic algorithm for distribution network planning with distributed generation[J].Transactions of China Electrotechnical Society，2011，26(3)：175-181.

[15]Zakariazadeh A，Jadid S.Smart microgrid energy and reserve scheduling with demand response using stochastic optimization[J].Electrical Power and Energy Systems，2014，63(12)：523-533.

[16]Mazidi M，Zakariazadeh A，Jadid S，et al.Integrated scheduling of renewable generation and demand response programs in a microgrid[J].Energy Conversion and Management，2014，86(10)：1118-1127.

[17]Handschin E，Slomski H.Unit commitment in thermal power systems with long-term energy constraints[J].IEEE Transactions on Power Systems，1990，5(4)：1470-1477.

[18]杨胜春，刘建涛，姚建国，等.多时间尺度协调的柔性负荷互动响应调度模型与策略[J].中国电机工程学报，2014，34(22)：3664-3673.

Yang Shengchun，Liu Jiantao，Yao Jianguo，et al.Model and strategy for multi-time scale coordinated flexible load interactive scheduling[J].Proceedings of the CSEE，2014，34(22)：3664-3673.

[19]曹永强，王本德，刘金禄.基于二元对比定权法的水质评价模型及其应用[J].水电能源科学，2002，20(3)：19-21.

Cao Yongqiang，Wang Bende，Liu Jinlu.Water quality assessment model based on dualistic factor contrast for indexes weight calculation and its application[J].International Journal Hydroelectric Energy，2002，20(3)：19-21.

[20]栗然，崔天宝，肖进永.基于云模型的短期电价预测[J].电网技术，2009，33(17)：185-190.

Li Ran，Cui Tianbao，Xiao Jinyong.Short term electricity price forecasting based on cloud model[J].Power System Technology，2009，33(17)：185-190.

[21]Green R C，Wang Lingfeng，Alam M.Training neural networks using central force optimization and particle swarm optimization：insights and comparisons[J].Expert Systems with Applications，2012，39(1)：555-563.

[22]Kouhi S，Keynia F，Ravadanegh S N.A new short-term load forecast method based on neuro-evolutionary algorithm and chaotic feature selection[J].Electrical Power and Energy Systems，2014，62(11)：862-867.

[23]韩敏.混沌时间序列预测理论与方法[M].北京：中国水利水电出版社，2007.

[24]陈鹏，周晖.微电网电力市场交易模型[J].电力需求侧管理，2011，13(4)：23-29.

Chen Peng，Zhou Hui.Research on trading model of micro-grid under market conditions[J].Power DSM，2011，13(4)：23-29.

Multiple-Time-Scales Optimal Energy Management in Microgrid System Based on Multi-Agent-System

Jia Xingbei1Dou Chunxia1Yue Dong2Xu Shiyun3

(1.Institute of Electrical EngineeringYanshan UniversityQinhuangdao066004China 2.Institute of Advanced TechnologyNanjing University of Posts and Telecommunications Nanjing210023China 3.China Electric Power Research InstituteBeijing100192China)

The microgrid (MG) energy management strategy based on multi-agent-system (MAS) is researched in this paper.Firstly，a three-level multi-agent-system is constructed.Then，the optimal power market bidding strategies are researched between the upper-level and middle-level agents considering the MG profit maximization.Thirdly，taking a microgrid as the research object and considering demand response (DR)，multi-time-scales energy management strategies are produced for distributed energy resources.Finally，taking into aocount the short-term load farecasting and renewable energy generations forecasting are guarantee for scheduling strategy,so, in the short-term load and renewable energy generation are forecasted by chaos phase space theory.The simulation results verify the effectiveness of the proposed energy management approach.

Multi-agent-system，microgrid，multi-time-scales，energy management，power market，bidding strategy

2015-06-04改稿日期2015-09-25

TM73

贾星蓓女，1986年生，博士研究生，研究方向为微电网能量优化管理策略。

E-mail：jiaxingbei1986@163.com

窦春霞女，1967年生，教授，博士生导师，研究方向为新能源控制技术、电力大系统分布式控制、微电网智能控制等。

E-mail：cxdou@ysu.edu.cn(通信作者)

国家自然科学基金项目资助(51177142,61573300)。