基于双层阻抗模型的三相单芯电缆自恢复故障定位

张　姝　林　圣　唐　进　何正友

(西南交通大学电气工程学院　成都　610031)



基于双层阻抗模型的三相单芯电缆自恢复故障定位

张姝林圣唐进何正友

(西南交通大学电气工程学院成都610031)

地下电缆的失效过程伴随着周期性发生的自恢复故障。快速准确地定位这类故障能够在电缆发生永久性击穿之前发现电缆潜在故障位置，为电缆的运维检修提供依据。计及电缆金属护层的影响，提出一种基于双层阻抗模型的三相单芯电缆自恢复故障定位方法。推导了双层阻抗模型下，三相单芯电缆导芯-护套自恢复接地故障和导芯-护套自恢复短路故障下的故障回路方程。利用电缆首端监测的电流电压波形，在较短故障时间下得到故障位置信息，最后通过最小二乘回归法实现了三相单芯电缆自恢复故障定位。大量仿真表明，计及电缆护套行为的故障定位算法能够准确识别电缆自恢复故障位置。该算法相对于只考虑导芯阻抗的算法更符合电缆实际模型，能够反映三相单芯金属护层的电气行为。

单芯电缆金属护套自恢复故障双层阻抗故障定位

0　引言

地下电缆具有供电可靠性高、受环境影响小及敷设美观等优点，逐步在配电网中，特别是在铁路、煤矿等特殊配电系统中广泛应用[1]。但是，由于电力电缆敷设在地下，故障后无法直观被发现，因此地下电缆的故障定位对电缆线路的运行维护具有重要的现实意义[2，3]。

地下电缆故障可以分为早期故障和永久性故障两类[4]。相对于架空线，电缆失效是长时间逐渐变化的过程。电缆故障早期表现为间歇性的自恢复故障。这类故障通常出现在线路电压的波峰或者波谷处，故障持续时间较短，一般不超过2个周波，之后线路恢复正常。这种间隙性自恢复故障是由于电缆存在水树等绝缘状况恶化产生的电弧放电[5]。随着电缆故障的发展，导致这类间歇性故障更加频繁的发生，直至最后绝缘被击穿成为永久性故障。因此，如果能够准确地定位电缆出现的这类短时的自恢复故障，在预防性检修时给予及时的维护，将避免电缆永久性故障导致的失电损失。

目前，针对电缆的非破坏性故障定位最主要的方法有行波法和故障分析法。文献[6-9]利用故障产生的暂态行波波头的时间差进行故障定位。该方法对波头识别要求高，受到故障角度的影响大，在配电网中的实用性还待进一步研究。另外一种利用高压信号促使电缆电弧放电的行波测距法[10-12]在电缆检测装置中广泛应用。此类方法需要外加高压设备且只能离线检测一般仅在电缆永久故障后的检修中使用。故障分析法是依据单端或双端采集的电气量对线路故障方程进行求解，能够实现在线的电缆故障定位[13，14]。电缆的间歇性自恢复故障，由于其故障持续时间较短，基于电气相量分析的故障分析法[15]需要大量的时间计算故障后的稳态相量，不适用于此类故障。另外基于知识的智能算法[16]也逐步引入地下电缆配电网检测定位中，该类方法需要大量的样本训练，建立故障样本库，用于在线的电缆故障定位有还一定难度。

本文针对电缆多层结构的特点，考虑了金属护层对导芯的电气影响[17]，建立了电缆的双层阻抗模型。在此基础上，针对电缆绝缘恶化发生的间歇性自恢复故障，利用基于电气量时域分析的故障分析方法分别建立了导芯-护套接地故障和导芯-护套短路故障方程。由于只需要电气量的采样值，能够在较少的信息量下得到故障信息，最后通过最小二乘回归法实现了三相单芯电缆自恢复故障定位。大量仿真实验验证了该方法能够快速、准确地识别电缆的潜在故障位置，为电缆运维检修提供了依据。

1　单芯电缆双层阻抗等效模型

单芯电缆在电网中广泛应用。例如高速铁路10 kV电力贯通线采用的即是三相单芯的电缆供电。单芯电缆的典型结构如图1所示。

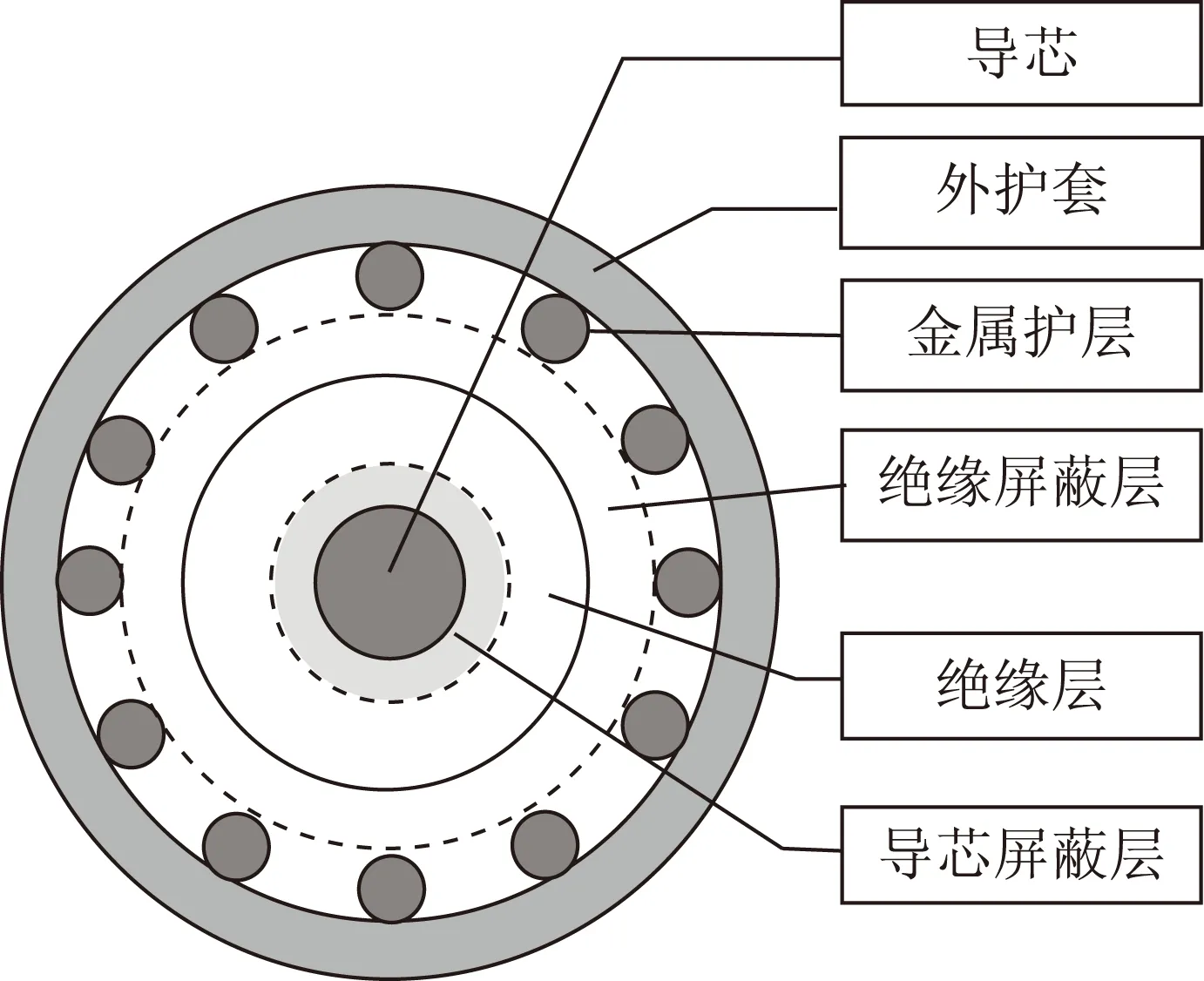
图1　典型单芯电缆结构图Fig.1　The structure of the single core cable

大多数电缆定位研究将单芯电缆等效为单导体模型，即仅考虑了导芯的电气特性。但实际上，电缆的金属护层也具有电气特性。因此，本文考虑了单芯电缆的金属护层结构的特点，建立电缆双层阻抗模型如图2所示。

图2　三相单芯电缆双层阻抗模型Fig.2　The double impedance model of three-phase single-core cables

由图2可知，三相单芯电缆等效为6根导体的集中参数模型[15]。本文考虑了单芯电缆护层的导体阻抗影响，为简化模型计算，忽略了对地电容的影响[18,19]。图2中仅以A相与其他两相的耦合关系为例，A相导芯与A相金属护层、B相导芯、B相金属护层、C相导芯、C相金属护层之间，A相金属护层与B相导芯、B相金属护层、C相导芯、C相金属护层之间均存在电气耦合关系。对于图2中的双阻抗模型，三相单芯电缆的阻抗矩阵如式(1)所示。

(1)

所建的单芯电缆双层阻抗模型，其单位阻抗为6×6的矩阵，含6根导体的自阻抗和互阻抗。式中，ZAA、Zaa、ZBB、Zbb、ZCC、Zcc为三相导芯和三相互层阻抗；ZAa、ZBb、ZCc为三相导芯与同相护层的互阻抗；ZAB、ZAC、ZBC、Zab、Zac、Zbc为三相导芯之间，金属护层之间的互阻抗。

2　自恢复故障分析

2.1电缆自恢复故障建模

自恢复性故障的特点是持续时间较短，通常在1/4周波至两个周波之间，与间歇性的弧光接地故障特征相似，配电网常见的过电流保护装置不能识别此类故障。文献[19，20]中通过变电站电能质量在线监测装置记录到的地下电缆配电系统发生的自恢复故障电压和电流波形如图3所示。

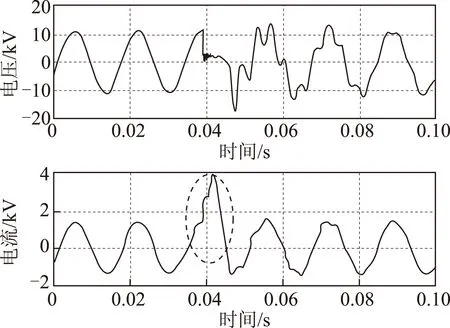
图3　实际线路监测的自恢复故障电压和电流波形Fig.3　The actual monitoring voltage and current waveforms of the self-clearing fault

通过线路上安装的电能质量监测设备记录的波形特征，可以发现自恢复故障通常发生在电压峰值处，持续时间在1/4周波到两个周波左右，故障期间故障电压接近恒定值，在接近永久性故障时自恢复故障发生的间隔会越来越短[20]。电缆的自恢复故障是由于电缆的绝缘退化导致的间歇性击穿放电，与间歇性电弧故障特征相似。Mayr电弧故障模型对描述电流零区的电弧伏安特性精确度较高，所含故障信息丰富，在电力系统中被广泛使用[21，22]。因此，本文采用Mayr型模拟电缆自恢复故障特征。

电弧电导的微分方程为

(2)

式中，τ为电弧的时间常数；g为瞬时电弧电导；G为固定电弧电导，其定义为

(3)

(4)

式中，iarc为瞬时电弧电流；ust为静态电弧电压;u0为电弧电压特征;r0为电弧电阻。电弧时间常数为

(5)

式中，τ0为初始时间常数；l0为电弧初始长度；α为负值系数。电弧伸展率为

(6)

式中，vth为初始暂态的电压瞬时值；vmax为正常条件下电压幅值最大值。以Mayr电弧模拟的1/4周期间歇性自恢复故障下故障点处的电流电压波形如图4所示。由图4可见，该模型下的故障电压近似为常数，电流在1/4周期内发生突变，与通过电能质量监测设备监测得到的自恢复故障特征一致，因此，用Mayr电弧故障模型能够较好地模拟电缆自恢复故障特性。

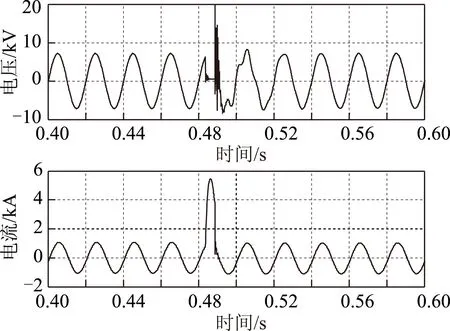
图4　四分之一周期自恢复故障模拟波形Fig.4　The simulation waveform of self-clearing fault with 1/4 cycle

2.2导芯-护层接地故障

对于单芯电缆接地故障，通常是由于电缆绝缘层放电击穿导致导芯、金属护层、外护套等贯穿性接地故障。本文考虑电缆故障时金属护层的电气影响，将电缆等效为双层阻抗模型。在电缆发生导芯-护层接地故障时，其电路原理分析如图5所示，当A相发生导芯-护层接地故障，利用KVL建立方程，这里考虑各个导体之间的互阻抗作用的影响，如式(7)所示。

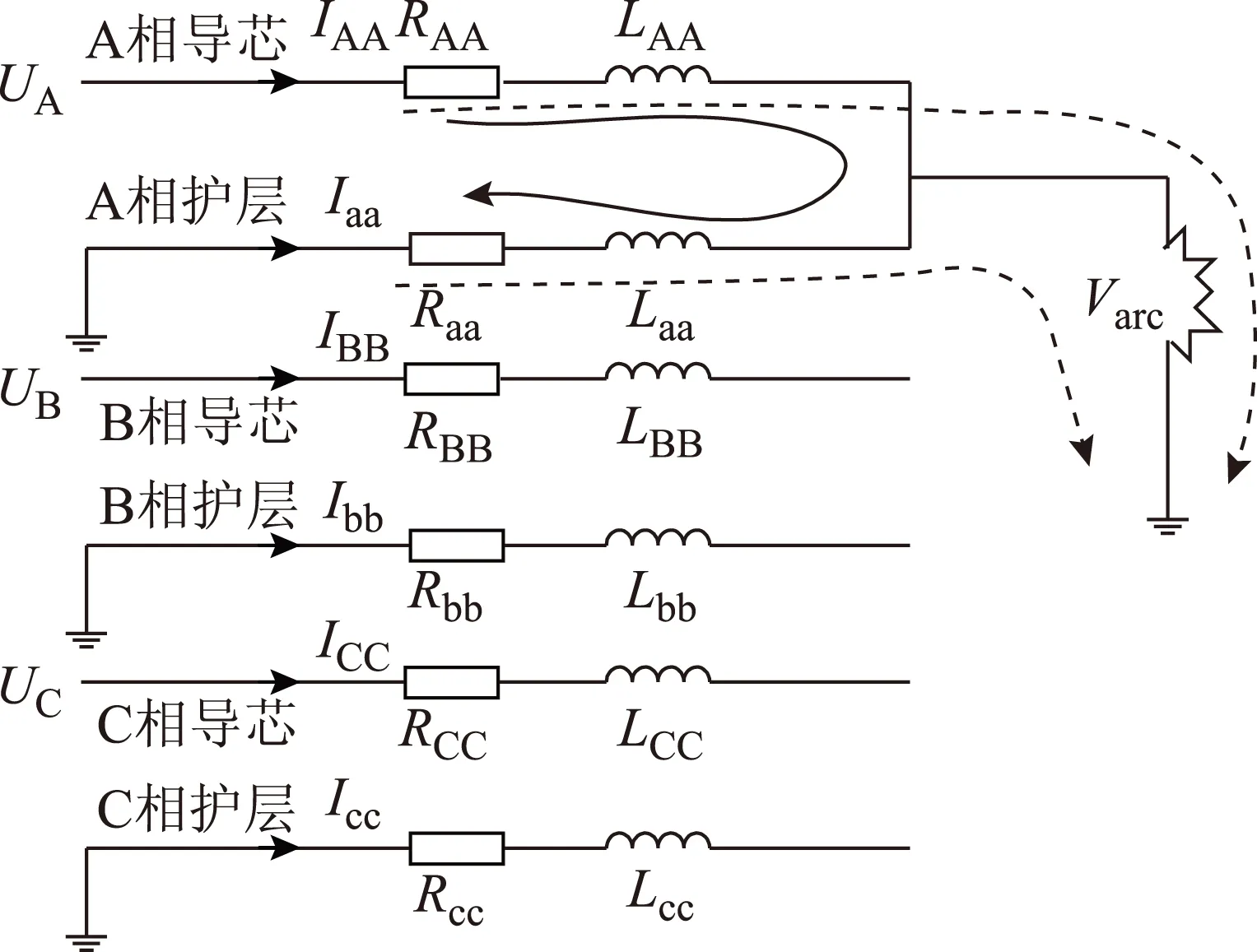
图5　A相导芯-护层接地短路自恢复故障电路分析Fig.5　The circuit of the core-sheath-ground self-clearing fault in the A phase

(7)

式中，UMA为A相导芯以外的其他导体由于互阻抗作用在A相导芯上产生的压降；UMa为A相护层以外的其他导体由于互阻抗作用在A相护层上产生的压降。

(8)

(9)

式中，IAA、Iaa、IBB、Ibb、ICC、Icc分别为A、B、C相导芯电流和其护层上的电流；RAa、LAa、RAB、LAB、RAb、LAb、RAC、LAC，RAc、LAc分别为A相导芯与其他导体之间的互阻和互感；RaB、LaB、Rab、Lab、RaC、LaC、Rac、Lac分别为A相护层与其他导体之间的互阻和互感。由于三相单芯电缆结构一致，因此，参数满足

RAB=RaBLAB=LaB

(10)

RAb=RabLAb=Lab

(11)

RAC=RaCLAC=LaC

(12)

RAc=RacLAc=Lac

(13)

(14)

2.3导芯-护层短路故障

单芯电缆的另外一种常见的故障是绝缘还未完全击穿时的导芯与护层之间的短路故障。假设A相单芯电缆发生导芯-互层短路自恢复故障，其电路原理分析如图6所示。利用电路KVL定理，可得A相单芯电缆回路方程为

(15)

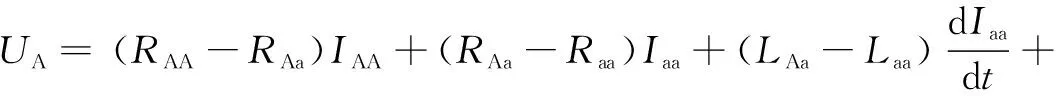
(16)

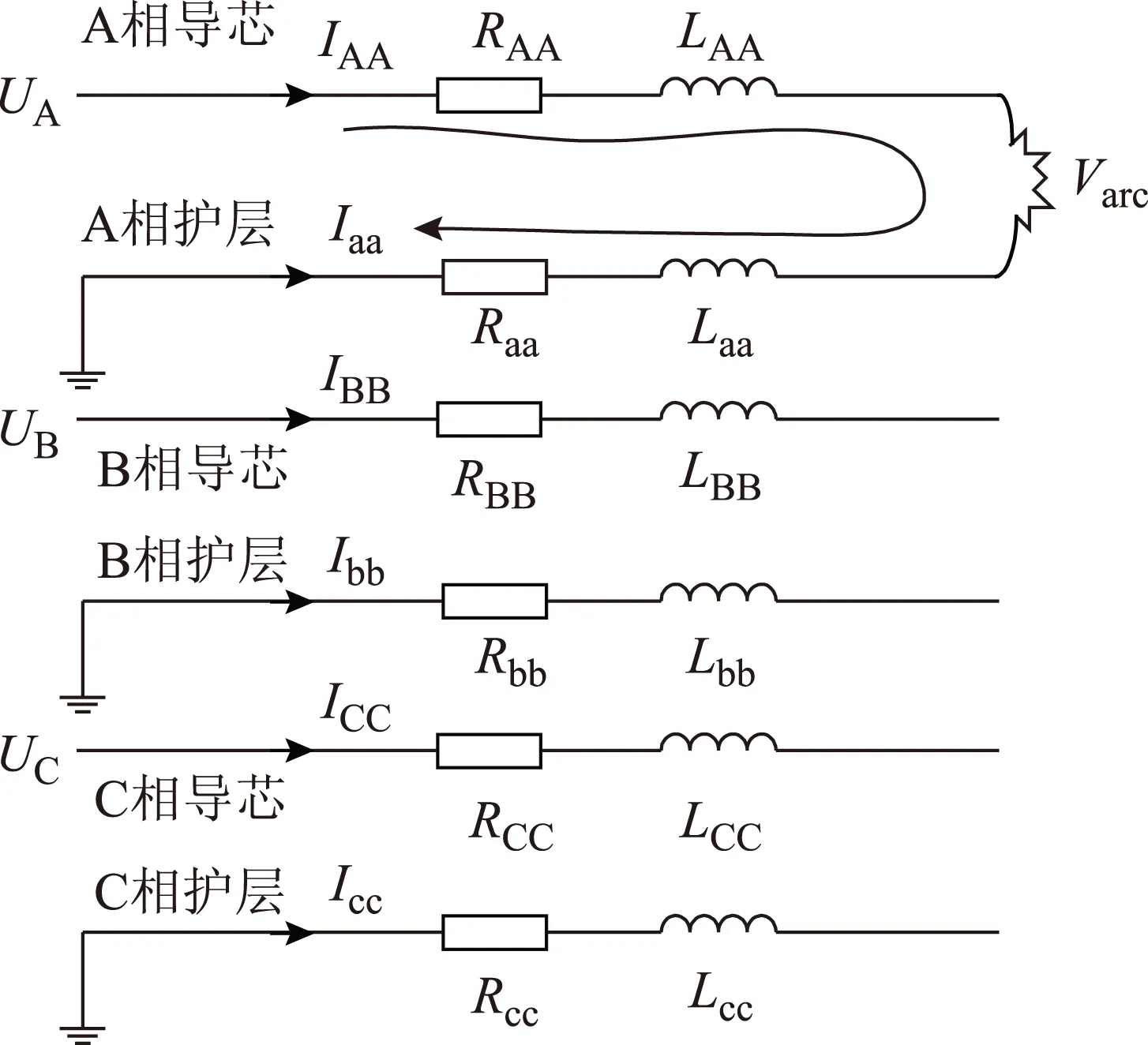
图6　A相导芯-护层短路自恢复故障电路分析Fig.6　The circuit of the core-sheath self-clearing fault in the A phase

3　自恢复故障定位算法

3.1算法流程

由式(14)和式(16)可知，UA、IAA、Iaa可以通过电缆首端的电能质量监测装置得到实时的数据。公式中存在电阻、电感、电弧电压等参数是未知数，其中电路电阻和电感的数值与单位参数、故障距离呈正比。由于采样装置可以采集多点的电压、电流瞬时数据，通过最小二乘回归法即可得到电路的相对稳定的参数估计值。一般情况下，电路电阻容易受到电源内阻和故障电阻的影响，本文采用电路的电感值估计故障距离。

(17)

式中，lAA、lAa分别为A相导芯的单位电感和A相导芯与护层之间的单位互感；Xest为估计得到的自恢复故障点距离。

针对地下电缆线路的自恢复故障定位算法，步骤如下：

1)利用地下电缆首端的电能质量监测装置等波形记录装置，获取电缆线芯的电流和电压以及接地线上的护套电流的波形采样值。

2)选取合适的数据窗口作为自恢复故障定位算法的计算长度，建立故障回路微分方程式。

3)联立数据窗口内的微分方程组，利用最小二乘回归算法，求解方程组内未知常数之一的故障回路电抗值。

4)不断移动数据窗口，重复步骤3，计算线路回路电抗值。如果随着数据窗口的移动，得到的故障回路电抗值估计值稳定在一个恒定值范围，给出电抗值对应的故障距离；否则返回步骤1。

5)通过观察一段时间记录的故障距离曲线，发现某一位置处重复性发生类似自恢复故障，记录故障位置和发生时间频率，并给出预警信号。

本文通过相对误差来评价算法的性能，如式(18)所示。

(18)

式中，Xact为线路故障点到测量点的实际距离；L为线路总长。

3.2仿真模型

在PSCAD/EMTDC中建立10kV系统三相单芯电缆供电模型(横截面积为95mm2)，电缆型号为YJV62-3×(1×95)，电缆长度为10km，如图7所示。由于低压电缆线路长度较短，通常采用电缆互层单端接地或者双端接地的方式。图7中为单端接地模式。

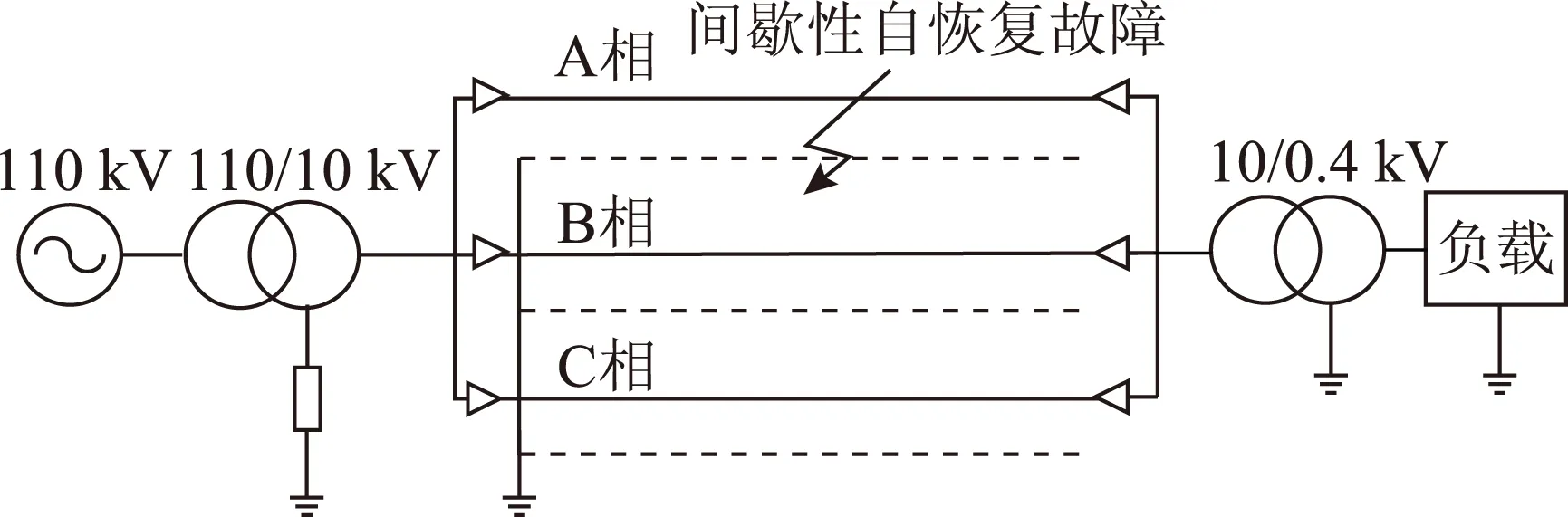
图7　10 kV系统三相单芯电缆拓扑图Fig.7　The topology of the 10 kV three phase system with single-core cables

3.3最小二乘回归过程

为了减小误差，利用多个采样数据，采用最小二乘回归法得到故障回路方程相关估计参数。假设在线路5km处发生5ms自恢复接地故障，采样率为10kHz，以10个采样点为一个数据窗为例，通过最小二乘回归法得到估计参数拟合优度如图8a所示，显著性概率如图8b所示，估计电抗值如图8c所示，对应的故障距离值如图8d所示。由图8可知，利用最小二乘回归法进行自恢复故障回路的参数的估计(前40个有效数据窗内)的显著性概率小于0.05，回归模型成立。拟合优度接近1，回归方程组得到的故障回路电抗估计值和对应的故障距离估计值具有较好的可靠性。

分别通过5～20个采样点回归后得到的故障距离估计误差如图9所示。从收敛后数据仿真显示，用N=5个采样数据得到的估计值误差效果较差。使用N

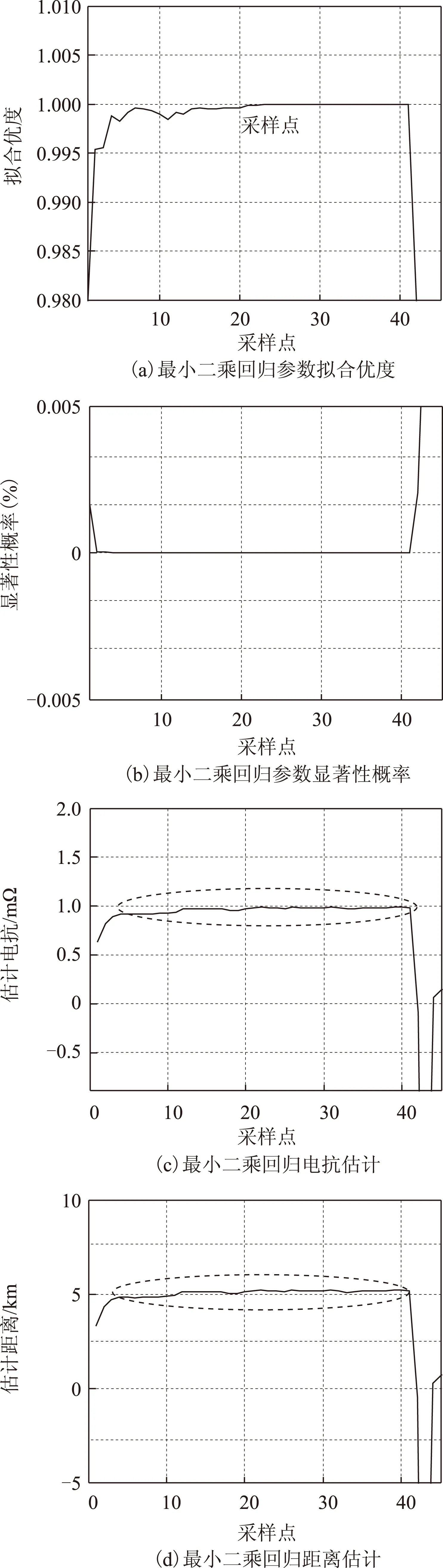
图8　最小二乘回归法得到估计参数过程Fig.8　The process of the parameter estimation by Least Square method

为10、15和20三者均具有较好的结果，但是由于自恢复故障持续时间较短，在故障采样值有限的情况下，数据窗口长度取大后，能够计算的有效的回路电抗值数量将减少。因此，本文后续均采用10个采样点用以自恢复故障距离的估计。

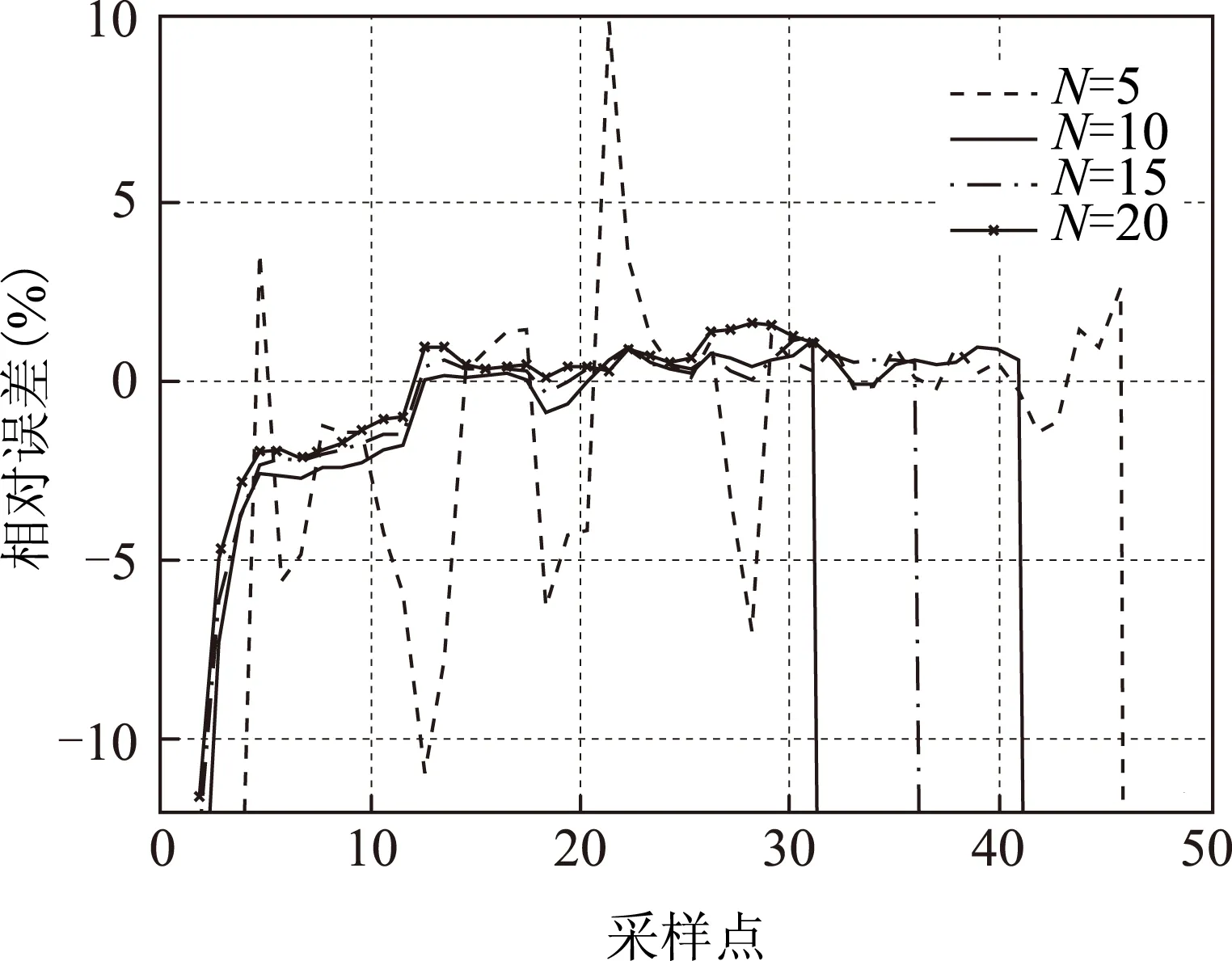
图9　线路5 km处发生自恢复故障的测距误差Fig.9　The error of the estimation in the core-sheath-ground self-clearing fault when the fault distance is 5 km

3.4阻抗模型对比

单层阻抗模型[19]计算时不考虑护层与导芯之间的电气耦合关系。假设电缆发生接地自恢复故障时，两种模型算法下的故障距离估计结果对比如图10所示。图中设置故障距离5 km，自恢复故障持续时间为5 ms。由图10可见，计及护层信息的双阻抗模型相比于文献[19]中提出的算法具有更快的收敛性和准确性。单阻抗模型算法由于受到电缆金属护层耦合的电气影响，估计值存在振荡，估计效果较差。

图10　线路5 km处不同阻抗模型算法估计距离结果Fig.10　The result of the estimation in the core-sheath-ground self-clearing fault under different impedance models

4　算例测试

4.1电缆导芯-护层-大地自恢复故障测试

分别在离首端测量点不同位置处设置5 ms和10 ms 的A相导芯-护层接地自恢复接地故障，故障发生在0.483 8 s，距离估计和平均相对误差见表1。图11为故障持续1/2周期的估计误差情况。

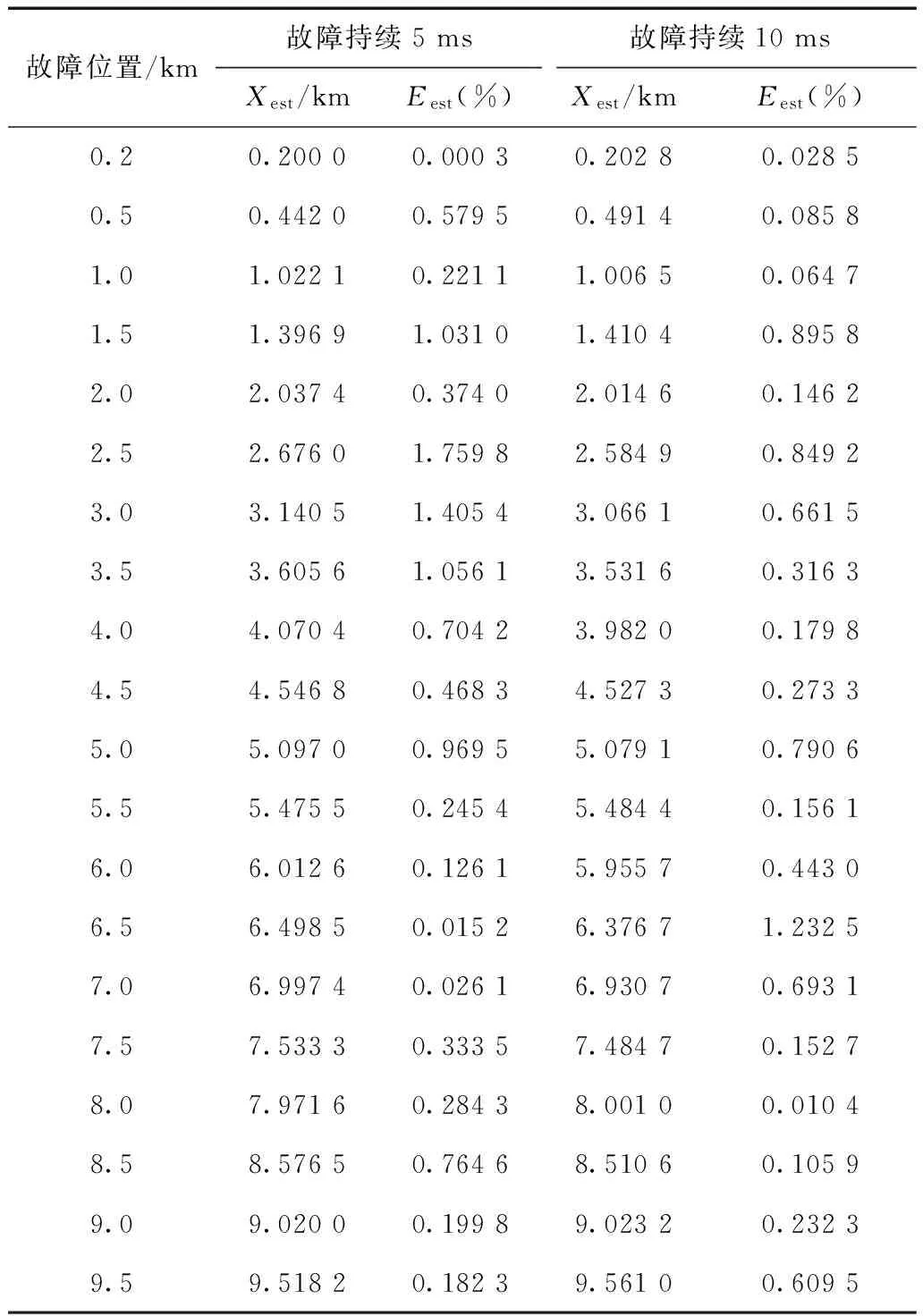
表1　不同故障条件下电缆芯-护套-大地发生 自恢复故障时故障距离估计Tab.1　The result of the estimation in the core-sheath-ground vfault with different fault conditions

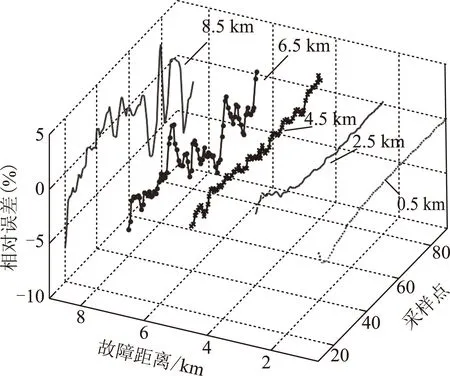
图11　线路不同位置处发生持续时间为二分之一周期的 自恢复故障的测距相对误差Fig.11　The error of the estimation with different fault distance in the core-sheath-ground that the duration time is half of a cycle

图11可知，0.5 km、2.5 km、4.5 km处，估计距离的相对误差曲线趋于平稳。而当故障距离在电缆后部分时(如6.5 km、8.5 km)，估计距离的相对误差曲线上下波动较大。由于本文所列方程是在50 Hz工频下集中参数模型求解，故障发生在线路末端相对故障发生在线路前端时，故障距离更长，受到暂态影响更大。但由于估计距离在真实值附近变化，通过均值滤波器平滑曲线或者计算一定数据窗内的平均值减小估计误差。由表1计算的平均值结果可知，当电缆发生导芯-护套-接地自恢复故障时，估计距离的平均相对误差不超过1.8%，大部分故障距离不超过1%。

4.2电缆导芯-护层自恢复短路故障测试

电缆发生导芯-护层自恢复短路故障，在导芯和护层之间会产生电弧电压。当自恢复故障持续时间较长时，产生的电弧电压在电流过零点时会产生正负交替的现象，如图12所示。电弧电压的幅值正负情况与电弧电流的正负一致。

图13为故障在距离首端5 km时，自恢复故障时间持续5/4周期的估计距离情况。在自恢复故障持续时间内，存在3段较为平稳的估计值分布，不稳定的估计值所在数据窗均在电弧电流过零点前后，即电弧电压幅值出现正负交替的过程。故障距离估计平均相对误差由平稳数据窗下的估计值计算。分别在波峰处(t=0.483 9 s)和波谷处(t=0.473 9 s)设置持续时间为25 ms的电缆导芯与护套之间发生自恢复短路故障，故障距离估计值及平均相对误差见表2。故障发生在9.5 km波峰处时，故障距离误差为1.285 8%；波谷处时，故障距离误差为1.349 5%。其他故障距离下，无论故障发生在波峰还是波谷处，误差均在1%以内。当距离为9.5 km波谷处发生故障时，第一段数据窗的故障距离平均值为9.152 0 km，误差为3.479 6%；第二段数据窗的故障距离平均值为9.445 4 km，误差为0.546 4%；第三段数据窗的故障距离平均值为9.497 8 km，误差为0.022 5%。可见，9.5 km处故障距离误差变大主要是由第一段数据窗内的误差导致。

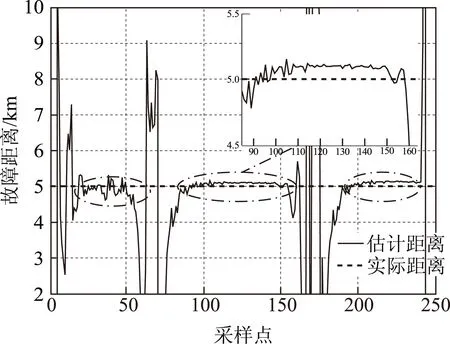
图13　5 km处，电缆导芯-护套自恢复短路故障下的 故障距离估计值Fig.13　The value of the estimation in the core-sheath fault when a distance is 5 km表2　不同故障条件下电缆芯-护套发生 自恢复短路故障时故障距离估计Tab.2　The result of the estimation in the core-sheath fault with different fault conditions

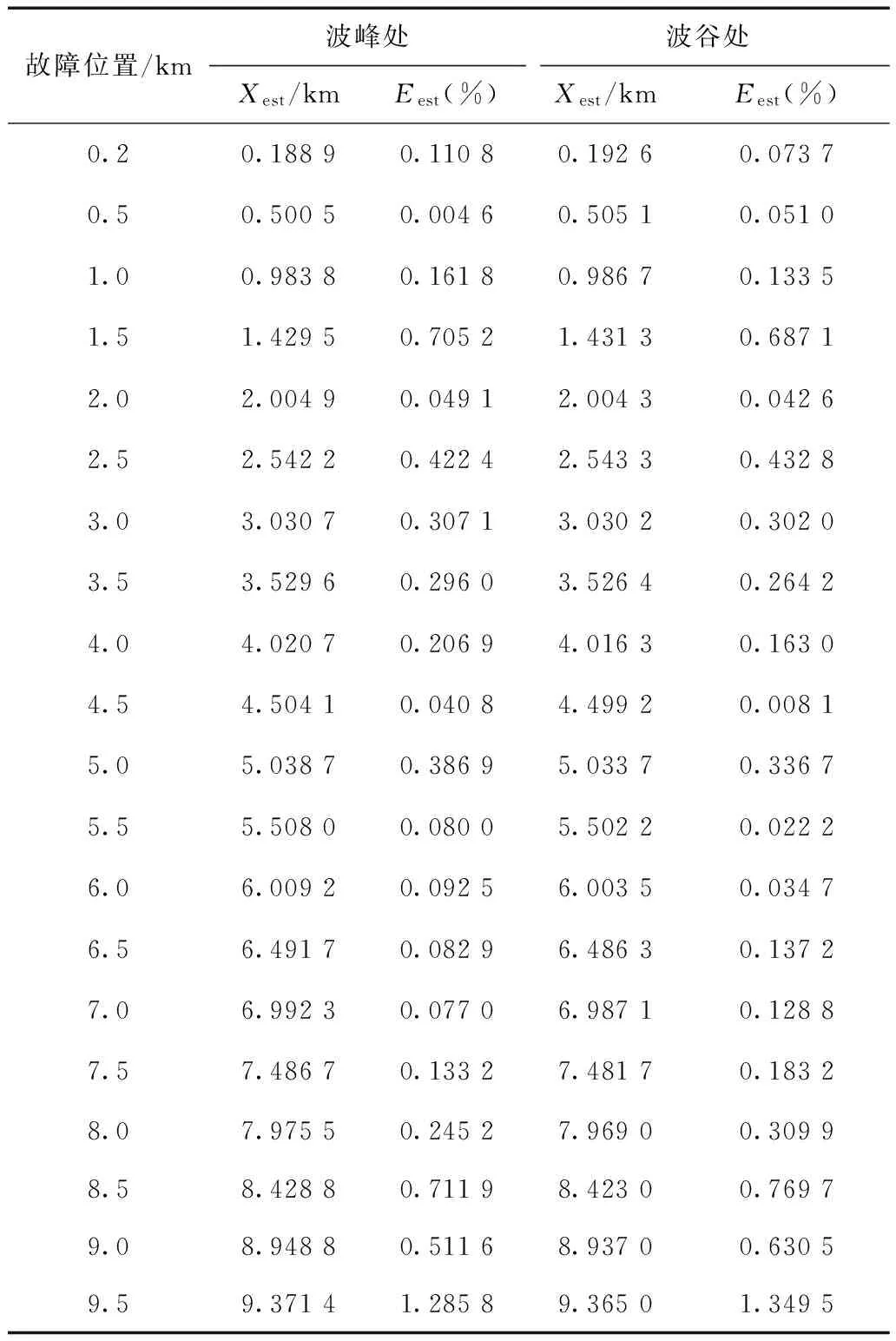
故障位置/km波峰处波谷处Xest/kmEest(%)Xest/kmEest(%)0.20.18890.11080.19260.07370.50.50050.00460.50510.05101.00.98380.16180.98670.13351.51.42950.70521.43130.68712.02.00490.04912.00430.04262.52.54220.42242.54330.43283.03.03070.30713.03020.30203.53.52960.29603.52640.26424.04.02070.20694.01630.16304.54.50410.04084.49920.00815.05.03870.38695.03370.33675.55.50800.08005.50220.02226.06.00920.09256.00350.03476.56.49170.08296.48630.13727.06.99230.07706.98710.12887.57.48670.13327.48170.18328.07.97550.24527.96900.30998.58.42880.71198.42300.76979.08.94880.51168.93700.63059.59.37141.28589.36501.3495

4.3电缆护层接地方式的影响测试

中低压电缆另外一种常见接地方式是金属护层双端接地。表3为电缆护层单双端接地时，在导芯-护层之间发生持续时间为15ms的自恢复接地故障和自恢复短路故障的估计结果对比情况。

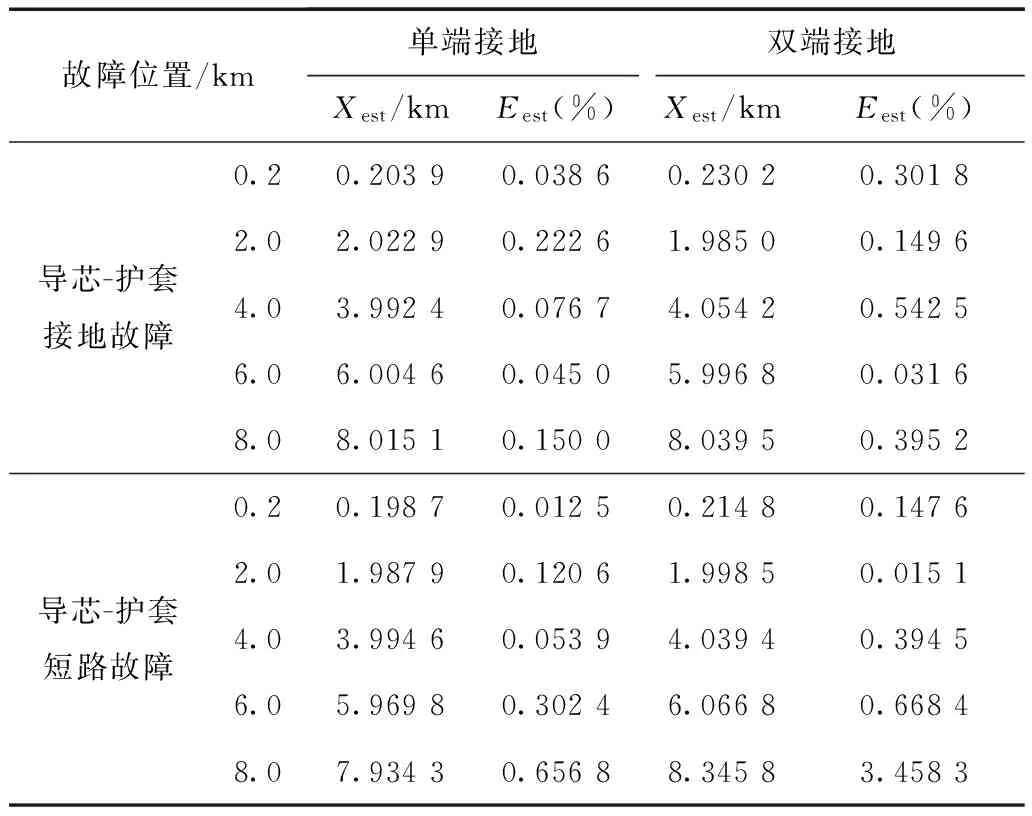
表3　不同故障距离下电缆单端/双端接地 自恢复故障时距离估计结果对比Tab.3　The result of the estimation in the single-ended and double-ended cable systems with different fault conditions

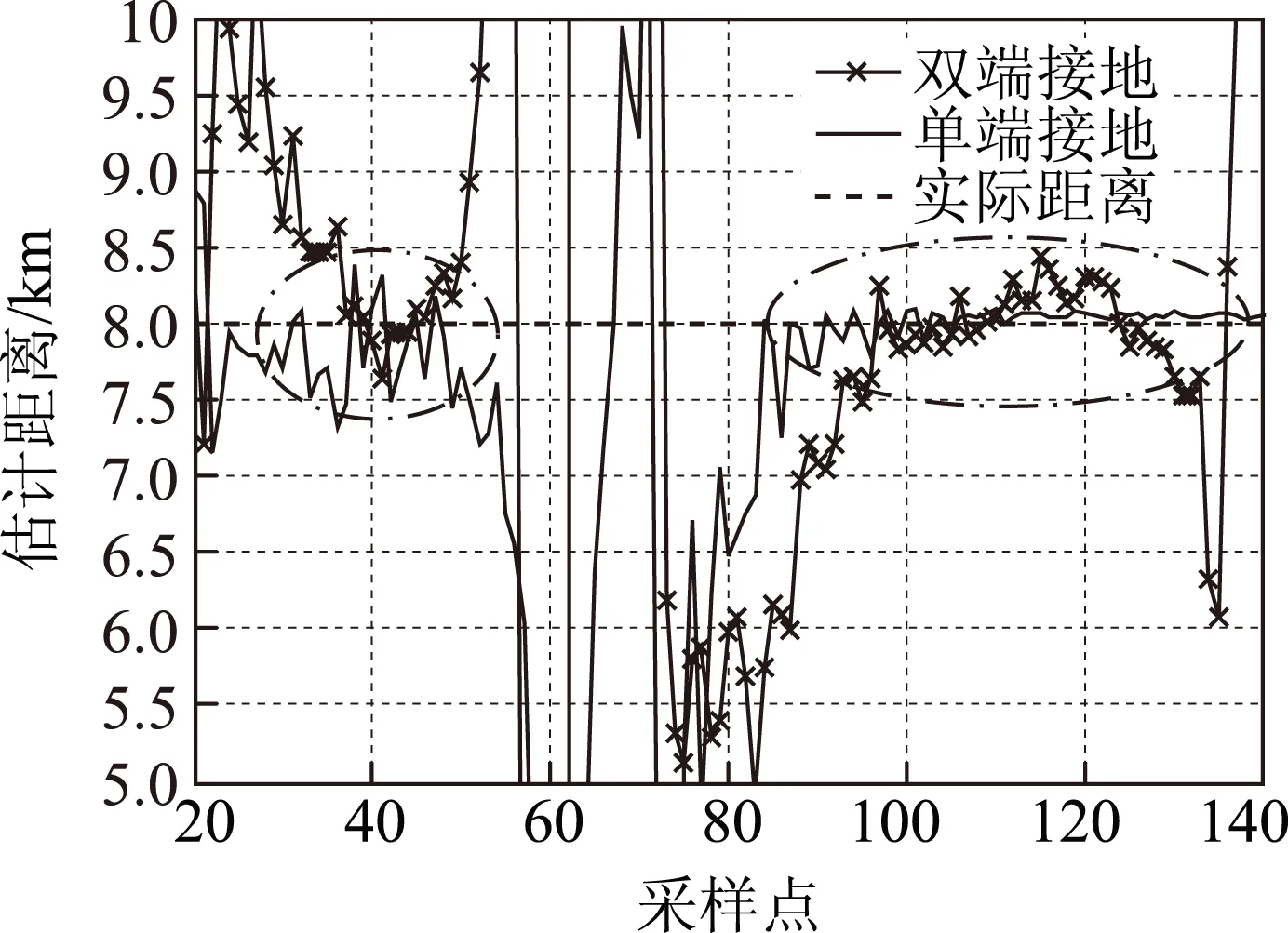
图14　在8 km处，电缆导芯-护套自恢复短路故障下 单端和双端接地的故障距离估计结果对比Fig.14　The result of the estimation in the single-ended and double-ended cable systems when a core-sheath self-clearing fault occurred at 8 km

由表3可知，发生导芯-护套接地故障时，两种接地方式下的故障距离的误差在1%以内。发生导芯-护套短路故障时，在8 km之前，两种接地方式估计结果误差在1%以内。当达到8 km后，双端接地时的误差为345.8 m，而单端接地方式下的误差为65.68 m。此时，两种接地方式下的距离估计曲线如图14所示。可见，双端接地方式下，估计距离值稳定的时间窗相对于单端接地方式要短。表3中的误差是以单端接地方式下稳定数据窗数为标准求取平均，因此导致双端接地方式下8 km后的误差值较大，特别是导致过零点前(故障后5 ms内)的误差值较大。在电缆8 km故障时，在双端接地方式下稳定数据窗内求取的平均故障距离为8.046 6 km，误差为0.466 4%。因此，由于距离估计的稳定时间窗不统一，自恢复故障距离实时估计曲线对发现线路的潜在故障位置更具有参考价值。

4.4分布电容对算法的影响测试

考虑电缆的分布电容影响，对式(14)和式(16)加入了导芯与地、导芯与护层、护层与地之间的分布电容电流。以发生导芯-护套接地故障，持续时间5 ms为例，结果见表4。由表4可知，考虑电容后的距离估计结果并没有明显提高测距的精度。由于考虑电容的影响，使得原有的方程更加复杂，增加了首端电压的一阶导数和二阶导数，会扩大时域计算的误差。

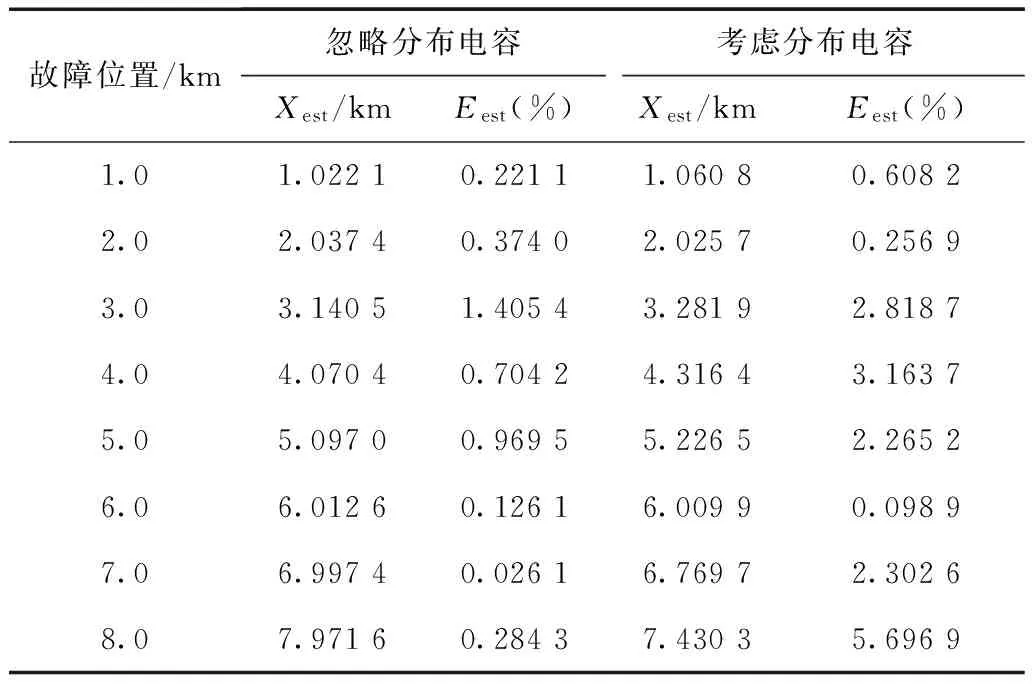
表4　导芯-护套接地故障考虑分布电容影响的结果Tab.4　The result of the estimation with the effect of the distributed capacitance

4.5噪声对算法的影响测试

利用实验室示波器录波信号对电缆导芯-护套自恢复接地故障方法进行测试。测试结果显示，由于示波器录波的波形含有信号噪声，相比于理想波形距离估计结果波动更为明显。由于时域算法中用到差分算子近似微分过程，对噪声具有一定的放大作用，通过前置去噪处理和后置波形处理方法，可减弱噪声干扰对算法的影响程度。

5　结论

本文考虑电缆护层与导芯之间电气耦合的影响，针对电缆失效过程中的自恢复故障进行研究，提出了一种基于双层阻抗模型的三相单芯电缆自恢复故障定位方法。在不增加额外设备的条件下，算法利用电缆首端监测的导芯电流、电压以及护层接地电流波形时域数据，能够准确提取持续时间较短的自恢复故障暂态的有效信息，大量仿真表明：

1)建立的电缆双阻抗模型，能够实现电缆导芯-护层接地故障和电缆导芯-护层短路故障的模拟，较单层阻抗故障模型更能反映电缆金属护层的电气行为，计算结果具有更好的收敛性和准确性。

2)电缆发生导芯-护层接地故障和电缆导芯-护层短路故障时，算法可以快速准确地估计自恢复故障的位置，不受故障位置、故障持续时间和电缆接地方式的影响。

3)所提算法的距离估计结果的稳定数据窗长具有一定的不确定性，自恢复故障距离实时估计曲线对发现线路的潜在故障位置更具有实际参考价值。

[1]许刚，谈元鹏，黄琳.基于低秩矩阵填充的XLPE电力电缆寿命评估[J].电工技术学报，2014，29(12)：268-276.

Xu Gang，Tan Yuanpeng，Huang Lin.Low-rank matrix completion based lifetime evaluation of XLPE power cable[J].Transactions of China Electrotechnical Society，2014，29(12)：268-276.

[2]黄泽华，李锰，刘裕涵.智能配电网自愈控制方案研究[J].电工技术学报，2014，29(1)：492-496.

Huang Zehua，Li Meng，Liu Yuhan.Research of smart distribution network self-healing scheme[J].Transactions of China Electrotechnical Society，2014，29(1)：492-496.

[3]童宁，余梦琪，林湘宁.基于相电流高频特征识别的配电网故障指示器原理[J].电工技术学报，2015，30(12)：465-471.

Tong Ning，Yu Mengqi，Lin Xiangning.Study for fault indicator based on the daulty phase current feature recognition for the distribution network[J].Transactions of China Electrotechnical Society，2015，30(12)：465-471.

[4]姚海燕，张静，留毅.基于多尺度小波判据的和时频特征关联的电缆早期故障检测和识别方法[J].电力系统保护与控制，2015，4(9)：115-123.

Yao Haiyan，Zhang Jing，Liu Yi.Method of incipient faults detection and identification based on multi-scale wavelet criterions and time-frequency feature association[J].Power System Protection and Control，2015，4(9)：115-123.

[5]Kim C，Bialek T，Awiylika J.An initial investigation for locating self-clearing faults in distribution systems[J].IEEE Transactions on Smart Grid，2013，4(2)：1105-1112.

[6]唐金锐，尹项根，张哲，等.零模检测波速的迭代提取及其在配电网单相接地故障定位中的应用[J].电工技术学报，2013，28(4)：203-211.

Tang Jinrui，Yin Xianggen，Zhang Zhe，et al.Iterative extraction of detected zero-mode wave velocity and its application in single phase-to-ground fault location in distribution networks[J].Transactions of China Electrotechnical Society，2013，28(4)：203-211.

[7]梁睿，靳征，王崇林，等.行波时频复合分析的配电网故障定位研究[J].中国电机工程学报，2013，33(28)：130-136.

Liang Rui，Jin Zheng，Wang Chonglin，et al.Research of fault location in distribution networks based on integration of travelling wave time and frequency analysis[J].Proceeding of the CSEE，2013，33(28)：130-136.

[8]刘朕志，舒勤，韩晓言.基于行波模量速度差的配电网故障测距迭代算法[J].电力系统保护与控制，2015，43(8)：88-93.

Liu Zhenzhi，Shu Qin，Han Xiaoyan.An iterative fault algorithm using difference of wave velocity zero mode component and aerial mode component of travelling wave[J].Power System Protection and Control，2015，43(8)：88-93.

[9]张姝，何正友，赵云翾，等.基于C型行波法的10 kV客运专线电力电缆贯通线故障定位方法[J].电力系统保护与控制，2012，40(14)：51-57.

Zhang Shu，He Zhengyou，Zhao Yunxuan，et al.A fault location，method based on C-type travelling wave for the power cable of the 10 kV passenger dedicated line[J].Power System Protection and Control，2012，40(14)：51-57.

[10]李峰，徐丙垠.电弧反射电缆故障测距装置脉冲发射时刻选择算法[J].电力系统自动化，2011，35(13)：88-91.

Li Feng，Xu Bingyin.Pulse emitting time selection algorithm for cable fault locator with arc reflection[J].Automation of Electric Power Systems，2011，35(13)：88-91.

[11]李峰，徐丙垠，颜廷纯.电弧反射法电缆故障测距中的电弧建模与仿真[J].电力系统自动化，2014，38(11)：104-108.

Li Feng，Xu Bingyin，Yan Tingchun.Modeling and simulating of arcs for cable fault location in arc mode[J].Automation of Electric Power Systems，2014，38(11)：104-108.

[12]常文治，葛振东，时翔，等.振荡电压下电缆典型缺陷局部放电的统计特征及定位研究[J].电网技术，2013，37(3)：746-752.Chang Wenzhi，Ge Zhendong，Shi Xiang,et at.Statiistical characteristic and location of partial discharge caused by typical defects in power cable under damped oscillation voltage[J].Power System Technology，2013，37(3)：746-752.

[13]唐昆明，唐辰旭，罗建，等.基于RLC模型参数辨识的配网电缆单相接地故障的单端时域测距方法[J].电力系统保护与控制，2014，42(4)：54-60.

Tang Kunming，Tang Chenxu，Luo Jian，et al.A single-ended time domain fault loation method for distribution network cable single-phase earth fault based on RLC model parameter identification[J].Power System Protection and Control，2014，42(4)：54-60.

[14]索南加乐，宋国兵，康小宁，等.基于单端电流的双回线时域故障定位方法[J].中国电机工程学报，2007，27(7)：52-57.

Suonan Jiale，Song Guobing，Kang Xiaoning，et al.A time-domain fault location algorithm based on one-terminal current of parallel transmission lines[J].Proceeding of the CSEE，2007，27(7)：52-57.

[15]Xu Z，Sidhu T S.Fault location method based on single-end measurements for underground cables[J].IEEE Transactions on Power Delivery，2011，26(4)：2845-2854.

[16]Rafinia A，Moshtagh J.A new approach to fault location in three-phase underground distribution system using combination of wavelet analysis with ANN and FLS[J].Electrical Power and Energy Systems，2014，55(2)：261-274.

[17]Todorovski M，Ackovski R.Equivalent circuit of single-core cable lines suitable for grounding systems analysis under line-to-ground fault[J].IEEE Transactions on Power Delivery，2014，29(2)：751-759.

[18]Alamuti M M，Nouri H，Ciric R M，et al.Intermittent fault location in distribution feeders[J].IEEE Transactions on Power Delivery，2012，27(1)：96-103.

[19]Kulkarni S，Santoso S，Short T A.Incipient fault location algorithm for underground cables[J].IEEE Transactions on Smart Grid，2014，5(3)：1165-1174.

[20]Kulkarni S.Fault location and characterization in AC and DC power systems[D].Austin：The University of Texas at Austin，2012.

[21]束洪春，司大军，葛耀中.高压输电线路电弧故障检测与定位最小二乘法新解[J].电工技术学报，2000，15(5)：63-68.

Shu Hongchun，Si Dajun，Ge Yaozhong.A new least error square method for detecting and locating arc fault in EHV transmission line[J].Transactions of China Electrotechnical Society，2000，15(5)：63-68.

[22]王钢，徐子利，梁远升，等.基于电弧方波曲线相似度的输电线路单端故障测距时域算法[J].电力系统保护与控制，2012，40(23)：109-113.

Wang Gang，Xu Zili，Liang Yuansheng，et al.Single terminal time domain fault location method based on the similarity of square wave for arc grounding fault[J].Power System Protection and Control，2012，40(23)：109-113.

Fault Location of Self-Clearing Fault in Three Phase Single Core Cables Based on Double Impedance Model

Zhang ShuLin ShengTang JinHe Zhengyou

(School of Electrical EngineeringSouthwest Jiaotong UniversityChengdu610031China)

The failure process of the underground cable also accompanies the periodical self-clearing faults.Fast and accurate location of this kind of fault can find the potential fault points before a permanent breakdown，which provides the basis for operation and maintenance of underground cables.An algorithm for locating the self-clearing fault based the double impedance model in the three phase single core cables has been proposed that considers the impact of the metal sheath.The circuit equations of the core-sheath-ground self-clearing fault and the core-sheath self-clearing fault have been derived based on the double impedance model.The proposed method uses the time-domain information of the current and voltage waveforms monitored in the head-end of cables.The self-clearing fault can be located by the least squares regress method during a short time.Extensive simulations show that the algorithm，considering the behavior of the metal sheath of cables，can locate the self-clearing fault accurately.The proposed method is more consistent with actual structure of cables than the methods only consider the impedance of the core and it can explain the electrical behavior between the conduction and metal sheath of coaxial cables.

Single-core cable，metal sheath，self-clearing fault，double impedance，fault location

2015-05-26改稿日期2015-07-30

TM77

张姝女，1988年生，博士研究生，研究方向为配电网故障诊断。

E-mail：ZS20061621@163.com

林圣男，1983年生，博士，副教授，研究方向为输配电网故障诊断。

E-mail：slin@home.swjtu.edu.cn(通信作者)

国家自然科学基金(51307145)和四川省应用基础计划(2014JY0177)资助项目。