基于虚拟电价的电动汽车充放电优化调度及其实现机制研究

杨晓东　张有兵　翁国庆　赵　波　高　翔

(1.浙江工业大学信息工程学院　杭州　310023 2.国网浙江省电力公司电力科学研究院　杭州　310014 3.国网浙江省电力公司丽水供电公司　丽水　323000)



基于虚拟电价的电动汽车充放电优化调度及其实现机制研究

杨晓东1张有兵1翁国庆1赵波2高翔3

(1.浙江工业大学信息工程学院杭州310023 2.国网浙江省电力公司电力科学研究院杭州310014 3.国网浙江省电力公司丽水供电公司丽水323000)

提出了基于虚拟电价理论的电动汽车(EV)充放电优化调度思想，构建了以削峰填谷为目的、兼顾配电系统负荷信息与用户电能损失费用及电池损耗成本的EV充放电优化调度和实现机制模型。在所建的模型中，通过虚拟电价将充放电功率与系统负荷信息相关联，并研究了根据虚拟花费最小进行EV充放电优化的功率调节方法。在此基础上，综合小波分析和模糊聚类确立了用于EV充放电的动态分时电价机制，以保障调度策略的可实施性。最后，以某小区充电设施集群为例对5种优化模式进行了仿真分析，算例结果说明了所述模型的基本特征。

电动汽车虚拟电价削峰填谷充放电优化功率可调实现机制

0　引言

化石燃料的储备不足及全球气候变暖被日益关注，环境观念的提升使人们强烈要求在交通方面减少石油消耗。这种契机下，因具有良好的节能和低排放潜力，电动汽车(Electric Vehicle，EV)得到广泛的发展[1-3]。

负荷峰谷差是电力系统运行的一项重要、安全、经济指标，峰谷差的加剧，会带来电网设备利用效率降低、供电侧购电风险增加等不良后果[4]。为推进高峰负荷转移、缓解电力供应紧张的局面，2012年国家财政部和发改委批复开展首批需求侧管理试点工作[5]。

交通系统的电气化使车辆的能量需求从化石燃料逐渐转移至电力系统，这将对电网产生重大影响。到2025年，全球年出售的电动汽车规模渗透率将达10%[6]，大量电动汽车随机接入电网进行无序充电，会进一步加剧系统负荷峰谷差，对配电网的运行状态带来负面影响[7-9]。

合理控制接入配电网的电动汽车充放电，可以降低大规模电动汽车充电对电网造成的影响。目前，国内外针对电动汽车有序充放电的研究成果已有很多。文献[10]以削减负荷峰值为目标，对电动汽车进行有序充电控制。文献[11]考虑电动汽车入网(Vehicle to Grid，V2G)服务，提出采用虚拟电价-动态规划方法(virtual Time-of-Use tariffs Dynamic Programming，vTOU-DP)优化特定变压器容量约束下的电动汽车充放电功率，具有优越的削峰填谷作用。文献[12]建立了以降低负荷峰值和平滑负荷波动为目标的电动汽车有序充放电模型，可以有效地转移高峰负荷，对电力系统的规划管理及对EV用户的激励政策制定有一定的参考价值。文献[13]考虑变压器容量、负荷峰谷差和节点电压稳定情况等配电网约束进行电动汽车的有序充电控制，可以在现有配电网条件下接入尽可能多的电动汽车。文献[14]提出通过两阶段优化方法对电动汽车进行充放电控制，分别用于减少充放电代理商的运营费用和降低负荷波动。该类方法往往仅以实施方的角度进行直接负荷控制，旨在满足实施方需求，缺乏对用户的考虑，难以得到用户的认可和实际应用。

随着市场经济及需求侧管理[15，16]的深入发展，为吸引用户参与充放电优化，如何协调供需两侧的利益，制定充放电策略成了新的研究热点。文献[17]以减小电网峰谷差为主要目标设计了基于分时电价的电动汽车充电策略，但易造成过响应现象。文献[18]提出基于动态分时电价的有序充电策略，实现了充电负荷削峰填谷，降低了用户充电成本。文献[19]基于对策论提出一种针对电动汽车充电的需求响应策略，可以在降低用户充电费用的同时实现系统优化用电。但文献[17-19]均未考虑V2G的作用。文献[20]引入分层分区调度理念，构建了基于双层规划的电动汽车两层智能充放电模型，实现了运营商、电网和用户三者之间利益的有机协调。文献[21]以用电成本最小为目标建立了分散式电动汽车充放电博弈模型，提高了用电经济性，并改善了系统负荷特性。上述研究往往以额定功率实施充电或充放电控制，缺少对充放电功率进行连续调节的考虑，在优化深度上还存在发展与完善的空间。文献[22]以公共虚拟电价信号和充电迫切程度为依据提出单辆车充放电功率的自动调整方法，并据此侧重研究了电动汽车的平抑风电出力波动以及调频作用，其并未着眼于稳定网供功率、发挥车辆集群的削峰填谷作用。

在上述背景下，本文以削峰填谷为目的，面向局域配电网对电动汽车充放电优化调度方法及其实现机制进行了研究。基于虚拟电价理论建立了以充放电功率为优化变量的优化调度模型；综合小波分析和模糊聚类确定了用于电动汽车充放电的动态分时电价机制，从而提供一种吸引车主的激励措施，保障调度策略的可实施性。以某小区充电设施集群为例的仿真结果证明了所提方法的有效性和可行性。

1　电动汽车充放电调度架构及调度流程

1.1优化调度架构

本研究面向局域配电网建立基于虚拟电价的电动汽车充放电优化调度模型(virtual Time-of-use tariffs based Optimal Scheduling considering Continuously Adjustable Power，CA-vTOS)，其调度架构如图1所示。

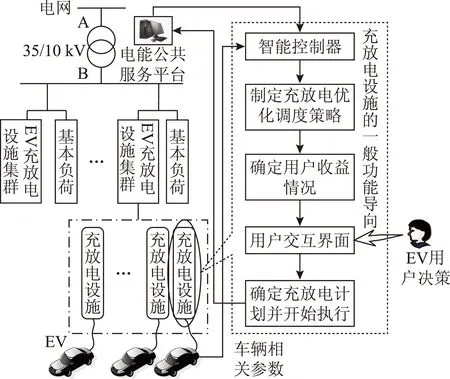
图1　优化调度架构Fig.1　Architecture of optimal scheduling method

电能公共服务平台的功能描述：该局域配电网内，公共服务平台收集变压器B端的负荷信息，一方面，用于向该区域内的充放电设施发布实时负荷信息；另一方面，接收各充放电设施的计划负荷予以整合，以便实时更新负荷信息。

1.2电动汽车充放电优化调度实现流程

以虚拟电价理论为媒介研究了关联系统负荷水平的电动汽车充放电功率动态和连续调整方法，并配套发展了保障调度实现的动态分时电价机制，优化调度及实现流程如图2所示。

图2　优化调度流程图Fig.2　Flow chart of the proposed CA-vTOS

结合图2，当有新的电动汽车接入该配电网时，充放电设施按以下步骤进行电动汽车充放电的调度及实现。

1)获取电动汽车充电相关信息：读取接入时间、电池初始荷电状态(State of Charge，SOC)。需要车主告知预期离开时间以及离开时的期望SOC。

2)制定充放电计划并确定用户成本：根据车辆充电相关信息，以当前负荷水平为基础，基于虚拟电价理论制定满足优化调度模型的车辆充放电计划。结合充放电计划与发展的动态分时电价机制确定用户成本。

3)用户自主响应充电模式：将充放电计划及具体收益情况告知用户，由用户自主响应充电模式，选择响应调度计划或开始无序充电，充放电设施根据用户选择对电动汽车实施具体充放电操作。

通过以虚拟电价为理论依据的优化调度发挥电动汽车的负荷转移潜力，能够实现系统的优化用电，同时采用所发展的电价机制，激励用户参与调度，为所建模型提供一种实现机制，有利于实现电力供需和用户经济效益的双向均衡。

2　虚拟电价理论与动态分时电价机制

2.1虚拟电价理论

大规模电动汽车接入电网进行无序充电是一种不合理的用电方式，为缓解高峰负荷需求压力，分时电价理论得到了实际应用，对应地，基于分时电价的电动汽车充放电优化方法可以在有限条件下有效转移高峰负荷[14，17]。然而，文献[23]指出我国电力交易仍以计划性机制为主，导致电价形成机制不完善，制约了电力资源利用效率的提高。由国务院发布的关于深化电力体制改革的意见[24]中指出，在市场化电价机制尚未完全开放的情况下，现有电价机制往往难以反映市场供需状况。因此，以现有静态分时电价理论为依据开展电动汽车的优化调度，可能会导致期望外的、新的负荷高峰出现，与优化初衷相悖。

针对上述问题，为充分挖掘电动汽车集群负荷的削峰填谷潜力，同时避免出现峰谷倒置等不良后果，本文借鉴静态分时电价理论对电动汽车集群负荷的引导作用，发展了虚拟电价相关理论，以虚拟电价为手段间接反映负荷水平。

相对于静态分时电价，虚拟电价的一个显著特点是动态更新，能够实时反映供需关系。除此之外，虚拟电价不受现存电力体制的限制，摆脱了我国电价体制改革步伐缓慢的约束。虚拟电价在模型中仅作为制定车辆充放电计划的依据指标，用以确定每辆车的最佳充放电计划，并不用于计算实际成本。

为方便起见，将连续的时间进行离散化处理，将一天均分为J个时段，每个时段时长为Δt。虚拟电价和负荷信息的关系为

(1)

(2)

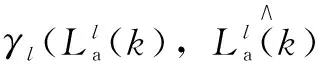
(3)

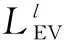
由式(1)、式(2)可得

(4)

可见，总体上虚拟电价与当前负荷水平呈正相关性，是关联电动汽车交互功率与负荷水平的媒介。其次，虚拟电价不局限于数值的大小，仅需满足价格序关系即可便捷地设定，价格序关系指满足前已述及的虚拟电价与负荷水平的正相关性，即较大的负荷值需相应设定较大的虚拟价格。此外，虚拟电价是针对单辆电动汽车单独设定的，各车辆均享有其私有的虚拟电价，方便精细化实施电动汽车充放电调度。

2.2保障调度实现的动态分时电价机制

虚拟电价可以在一定程度上实时、定量地反映负荷水平，为调度车辆动力电池功率实施削峰填谷提供一种依据。但是，需要说明的是，虚拟电价和实际电价可能并不处于同一金额比例，因而不适用于用户成本的计算。市场经济下，电力用户也是独立的经济体，为了使优化得到的调度策略被电动汽车用户所接受，还需要一种吸引车主的激励措施，以支撑所述模型的实际可实施性。

电动汽车参与V2G服务会给锂电池带来额外的寿命损耗成本，同时会造成更多的电能损失，固定电价无法补偿用户的损失。而用于电动汽车充放电的静态峰谷电价，难以反映市场供需状况，当接入电动汽车规模较大时，对于负荷曲线平滑后接入的电动汽车而言，在优化目标的作用下，可能不会在基本负荷谷时段充电、基本负荷峰时段放电，此时，用户的收益将无法保证。

为匹配优化得到的充放电功率、给予所有参与调度的用户一定的利益反馈，保障调度的真正实现，本文提出用于电动汽车充放电的动态分时电价机制。这里，动态分时电价指高峰、低谷电价固定，峰谷时段变化的电价机制，表示为pril(k)， 其中，高峰电价为prih， 低谷电价为pril， 动态匹配虚拟电价，与车辆l一一对应，随车辆入网过程实时更新。期望以该机制，使用户在电动汽车放电的阶段享受高峰电价，在充电功率较大阶段享受低谷电价，从而降低充放电成本。据此，依据虚拟电价理论确定车辆充放电计划，实现系统的优化用电，而动态分时电价机制用于结算用户成本，保障用户利益，为调度模型提供一种实现机制。

同虚拟电价，实现机制以配电网当前负荷信息为基础，在电动汽车接入时间内，利用小波分析和模糊聚类方法对用于电动汽车充放电的分时电价进行峰谷时段划分：

1)预处理：用小波分析进行预处理，将负荷信息进行尺度为3的小波分解，将一、二层的高频分量置零，重构后得到新的负荷信息，以避免负荷信息中局部突变数据对模糊聚类分析的不良影响。

2)时段划分：针对预处理后的负荷信息，利用模糊聚类方法[25]进行动态分时电价的峰谷时段划分。

3　基于虚拟电价的电动汽车充放电优化调度模型

3.1调度架构中主要单元建模分析

1)V2G模式的电动汽车充放电功率模型。

Xl=[Tin,l,Tout,l,S0,l,SE,l,Cs,l,Pc,l,Pd,l]

(5)

式中，Tin,l、Tout,l分别为车辆l接入电网的时间和预期离开电网的时间；S0,l、SE,l分别为车辆动力电池的起始SOC和离开电网时的期望SOC，SOC为电池剩余能量与电池容量的比值，因此有0≤S0,l≤1、 0≤SE,l≤1；Cs,l为电池容量；Pc,l、Pd,l分别为额定充、放电功率。

设车辆l接入电网的持续时间为Tpe,l=Tout,l-Tin,l， Tpe,l所包含的时段集合(各元素按时段号大小升序存放)设为Tm,l， 并设其长度为Nl。 为表示各时段对车辆电池的可操作性，引入变量

(6)

V2G模式下，任一k时段，电动汽车与配电网的功率交换用pl(k)表示，pl(k)>0表示车辆l处于充电状态；pl(k)<0表示处于放电状态；pl(k)=0表示处于浮充状态。则在Tpe,l时期，车辆的实际充放电功率为

Pl(k)=pl(k)fm,l(k)

(7)

式中，Pl(k)为优化变量，具备连续可调的特性，通常还要受到动力电池或充电机的额定充、放电功率的限制，满足约束

-Pd,l≤Pl(k)≤Pc,l

(8)

当整个研究时段的充放电状态及对应的交换功率优化完成后，充放电计划即制定完成，车辆l的充放电计划由式(9)表示。

(9)

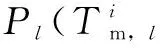
(10)

式中，Ml-1为车辆l接入电网时，充放电计划制定已完成的车辆集合。

2)动力锂电池模型。

优化变量Pl(k)最终转换成能量映射到动力电池的荷电状态上，从而有条件考量是否满足用户充电需求并完成能量计费等相关工作。

电动汽车的众多动力电池种类中，锂电池因性能优良，获得了飞速的发展[26]。本文假设参与调度的电动汽车动力电池均为锂电池。根据锂电池的充放电相关特性[27，28]，为简化起见，在单个时段内，锂电可视为是恒功率充放电。忽略锂电池的自放电率，其荷电状态和对应的充放电时间近似呈线性关系

(11)

式中，Sl(k-1)、Sl(k)分别为电动汽车l在第k-1、k个时段的荷电状态；η(Pl(k))为功率交换效率，与功率交换方向有关。

(12)

式中，ηc、ηd分别为充、放电效率。

3)V2G模式下电动汽车用户成本分析。

V2G模式下，电动汽车用户的成本由3个部分组成，如式(13)所示。

(13)

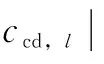
(14)

电动汽车因参与V2G服务而进行频繁的充放电会影响锂电池的使用寿命[27，29]，对锂电池造成的寿命损耗折算成本建模为

(15)

(16)

(17)

式中，φd,l为每单位(kW·h)放电量造成的电池退化成本；cb为每单位电池容量的购置成本；cL为电池置换费用；Bcl为在某一放电深度(DepthofDischarge，DOD)下的电池循环次数；Edis,l为计算时间长度内电池的总放电量；εf为损耗成本系数。

由于充、放电效率的存在，电动汽车与电网进行功率交互时，会造成一定的电能损失。电能损失各组成部分的物理含义及关系示意如图3所示。图中Smax、Smin为保障电池的寿命而设定，分别表示允许的动力电池荷电状态的最大值和最小值。

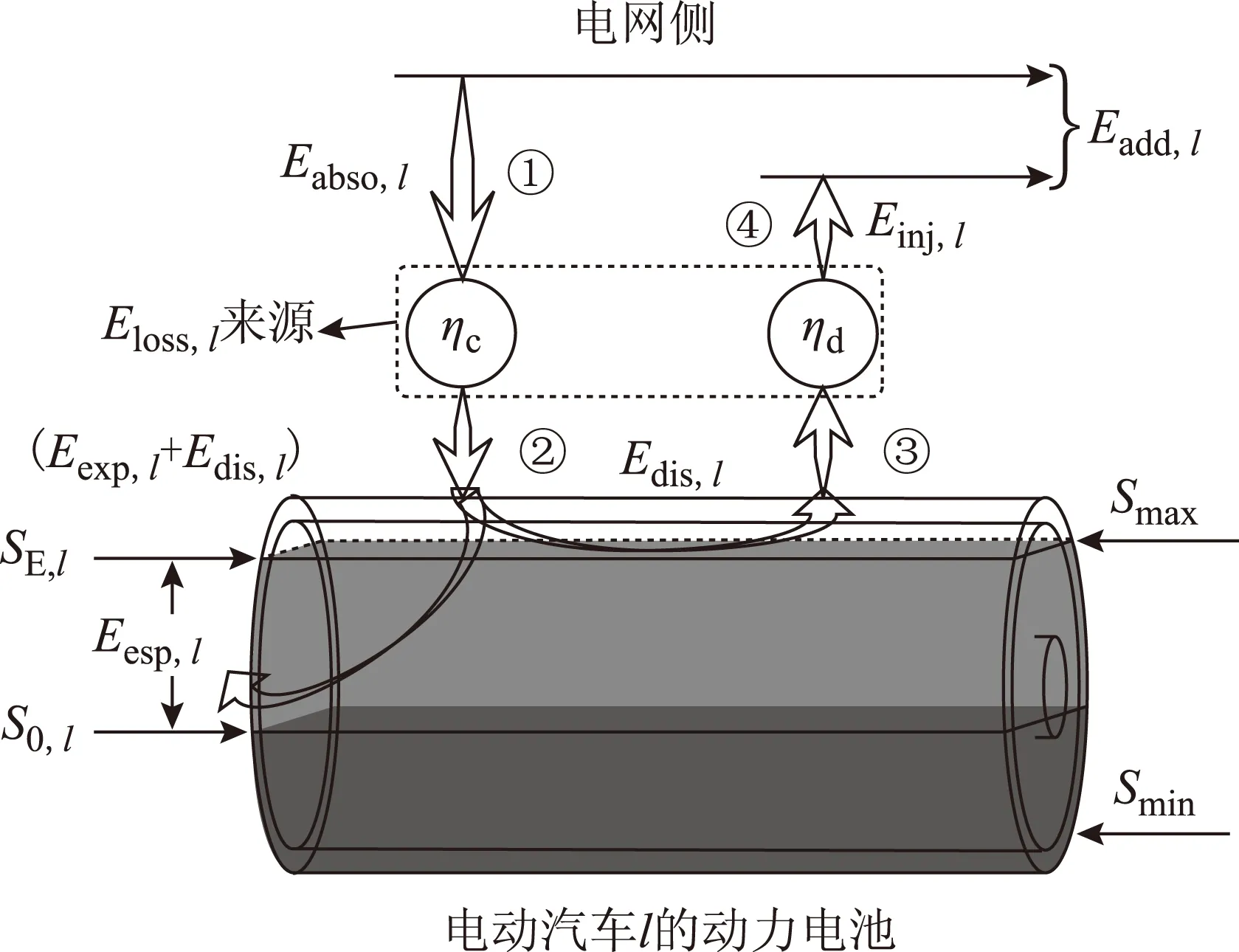
图3　电能损失的物理含义示意Fig.3　The meaning schematic of energy loss

对于∀l∈N， 设Einj,l表示其在计算时间长度内注入电网的总电量，Eabso,l表示从电网吸收的总电量，Eexp,l表示车主的总充电量需求。根据式(12)所示的车辆功率交换效率，向电网注入Einj,l的电量，需要动力电池放出Einj,l/ηd的电量，即Edis,l=Einj,l/ηd； 结合车主的充电量需求，优化期间车辆l动力电池需充入的总电量为Eexp,l+Edis,l， 同样地，计及功率交换效率后有：Eabso,l=(Eexp,l+Edis,l)/ηc； 进一步，电网端实际供给的电量Eadd,l=Eabso,l-Einj,l。

电网端实际供给的电量与车主的需求电量(即车辆离开时电池增加的电量)之差为电能损失，综合图3及上述分析，电能损失量Eloss,l具体表示为

Eloss,l=Eabso,l-Einj,l-Eexp,l

(18)

从各时段能量流动角度分析，可进一步将电能损失分为充电损失量和放电损失量。结合图3，任意时段，能量流动方向仅为①→②、③→④和无流动中一种，于是，Eloss,l又可表示为

(19)

展开式(19)，结果与式(18)一致。对应于能量流动状态，对于∀k∈Tm,l， 其电能损失量eloss,l(k)仅为充电损失量和放电损失量中的一种，并且可通过该时段功率计算得到。因此，电能损失费用为

(20)

3.2优化调度模型

根据车辆的相关参数，期望通过所发展的优化调度模型在满足用户充电需求及变压器限制的条件下，实现电动汽车负荷的削峰填谷。以最小化虚拟充放电成本为目标来优化电动汽车的充放电功率，构建模型为

(21)

s.t.Smin≤Sl(k)≤Smax

(22)

(23)

(24)

Tpe,l>Tc,l，l=1,2,…,n

(25)

式中，Vl为车辆l的虚拟充放电成本；κT为变压器效率；AT为变压器的额定容量；Tc,l为充电至期望电量水平所需的最短时间。

(26)

过充电和过放电都会严重缩短锂电池的寿命，因此，式(22)将受控车辆k时段的荷电状态Sl(k)限定在一定范围内。式(23)表示充电需求约束，车辆如约离开时，其电池的荷电状态需满足期望。式(24)表示变压器最大负载约束，即全天各个时段的总负荷不大于变压器的最大负载，以确保配电系统的安全可靠运行。式(25)为时间关系约束，表示只有当车辆接入电网的持续时间大于充电至期望电量水平所需的最短时间时，车辆才能参与到充放电调度中。

电能具有商品属性，其在被车辆集群消费的过程中，接受优化模型的能量调度，除了要实现削峰填谷作用，还要响应国家能源高效利用的号召，减少电能损失；同时，需保障用户收益，确保调度模型的实现。因此，本文以V2G模式下电动汽车用户成本、电能损失量作为指标评价调度结果的相关性能。

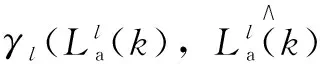
4　算例分析

4.1算例参数

以一处于居民区的充电设施集群为例验证本文所提电动汽车充放电优化调度及实现机制的有效性。接入变压器容量为750kV·A，效率为0.95。该变压器下带有基本负荷和电动汽车集群负荷，最高基线负荷占配电变压器最大负载的80%。根据该居民区基本负荷信息的特征，为了尽可能使虚拟电价与居民区峰谷电价处于同一金额比例，设φ0为-0.21；priR,1、 priR,2分别取低谷电价和高峰电价；φR,1取低谷负荷均值405.1019、φR,2取高峰、低谷负荷均值之差75.7441。

实际上，目标区域内电动汽车集群的充电行为特征具有一定的概率特性。根据北京市交通出行实地调研结果[18，30]，设电动汽车用户早上离开住所时间点服从正态分布(期望值为7∶45，标准差为1h)；下午回到住所的时间点服从正态分布(期望值为19∶00，标准差为1.5h)；回到住所时，车辆动力电池荷电状态服从正态分布(期望值为0.6，标准差为0.1)，并设电动汽车的充放电起止时间、起始SOC等参数相互独立。

4.2比较项设置

为了更好地说明基于虚拟电价的充放电优化调度方法的控制效果，本文同时仿真计算以下4种控制模式，与所提调度方法作对比：

1)无序充电模式，充电设施为接入的电动汽车提供持续的恒功率充电服务，直到用户离开为止，如果在此之前电动汽车电池已经充满，则停止充电。

2)OC-TOU(Optimal Control based on the TOU)，固定分时电价下，以最小化用户成本为目标、功率连续可调的充放电优化模式。采用前文所述模糊聚类方法对基本负荷进行时段划分，所得结果为0∶00～8∶00为电价低谷时段，8∶00～0∶00为电价高峰时段。

3)CP-vTOS(virtual Time-of-use tariffs based Optimal Scheduling considering Constant Power)，动态分时电价下，恒功率有序充放电优化模式(仅额定功率)，即Pl(k)∈[-Pd,l,0,Pc,l]。

4)仅充电优化调度模式，动态分时电价下，不考虑V2G，仅进行功率连续可调的有序充电优化，此时，有0≤Pl(k)≤Pc,l。

4.3仿真结果及分析

基于蒙特卡洛仿真方法模拟电动汽车的充电行为，根据前文所述的电动汽车日充电需求数据分布情况，随机抽取车辆初始SOC、充电起止时间，根据本文提出的优化模型，用Matlab和lingo进行建模、求解，并就以上5种优化模式下的用户充电经济性和负荷曲线进行计算和比较。采用蒙特卡洛仿真方法的模拟结果表明，600次后车辆集群负荷平均值基本保持不变，为平衡计算时间和计算精度，确定仿真次数为600次。叠加基本负荷和电动汽车集群负荷得到日总负荷曲线，如图4所示。进一步的统计信息见表1。

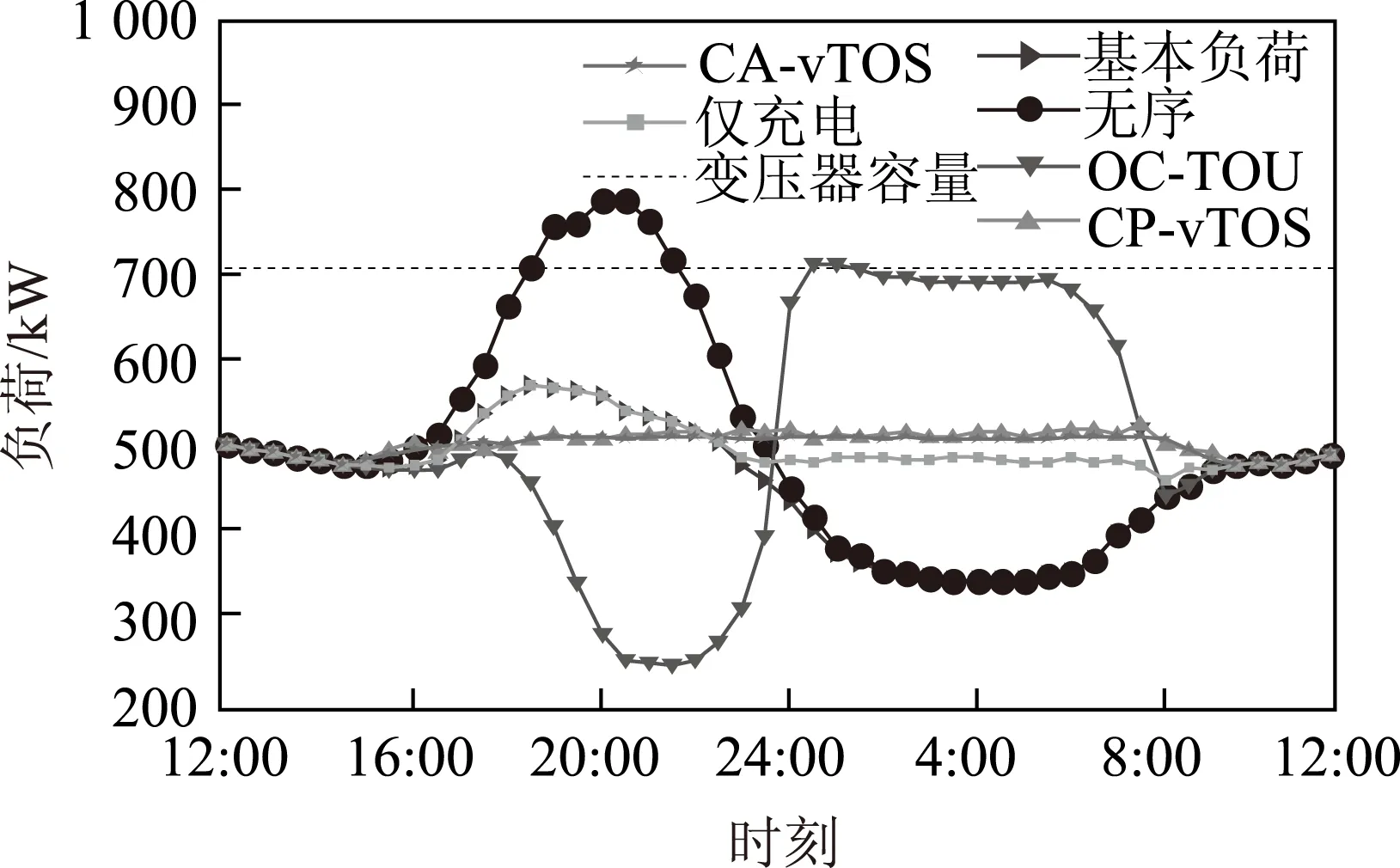
图4　无序和有序优化模式下的负荷曲线Fig.4　Load curves under uncoordinated and coordinated optimization methods表1　无序与有序优化效果统计信息Tab.1　Results of uncoordinated and coordinated optimization methods

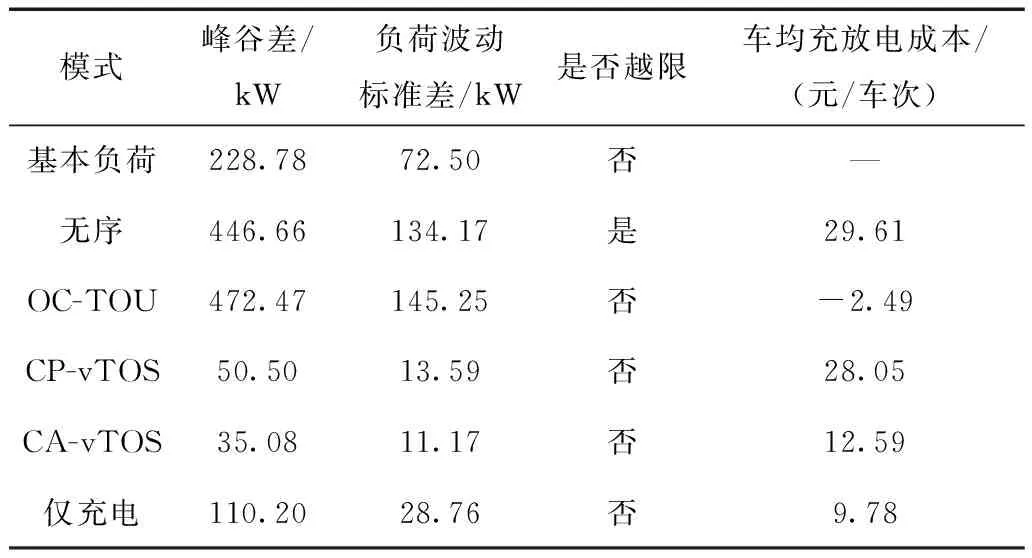
模式峰谷差/kW负荷波动标准差/kW是否越限车均充放电成本/(元/车次)基本负荷228.7872.50否—无序446.66134.17是29.61OC-TOU472.47145.25否-2.49CP-vTOS50.5013.59否28.05CA-vTOS35.0811.17否12.59仅充电110.2028.76否9.78

无序充电模式下，大量电动汽车集中在负荷晚高峰时段充电，进一步加剧了系统峰谷差，最大负荷超过变压器容量限制的10.55%，影响到配电网的安全可靠运行。在OC-TOU优化模式中，车辆仅单纯地倾向于在电价高峰时放电，低谷时充电，对系统负荷起到良好的转移作用，但是，从图4中可以看出，该模式已导致配电网负荷出现“峰谷颠倒”现象，新产生的负荷峰值已经高于基本负荷的峰荷，且负荷波动标准差也超过基本负荷。在CP-vTOS、CA-vTOS充放电优化模式中，车辆在虚拟电价高峰时放电，低谷时充电，对系统负荷起到削峰填谷作用，相比于无序充电，峰谷差、负荷波动率均有所降低。由于CA-vTOS充放电优化模式可以灵活地调节充放电功率，因此在改善负荷波动方面具有更大的优势。仅充电优化模式中，因为不考虑V2G服务，电动汽车集群负荷无法削峰，但具有较好的填谷能力。

为观察具体单用户的收益情况，随机模拟一次电动汽车集群的充电行为，无序与CA-vTOS充放电优化模式下的各电动汽车用户总成本对比如图5所示。

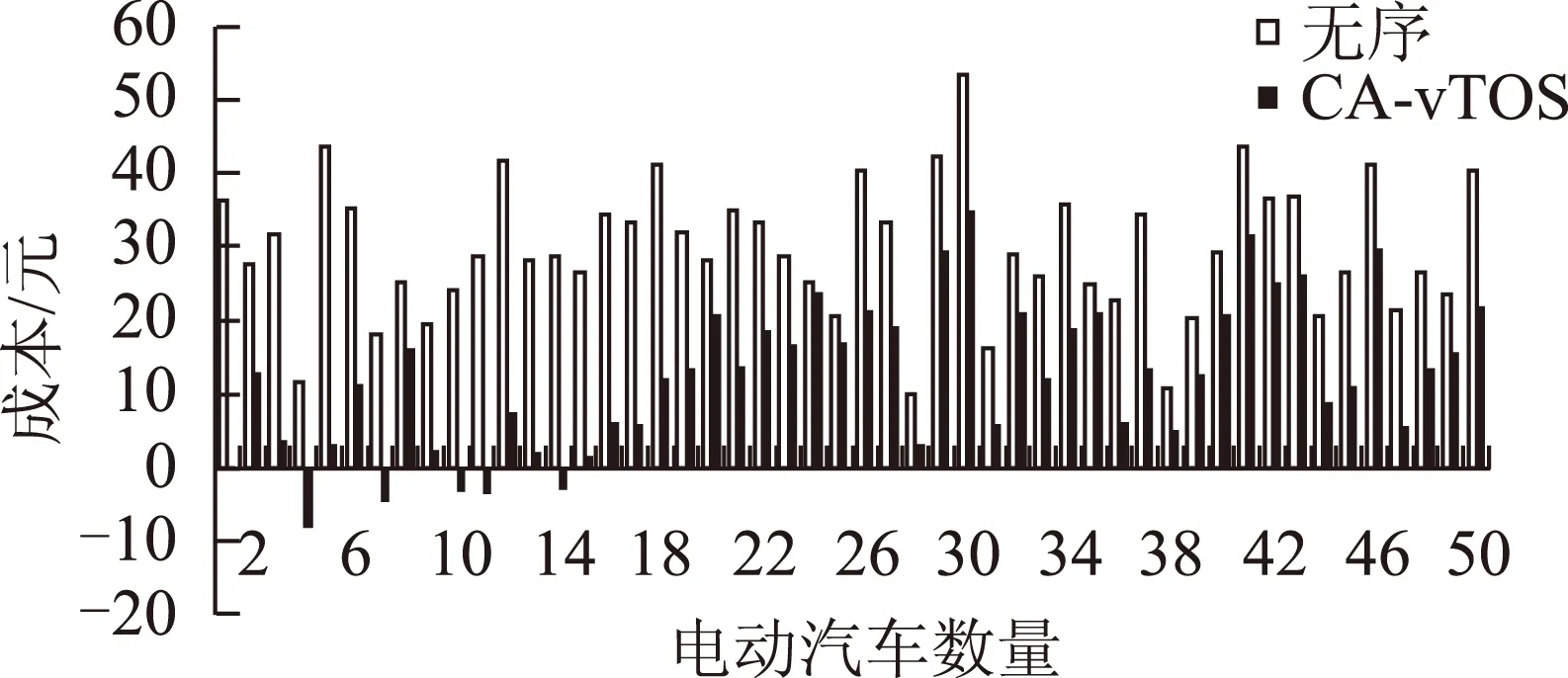
图5　无序与CA-vTOS优化模式下的用户总成本对比Fig.5　Comparison of customer cost under uncoordinated and CA-vTOS methods

仿真结果表明，经CA-vTOS优化后的各用户总成本均低于无序充电，确保了所有用户均有收益。此外，仿真过程中发现，在第20辆车以后，负荷曲线已明显平滑，且电网侧付诸的激励费用会相应降低，这符合电网侧期望。

从表1中的车均充放电成本情况来看，相较于无序充电，其余4种优化模式对用户侧的车均充放电成本也均有所改善。进一步，5种控制模式下，电动汽车集群的电能损失量以及电能损失费用、电池损耗折算成本等的对比如图6所示。

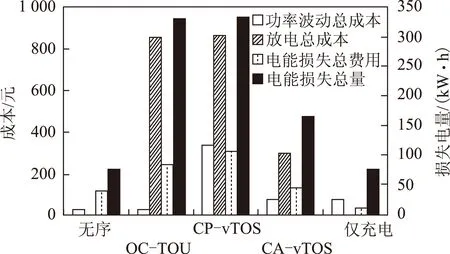
图6　5种控制模式的电能损失、电池损耗折算成本对比Fig.6　Comparison of energy loss cost and battery degradation cost under five control methods

结合图4、图6和表1，OC-TOU模式的收益最优，但其造成的电能损失量较大，违背了节能的消费理念，且其优化后的负荷曲线各参数均不理想，不利于配电网的安全、可靠运行。CP-vTOS、CA-vTOS两种模式下，负荷曲线相近，但CP-vTOS造成的电能损失量较大，对电池的损耗较大，难以得到用户的认可。仅充电模式在电能损失量及电池损耗方面均优于CA-vTOS充放电模式，在用户侧车均充放电成本方面较CA-vTOS模式降低了22.32%，但经过仅充电模式优化后的负荷峰谷差和波动标准差仍较大。

综上，CA-vTOS模式虽然有优越的削峰填谷效果，但用户成本并非最优，因此，用户需要根据激励水平及自身消费心理考虑是否参与V2G服务；另一方面，配电网需要根据削峰填谷的迫切程度、用户响应度对利益反馈力度进行不同强度的管控。

4.4灵敏度分析

1)电动汽车集群规模对优化结果的影响。

图7为不同电动汽车集群规模下，无序和CA-vTOS模式优化后的负荷曲线对比。表2列出了不同规模下，CA-vTOS模式的负荷曲线统计信息。

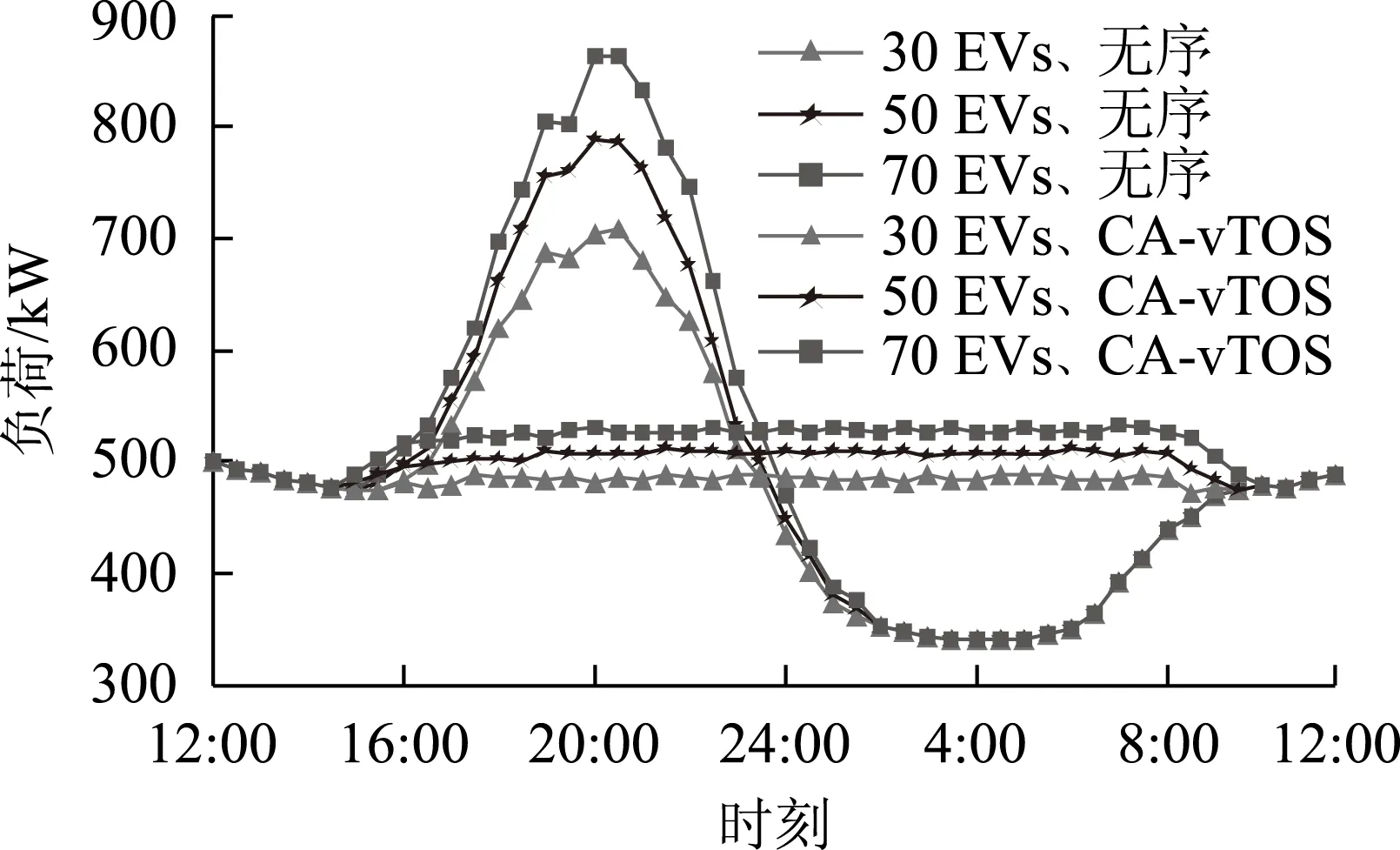
图7　不同电动汽车规模下的负荷曲线对比Fig.7　Load curves with different scales of EVs表2　不同规模下CA-vTOS模式的统计信息Tab.2　Results of CA-vTOS method with different scales of EVs

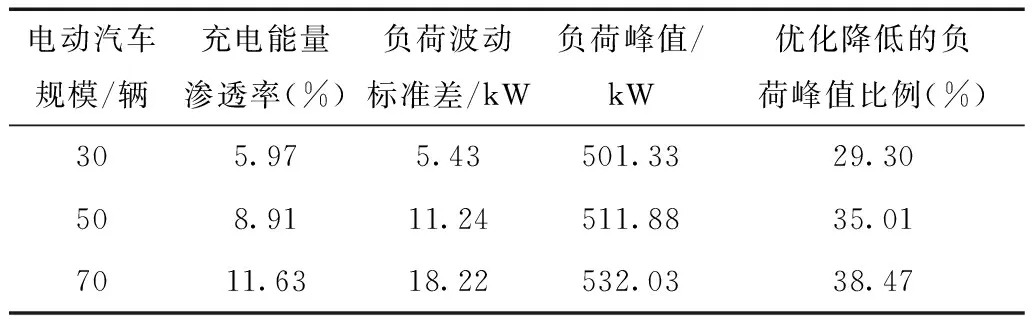
电动汽车规模/辆充电能量渗透率(%)负荷波动标准差/kW负荷峰值/kW优化降低的负荷峰值比例(%)305.975.43501.3329.30508.9111.24511.8835.017011.6318.22532.0338.47

随着充电能量渗透率的增大，负荷波动标准差会增大，说明接入的电动汽车规模较大，已超过该配电网的最佳接入规模，但在车辆的主要停放时段(16∶00～次日8∶00)，优化后的负荷曲线依然很平滑，并不会出现“峰谷颠倒”现象，突出了所提优化方法的优越性。

2)鲁棒性(基本负荷预测误差对结果的影响)。

目前，尚没有出现一种方法能准确地预测未来一段时间的基本负荷值，实际负荷总与预测负荷有一定的不确定出入。因此，该部分讨论基本负荷的预测误差对优化结果的影响。不同预测误差下的配电网总负荷曲线如图8所示。图8中，基本负荷由预测所得，具体预测方法不在本文研究范围内，本文假设基本负荷值可通过历史负荷数据和天气状况预测得到，并设相对预测误差服从[-δ, δ]的均匀分布，则3种特定预测误差下的实际基本负荷可由基本负荷预测值叠加对应预测误差负荷得到。

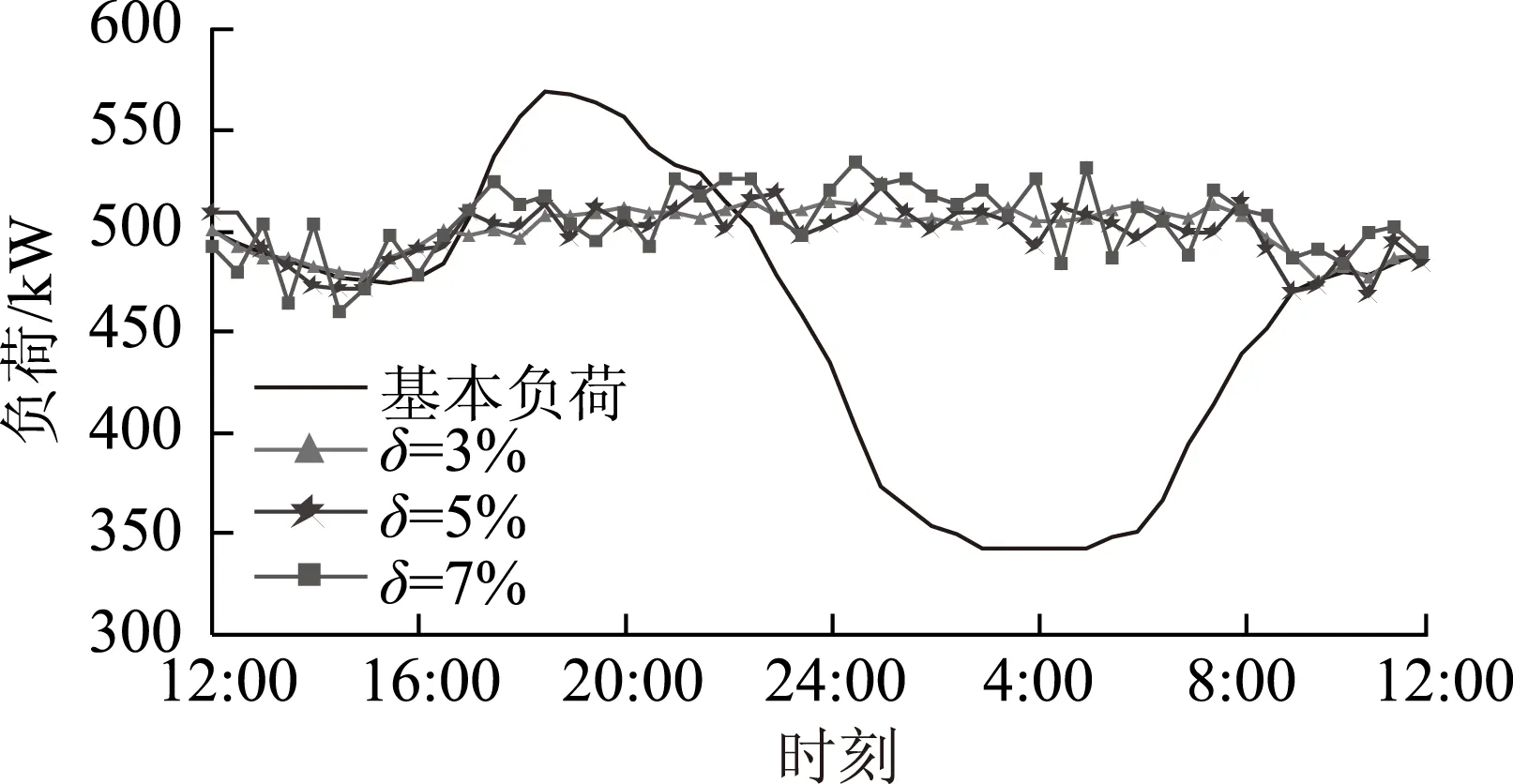
图8　不同基本负荷预测误差下的负荷曲线Fig.8　Load curves with different levels of base load prediction errors

仿真结果表明，即使在预测误差为7%的情况下，削峰填谷效果也非常可观。进一步，3条总负荷曲线的波动标准差分别为11.60、14.18和17.82，对比基本负荷的波动标准差72.50，可以得到结论：基本负荷的预测误差对CA-vTOS模式的优化结果影响不明显。

3)用户响应优化调度的概率对结果的影响。

用户选择响应何种充电模式，还受到用户行为习惯及消费心理的影响，本节采用随机的方式描述用户的响应行为，讨论用户响应调度概率对结果的影响，仿真结果如图9所示。

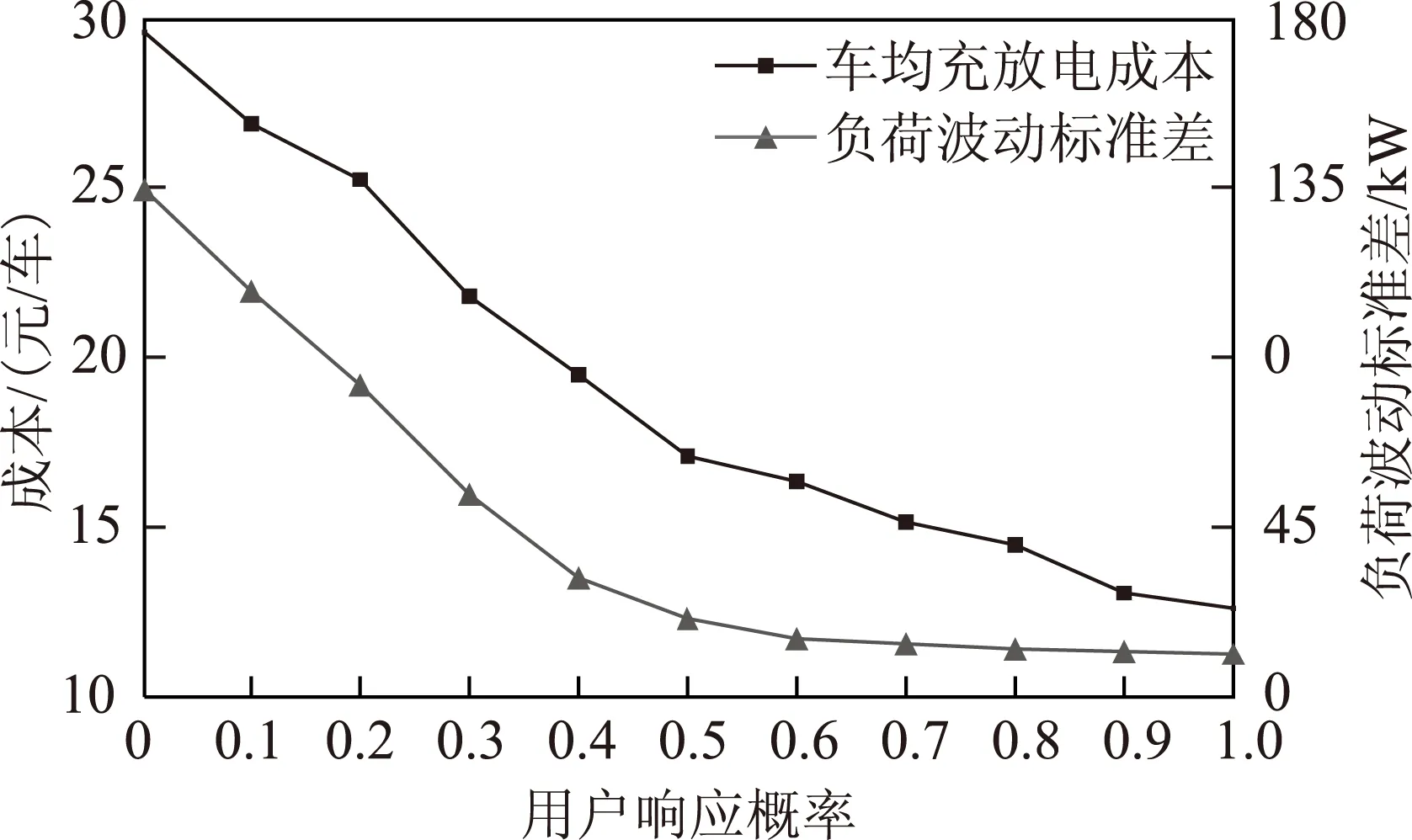
图9　用户响应优化调度的概率对车均充放电成本 和负荷波动标准差的影响Fig.9　Effects of customer response probability in CA-vTOS on average cost per EV and standard deviation

图9显示，用户响应调度的概率越大，用户的车均充放电成本越低，同时削峰填谷效果越显著，实现用户与配电系统的共赢，其主要原因是响应资源的增多，可以使更多的峰时段负荷被消减，并移动至夜间负荷低谷时段，从而进一步降低车均充电成本、平抑系统负荷波动。因此，调度模型的执行效果需要更多地关注用户的响应能力和响应意愿的不确定性。

4)峰谷电价对结果的影响。

在高峰电价确定的前提下，针对CA-vTOS优化模式就不同峰谷电价比例对仿真结果的影响进行研究，结果如图10所示。

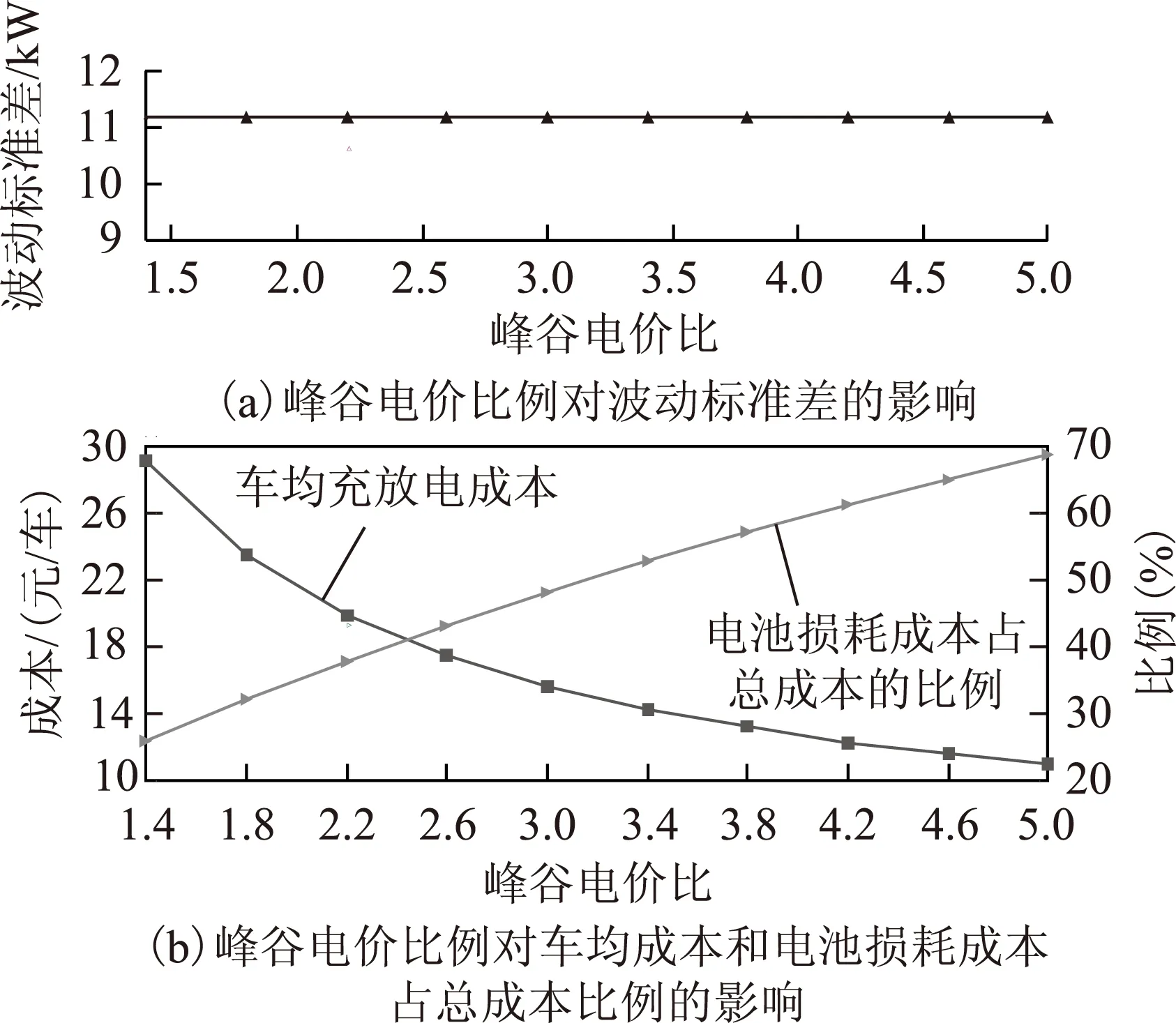
图10　峰谷电价比例对结果的影响Fig.10　Effects of peak/valley price ratio on simulation results

从结果可以看出，峰谷电价比例不会影响负荷波动率，但随着峰谷电价比例的增加，车均成本降低，用户将更有意愿响应充放电调度，另一方面，也意味着供电侧的激励成本将增加。此外，峰谷电价比例的增加会使电池损耗等隐性成本占总成本的比例上升，更加凸显电动汽车集群削峰潜力的挖掘需求与电池技术水平的矛盾。实际操作中，需要综合考虑用户的响应度及电力缺口情况确定合理的电价比例。

5　结论

本文面向局域配电网中常规充电的电动汽车，构建了以削峰填谷为目的、兼顾配电系统负荷信息与用户电能损失费用及电池损耗成本的电动汽车充放电优化调度和实现机制模型。通过仿真分析，得出结论如下。

1)采用所提优化方法，能够在满足用户充电需求及配电变压器容量限制的基础上，实现电动汽车集群负荷的削峰填谷，并降低用户的充放电成本，易于被电动汽车用户接受。

2)采用所提优化方法，在电动汽车集群规模较大时仍可在连接电网时段平滑负荷曲线，避免出现峰谷奇异现象，且此时电网侧付诸的激励费用会相应降低，符合电网侧期望。

3)文中针对5种模式对用户各部分成本进行了详细分析，相比于所列的对比优化模式，功率连续可调的充放电优化模式具有优越的削峰填谷能力，总体性能较好，且具有良好的鲁棒性。但是，在目前动力电池技术水平尚未取得关键突破的情况下，电动汽车参与V2G服务的放电成本在总成本中仍占据较大份额，V2G效用的发挥亟需电池技术的发展。

4)在具体实施动态分时电价机制的过程中，需要综合考虑用户的消费心理、外界因素在执行过程中对用户响应意愿性的影响及实时电力缺口情况来动态调整峰谷电价，提高用户与供电侧的共赢程度。

[1]Cheng Lin，Chang Yao，Wu Qiang，et al.Evaluating charging service reliability for plug-in EVs from the distribution network aspect[J].IEEE Transactions on Sustainable Energy，2014，5(4)：1287-1296.

[2]Yao Weifeng，Zhao Junhua，Wen Fushuan，et al.A hierarchical decomposition approach for coordinated dispatch of plug-in electric vehicles[J].IEEE Transactions on Power Systems，2013，28(3)：2768-2778.

[3]Sexauer J M，Mcbee K D，Bloch K A.Applications of probability model to analyze the effects of electric vehicle chargers on distribution transformers[J].IEEE Transactions on Power Systems，2013，28(2)：847-854.

[4]王锡凡，邵成成，王秀丽，等.电动汽车充电负荷与调度控制策略综述[J].中国电机工程学报，2013，33(1)：1-10.

Wang Xifan，Shao Chengcheng，Wang Xiuli，et al.Survey of electric vehicle charging load and dispatch control strategies[J].Proceedings of the CSEE，2013，33(1)：1-10.

[5]财政部.关于公布电力需求侧管理城市综合试点工作首批试点城市名单的通知[EB/OL].[2012-11-01].http：//jjs.mof.gov.cn/zhengwuxinxi/tongzhigon ggao/201211/t20121101_691456.html.

[6]Raslavicius L，Azzopardi B，Kersys A，et al.Electric vehicles challenges and opportunities：Lithuanian review[J].Renewable and Sustainable Energy Reviews.2015，42：786-800.

[7]Qi Wei，Xu Zhiwei，Shen Z J M，et al.Hierarchical coordinated control of plug-in electric vehicles charging in multifamily dwellings[J].IEEE Transactions on Smart Grid，2014，5(3)：1465-1474.

[8]Leou R C，Su C L，Lu C N.Stochastic analyses of electric vehicle charging impacts on distribution network[J].IEEE Transactions on Power Systems，2014，29(3)：1055-1063.

[9]谭小波，赵海，彭海霞，等.电动汽车准实时协同充放电策略[J].电工技术学报，2015，30(13)：70-76.

Tan Xiaobo，Zhao Hai，Peng Haixia，et al.Quasi-real-time coordinated charging/discharging policy for electric vehicles[J].Transactions of China Electrotechnical Society，2015，30(13)：70-76.

[10]Leemput N，Geth F，Claessens B，et al.A case study of coordinated electric vehicle charging for peak shaving on a low voltage grid[C]//3rd IEEE PES Innovative Smart Grid Technologies Europe，Berlin，Germany，2012：1-7.

[11]Geng B，Mills J K，Sun D.Coordinated charging control of plug-in electric vehicles at a distribution transformer level using the vTOU-DP approach[C]//IEEE Vehicle Power and Propulsion Conference，Seoul，Korea，2012：1469-1474.

[12]Luo Zhuowei，Hu Zechun，Song Yonghua，et al.Optimal coordination of plug-In electric vehicles in power grids with cost-benefit analysis，part Ⅰ：enabling techniques[J].IEEE Transactions on Power Systems，2013，28(4)：3546-3555.

[13]Hoog J D，Alpcan T，Brazil M，et al.Optimal charging of electric vehicles taking distribution network constraints into account[J].IEEE Transactions on Power Systems，2015，30(1)：365-375.

[14]王岱，管晓宏，吴江，等.基于车辆行驶行为特性建模的电动汽车充放电策略与分析[J].电网技术，2014，38(9)：2322-2327.

Wang Dai，Guan Xiaohong，Wu Jiang，et al.Vehicle driving pattern based modeling and analysis of centralized charging/discharging strategy for plug-in electric vehicles[J].Power System Technology，2014，38(9)：2322-2327.

[15]王蓓蓓.面向智能电网的用户需求响应特性和能力研究综述[J].中国电机工程学报，2014，34(22)：3654-3663.

Wang Beibei.Research on consumers’ response characterics and ability under smart grid：a literatures survey[J].Proceedings of the CSEE，2014，34(22)：3654-3663.

[16]孙近文，万云飞，郑培文，等.基于需求侧管理的电动汽车有序充放电策略[J].电工技术学报，2014，29(8)：64-69.

Sun Jinwen，Wan Yunfei，Zheng Peiwen，et al.Coordinated charging and discharging strategy for electric vehicles based on demand side management[J].Transactions of China Electrotechnical Society，2014，29(8)：64-69.

[17]孙晓明，王玮，苏粟，等.基于分时电价的电动汽车有序充电控制策略设计[J].电力系统自动化，2013，37(1)：191-195.

Sun Xiaoming，Wang Wei，Su Su，et al.Coordinated charging strategy for electric vehicles based on time-of- use Price[J].Automation of Electric Power Systems，2013，37(1)：191-195.

[18]徐智威，胡泽春，宋永华，等.基于动态分时电价的电动汽车充电站有序充电策略[J].中国电机工程学报，2014，34(22)：3638-3646.

Xu Zhiwei，Hu Zechun，Song Yonghua，et al.Coordinated charging strategy for PEV charging stations based on dynamic time-of-use tariffs[J].Proceedings of the CSEE，2014，34(22)：3638-3646.

[19]Bahrami S，Parniani M.Game theoretic based charging strategy for plug-in hybrid electric vehicles[J].IEEE Transactions on Smart Grid，2014，5(5)：2368-2375.

[20]黄贵鸿，雷霞，杨毅，等.考虑风电与用户满意度的电动汽车两层智能充放电策略[J].电工技术学报，2015，30(5)：85-97.

Huang Guihong，Lei Xia，Yang Yi，et al.Two-layer smart charge-discharge strategies for electric vehicles considering wind generation and users’ satisfaction[J].Transactions of China Electrotechnical Society，2015，30(5)：85-97.

[21]戴诗容，雷霞，程道卫，等.分散式电动汽车入网策略研究[J].电工技术学报，2014，29(8)：57-63.

Dai Shirong，Lei Xia，Cheng Daowei，et al.Study on V2G strategy of distributed electric vehicles[J].Transactions of China Electrotechnical Society，2014，29(8)：57-63.

[22]Luo Xiao，Xia Shiwei，Chan K W.A decentralized charging control strategy for plug-in electric vehicles to mitigate wind farm intermittency and enhance frequency regulation[J].Journal of Power Sources，2014，248 (7)：604-614.

[23]白杨，谢乐，夏清，等.中国推进售电侧市场化的制度设计与建议[J].电力系统自动化，2015，39(14)：1-7.

Bai Yang，Xie Le，Xia Qing，et al.Institutional design of Chinese retail electricity market reform and related suggestions[J].Automation of Electric Power Systems，2015，39(14)：1-7.

[24]中共中央国务院.中共中央国务院关于进一步深化电力体制改革的若干意见[EB/OL].[2015-03-15].http：//www.chinapower.com.cn/newsarticle/1231/new

1231828.asp.

[25]赵洪山，王莹莹，陈松.需求响应对配电网供电可靠性的影响[J].电力系统自动化，2015，39(17)：49-55.

Zhao Hongshan，Wang Yingying，Chen Song.Impact of demand response on distribution system reliability[J].Automation of Electric Power Systems，2015，39(17)：49-55.

[26]Qian Kejun，Zhou Chengke，Allan M，et al.Modeling of load demand due to EV battery charging in distribution systems[J].IEEE Transactions on Power Systems，2011，26(2)：802-810.

[27]Geng B，Mills J K，Sun D.Two-stage charging strategy for plug-in electric vehicles at the residential transformer level[J].IEEE Transactions on Smart Grid，2013，4(3)：1442-1452.

[28]翁国庆，张有兵，戚军，等.多类型电动汽车电池集群参与微网储能的V2G可用容量评估[J].电工技术学报，2014，29(8)：36-45.

Weng Guoqing，Zhang Youbing，Qi Jun，et al.Evaluation for V2G available capacity of battery groups of electric vehicles as energy storage elements in microgrid[J].Transactions of China Electrotechnical Society，2014，29(8)：36-45.

[29]He Yifeng，Venkatesh B，Guan Ling.Optimal scheduling for charging and discharging of electric vehicles[J].IEEE Transactions on Smart Grid，2012，3(3)：1095-1105.

[30]北京交通研究中心.2011年北京交通发展年度报告[EB/OL].[2013-05-06].http：//www.bjtrc.org.cn/.

Virtual Time-of-Use Tariffs Based Optimal Scheduling and Implementation Mechanism of Electric Vehicles Charging and Discharging

Yang Xiaodong1Zhang Youbing1Weng Guoqing1Zhao Bo2Gao Xiang3

(1.College of Information EngineeringZhejiang University of TechnologyHangzhou310023China 2.State Grid Zhejiang Electric Power Research InstituteHangzhou310014China 3.State Grid Lishui Municipal Electric Power CompanyLishui323000China)

The optimal scheduling of electric vehicles’ (EVs) charging and discharging based on virtual time-of-use (vTOU) tariffs is put forward.By taken the load information of the distribution system，the power loss cost，and the battery consumption cost of customers into consideration，the models of the charging and discharging optimal scheduling and the implementation mechanism are developed for the purpose of peak shaving.In the proposed models，the charging and discharging power is associated with the load information by vTOU tariffs.Then the power adjustment of the EVs is researched based on minimizing the virtual cost.Accordingly，a dynamic time-of-use tariff for EVs’ charging and discharging is established based on the wavelet analysis and the fuzzy cluster to ensure the implementation of the scheduling strategy.Finally，five optimization modes are simulated by charging piles in a residential district.The results illustrate the basic characteristics of the proposed models.

Electric vehicle (EV)，virtual time-of-use tariff，peak shaving，charging and discharging optimization，adjustable power，implementation mechanism

2015-05-31改稿日期2015-12-07

TM 73；U469.72

杨晓东男，1990年生，博士研究生，研究方向为电力系统通信、电动汽车入网、智能用电等。

E-mail：yang_xd90@163.com

张有兵男，1971年生，博士，教授，研究方向为智能电网、分布式发电及新能源优化控制、电动汽车入网、电力系统通信、电能质量监控等。

E-mail：youbingzhang@zjut.edu.cn(通信作者)

国家自然科学基金(51207139，51207140)和浙江省自然科学基金(LY16E070005)资助项目。