基于BP神经网络的分数阶PIαDβ控制器参数整定研究

那景童,徐　驰

(大连交通大学 电气信息学院,辽宁 大连116028)



基于BP神经网络的分数阶PIαDβ控制器参数整定研究

那景童,徐驰

(大连交通大学 电气信息学院,辽宁 大连116028)

对于分数阶控制系统，因分数阶控制器较传统PID控制器具有更好的适应性，这就为得到更加细腻的控制品质提供了可能。然而，分数阶PIαDβ控制器的参数整定则相对复杂。针对这一问题，提出了基于BP神经网络的分数阶控制器参数整定方法，有效地克服了分数阶控制器参数整定复杂问题。采用文章所提方法，分别设计了整数阶PID、分数阶PIαDβ控制器，并进行仿真对比。结果表明，采用分数阶PIαDβ控制器的系统控制品质优于整数阶PID控制器。

分数阶系统；BP神经网络；控制器参数整定；分数阶控制器

分数阶微积分几乎与传统整数阶微积分同时被提出[1]，因此分数阶微积分理论建立至今已有至少300年的历史，然而早期主要侧重于理论研究，直到近年来很多领域才开始应用分数阶微积分理论。在自动控制领域出现了分数阶控制理论这一新颖研究方向[2]，分数阶控制理论较传统控制理论提高了对动态系统的设计、表征和控制的能力，其意义就是对于古典整数阶控制理论的扩展化，它可以建立更准确的模型，得到更鲁棒的控制结果[3]。分数阶控制器参数整定是分数阶控制理论的研究热点问题[4]，但至今还尚未探索出一种合适的分数阶控制器参数整定方法。

目前，基于BP神经网络的PID控制器参数整定方法已经成为一种成熟有效的方法，因此，本文提出了一种基于BP神经网络的分数阶PIαDβ控制器参数整定方法，采用该方法同时对分数阶PIαDβ控制器和整数阶PID控制器进行参数整定，并对控制效果进行比较。

1　分数阶PIαDβ控制器

1.1分数阶微积分理论

到目前为止，分数阶微积分尚无统一定义。在分数阶微积分理论建立过程中出现了由几种函数定义的分数阶微积分定义[5]，如Grunwald-Letnikov(G-L)、 Riemann-Liouville(R-L)、Cauchy、Capotu分数阶微积分定义。本文采用G-L分数阶微积分定义：

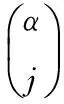
1.2分数阶PIαDβ控制器数学描述

本文所设计的分数阶PIαDβ控制器采用如下形式的数学模型:

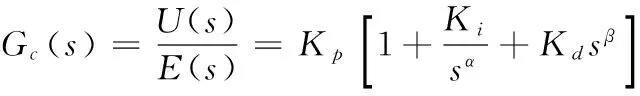
(2)

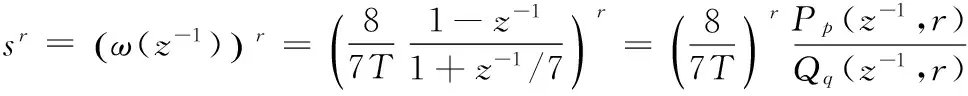
(3)

式中，T为采样周期；r为分数阶微分阶次；P、Q是变量X=(x1,x2,x3,x4)=(e,e-1,ce,ce-1)的多项式，可通过查表得到。采用连分式展开方法，则可得到sr的整数阶传递函数，将所得整数阶传递函数代入到式(2)，即可实现分数阶PIαDβ控制器的离散化。

2　基于BP神经网络的分数阶PIαDβ控制器参数整定

2.1BP神经网络结构确定

BP神经网络[6]结构的确定主要包括输入层、隐层和输出层。输入层输入节点考虑当前时刻和前一时刻的误差和误差变化率，输出层节点数由分数阶PIαDβ控制器可调参数个数决定，而隐层节点个数的选择本文是以尽可能少而又可行为原则，这里选择隐层由5个节点构成，这样神经网络的结构形式即为4-5-5，分数阶控制器的BP神经网络结构如图1。

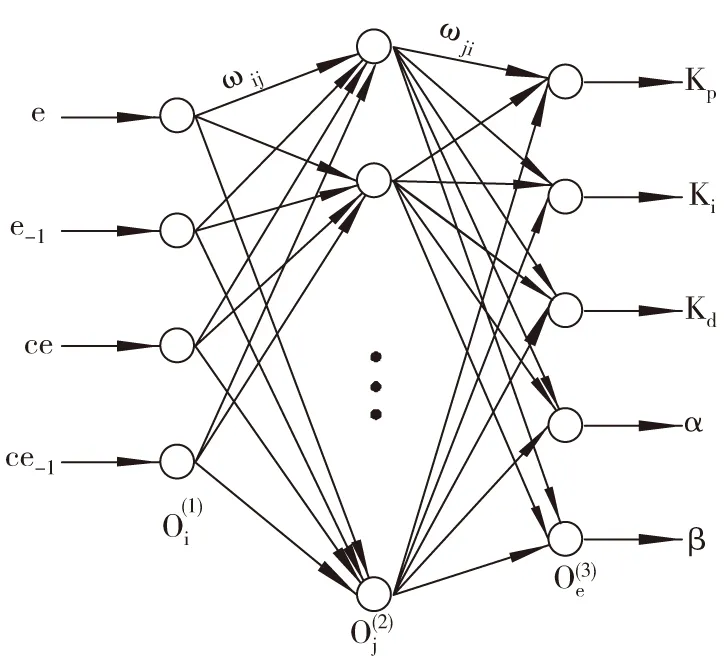
图1　分数阶控制器的BP神经网络结构

2.2基于BP神经网络的分数阶PIαDβ控制器参数整定算法

根据图1所示的BP神经网络结构给出各层输入输出的数学表达式如下：

(1)输入层表达式

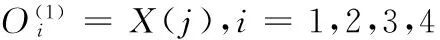
(4)

X=(x1,x2,x3,x4)=(e,e-1,ce,ce-1) 。

(5)

(2)隐层各节点的输入和输出表达式

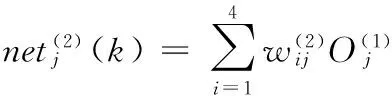
(6)

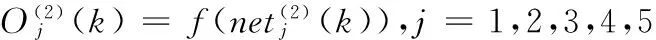
(7)

考虑到Kp,Ki,Kd的值通常为大于或等于零的值，又考虑到0≤α,β≤1，故为了满足输出层5个参数的取值特点，转移函数选择下面的型式：

(8)

(3)输出层各节点的输入和输出表达式为

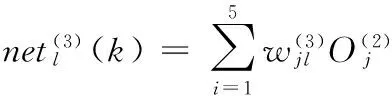
(9)

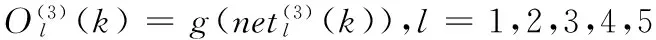
(10)

=(Kp,Ki,Kd,α,β)。

(11)

在推导基于误差反向传播的网络权系数修正算法时，首先选择

(12)

作为误差评价指标公式，然后采用梯度下降法调整神经网络的权系数，当误差进入要求范围内后，则停止权的调整。由输出层误差反传到隐层的权系数调整公式推导如下：

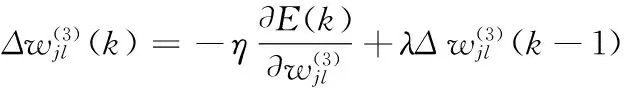
(13)

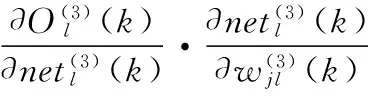
(14)

=-e(k)，

(15)

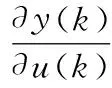
2.3BP神经网络的分数阶PIαDβ控制器

基于BP神经网络的控制器结构图如图2。

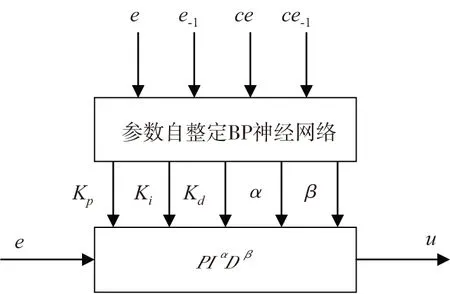
图2　基于BP神经网络的控制器结构图

控制器整定算法步骤如下：

(1)网络初始化。确定各神经网络层的初始权值、动量系数λ及学习率。

(2)BP神经网络训练。利用2.2节相关函数对BP神经网络各层权值进行调节，并计算隐节点输出。

3　算法有效性验证

为了验证本文所提基于BP神经网络的分数阶PIαDβ控制器的控制性能，选用一类高阶惯性系统做为控制对象[7]，即数学模型可描述为：

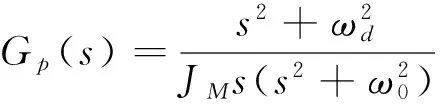
(16)

式中， JM为驱动等效惯量，JM=0.004 kg·m-2；ω0为系统振荡频率，ω0=317.55 rad·s-1；ωd为反振动频率，ωd=226.57 rad·s-1。

利用文章所提分数阶控制器对式(16)控制对象进行控制，本文所选BP神经网络结构为4-5-5，控制器的5个参数整定结果如下：

kp=0.24854，ki=0.1049，kd=0.0011，α=0.1048，β=0.1844。

同时，得到整数阶PID控制器的3个参数为

kp=0.3852，ki=0.1823，kd=0.00076。

(17)

(18)

采用式(17)(18)控制器分别对高阶惯性系统模型(16)进行闭环单位阶跃测试，得到系统仿真对比图,如图3。

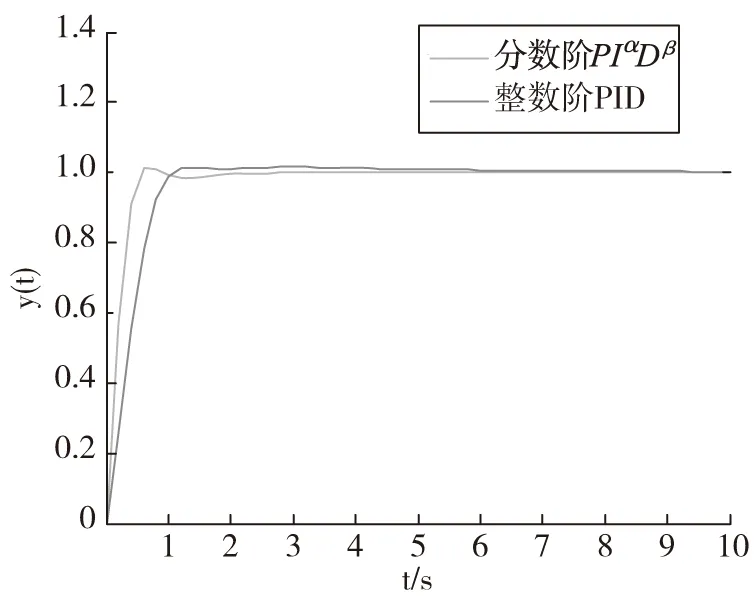
图3　系统单位阶跃对比图

从图3的阶跃响应对比可得，本文设计的分数阶PIαDβ控制器无论是在上升时间、调节时间和超调量均优于整数阶PID控制器。

为了更加直观说明分数阶PIαDβ控制器优越于传统整数阶PID控制器，这里选用两个指标即IAE(绝对误差积分)和TV(输入总变化量)，分别定义为：

IAE=∫0∞e(t)dt；

(19)

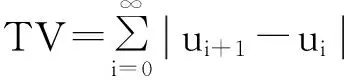
(20)

式中u的采样时间为△t=1s。

两种控制器所对应的IAE和TV见表1。可以看出，相对于传统PID控制器，分数阶PIαDβ控制器具有更小的IAE和TV，而更小的TV意味着对设备伤害更小以及能量消耗更少。

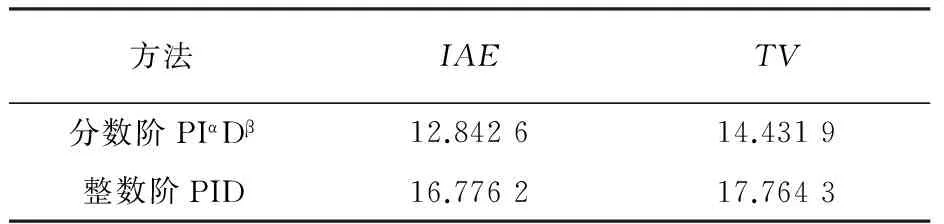
表1　性能指标对比

4　结　论

尽管分数阶PIαDβ控制器与整数阶PID相比，由于增加了两个可调节参数使其具有调节更加灵活、更加细腻、对被控对象具有更广的适应性等优点，但也正是因为这两个可调节参数增加了其参数调节的难度。因此，本文提出的基于BP神经网络的分数阶PIαDβ控制器整定方法具有十分重要的现实意义。将文章所提方法用于一种高阶惯性系统模型上，通过仿真实验结果表明，该方法是行之有效的且优于传统的PID控制器。

[1] PODLUBNY I. Fractional-order systems and PID controllers[J]. IEEE Trans on Automati Control,1999,44(1): 208-214.

[2] 薛定宇. 控制数学问题的MATLAB求解[M]. 北京: 清华大学出版社，2007．

[3] CAPONETTO R. Fractional Order Systems: Modeling and Control Applications[M]. Singapore: World Scientific,2010:1-4.

[4] DAS S, PAN I, DAS S, et al. Improved model reduction and tuning of fractional-order PIλDμcontrollers for analytical rule extraction with genetic programming[J]. ISA Trans, 2012, 51(2): 237-261.

[5] OLDHAM K B, SPANIER J. The fractional calculus[J]. Mathematical Gazette,1974,56(247):396-400.

[6] 魏海坤. 神经网络结构设计的理论与方法[M]．北京: 国防工业出版社，2005．

[7] LI W，HORI Y. Vibration suppression using single neuron-based pi fuzzy controller and fractional-order disturbance observer[J]．IEEE Transactions on Industrial Electronics，2007，54(1) :117-126．

(责任编辑王楠楠)

Research on Fractional Order PIαDβController Tuning based on BP Neural Network

NA Jing-tong, XU Chi

(School of Electrical Information, Dalian Jiaotong University, Dalian Liaoning 116028, China)

Fractional order PIαDβcontroller is more flexible and offers opportunity to obtain better control quality of a fractional order control system than the traditional PID controller. However, the parameters tuning of fractional order controller is more complex. Aming at the problem, a method of fractional order PIαDβcontroller tuning based on BP neural network is presented, which efficiently overcome the complexity of fractional order controller tuning. A fractional order PIαDβcontroller and an integer order PID controller are tuned respectively by using the proposed method. Results show that fractional order PIαDβcontroller can get better performance than integer order PID controller.

fractional order system; BP neural network; controller tuning；fractional order controller

2096-1383(2016)05-0486-03

2016-05-31；最后

2016-07-25

那景童(1989-)，男 ，辽宁大连人，大连交通大学电气信息学院硕士研究生，主要从事分数阶控制研究。

TP273

A