双向地震作用下多层偏心结构的增量动力分析

王　丰，王楠楠，吴　松，吴　林

(大连民族大学 土木工程学院，辽宁 大连116605)



双向地震作用下多层偏心结构的增量动力分析

王丰，王楠楠，吴松，吴林

(大连民族大学 土木工程学院，辽宁 大连116605)

以往的增量动力分析(Incremental Dynamic Analysis, IDA)研究主要是针对单向地震下的对称结构，而对于地震动的多维性、结构偏心引起的扭转效应的影响则考虑较少。为此，设计了一幢5层的偏心结构模型，选取Taft双向地震记录为双向激励对结构模型进行多维增量动力分析。分析了结构在地震下的扭转效应对边缘框架反应的放大作用，并基于IDA能力曲线对结构模型进行多性能水准抗震评估。通过算例分析得到以下结论：基于IDA的结构抗震评估方法，概念清晰，操作简单；偏心结构在双向地震下的扭转效应会导致部分边缘框架的反应放大，且地震强度越大这种放大效应越明显；当考虑双向地震作用时，直接采用建议的双向IDA方法进行结构性能分析更具合理性。

增量动力分析；双向地震动；偏心结构；能力曲线

增量动力分析(Incremental Dynamic Analysis, IDA)方法最早于1977年由Bertero提出，于2000年被美国FEMA350所采用，近年来被应用于结构抗倒塌能力分析和结构性能化抗震设计和评估中。李建中等[1]运用IDA方法对桥梁高墩的屈服位移、极限位移和位移延性能力进行分析，指出高阶振型对桥梁高墩的位移延性有较大影响。一些研究者将IDA和模态Pushover分析相结合，提出了模态IDA方法[2-4]，即运用模态等效单自由度体系替代原结构进行增量动力分析，单独分析后再将各模态结果进行组合，这种简化方法可大大缩短分析时间，且具有一定的准确性。杨成等[5]利用弹塑性反应谱替代弹性反应谱作为IDA方法中的地震强度指标，通过算例分析表明此方法能很好体现结构的非线性反应特征。马千里等[6]利用IDA对Pushover分析的加载模式进行研究，建议应采用多种侧向力模式对结构进行Pushover分析，以全面评价结构不同楼层的抗震性能。卜一和吕西林等[7]采用IDA方法对高层混合结构的性能水准进行研究，给出了控制结构抗震目标的四个性能水准。杨成等[8]分析了地震作用特征对IDA能力曲线的影响，指出IDA能力曲线的差异是由不同地震动的弹塑性谱特征差异以及沿结构高度作用分布特征差异共同构成的。李宁和翟长海等[9]考虑结构偏心对动力反应的影响，将结构等效为平动-扭转的双自由度体系，提出了一种简化的IDA方法，即采用等效双自由度体系替代原结构体系进行增量动力分析。Hossein等[10]采用IDA方法和遗传算法优化技术来估计结构在地震作用下的失效概率，这种方法可大大减少用于失效概率分析的地震记录数量，减少运算工作量，且能获得较准确的结果。Alembagheri等[11]采用IDA方法对混凝土拱坝进行损伤分析，建议了简化的拱坝损伤指标，通过算例表明建议的损伤指标能够正确地反映坝体在不同强度地震作用下的损伤情况。侯炜等[12]采用IDA方法对混凝土核心筒的抗震性能进行评价，并基于IDA方法给出了的核心筒结构的四个性能水准下的层间位移角限值。吕大刚等[13]采用IDA方法对结构进行倒塌分析，提出“折半取中”的原则来确定倒塌极限状态点，通过算例分析指出钢筋屈服后强化特性对结构倒塌能力具有显著影响。

然而，以往关于IDA的研究大多是针对单向地震作用下的对称结构情况，而对于多维地震作用下偏心结构的相关研究较少。研究表明，单向水平地震作用的IDA会高估结构抗震能力及抗倒塌的安全性[14]。而对于偏心结构，当结构的地震反应进入非线性阶段后其反应的不规则性会更加明显[15]。为此，本文对偏心结构进行了双向地震作用下的增量动力分析。首先设计了算例模型，选取了双向地震加速度记录作为结构地震激励，然后分析了扭转效应对边缘框架反应的放大作用，最后基于IDA能力曲线对模型结构进行多性能水准的抗震能力评估。

1　基本原理

1.1IDA原理

IDA方法是对Pushover分析方法的拓展，是近年来发展起来的一种用于评估结构抗震性能的动力参数分析方法。IDA方法的基本过程是：针对一条地震动的加速度乘以一系列比例系数SF以递增式地调整地震动强度参数IM(例如：地面峰值加速度、地面峰值速度、地震烈度、加速度谱Sa (T1,ξ=0.05)等)，从而生成一组具有单调递增强度的地震动记录；针对每一强度的地震动记录对结构进行一次非线性动力时程分析，得到相应的结构性能参数DM(例如：最大层间位移角、结构损伤指数、顶层最大位移等)。类似于Pushover分析的基底剪力-顶层位移能力曲线，将地震动的强度参数IM与其对应的结构性能参数DM画入同一坐标系下，其中IM为纵坐标，DM为横坐标，可形成DM-IM格式的IDA能力曲线。通过IDA能力曲线，可以直观地确定结构的地震需求，还可以观察到随着地震动强度的逐渐增强结构所体现出的性能变化特征，进而评估结构的抗震能力。

仅通过一条地震动建立IDA能力曲线不具有统计性，不能反映特定场地的地震动特征和结构地震需求，所以通常情况下IDA方法采用多条地震动进行分析，分别建立IDA能力曲线。假定每条IDA能力曲线均服从正态分布，在某一DM值下得到不同IM值的均值μ和对数值的标准差δ，进而得到(DM,μ)、(DM,μ×e+δ) 和 (DM,μ×e-δ) 三条分位曲线，对应的概率值分别为50 %、84 %和16 %，其中50 %对应均值能力曲线，84 %和16 %对应的能力曲线反映不同地震动分析结果的离散程度。

1.2参数选择

抗震设计规范给出了对应不同设防烈度下小震和大震的地面峰值加速度(Peak Ground Acceleration, PGA)，以及小震和大震下的结构弹性和弹塑性层间位移角限值，所以建议在IDA分析中采用PGA作为地震动强度参数，最大层间位移角作为结构性能参数。

根据规范以及以往研究成果，给出多层钢筋混凝土框架结构在不同抗震性能水准下的最大层间位移角区间，见表1。本文算例即参考此表中参数进行多性能水准的结构抗震能力评估。

表1　不同性能水准下的最大层间位移角区间

2　算例分析

2.1结构模型

设计一幢5层的质量偏心的钢筋混凝土框架结构，平面及立面尺寸如图1。图1中边缘框架分别为x1榀框架、x4榀框架、y1榀框架和y4榀框架；CS为各楼层刚心，CM为各楼层质心，质心偏离刚心的偏心距沿x和y方向均为2 m。假设结构各楼层的质心、刚心位置均相同。梁、板混凝土强度等级为C25，柱混凝土强度等级为C30。梁、柱主筋均采用HRB335，箍筋采用HPB235。梁截面均为250 mm×500 mm，梁主筋配筋率约为1.69 %；柱截面均为600 mm×600 mm，柱主筋配筋率约为2.5 %。屋面恒载为6.5 kN·m-2、活载为2.0 kN·m-2；楼面恒载为4.4 kN·m-2、活载为2.0 kN·m-2。设防烈度为8度，II类场地。双向地震加速度分别沿x向和y向(结构主轴方向)作用于每楼层的质心CM点上。

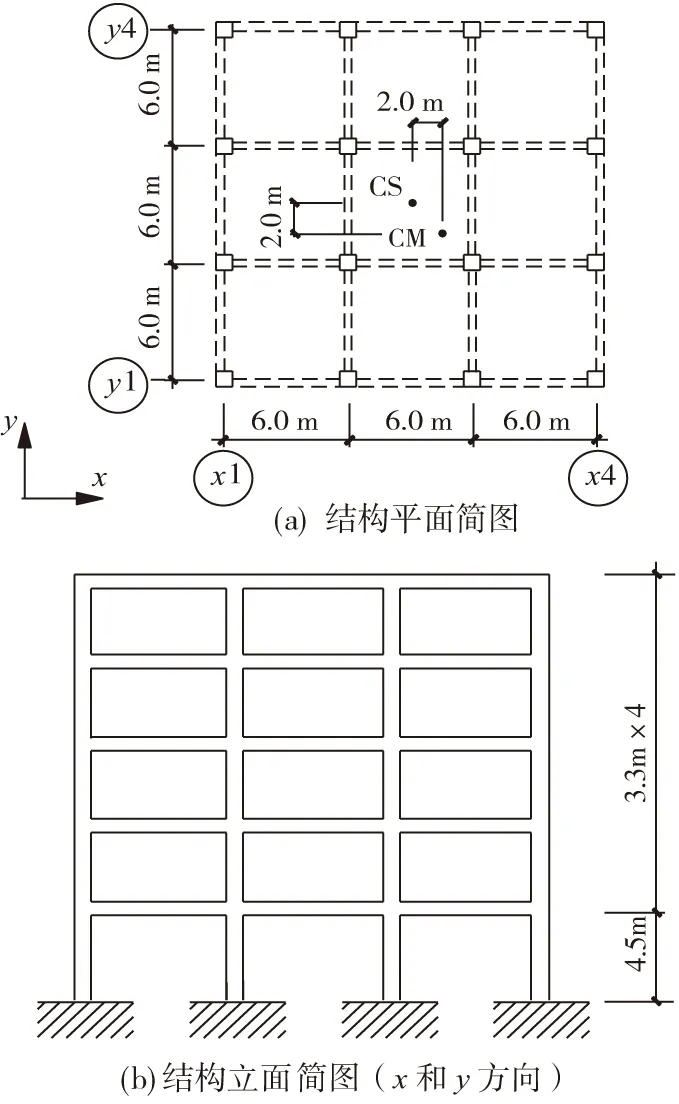
图1　算例结构模型简图

2.2数值分析模型

本算例采用杆系模型进行增量动力分析。设楼板和屋面板均为刚性板，平面内不发生变形，各楼层质量集中在楼板(或屋面板)的质心处。考虑抗震设计中的强节点原则，假设梁柱节点在动力反应中始终处于弹性状态，不发生屈服。梁端设置弯曲塑性铰，恢复力模型假设为双线性刚度退化模型，屈服刚度系数取0.03，刚度退化系数取0.4。梁端屈服弯矩通过配筋梁截面计算得到。柱端采用纤维模型，钢筋纤维和混凝土纤维的材料属性按规范确定。在梁和柱的构件中设置抗剪切弹簧(梁为单向弹簧，柱为双向弹簧)，抗剪承载力通过规范方法计算。由于剪切破坏为脆性破坏，所以在设置力-位移关系时，当达到剪切承载力后抗剪刚度迅速衰减。在梁、柱构件的各种承载力计算中，材料强度均取标准值。构件的刚度系数可通过截面尺寸计算得到。另外，在非线性动力分析之前还需计算出梁、柱构件的初始荷载(包括梁、柱端的初始弯矩、柱的初始轴力、梁的初始剪力等)，并在动力分析前施加在各构件上。

2.3地震记录选取及数据处理

本文选择Taft(Kern County 1952, 1095 Taft Lincoln School)的两水平分量的地震加速度记录进行结构增量动力分析，两个分量的原始加速度时程如图2。

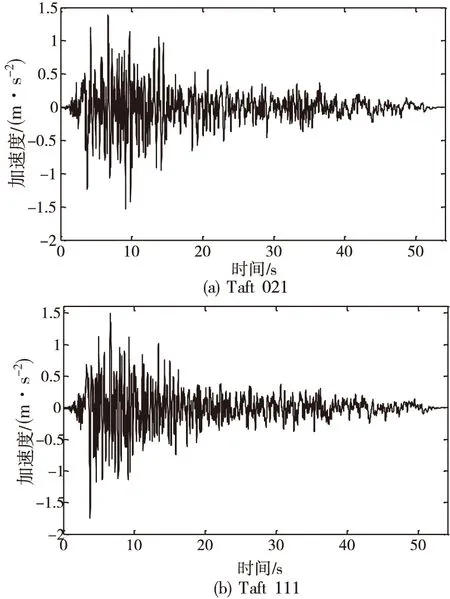
图2　选用的Taft两分量地震加速度记录

目前，在双向地震作用下的结构平-扭耦联动力分析中，针对两分量地震动的幅值关系通常有以下几种处理方式：(1) 由地震记录统计，近似确定两正交分量的峰值加速度比值，然后对两分量的相对加速度进行调幅；(2) 根据规范，设定两分量峰值加速度比值为1∶0.85或0.85∶1，然后对两分量加速度进行调幅；(3) 直接采用各分量地震动记录的峰值加速度，不进行调幅。本文采用了第3种方式，考虑原因如下：本文选取的双分量地震加速度来自于实际地震动记录。任一地震动记录的两个正交水平分量之前的相对强度关系反映了该地震动的特征。

2.4双向地震作用下的IDA能力曲线分析

将Taft地震加速度记录的Taft021分量和Taft111分量分别沿结构的x方向和y方向作用于各楼层的质心。设双向地震加速度的PGA为两个分量PGA的最大值，即PGA=max(PGAx, PGAy)，于是将PGA 调幅为0.1 g等间隔单调递增，得到的地震强度系数IM分别为：0,0.05 g，0.1 g，0.2 g，0.3 g，0.4 g，0.5 g，0.6 g，0.7 g，0.8 g，0.9 g，1.0 g，1.1 g，1.2 g。

PGA为0.05 g和0.6 g时的顶层位移时程曲线如图3，分别对应着小震和大震。由图3可知，随着地震动强度的增加，结构的塑性发展不断加深，且结构基本振动周期也明显增大。

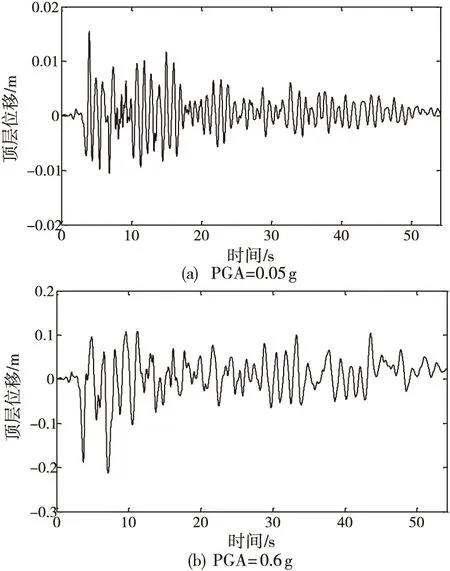
图3　不同强度地震动下的顶层位移时程分析结果 (结构y方向)

地震作用下结构的顶层位移是结构各楼层位移反应的叠加，所以其反映了结构在地震作用下的整体抗震性能。另外，由于等效单自由度体系假设在性能化抗震设计研究中被广泛应用，例如Pushover分析方法、非线性反应谱相关方法等，而该假设中需将结构顶层位移与等效单自由度体系位移建立联系，为此有学者将最大顶层位移作为结构的抗震性能指标进行研究。结构x、y两个方向的最大顶层位移-PGA格式的IDA能力曲线如图4。由于算例模型为质量偏心结构，考虑扭转效应会放大边缘框架的反应，所以图4中分别给出顶层质心、各边缘框架的顶层最大位移增量曲线。由图4可知，大多情况下，边缘框架的最大顶层位移都大于顶层质心处的最大位移，这一特点在强震阶段更为明显，且随着地震强度的增加而增加。

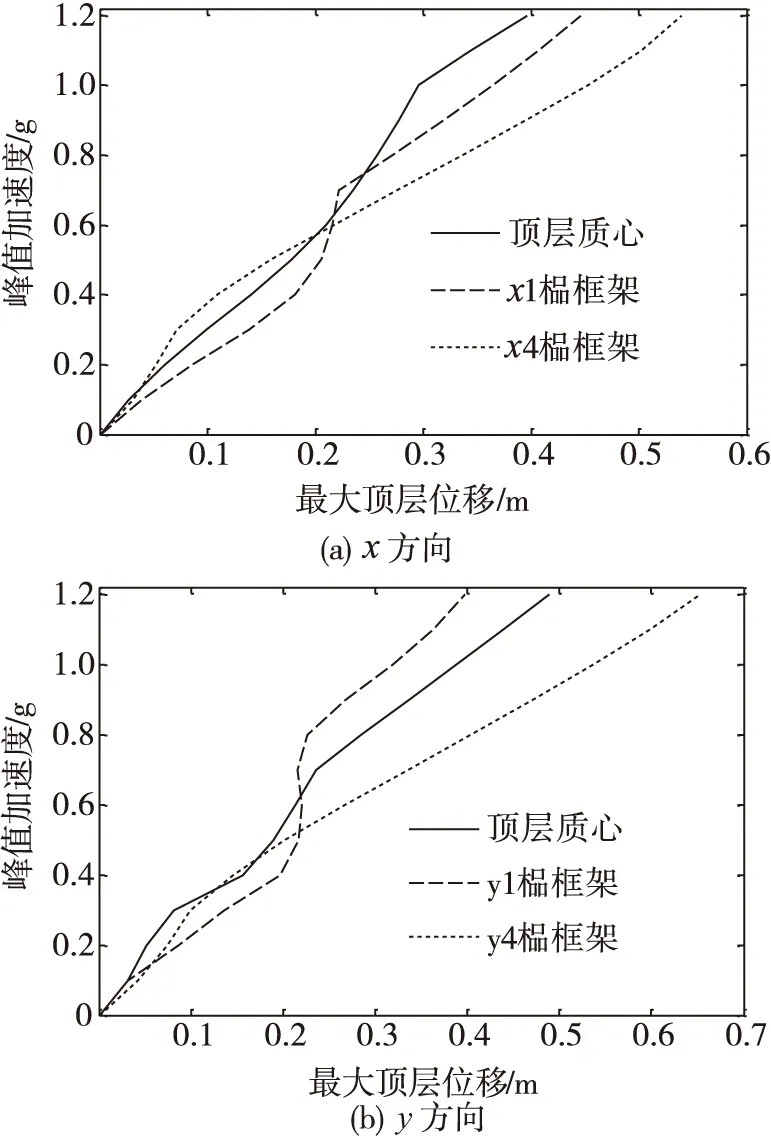
图4　最大顶层位移-PGA格式的IDA能力曲线

尽管最大顶层位移可反映结构的整体震损状态，但由于结构各楼层的反应不可能均衡，最大反应会集中在某个或某几个楼层，所以通过最大顶层位移评估结构抗震性能具有局限性。目前的常用方法是以最大层间位移角或最大楼层位移为指标进行抗震性能评估或抗震验算。结构x、y两个方向的最大层间位移角-PGA格式的IDA能力曲线如图5。为了考虑扭转效应对边缘框架反应的影响，图5中给出了质心处和边缘框架的不同IDA能力曲线。与最大顶层位移的IDA能力曲线不同，图5中的最大层间位移角并不是针对同一楼层，而是取5层中各层最大层间位移角的最大值。与图4的结果相似，在图5中部分边缘框架的最大层间位移角大于质心处的结果，在强震情况下这种现象会更加明显。所以，在抗震设计时对偏心结构的边缘框架应适当增加构件截面及配筋。现有规范已给出了相应的方法，但直接基于反应(位移、层间位移角等)的，且更符合性能化抗震设计理念的边缘框架修正设计方法还有待研究。

图5　最大层间位移角-PGA格式的IDA能力曲线

2.5基于IDA能力曲线的结构多性能水准抗震评估

根据表1中建议的不同性能水准下的最大层间位移角区间，以及规范中给出的小震、中震和大震对应的峰值加速度值，这里通过IDA能力曲线对模型结构进行多性能水准抗震评估，如图6。本算例结构为8度设防，中震加速度取0.2 g，对应的小震和大震峰值加速度分别近似为0.07 g和0.41 g。将不同性能水准的最大层间位移角区间和PGA画入图中，分析得到：(1)x方向，小震下最大层间位移角基本等于1/550；中震和大震下的最大层间位移角均在设定的性能水准区间内，满足要求。(2)y方向，小震下质心和x1榀框架的最大层间位移小于1/550，但x4榀框架的最大层间位移角略大于1/550，超出了限制区间；中震和大震下的最大层间位移角均在设定的性能水准区间内，满足要求。综上分析，应适当提高该模型结构的抗侧刚度，特别是x4榀框架，以减少小震下的侧向变形。

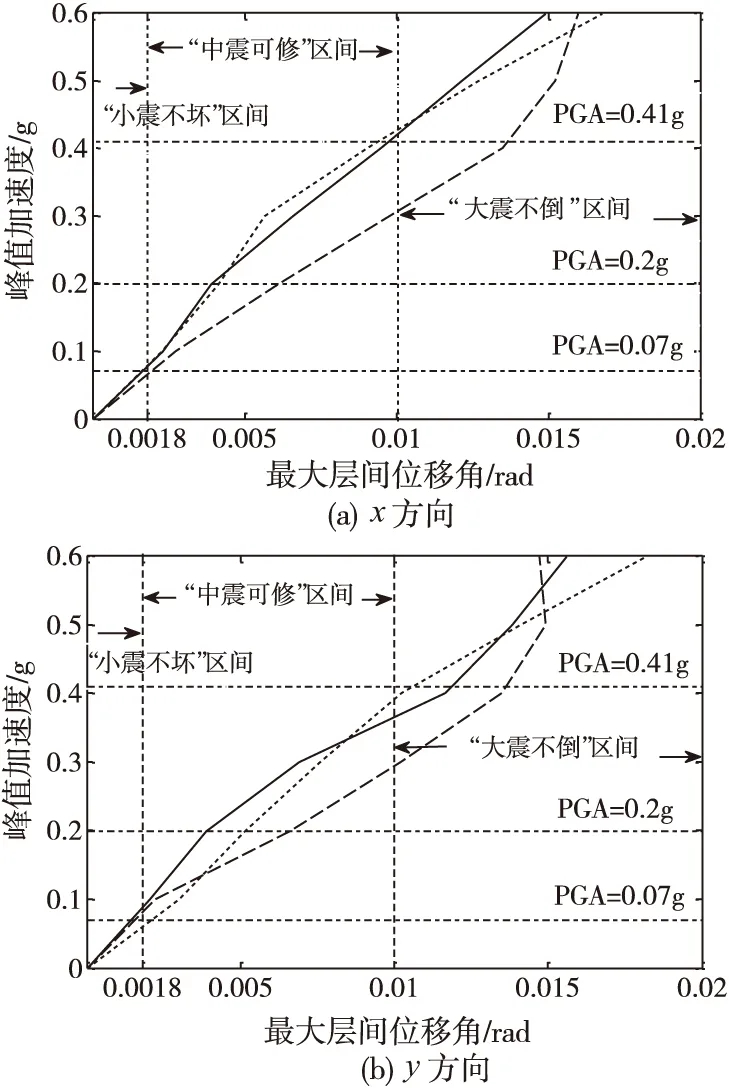
图6　基于IDA能力曲线的结构多性能水准抗震评估

3　结　论

本文针对双向地震作用下结构的IDA进行研究，设计了一幢5层偏心钢筋混凝土框架结构，选取Taft双向地震加速度记录对结构模型进行增量动力分析。以PGA为地震强度参数，分别以最大顶层位移和最大层间位移角为结构性能参数，绘制了两种格式的IDA能力曲线。通过算例分析得到以下结论：

(1) 通过IDA能力曲线对结构进行多性能水准的抗震评估，概念清晰，操作简单，可作为结构的抗震设计验算或抗震性能评估方法使用。

(2) 在双向地震作用下，偏心结构的扭转效应会导致部分边缘框架的动力反应放大，随着地震强度的增大及结构塑性反应的增加，这种放大作用会有所增大。

(3) 相比单向地震作用的IDA方法，双向地震作用的IDA方法可直接进行分析，不需沿两主轴方向分别计算再将反应结果进行组合，因而操作更为简单；另外，其动力分析中直接考虑了双向

平动分量与扭转分量的弹塑性耦合反应，而单向分析方法的动力分析只考虑一个平动分量与扭转分量的耦合反应，所以直接采用双向地震作用进行增量动力分析更具合理性。

[1] 李建中, 宋晓东, 范立础. 桥梁高墩位移延性能力的探讨[J]. 地震工程及工程振动, 2005(1):43-48.

[2] HAN S W, CHOPRA A K. Approximate incremental dynamic analysis using the modal pushover analysis procedure[J]. Earthquake Engineering and Structural Dynamics, 2006, 35(15): 1853-1873.

[3] MOON K H, HAN S W, LEE T S, et al. Approximate MPA-based method for performing incremental dynamic analysis[J]. Nonlinear Dynamics, 2012, 67(4): 2865-2888.

[4] ZARFAM P, MOFID M. On the modal incremental dynamic analysis of reinforced concrete structures, using a trilinear idealization model[J]. Engineering Structures, 2011, 33(4): 1117-1122.

[5] 杨成, 徐腾飞, 李英民,等. 应用弹塑性反应谱对 IDA 方法的改进研究[J]. 地震工程与工程振动, 2008, 28(4): 64-69.

[6] 马千里, 叶列平, 陆新征, 等. 采用逐步增量弹塑性时程方法对RC 框架结构推覆分析侧力模式的研究[J]. 建筑结构学报, 2008, 29(2): 132-140.

[7] 卜一,吕西林.采用增量动力分析方法确定高层混合结构的性能水准[J].结构工程师, 2009,25(2):77-84.

[8] 杨成, 赵世春, 赵人达，等. 地震作用特征对结构IDA曲线的影响分析[J]. 四川大学学报(工程科学版), 2010,42(2): 93-99.

[9] 李宁, 翟长海, 谢礼立. 单向偏心结构的简化增量动力分析方法[J]. 工程力学, 2011 (5): 8-12.

[10] HOSSEIN K, ALIREZA A, MOHSEN G A. Estimating the annual probability of failure using improved progressive incremental dynamic analysis of structural[J]. Structural Design of Tall and Spectral Buildings, 2013, 22(17): 1279-1295.

[11] ALEMBAGHERI M, GHAEMIAN M. Damage assessment of a concrete arch dam through nonlinear incremental dynamic analysis[J]. Soil Dynamics and Earthquake Engineering, 2013,44:127-137.

[12] 侯炜.基于增量动力分析的钢筋混凝土核心筒抗震性能分析与评估[J].世界地震工程,2013, 29(3):121-127.

[13] 吕大刚,于晓辉,王光远. 单地震动记录随机增量动力分析[J].工程力学, 2010 (1): 53-58.

[14] 陆新征, 施炜, 张万开，等. 三维地震动输入对IDA倒塌易损性分析的影响[J]. 工程抗震与加固改造, 2011, 33(6): 1-7.

[15] LUCCHINI A, MONTI G, KUNNATH S. Seismic behavior of single-story asymmetric-plan buildings under uniaxial excitation[J]. Earthquake Engineering and Structural Dynamics, 2009, 38(9): 1053-1070.

(责任编辑邹永红)

Incremental Dynamic Analysis for Multi-storey Asymmetric Structures Subjected to Bi-directional Earthquake Motions

WANG Feng, WANG Nan-nan, WU Song, WU Lin

(School of Civil Engineering, Dalian Minzu University, Dalian Liaoning 116605, China)

The previous researches about incremental dynamic analysis (IDA) focused on the single directional earthquake motions and symmetric structures, and the influences of multi-dimensional earthquake motions and structural eccentricities were not considered. So, a 5-storey asymmetric building is designed, and the Taft bi-directional earthquake records are selected as the earthquake excitations of the example building for the multi-dimensional IDA. The amplification effect of torsion on the responses of edge frames of this example building subjected to the bi-directional earthquake motions is analyzed，and the seismic ability of multi-performance levels of this example building is evaluated based on the IDA capacity curves. The analysis results of the example indicate the following: The seismic evaluation method based on IDA has clear concept and is easy to operate. The torsion effect can induce the amplification of responses of partial edge members of asymmetric structures, and this character is more obvious with the increase of earthquake intensity.For the situation of structures subjected to bidirectional earthquake motions, it is more reasonable to use the bidirectional IDA method for analyzing structural seismic performance.

incremental dynamic analysis; bi-directional earthquake motions; asymmetric structure; capacity curve

2096-1383(2016)05-0496-05

2016-08-02；最后

2016-08-08

国家自然科学基金资助项目(51478091)；辽宁省自然科学基金资助项目(201602198)；辽宁省高等学校优秀人才支持计划资助(LJQ2014139)；中央高校基本科研业务费专项资金资助项目(DC201502040301)。

王丰(1976-)，男，回族，辽宁沈阳人，副教授，博士，主要从事防灾减灾工程研究。

P315.9; TU311.3

A