元素最小描述并集下的多粒度覆盖粗糙集模型

刘财辉，蔡克参

(赣南师范大学 数学与计算机科学学院，江西 赣州 341000)



元素最小描述并集下的多粒度覆盖粗糙集模型

刘财辉，蔡克参

(赣南师范大学 数学与计算机科学学院，江西 赣州 341000)

为了拓展多粒度粗糙集理论在覆盖近似空间上的研究，本文利用元素的最小描述并集并结合条件概率，提出了3种多粒度覆盖粗糙集模型。在模型定义基础上，本文研究了3种新模型的一些特有性质，探讨了新模型与一些已有模型的内在联系与区别，对3种新模型进行了比较。研究结果表明一些已有模型是本文模型的特殊形式，是已有模型的有效拓展。

粗糙集；多粒度；条件概率；覆盖； 最小描述

中文引用格式：刘财辉，蔡克参. 元素最小描述并集下的多粒度覆盖粗糙集模型[J]. 智能系统学报， 2016, 11(4): 534-538.

英文引用格式：LIU Caihui， CAI Kecan. Multigranulation covering rough sets based on the union of minimal descriptions of elements[J]. CAAI Transactions on Intelligent Systems, 2016, 11(4): 534-538.

从解决实际问题的需要，Qian等[1]根据“求同存异”和“求同排异”两种策略，提出了多粒度粗糙集模型，为粗糙集的理论研究开辟了一个全新领域。多粒度粗糙集模型的研究[2-11]引起了人们广泛的关注，例如，通过将三支决策思想[13]引入多粒度粗糙集，Qian等[2]提出了多粒度决策粗糙集模型的概念，并研究了它与已有模型的关系，指出多粒度决策粗糙集模型是一个更一般的模型；Li等[4]研究比较了多粒度粗糙集模型和概念格理论在规则提取中的异同，为多粒度粗糙集的研究提出了新的拓展方向; Yang等[5]研究了多粒度粗糙集模型中的代价敏感问题，为多粒度粗糙集在实际中的应用提供了新思路；Xu等[6]双量化多粒度决策粗糙集模型，较好地推动了多粒度粗糙集模型的应用；She等[7]对多粒度粗糙集模型的代数结构进行了深入探索，给出了一些有指导意义的结论；Huang等[8]对模糊近似空间下的多粒度粗糙集模型进行了深入研究；Lin等[9]利用高斯核，研究了模糊信息系统下的模糊多粒度决策粗糙集模型；Liu等[10]从粒的视角，研究了覆盖近似空间下的多粒度粗糙集模型等。

1　经典多粒度粗糙集的基本概念

定义1[12]给定覆盖近似空间U,C,U是论域,C是U的一个覆盖。对任意的x∈U,称(∀S∈C∧x∈S∧x∈S∧S⊆K⟹K=S)}为x的最小描述。

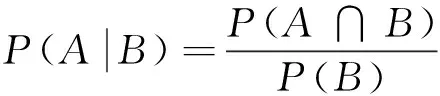
定义3[1]给定K=(U,R),其中R是等价关系簇。 对任意给定的P,Q∈R 和X⊆U, 则X关于P和Q的乐观多粒度下近似和上近似定义如下：

式中～X表示X在U上的补集。

定义4[1]给定K=(U,R),其中R是U上等价关系簇。对任意给定的P,Q∈R 和X⊆U, 则X关于P和Q的悲观多粒度下近似和上近似定义为

为了后续工作的方便，先给出以下2个定义。

2　基于最小描述并集的多粒度覆盖粗糙集及性质

本节利用元素最小描述并集，给出了3种多粒度覆盖粗糙集，对模型的性质进行了深入分析和研究，并探讨了3种模型在α、β变化条件下的演化。

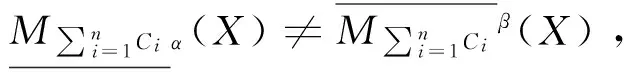
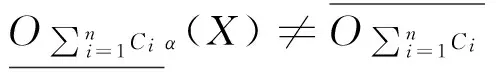
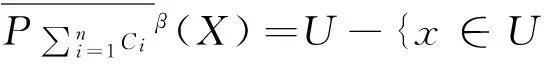
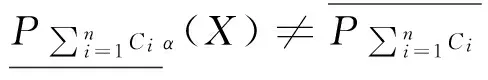
下面给出一个算例对以上定义进行解释说明。

若X={1,2,5,8}，则

对于C1：

对于C2：

若设α=2/3，β=1/2则有

{1,2,3,4,7,8}

下面讨论3种模型的一些基本性质。

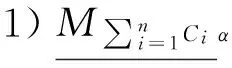
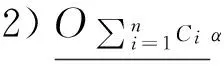
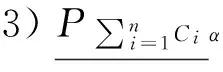
1)当α=1时，有

2)当β=0时，有

证明限于篇幅证明略。

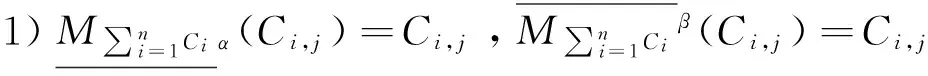
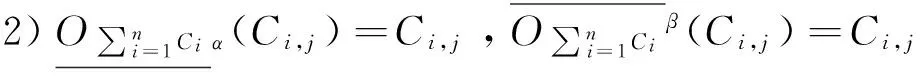
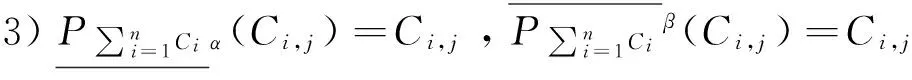
mdC1(1)={{1,2}},mdC1(2)={{1,2},{2,3,4}}mdC1(3)=mdC1(4)={{3,4}}mdC2(1)={{1,3}{1,2,4}}mdC2(3)={{1,3}}mdC2(2)=mdC2(4)={{2,4}}设X={1,2},α=0.6，β=0.3, 则有

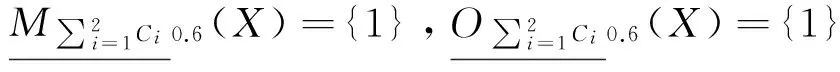
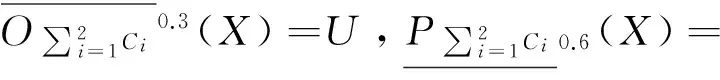
显然有

证明略。

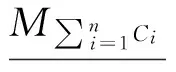
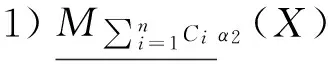
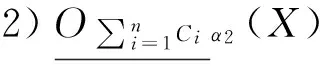
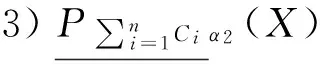
证明略。

定理5告诉我们，在α、β变化的情况下，针对同一目标概念X，使用相同算子进行近似，所得结果是不一样的。α取值越大，相应下近似集反而越小；而β取值越大，相应上近似集越大。

3　3种模型的关系

这小一节讨论了3种新模型之间的内在联系和区别。

证明略。

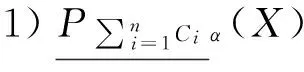
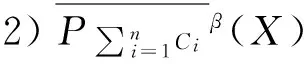
证明略。

4　结论

当前，多粒度粗糙集的理论和应用研究已深受广泛关注。本文在覆盖近似空间下，首先基于元素的最小描述并集并结合条件概率，提出了平均多粒度覆盖粗糙集，乐观多粒度覆盖粗糙集和悲观多粒度覆盖粗糙集，3种多粒度覆盖粗糙集模型。其次，深入研究了3种模型的特有性质，探索了3种模型与经典多粒度粗糙集以及已有2种多粒度覆盖粗糙集模型之间的内在联系与区别，并指出本文所给模型是经典模型在覆盖近似空间上的有效扩展。最后，探讨了三种新模型之间的关系。指出当时，平均多粒度覆盖粗糙下近似和悲观多粒度覆盖粗糙下近似相等；时，平均多粒度覆盖粗糙上近似和乐观多粒度覆盖粗糙上近似相等。发现悲观多粒度覆盖粗糙集和乐观多粒度覆盖粗糙集之间具有包含关系。

[1]QIAN Yuhau, LIANG Jiye, YAO Yiyu, et al. MGRS: a multi-granulation rough set[J]. Information sciences, 2010, 180(6): 949-970.

[2]QIAN Yuhua, ZHANG Hu, SANG Yanli, et al. Multigranulation decision-theoretic rough sets[J]. International journal of approximate reasoning, 2014, 55(1): 225-237.

[3]QIAN Yuhua, LI Shunyong, LIANG Jiye, et al. Pessimistic rough set based decisions: a multigranulation fusion strategy[J]. Information sciences, 2014, 264: 196-210.

[4]LI Jinhai, REN Yue, MEI Changlin, et al. A comparative study of multigranulation rough sets and concept lattices via rule acquisition[J]. Knowledge-based systems, 2016, 91: 152-164.

[5]YANG Xibei, QI Yunsong, SONG Xiaoning, et al. Test cost sensitive multigranulation rough set: model and minimal cost selection[J]. Information sciences, 2013, 250: 184-199.

[6]XU Weihua, GUO Yanting. Generalized multigranulation double-quantitative decision-theoretic rough set[J]. Knowledge-based systems, 2016, 105: 190-205.

[7]SHE Yanhong, HE Xiaoli. On the structure of the multigranulation rough set model[J]. Knowledge-based systems, 2012, 36: 81-92.

[8]HUANG Bing, GUO Chunxiang, ZHUANG Yuliang, et al. Intuitionistic fuzzy multigranulation rough sets[J]. Information sciences, 2014, 277: 299-320.

[9]LIN Guoping, LIANG Jiye, QIAN Yuhua, et al. A fuzzy multigranulation decision-theoretic approach to multi-source fuzzy information systems[J]. Knowledge-based systems, 2016, 91: 102-113.

[10]LIU Caihui, MIAO Duoqian, QIAN Jin. On multi-granulation covering rough sets[J]. International journal of approximate reasoning, 2014, 55(6): 1404-1418.

[11]别林斯里. 概率与测度[M]. 3版. 北京: 世界图书出版公司, 2007.

[12]ZHU W, WANG Feiyue. Reduction and axiomization of covering generalized rough sets[J]. Information sciences, 2003, 152: 217-230.

[13]YAO Yiyu. Three-way decisions with probabilistic rough sets[J]. Information sciences, 2010, 180(3): 341-353.

刘财辉，男，1979年生，副教授，主要研究方向为粗糙集、粒计算、机器学习、数据挖掘。发表学术论文20余篇，其中被SCI检索4篇，EI检索12篇。

蔡克参，女，1992年生，硕士研究生，主要研究方向为粒计算方法在农业信息化中的应用。

Multigranulation covering rough sets based on the union of minimal descriptions of elements

LIU Caihui， CAI Kecan

(Department of Mathematics & Computer Science, Gannan Normal University, Ganzhou 341000, China)

To generalize multigranulation rough sets to a covering-based approximation space, this paper proposes three kinds of covering-based multigranulation rough sets by employing the conditional probability between the target concept and the union of the minimal descriptions of elements. Based on new definitions, some basic properties of these models were investigated and their relationships with some existing covering-based multigranulation rough sets are revealed. The inter-relationship among the three new models is also explored. The discussions show that the proposed models are a special form of text model, as well as extensions of some existing covering-based multigranulation rough sets.

rough sets; multigranulation; conditional probability; covering; minimal description

10.11992/tis.201605034

网络出版地址：http://www.cnki.net/kcms/detail/23.1538.TP.20160808.0830.018.html

2016-05-31. 网络出版日期：2016-08-08.

国家自然科学基金项目(61305052，61403329，61663002).

刘财辉.E-mail：liu_caihui@163.com.

TP18

A

1673-4785(2016)04-0534-05