杂交型马鞍网壳结构参数化设计及形状优化

苏亚，鹿少博，鹿晓阳*，洪宁，陈亚若，李涛

(1.山东建筑大学 工程力学研究所,山东 济南 250101； 2．坦佩雷理工大学 建筑学院,芬兰 坦佩雷 FI-337203；3.济南锅炉集团 设计一处,山东 济南 250022)



杂交型马鞍网壳结构参数化设计及形状优化

苏亚1，鹿少博2，鹿晓阳1*，洪宁3，陈亚若3，李涛1

(1.山东建筑大学 工程力学研究所,山东 济南 250101； 2．坦佩雷理工大学 建筑学院,芬兰 坦佩雷FI-337203；3.济南锅炉集团 设计一处,山东 济南 250022)

杂交型网壳可以发挥各单一传统网壳的优点，在增大跨度的同时又可获得较高的经济效益。文章根据杂交型马鞍型网壳结构特点，采用APDL参数化设计语言研制了两类六种不同杂交型马鞍网壳参数化设计宏程序，运用ANSYS软件对其进行受力性能分析，并对受力性能最好的凯威特—联方(Kie-Lam)网壳进行了108种工况形状优化设计。结果表明：在同等工况下六种杂交型马鞍网壳中Kie-Lam最大位移为6.9mm和最不应力为25.1MPa均最小，受力最为合理；矢高f与网壳最不利应力成反比，f每增加1m最不利应力平均下降幅度最大为0.51MPa，随Ns变化没有统一规律；在S=60m、f=30m不变的情况下，存在一种工况Kn=8、Nx=12和Ns=8满足结构强度、刚度和稳定性前提下，使网壳结构总耗钢量最轻。

杂交型马鞍网壳；参数化设计；受力性能分析；形状优化设计

0　引言

随着大跨度、大空间建筑的日益普及，人们已不满足传统、单一网壳形式的直接运用，倾向于不同结构形式的组合、发挥各自的特点，形成满足建筑美学及合理、经济的新型结构形式[1]，杂交型网壳应运而生(如图1所示)。新型杂交空间结构因几何构造简单、力流传递清楚、室内建筑效果美观而受到工程设计人员的青睐[2]，杂交型球面、柱面网壳及马鞍型网壳已广泛应用于展览馆，影剧场，体育馆和音乐厅等场所[3-5]。

图1　杂交型网壳建筑结构实例图(a) 北京奥运会羽毛球馆；(b) 南京科学水利研究院河湖治理研究基地；(c) 中国石油大学青岛校区体育馆

杂交型马鞍网壳给人们带来舒适感且能增大结构跨度，改善肋环、施威德勒、联方单一网壳类型顶点应力集中及按凯威特、三向格子型网壳规律连接杆件较多的弊端，使网格单元分布均匀，获得较高的经济效益。文章应用APDL参数化设计语言，研制了两类六种杂交型马鞍网壳的参数化设计宏程序，并对它们进行了受力性能分析和基于离散变量两级形状优化设计[1]，其研究结论为杂交型马鞍网壳选型优化设计和推广应用提供依据。

1　杂交型马鞍网壳组合条件及几何描述

马鞍型网壳有五种基本网格形式：肋环型(Ribbedtype)、施威德勒型(Schwedlertype)、三向格子型(three-waygrid)、凯威特型(Kiewitttype)和联方型(Lamellatype)，不包括短程线(Geodesictype)型(基于球面正二十面体分割的思想)，实现杂交得满足两个条件：(1) 在过渡圈上两种结构形式的节点数必须相同;(2) 杂交是为了实现优化结构形式的目的，即改善结构的受力也可能改变结构重量的杂交形式。凯威特每圈的节点数都是环向区域份数的整数倍和三向格子在过渡区不满足节点数相同，肋环、施威德勒和联方之间不满足条件(2)，考虑到条件(2)，肋环、施威德勒、联方只能为下层分别和凯威特、三向格子杂交。因此两类六种杂交型马鞍网壳模式出现。第一类为凯威特—肋环杂交型(简记为Kie-Rib)，凯威特—施威德勒杂交型(Kie-Sch)，凯威特—联方杂交型(Kie-Lam)；第二类为三向格子—肋环杂交型(thr-Rib)，三向格子—施威德勒杂交型(thr-Sch)，三向格子—联方杂交型(thr-Lam)。杂交型马鞍网壳主要几何参数有：跨度S、矢高f、环向区域份数Kn(对应棱角数)、上部结构径向圈数Ns和径向节点圈数Nx(对应网格密度)。图2以凯威特—肋环杂交型马鞍网壳为例描述了其主要几何参数。

2　两类六种杂交型马鞍网壳的参数化设计

借鉴拓展型型球面网壳、椭圆水平投影双曲抛物面网壳和折板网壳结构参数化设计的建模思想[6-8]，研制了两类六种杂交型马鞍网壳的参数化设计宏程序，限于篇幅，仅以凯威特—肋环杂交型马鞍网壳(Kie-Rib)参数化设计为例进行说明。

2.1凯威特—肋环杂交型马鞍网壳参数化设计

在笛卡尔坐标系下给定S、f、Kn、Nx、Ns，圆形水平投影马鞍型曲面方程由式(1)表示为

(1)

式中:S为跨度，m;f为矢高，m;x、y、z为节点坐标。

① 计算节点坐标、并定义节点编号：首先建立凯威特型节点，令顶点为1号节点，用APDL中循环语句[9]，由顶点向外依次进行节点编号，在平面上利用等分圆心角法计算出网壳第i圈节点数Kn×i，第i (1≤i≤Ns)圈第j (1≤j≤Kn×i)份上的节点编号为j+i×Kn×(i-1)/2+1，节点坐标为： x=i×(S/(2Nx))×cos(360×(j-1)/(i×Kn))，y=i×(S/(2Nx))×sin(360×(j-1)/(i×Kn))，z=2f×(x2-y2)/S2。然后建立下部结构肋环型节点，从第Ns+1圈开始建立节点，由内向外依次进行，第j+Kn×(Ns×Ns+Ns)/2+1+Ko×(i-Ns-1) (式中Ko=Ns×Kn下同，且Ns+ 1≤i≤Nx， 1≤j≤Ko)号节点坐标为：x= i×(S/(2Nx))×cos(360/Ko×(j-1))，y=i×(S/(2Nx))×sin(360/ Ko×(j-1))，z=2f×(x2-y2)/S2。

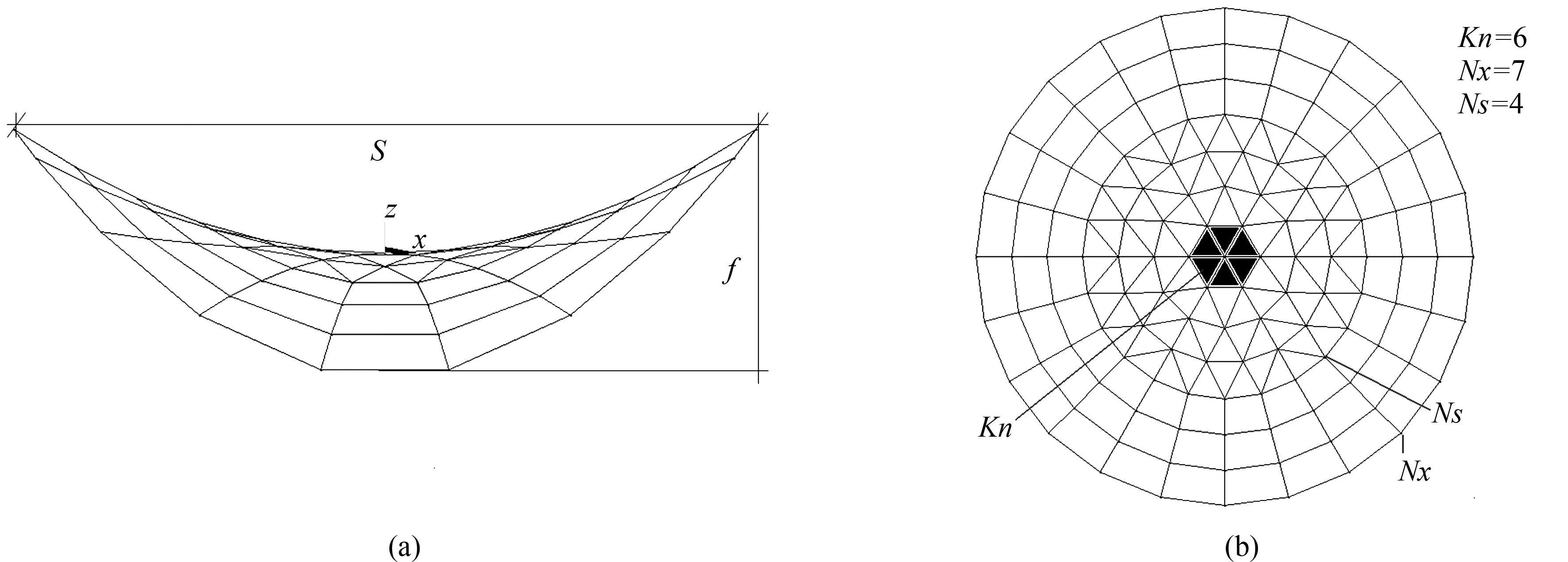
图2　凯威特-肋环杂交型马鞍网壳宏观几何参数图(a) Kie-Rib正视图；(b) Kie-Rib俯视图

② 杆件连接：首先进行凯威特型杆件连接，据节点编号利用APDL循环语句按节点分布规律进行环向和径向杆件连接。第i (1≤i≤Ns)圈第j (1≤j≤Kn×i-1)对称区域环向杆件是连接节点j+i×Kn×(i-1)/2+1和j+i×Kn×(i-1)/2+2， 第i圈最后一对称区域的环向杆件是由圈末节点j+i×Kn×(i-1)/2+1和首节点i×Kn×(i-1)/2+1+Kn×i连接而成。径向杆件利用三重循环命令、按节点分布规律进行杆件连接。其次从第Ns+1圈杆件的连接方式变为肋环型，即第i(Ns+1≤i≤Nx)圈第j(1≤j≤Ko-1)对称区域环向杆件是连接节点j+Kn×(Ns×Ns+Ns)/2+1+Ko×(i-Ns-1)和j+Kn×(Ns×Ns+Ns)/2+Ko×(i-Ns-1)+2， 第i圈最后一对称区域的环向杆件是由节点Kn×(Ns×Ns+Ns)/2+2+Ko×(i-Ns-1)和节点Kn×(Ns×Ns+Ns)/2+1+Ko×(i-Ns-1)+Ko连接而成。径向杆件的连接是第Ns+1圈和第Nx圈之间的径向的节点相连，由内向外循环，第i圈第j对称区域节点j+Kn×(Ns×Ns+Ns)/2+1+Ko×(i-Ns-1)和节点j+Kn×(Ns×Ns+Ns)/2+1+Ko×(i-Ns)相连而成。最后过渡区(即第Ns圈和第Ns+1圈之间)的杆件连接，因节点数相同，上下两环节点相连即可。

(3) 施加约束和荷载：杂交型马鞍网壳最外一圈节点施加固定铰约束(限制x、y、z三个方向的线位移)，等效荷载施加在网壳所有节点上。

2.2两类六种杂交型马鞍网壳参数化设计实例

图3为第一类和第二类杂交型马鞍网壳在跨度S=60m、f=30m、Kn=6、Nx=8和Ns=5时参数化设计实例图。

3　两类六种杂交型马鞍网壳受力性能分析

3.1施加约束和载荷

选取S=60m、f=30m、f/S=1/2、Kn=6、Nx=12、Ns=9两类六种杂交型马鞍网壳进行受力分析。杆件采用Q235钢管，钢材密度为7850kg/m3，弹性模量2.06×1011N/m2，泊松比0.3；杆件单元选ANSYS中BEAM4梁单元，杆件截面为Φ219×16；采用理想弹塑性材料模型，不考虑材料的强化，屈服前钢材为线弹性，网壳最外一圈节点采用固定铰支座(只限制x、y、z三个方向线位移，不限制转动)，考虑结构自重，屋面施加2.35kN/m2均布荷载[10]。

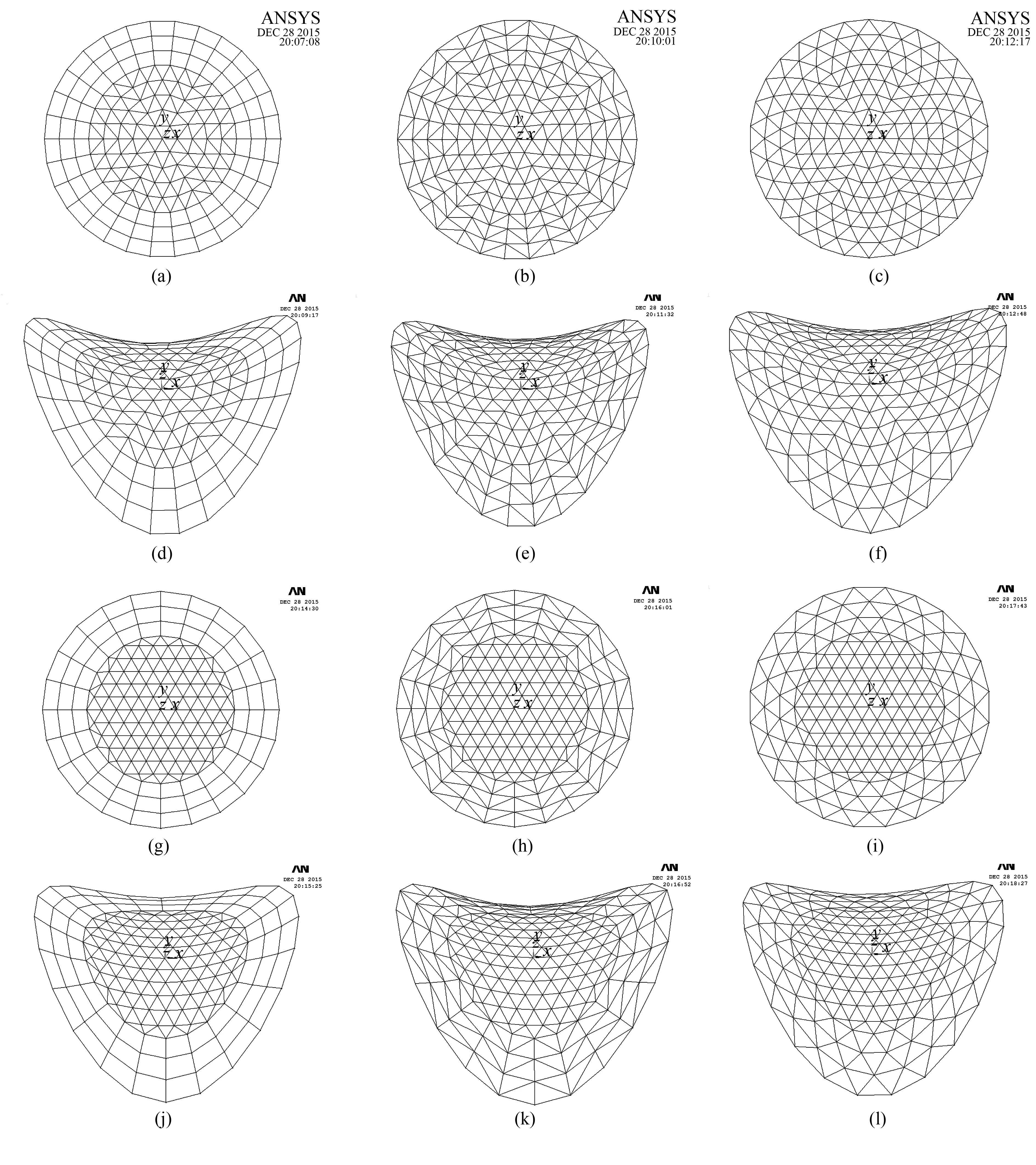
图3　六种杂交型马鞍网壳参数化设计图(a) Kie-Rib俯视图；(b) Kie-Sch俯视图；(c) Kie-Lam俯视图；(d) Kie-Rib轴测图；(e) Kie-Sch轴测图；(f) Kie-Lam轴测图；(g) thr-Rib俯视图；(h) thr-Sch俯视图；(i) thr-Lam俯视图；(j) thr-Rib轴测图；(k) thr-Sch轴测图；(l) thr-Lam轴测图

3.2两类六种杂交型马鞍网壳受力性能分析

空间网格结构技术规程[11]中3.5.1规定，单层网壳节点最大挠度值不宜超过最短跨度的1/400，许用应力为钢材的强度设计值215MPa。其中,S=60m，结构允许最大位移为S/400=0.15m；图4～7分别为第一类和第二类杂交型马鞍网壳在S=60m、f=30m、f/S=1/2、Kn=6、Nx=12和Ns=9下的位移云图和最不利应力云图。

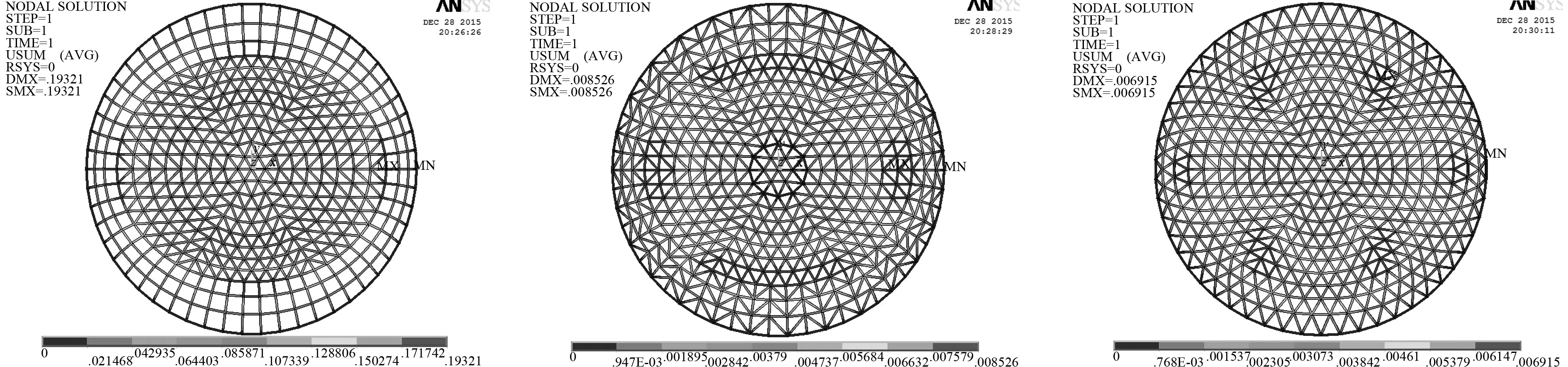
图4　第一类杂交型马鞍网壳位移云图(a) Kie-Rib马鞍网壳位移云图；(b) Kie-Sch马鞍网壳位移云图；(c) Kie-Lam马鞍网壳位移云图

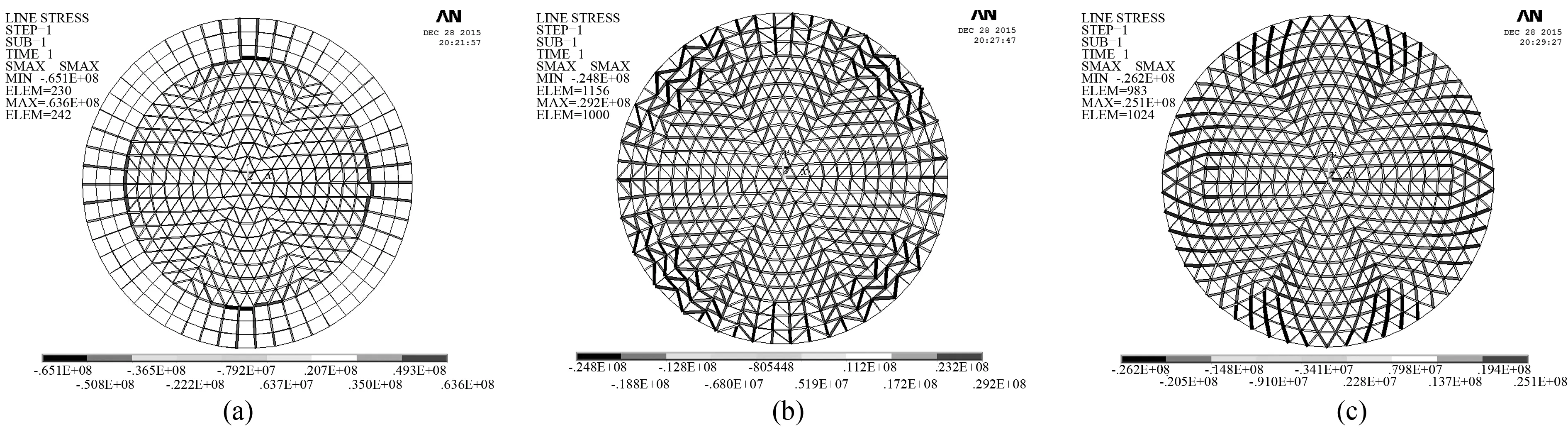
图5　第一类杂交型马鞍网壳最不利应力云图(a) Kie-Rib马鞍网壳应力云图；(b) Kie-Sch马鞍网壳应力云图；(c) Kie-Lam马鞍网壳应力云图

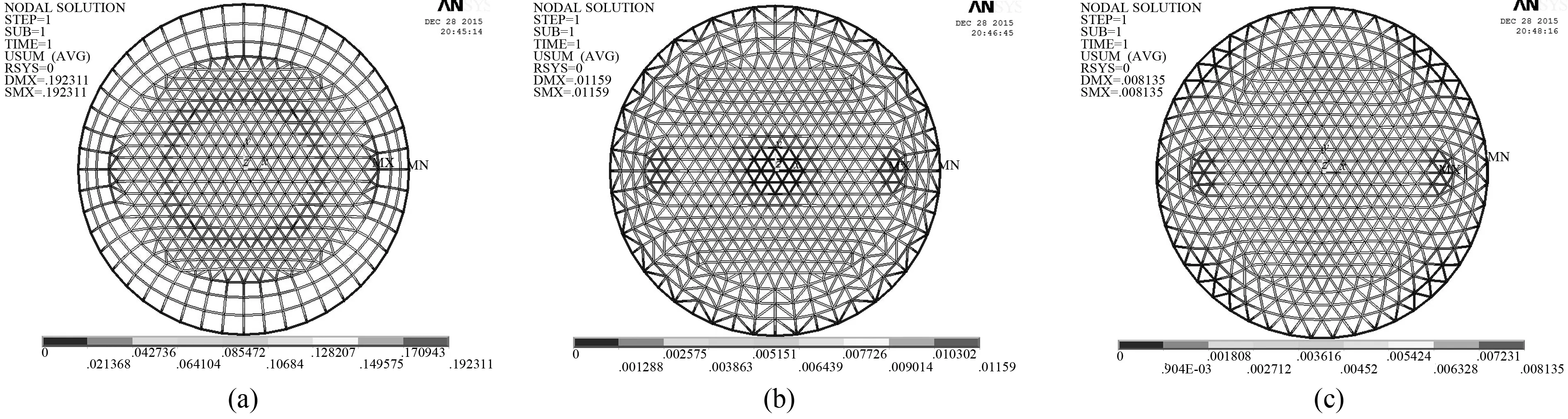
图6　第二类杂交型马鞍网壳位移云图(a) thr-Rib马鞍网壳位移云图；(b) thr-Sch马鞍网壳位移云图；(c) thr-Lam马鞍网壳位移云图

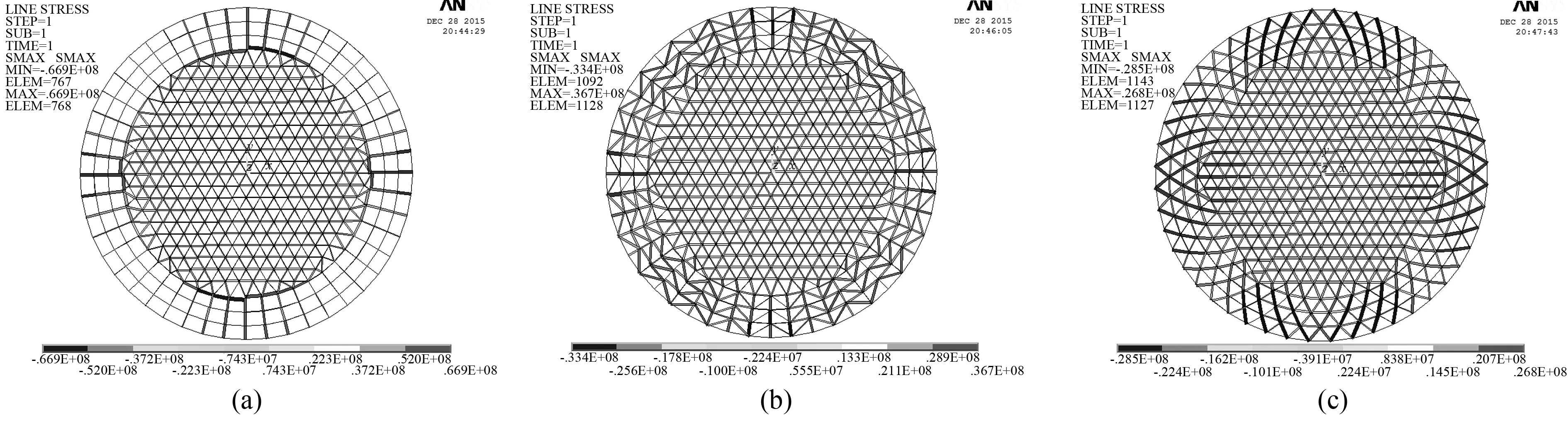
图7　第二类杂交型马鞍网壳最不利应力云图(a) thr-Rib马鞍网壳应力云图；(b) thr-Sch马鞍网壳应力云图；(c) thr-Lam马鞍网壳应力云图

由图4～7可知，六种杂交型网壳在竖向荷载作用下，主要由索向受拉杆件和拱向受压杆件来承担，中心顶点处的应力和位移均很小，成功避免了单一网壳类型顶点应力集中现象；其中，Kie-Rib和thr-Rib网壳位移和最不利应力较大区域发生在拱向和索向过渡区附近；Kie-Sch和Kie-Lam网壳位移较大的区域发生在六条主肋过渡区偏上一到两圈，分布的区域较均匀；thr-Sch和thr-Lam网壳位移较大的区域发生在索向过渡区附近，这四种网壳最不利应力较大的区域普遍出现在拱向和索向边缘附近，说明此处杆件强度相对较弱，设计施工时可有针对性的加强。但是，Kie-Rib和thr-Rib网壳在文中工况下最大位移分别为0.192942 和0.192001m均大于结构允许挠度0.15m，整体刚度较弱，不适合中大跨度结构，结构必须具有一定的刚度来抵抗结构的变形[12]。thr-Lam、Kie-Sch、thr-Sch的最大位移和最不利应力分别为0.008132、0.008526和0.011586m和26.5MPa、29.2MPa、36.7MPa。而Kie-Lam的最大位移0.006912m和最不利应力25.1MPa在同工况下均最小，远小于结构允许挠度0.15m和许用应力215MPa，受力合理，可优先选用。

表1、2 给出了两类杂交型马鞍网壳在S=60m、f=30m、Kn=6、Nx=12和Ns=4～11时的最大位移和最不利应力值；表3、4给出了两类杂交型马鞍网壳在S=60m、Kn=6、Nx=12、Ns=9和f=15m～50m时的最大位移和最不利应力值。其中，最不利应力是负值，代表压应力；正值，代表接应力。

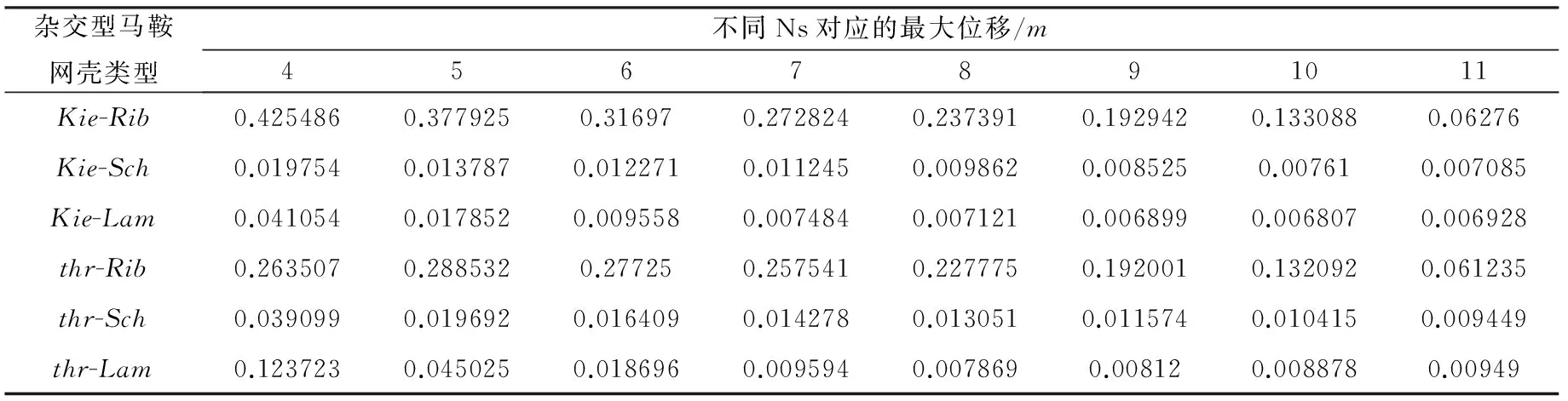
表1　六种网壳不同的Ns对应的最大位移

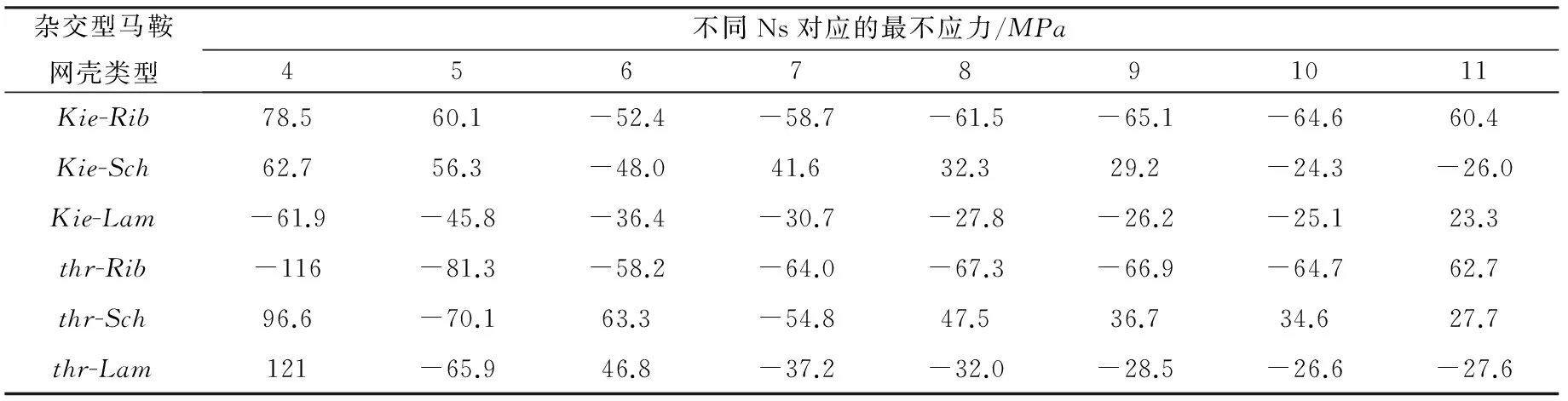
表2　六种网壳不同的Ns对应的最不利应力

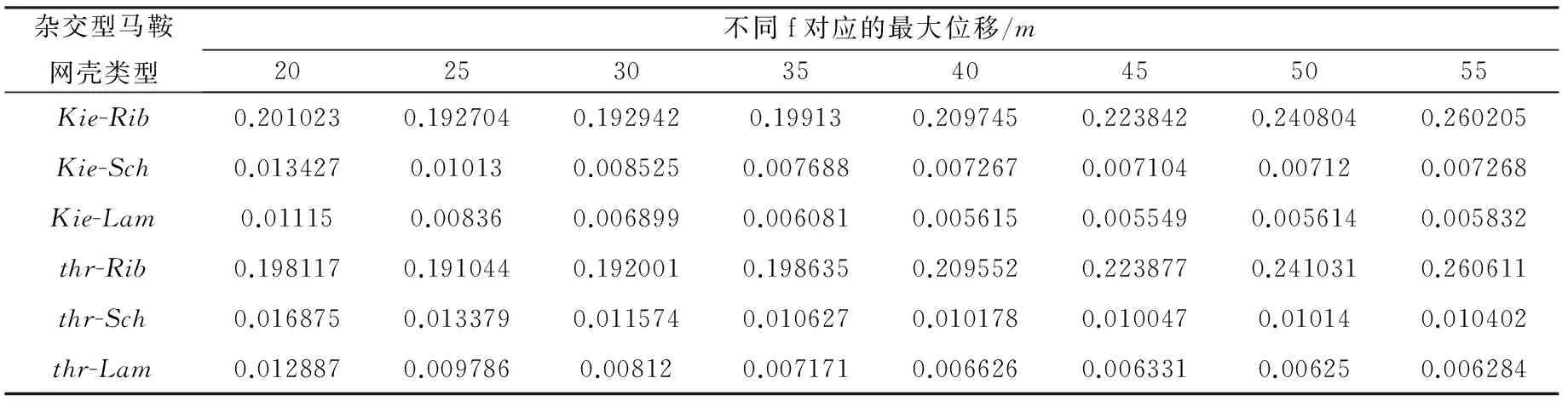
表3　六种网壳不同的f 对应的最大位移

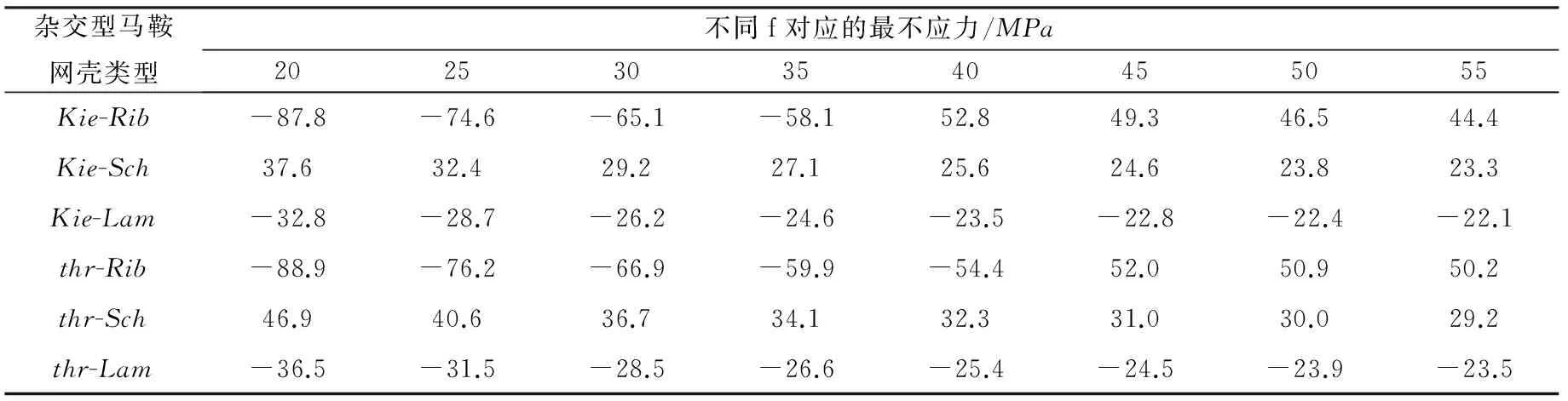
表4　六种网壳不同的 f 对应的最不利应力

通过上述表格可知：

(1) 由表1、2知，随着Ns的增多：Kie-Lam和thr-Lam网壳的最大位移呈现先减小后增大的趋势，其它四种杂交型马鞍网壳的最大位移均呈现递减的规律性变化，但变化幅度不是很大(最大幅度不超过毫米级)，但是Kie-Rib和thr-Rib网壳在Ns=4～9时最大位移均大于结构的允许位移0.15m，结构刚度已难以满足实用要求；Kie-Rib、thr-Rib的最不利应力变化先减小后增大又变小波动性的变化，Kie-Sch、thr-Lam呈现先减小后增大的变化规律，而Kie-Lam、thr-Sch最不利应力则呈现递减的变化规律。

(2) 由表3、4知，随着f的增大，六种杂交型马鞍网壳的最大位移均呈现先减小后增大的规律性变化，各自都存在结构合适矢高f使其整体位移最小；而最不利应力却呈现递减的规律性变化，Kie-Sch、thr-Sch以索向杆件受拉为主，Kie-Lam、thr-Lam以拱向杆件受压为主，而Kie-Rib、thr-Rib矢高f较小时以拱向杆件受压为主，f较大时以索向杆件受拉为主。f 每增加1m，最不利应力下降幅度最大的thr-Sch平均仅减少0.51MPa，相对下降1.08%，最不利应力下降幅度最小的Kie-Lam平均减少0.31MPa，相对下降0.93%(除Kie-Rib，thr-Rib外)，f增大对受力性能效果的改善并不显著。

4　凯威特—联方杂交型马鞍网壳形状优化分析

以网壳结构的Kn、Nx、Ns为设计变量，采用离散变量两级形状优化方法对其进行形状优化，分析网格(Kn、Nx、Ns)变化对网壳结构耗钢量的影响。

4.1基于离散变量两级优化方法

第1级优化赋予初始杆件型钢离散集中最小的截面尺寸和空心焊接球节点许用离散集最小型号，对其静力分析，得到每组杆件的最不利应力，最大长细比等中间变量，增大杆件截面使其满足应力、长细比，杆件局部稳定性和节点约束；第2级优化是以1级优化的解作为初始解，满足结构整体位移和整体稳定性约束，满足约束条件优化结束，否则，采用“相对差商法[13]”，增大“相对差商”最小的那组杆件截面和节点型号，让全局约束条件得到满足，又使整体结构耗钢量增加最少，反复迭代直到全局约束全部满足[14-16]。

4.2网壳形状优化数学模型

设计变量：杆件截面积Ai(i=1，2，m1)，节点体积Vj(j=1，2，n)；目标函数网壳结构的最轻总重量由式(2)表示为

(2)

式中：m1为杆件组数；n为节点总数；Ai为第i 根杆件的面积，m2；Vj为第j个球节点的体积，m3；ρi、ρj分别为杆件和球节点钢材的密度，kg/m3；li为第i根杆件的几何长度，m；Vj=πD2t；D为球节点直径，m；t为焊接空心球节点的壁厚，m。

应力约束：

(3)

式中：N为杆件轴力，N；A为杆件截面积，m2；My和Mz分别为绕局部二轴和局部三轴的弯矩，N·m；Wy和Wz分别为两主轴的截面抗弯模量，m3；γy和γz为与截面模量相应的塑性发展系数，均取1.15，σ=215MPa为杆件的屈服应力。

弯矩作用平面内稳定性约束由式(4)表示为

(4)

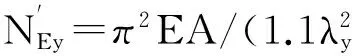
弯矩作用平面外稳定性约束由式(5)表示为

(5)

式中：φb为均匀弯曲的受弯构件整体稳定系数，取1.0；My为所计算构件段范围内的最大弯矩，N·m；η为截面影响系数，闭口截面η=0.7,β1y为等效弯矩系数，取1.0。

长细比约束由式(6)表示为λ≤[λ]

(6)

式中:[λ]为杆件的长细比，压杆取150，拉杆取250。

节点约束，空心球的最小直径由式(7)表示为

(7)

式中：d1为两相邻钢管中较大外径，mm；ds为两相邻钢管中较小外径，mm；θ为两相邻杆件轴线间的夹角，rad；αn为两相邻钢管间的净距，一般取αn=10mm。

4.3数值算例

以受力性能较好的凯威特—联方杂交型(Kie-Lam)马鞍网壳为例进行形状优化设计，给定S=60m、f=30m、Kn=6～16步长为2、Nx=10～12步长为1和Ns=4～9步长为1，共108个工况下，在结构满足强度、刚度、局部稳定性和整体稳定性约束条件下，以网壳结构总耗钢量最小为目标函数，寻求Kn、Nx和Ns最优组合，形状优化得到的最优组合为Kn=8、Nx=12和Ns=8，总耗钢量最小为27220.39kg。文中仅列出Kn分别为6、8、10和Nx为10～12、Ns为4～9时所对应的耗钢量图。

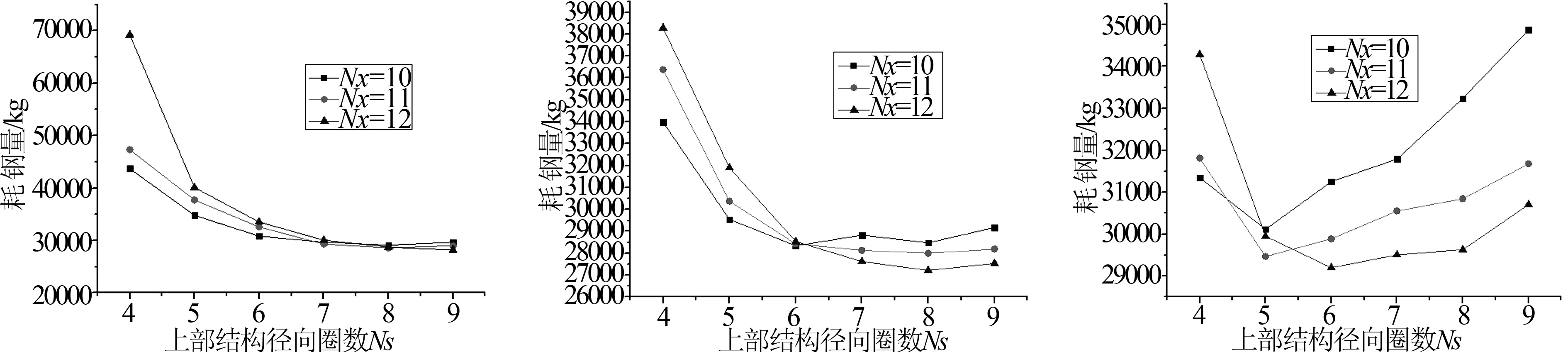
图8　形状优化对应的耗钢量图(a) Kn=6对应的耗钢量；(b) Kn=8对应的耗钢量；(c) Kn=10对应的耗钢量

由图8可知，当S =60m、f =30m时，Kie-Lam杂交型马鞍网壳在满足强度、刚度、稳定性前提下，Kn、Nx和Ns的匹配与网壳耗钢量呈现较为复杂的非线性关系，网格数的变化对用钢量比较敏感，特别当Ns=4变到Ns=5时，网壳耗钢量下降均较大，最大下降量当属Kn=6、Nx=12时达到50%左右。当Kn=6时，耗钢量是随着Ns的增加逐渐减小的，说明网壳杆件和节点增多的用钢量相对于杆件截面变小的用钢量的幅值偏小；当Kn>6 时，耗钢量均随着Ns的增加呈现先减小后增大的变化，受力合理的网格数一旦确定，则网格密度的增加是必会引起用钢量的增加，但对网壳结构的受力性能改善并不大，一味的增大网格密度只会增加结构成本。网壳结构在形状优化得到的最优网格数下既能保证结构安全性，又可获得较高经济效益，为降低实际工程造价提供了一条可靠途径。

5　结论

文章对两类六种杂交型马鞍网壳进行了参数化设计，分析了S=60m时网壳静力性能以及108种工况下Kie-Lam形状优化，结果表明：

(1) 在f/s=1/2、Kn=6、Nx=12和Ns=9时，两类网壳顶点处应力和位移均很小，避免了单一网壳顶点附近应力集中现象，Kie-Lam最大位移6.9mm和最不利应力25.1MPa均最小，受力合理，可优先选用，其次thr-Lam，Kie-Sch，thr-Sch。但是Kie-Rib和thr-Rib最大位移分别为192.9mm和192mm均大于结构允许挠度150mm，整体刚度较弱，不适合中大跨度结构。

(2) 最不利应力随Ns变化没有统一规律，却与f成反比，f每增加1m最不利应力平均下降幅度最大为0.51MPa，相对降低1.08%(thr-Sch)对改善受力性能并不显著；但存在合适f使其整体挠度各自最小，唯一Ns使Kie-Lam和thr-Lam整体挠度最小。

(3) 网格数对网壳耗钢量影响较敏感，甚者可使其降低50%，当Kn=8、Nx=12和Ns=8时可保证Kie-Lam既安全同时总耗钢量最轻，这为实际工程设计提供了有意的参考。

[1]鹿晓阳,赵晓伟,陈世英．离散变量网壳结构优化设计[M]. 北京：中国建筑工业出版社,2013.

[2]张志宏,李志强,董石麟．杂交空间结构形状确定问题的探讨[J]．工程力学,2010,27(11):56-62.

[3]张爱林,葛家琪,刘学春．2008奥运会羽毛球馆大跨度新型弦支穹顶结构体系的优化设计选定[J]．建筑结构学报,2007, 28(6):1-4.

[4]王澈泉,申波,马克俭,等．正三角形立体管桁架与单层柱面网壳杂交结构的设计与分析[J]．工业建筑,2014, 44(6):130-134.

[5]王毅,王雪生,朱忠义,等．中国石油大学(青岛校区)体育馆主馆屋盖结构选型与研究[J]．建筑结构,2009, 39(12):71-73．

[6]洪宁．拓展型球面网壳参数化建模与形状优化设计[D]．济南：山东建筑大学,2013.

[7]安然．椭圆水平投影双曲抛物面网壳参数化设计及抗震性能分析[D]．济南：山东建筑大学,2015.

[8]鹿晓阳,张萍,陈世英,等. 折板网壳结构参数化设计及受力特点分析[J]．山东建筑大学学报,2013,28(1):1-6．

[9]龚曙光,谢桂兰．ANSYS参数化编程与命令手册[M]．北京：机械工业出版社,2010.

[10]GB50009—2012，建筑结构荷载规范[S]．北京：中国建筑工业出版社,2012.

[11]JGJ7—2010，空间网格结构技术规程[S]．北京：中国建筑工业出版社,2010.

[12]张毅刚,薛素铎,杨庆山，等．大跨空间结构[M]. 北京：机械工业出版社,2014.

[13]孙焕纯,柴山,王跃方,等．离散变量结构优化设计[M]．大连：大连理工大学出版社,2002.

[14]陈世英,郭玉霞,鹿晓阳．单层球面网壳结构选型优化设计[J]．建筑钢结构进展,2010,12(8):46-50．

[15]陈世英,鹿晓阳,綦文,等．凯威特网壳最优网格研究[J]．建筑钢结构进展,2013,15(2):21-25．

[16]陈世英,鹿晓阳,王洪利,等．截面优化对网壳结构应力、位移和整体稳定性影响分析[J]．空间结构,2014, 20(1):45-52．

(学科责编：李雪蕾)

Parametric modeling and shape optimization ofhybridsaddlereticulatedshell

Su Ya1，Lu Shaobo2，Lu Xiaoyang1*,et al.

(1. Research Institute of Engineering Mechanics, Shandong Jianzhu University, Jinan250101, China；2．School of Architecture, Tampere University of Technology, FI-33720, Finland； 3. The First Design Department, Jinan Boiler Group Company?Limited, Jinan250022, China)

Hybridshellcantaketheadvantagesofeachsingletraditionalshell,whichcannotonlyincreasethespanbutalsoobtainhighereconomicbenefitsatthesametime.MacroprogramofsixkindshybridsaddlereticulatedshellparametricdesignweredevelopedbyANSYSparameterofdesignlanguageaccordingtosaddlereticulatedshellfeatures.Themechanicalperformanceswereanalyzedandtheshapeoptimizationunder108kindsofworkingconditionforKiewitt-LamellaSaddleReticulatedShellwasstudiedwithobjectivefunctionofminimumsteelconsumptionandshapeoptimizationdesignvariablesKn(ringtosymmetricregionalcopiesnumber), Nx(radialnoderingnumber), Ns(theupperstructureofradialring).Theresultsshowed:ThemaximaldisplacementandthemostunfavorablestressofKiewitt-Lamellawere6.9mmand25.1Mpa,whichweretheleastofsixkindshybridsaddlereticulatedshellthatitsmechanicalperformancewasthemostreasonableunderthesamecondition.Thevectorheightfwasinverselyproportionaltothemostunfavorablestress,existingsuitablefmadetheirrespectiveoveralldeflectionminimum,andNschangedthelawoftheunityonboth;WhenspanS=60mandthef=30mwerecertain,existingonekindofworkingconditionofKn=8, Nx=12andNs=8underthepreconditionsatisfiedthestrength,stiffnessandstability,makingthetotalsteelconsumptionofreticulatedshelllightest.

hybridsaddlereticulatedshell;parametricdesign;mechanicalperformancesanalysis;shapeoptimizationdesign

2015-12-06

山东省研究生创新计划项目(SDYY08038);山东省自然科学基金项目(ZR2010AM016)

苏亚(1987-)，男，在读硕士，主要从事结构优化设计等方面的研究.E-mail：suya0310@163.com

*:鹿晓阳(1955-)，男，教授，博士，主要从事结构受力分析与优化设计、材料加工工艺等方面的研究.E-mail:lxy5504@yahoo.com.cn

1673-7644(2016)01-0038-09

TU393.3，TU311.41

A