火灾中带裂缝钢筋混凝土梁承载力算法研究
王玉镯,王灿灿,傅传国
(山东建筑大学 土木工程学院,山东 济南 250101)
火灾中带裂缝钢筋混凝土梁承载力算法研究
王玉镯,王灿灿,傅传国
(山东建筑大学 土木工程学院,山东 济南 250101)
火灾中带裂缝钢筋混凝土梁的承载能力研究可为工程实际应用提供参考。文章利用有限元分析软件ABAQUS对火灾中带裂缝钢筋混凝土梁内部的温度场进行分析,阐明了火灾中带裂缝钢筋混凝土梁内部温度场的分布规律,根据其分布规律确定了在不同耐火时刻有裂缝钢筋混凝土梁300和800 ℃的等温线,结合已有的高温下钢筋混凝土梁承载力计算公式,提出了火灾中带裂缝钢筋混凝土梁承载力计算公式。结果表明:在同样的受火条件下有裂缝时钢筋混凝土梁中钢筋位置的温度比是无裂缝时钢筋混凝土梁中钢筋位置的温度高55%~144%;有五条裂缝的钢筋混凝土梁中钢筋位置的温度比有一条裂缝的钢筋混凝土梁中钢筋位置的温度高2.7%~11.5%;带裂缝钢筋混凝土梁的承载力比无裂缝钢筋混凝土的承载力低47%~82%。
钢筋混凝土梁;火灾中;裂缝;温度场;极限承载力
0 引言
混凝土的抗压强度很高但抗拉强度却很低,所以混凝土构件在拉应力很小时也会出现裂缝,而混凝土构件由于受力特点不可避免的会有拉应力的存在,因此钢筋混凝土梁出现裂缝是一种普遍现象。在实际工程中可能由于材料的热胀冷缩和混凝土内外温差等原因使钢筋混凝土梁表面产生微小的裂缝。虽然微小的裂缝在常温下不影响钢筋混凝土梁的承载能力,但在火灾中,这些裂缝就可能会对结构的承载能力造成影响。因此,有必要对火灾中带裂缝钢筋混凝土梁的承载力性能进行研究。
国内外学者对高温下钢筋混凝土梁开展了很多的试验研究和理论分析,得出了高温下钢筋混凝土梁极限承载力的计算公式[1-12]。杨建平等在合理假定的基础上提出一种计算钢筋混凝土受弯构件高温承载力的实用简化计算方法[4]。Wang等根据材料在高温下的力学简化模型得到的型钢混凝土梁等效截面计算公式,建立了火灾下型钢混凝土梁承载能力极限状态的计算公式[6]。方猛提出了高温下混凝土强度三台阶模型的计算方法[7]。刘殿魁等介绍了三面受火钢筋混凝土简支梁等效火灾荷载的计算公式,得到等效火灾荷载和耐火极限[8]。综上所述,以上研究均为高温下无裂缝钢筋混凝土梁的极限承载力性能的研究。目前,还没有查到关于火灾中带裂缝钢筋混凝土梁的极限承载力研究。在受弯作用下,由于混凝土梁内钢筋锈蚀后体积的膨胀造成了混凝土保护层胀裂损伤,在梁的下翼缘的位置会出现沿钢筋方向的裂缝。文章选取使用时间较长、含水率较低、龄期较长的混凝土梁构件,并且在梁的下翼缘的位置出现沿钢筋方向的裂缝,这样的破坏属于耐久性破坏。文章以这种典型的裂缝为代表,采用有限元分析软件ABAQUS对这种带裂缝钢筋混凝土梁截面的温度场进行数值模拟得到其温度场的变化规律,参考高温下无裂缝钢筋混凝土梁极限承载力的简化计算公式[6],利用高温下钢筋和混凝土的本构关系[4-6],推导了火灾中带裂缝钢筋混凝土梁承载能力的计算公式,为工程实际应用提供参考。
1 带裂缝钢筋混凝土梁温度场数值模拟
1.1模型选取
文章利用有限元软件ABAQUS[1,13-16]对钢筋混凝土梁的内部温度场进行数值模拟。考虑实际中梁受力状态,选取六个截面尺寸相同而裂缝状态不同的梁构件作为研究对象,选择高h、宽b的梁截面尺寸,梁截面裂缝状况分别为:无裂缝、有一个裂缝、有两个裂缝、有三个裂缝、有四个裂缝、有五个裂缝共六种状态。在梁的下翼缘且沿纵向受力钢筋方向出现裂缝,其截面深度为30 mm、宽度为0.3 mm,截面形状为矩形,梁截面如图1所示。
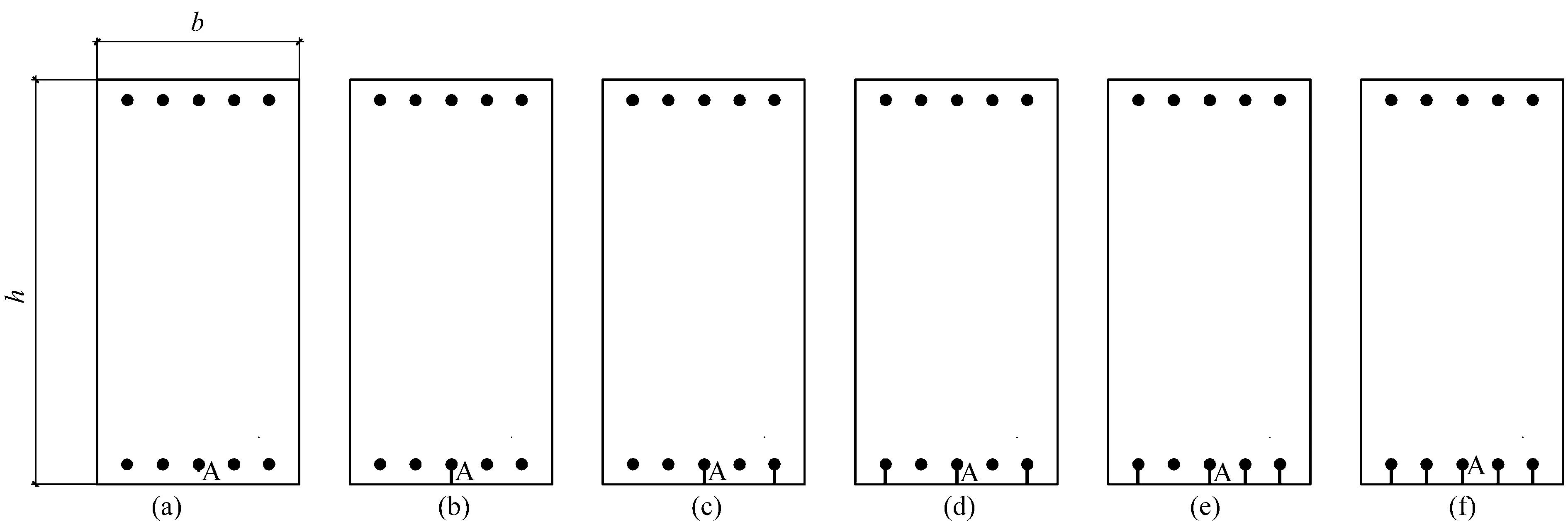
图1 梁不同裂缝的截面图(a) 无裂缝;(b)有一条裂缝(c)有两条裂缝;(d)有三条裂缝;(e)有四条裂缝;(f)有五条裂缝
1.2参数选取分析
升温曲线采用ISO—834标准升温曲线,所有构件均采用三面受火状态进行分析。受火面边界条件同时采用对流和辐射条件,受火面的对流换热系数 25 W/(m·℃),形状系数取值为1,综合辐射系数为0.5,非受火面也采取对流和辐射边界条件,非受火面的对流换热系数 9 W/(m·℃)。比热容为1000 J/(kg·K)[9]。
采用欧洲规范[9],导热系数λc由式(1)表示为
20 ℃≤T≤1200 ℃
(1)
式中:λc为温度为T时混凝土的热传导系数,W/(m·K);T为混凝土温度,℃。
1.3温度场分布状况分析
文章在进行温度场计算时并未考虑钢筋的传热作用。网格部分采用六面体单元,混凝土采用DC3D8单元进行传热分析。得到在同一个受火时间、裂缝条数不同时温度场的分布状况,如图2所示。
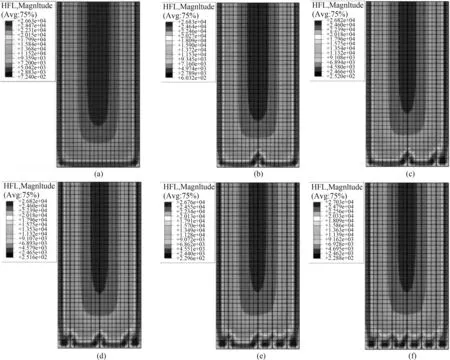
图2 钢筋混凝土梁截面温度云图(a)无裂缝;(b)有一条裂缝;(c)有两条裂缝;(d)有三条裂缝;(e)有四条裂缝;(f)有五条裂缝
为了分析裂缝对温度场的影响,选取受拉钢筋处的位置作为参考点(即图1中点A),得到点A在不同状态下最高温度变化曲线,如图3所示。参考点A处最高温度的汇总表见表1。从图3的曲线上可看出:火灾开始时,混凝土的温度上升速度较快,但随着时间变长,上升速度变缓。从由图3和表1中可看出:
(1) 在相同的受火时间下,无裂缝钢筋位置和有裂缝钢筋位置之间的温度相差很大。开始时,有无裂缝钢筋位置的温度都是20 ℃。在受火时间为30 min时,有裂缝比无裂缝钢筋位置的温度高288 ~350 ℃。受火时间为60 min时,有裂缝比无裂缝钢筋位置的温度高出331 ~380 ℃。受火时间为180 min时,有裂缝比无裂缝钢筋位置的温度高378 ~409 ℃。说明裂缝对该位置温度的影响很大,有裂缝比无裂缝钢筋位置的温度高55%~140%。
(2) 在相同的受火时间下,不同裂缝之间钢筋位置的温度相差不大。受火时间为30 min时,有五条裂缝比有一条裂缝钢筋位置的温度高64 ℃。受火时间为60 min时,有五条裂缝比有一条裂缝钢筋位置的温度高49 ℃。受火时间为180 min时,有五条裂缝比有一条裂缝钢筋位置的温度高31 ℃。说明当裂缝存在时,裂缝条数对该位置的温度影响不大,。
(3) 钢筋混凝土梁在同一状态下,随着受火时间的增加,钢筋位置的温度随之增大。受火时间从30 min变为240 min时,无裂缝钢筋位置的温度升高了389 ℃,有一条裂缝钢筋位置的温度升高了469 ℃,有五条裂缝钢筋位置的温度升高了433 ℃。说明随着受火时间的增大,有裂缝钢筋位置的温度与无裂缝钢筋位置的温度增加趋势是相同的。
⑷ 无裂缝钢筋混凝土梁在20 min左右的时候出现了一段水平段,即随着升温时间的增加温度保持100 ℃左右,并且水平段比较明显,这是因为无裂缝钢筋混凝土梁中含有水分。但选取的构件为含水率比较低的钢筋混凝土梁,所以与新浇筑的混凝土构件相比,水平段保持的时间较短。对于有裂缝的构件,水平段相对不明显。这说明当裂缝存在时,含水率对有裂缝钢筋位置的温度和无裂缝钢筋位置的温度的影响不太一样。这是因为由于裂缝的存在,水分蒸发过快。
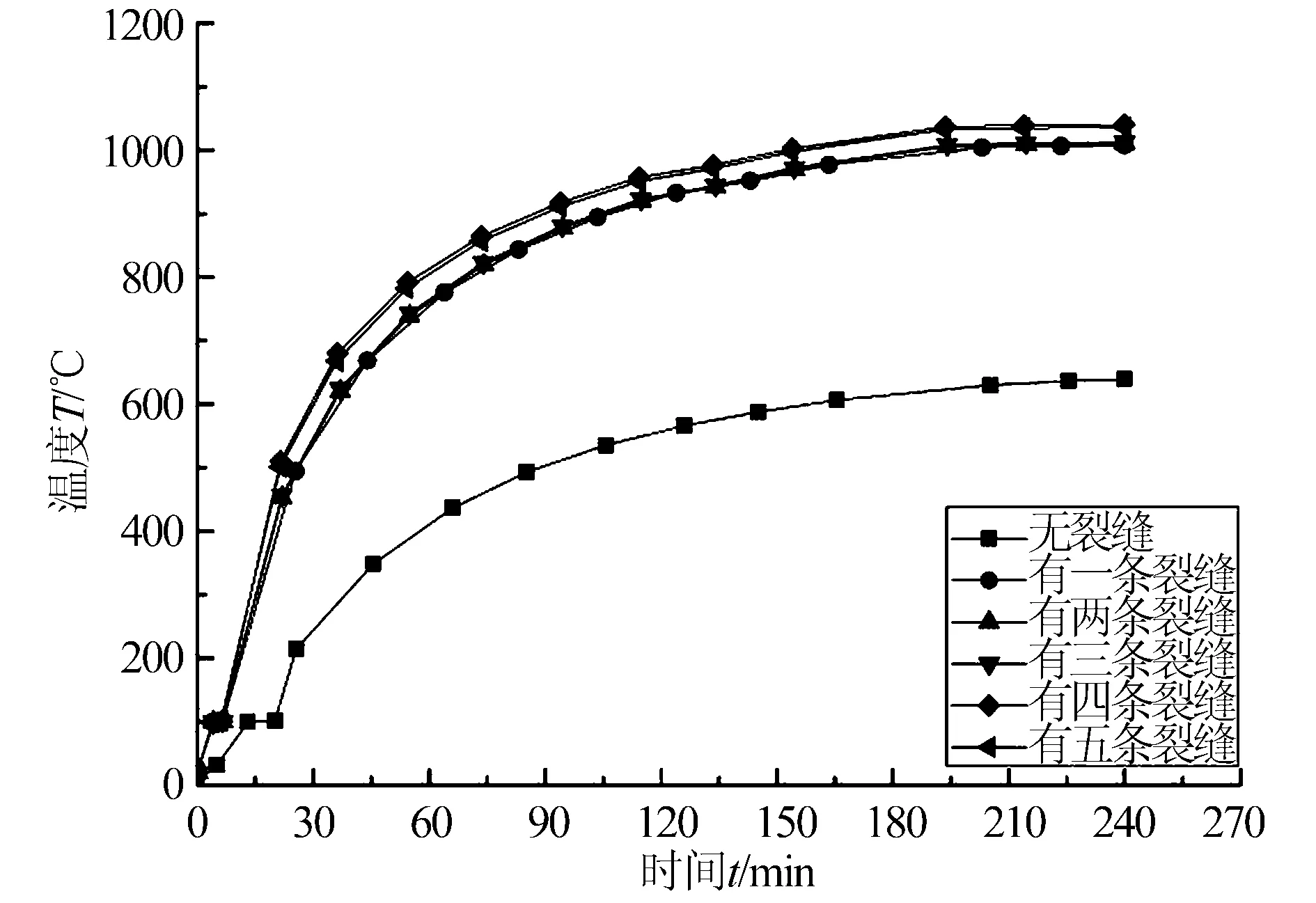
图3 点A处最高温度变化曲线图
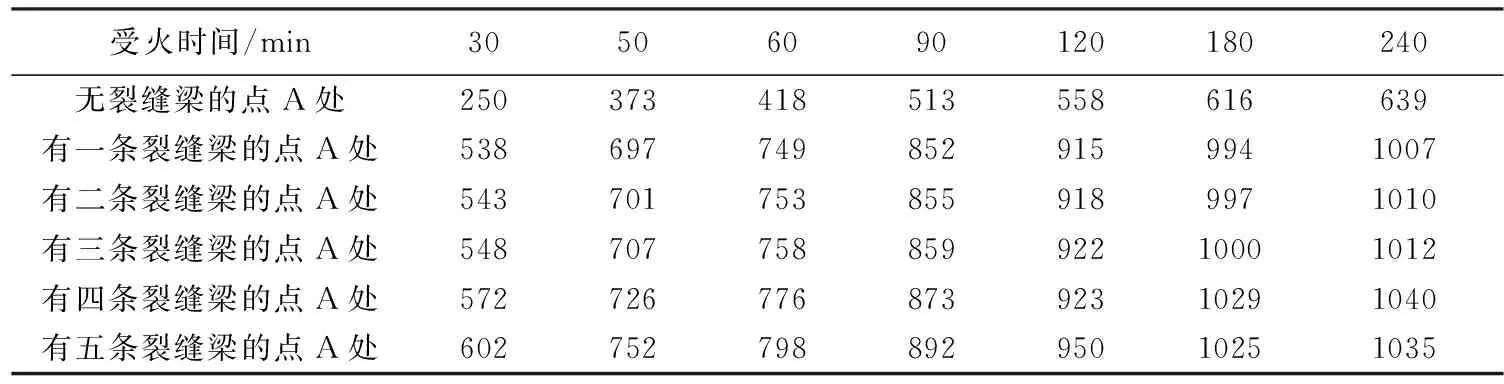
受火时间/min30506090120180240无裂缝梁的点A处250373418513558616639有一条裂缝梁的点A处5386977498529159941007有二条裂缝梁的点A处5437017538559189971010有三条裂缝梁的点A处54870775885992210001012有四条裂缝梁的点A处57272677687392310291040有五条裂缝梁的点A处60275279889295010251035
裂缝对钢筋位置的温度影响比较大,有裂缝钢筋位置的温度比无裂缝钢筋位置的温度高出55%~140%。不同裂缝条数对温度的影响不大,有五条裂缝的钢筋混凝土钢筋位置的温度比有一条裂缝的钢筋混凝土钢筋位置的温度高2.7%~11.5%。
1.4等温截面的计算方法
根据前面计算的温度场分布云状图,利用文献[6]的计算方法,得到钢筋混凝土梁300 ℃(T3)的等温线和800 ℃(T8)的等温线的位置与截面尺寸及耐火极限的关系。
当耐火极限t3=30 min时,T3的位置可用式(2)、(3)计算为
无裂缝时,b33无=b无-50h33无=h无-25
(2);
有裂缝时,b33有=b有-50h33有=h有-45
(3);
当耐火极限t5=50 min时,T3的位置可用式(4)、(5)计算为
无裂缝时,b53无=b无-70h53无=h无-45
(4)
有裂缝时,b53有=b有-70h53有=h有-65
(5)
当耐火极限t6=60 min时,T3和T8的位置可用式(6)~(9)计算为
无裂缝时,b63无=b无-90h63无=h无-55
(6)
b68无=b无-2h68无=h无-5
(7)
有裂缝时,b63有=b有-90h63有=h有-70
(8)
b68有=b有-2h68有=h有-15
(9)
当耐火极限t9=90 min时,T3和T8的位置可用式(10)~(13)计算为
无裂缝时,b93无=b无-120h93无=h无-80
(10)
b98无=b无-5h98无=h无-10
(11)
有裂缝时,b93有=b有-125h93有=h有-100
(12)
b98有=b有-5h98有=h有-25
(13)
当耐火极限t12=120 min时,T3和T8的位置可用式(14)~(17)计算为无裂缝时,b123无=b无-135h123无=h无-120
(14)
b128无=b无-15h128无=h无-10
(15)有裂缝时,b123有=b有-140h123有=h有-140
(16)
b128有=b有-15h128有=h有-35
(17)
式中:b3、b8分别为由截面300、800 ℃等温线确定的等效宽度,mm;h3、h8分别为由截面300、800 ℃等温线确定的等效高度,mm;b为柱截面宽度,mm;h为柱截面高度,mm。
1.5等温截面的简化
(1) 当无裂缝钢筋位置(点A处)的温度T1<300 ℃时。
当构件截面三面受火时,300 ℃等温线等效截面确定,其等效截面如图4所示。对于有裂缝的构件,由于裂缝的存在水平段很不明显,所以在承载力计算时忽略水平段的影响。
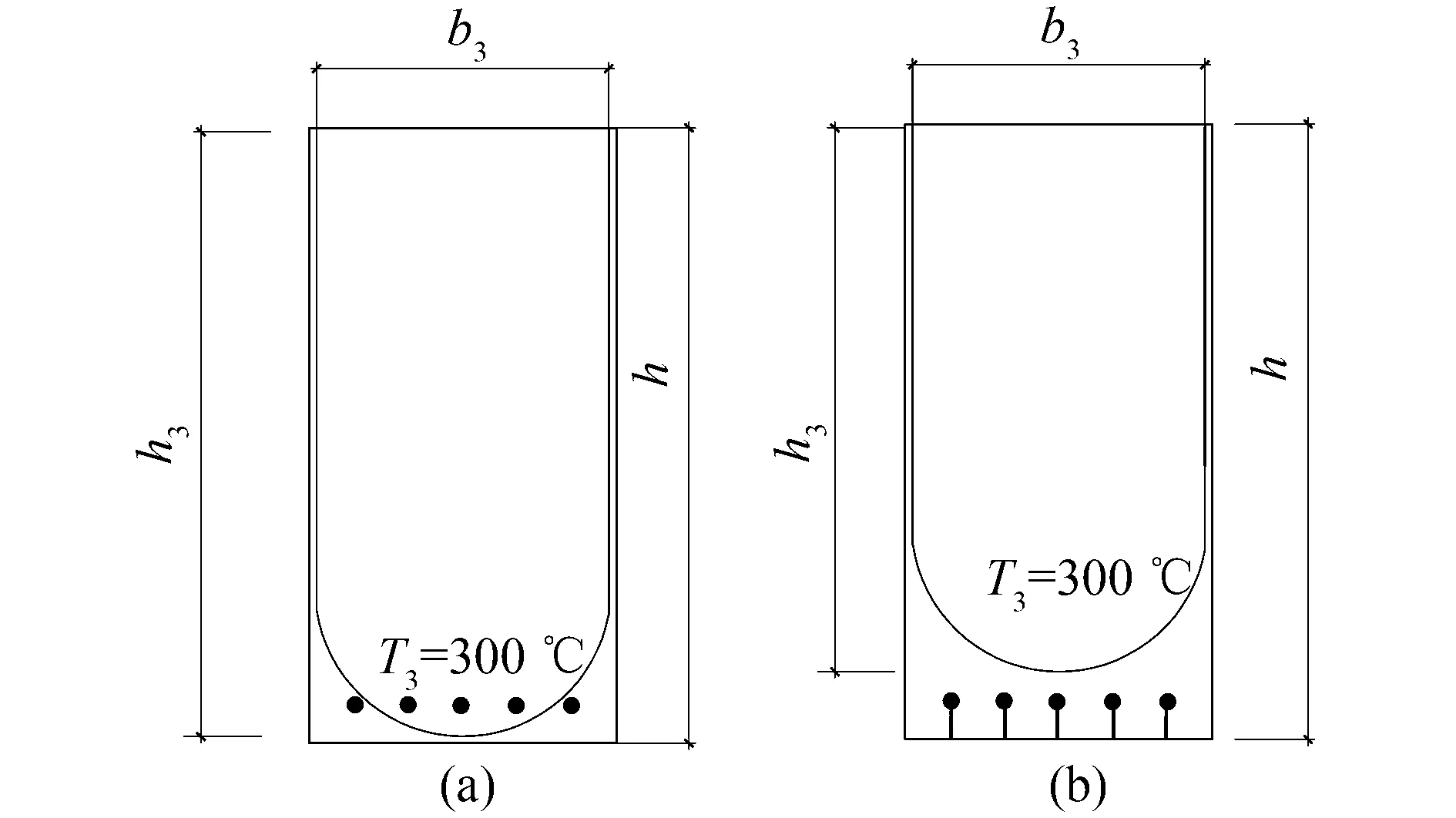
图4 无裂缝钢筋位置温度T1<300 ℃时等温线的位置图(a)无裂缝;(b)有裂缝
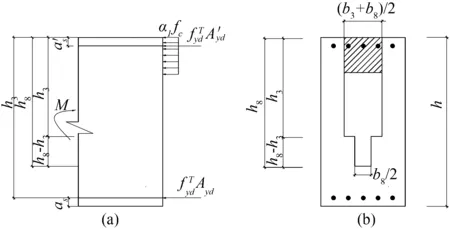
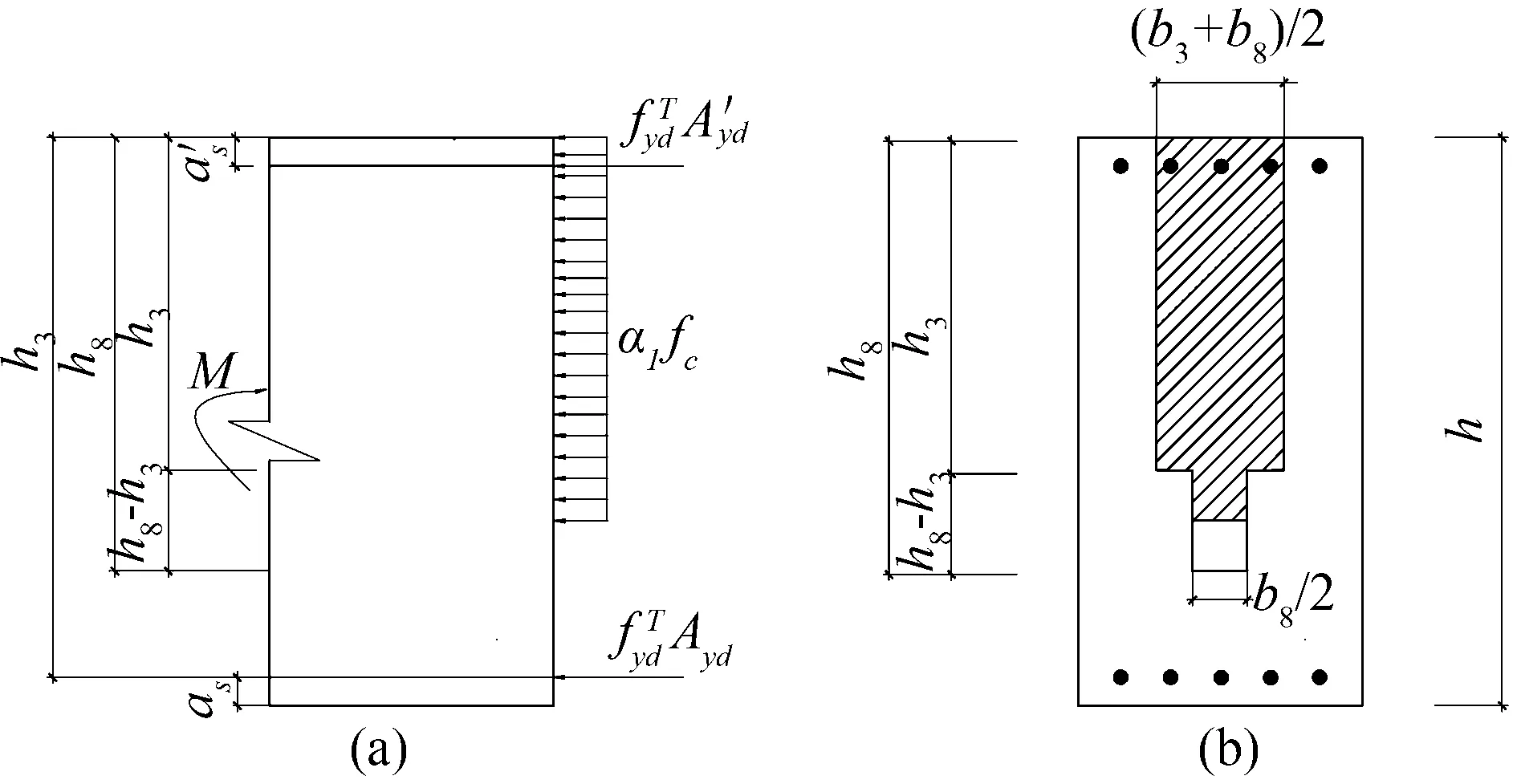
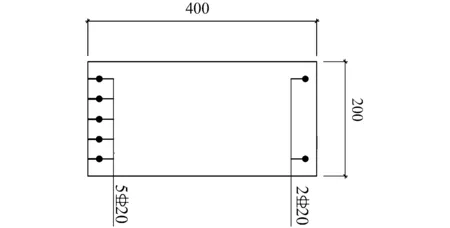
(2) 当无裂缝钢筋位置(点A处)的温度300 ℃ 当构件截面三面受火时,T3=300 ℃等温线等效截面确定,其等效截面如图5所示。 图5 无裂缝钢筋位置温度300 ℃ (3) 当无裂缝钢筋位置(点A处)的温度420 ℃ 300、800 ℃等温线等效截面确定,其等效截面如图6所示。 由此可知,由于裂缝的存在,当温度为300 ℃时,有、无裂缝钢筋混凝土的高度差为15~20 mm;当温度为800 ℃时,有、无裂缝钢筋混凝土梁的高度差为10~25 mm;在300、800 ℃温度下有、无裂缝钢筋混凝土梁的宽度差均为0~5 mm。说明裂缝对钢筋混凝土梁等效宽度影响不大,而对等效高度影响较大。 图6 无裂缝钢筋位置温度420 ℃ 根据已有的试验研究和分析可知,构件在火灾中与常温下有相似的破坏形态,所以在火灾中对于带裂缝和无裂缝的构件采用与常温下相似的假设[4-7]:(1) 截面温度场已知;(2) 截面总是保持平面,不管带裂缝还是无裂缝的梁构件截面都保持平面;(3) 钢筋和混凝土之间不产生粘结滑移;(4) 混凝土无抗拉作用。 2.1高温下钢筋的力学性能 (18) (19) (20) (21) 2.2高温下混凝土的力学性能 (22) (23) (24) 2.3带裂缝的钢筋混凝土极限承载力的计算公式 已知截面温度场分布情况,确定等温线位置,继而可得到高温等效截面。按照截面极限承载力的等效原则,将梁截面进行折减,即当温度小于300 ℃时,等效截面取全部面积;当温度大于300 ℃而小于800 ℃时,等效宽度取原截面宽度的一半;当温度大于800 ℃时,截面面积忽略不计。 根据已有的高温下无裂缝梁正截面受弯承载力计算公式[4],可以推算出带裂缝钢筋混凝土正截面受弯承载力计算公式。 (1) 受压区高度x≤h3 将原有的矩形截面简化为等效的T型截面且属于第一类情况,如图7所示,这种类型的梁的梁的有效宽度为b=(b3+b8)/2,受压区面积仍为矩形,这种情况下混凝土的受压区高度和正截面受弯承载力分别按按式(25) 、(26)计算为 (25) (26) 图7 火灾中带裂缝矩形截面构件正截面受弯承载力计算简图(x≤h3)(a) 高温带裂缝截面的极限承载力计算简图;(b)等效截面 (2) 受压区高度x≻h3 将原有的矩形截面简化为等效的T型截面且属于第二类情况,如图8所示,这种情况下混凝土的受压区高度和正截面受弯承载力分别按式(27) 、(28)计算为 (27) (28) 式中:h8为由截面800 ℃等温线确定的等效高度,mm。 图8 火灾中带裂缝矩形截面构件正截面受弯承载力计算简图(x≻h3)(a)高温带裂缝截面的极限承载力计算简图;(b)等效截面 梁截面设计参数为 混凝土:弹性模量Ec=3×104N/mm2,抗压强度设计值fc=14.3 N/mm2; 钢筋:常温下,弹性模量Es=2×105N/mm2,其屈服强度为fy=360 N/mm2; 图9 梁截面配筋图/mm 受火时间/min030无裂缝有一条裂缝有五条裂缝60无裂缝有一条裂缝有五条裂缝120无裂缝有一条裂缝有五条裂缝极限承载力/(kN·m)169.92156.2482.6468.15105.1831.126.374.1513.0911.53 由表2可以看出:当受火时间为30、60和120 min时,有五条裂缝的承载力比无裂缝的承载力分别低56%、75%和84%。当受火时间为30、60和120 min时,有五条裂缝的承载力较有一条裂缝的承载力分别低17.5%、16.4%和11.9%。总之,有裂缝的承载力比无裂缝的承载力低47%~82%,相邻裂缝之间相差11.9%~17.5%。 通过上述研究可知: (1) 通过有限元软件ABAQUS对有裂缝和无裂缝钢筋混凝土梁温度场的分析,获取在同样的受火条件下有裂缝与无裂缝的钢筋位置的温度变化规律:有裂缝钢筋位置的温度比无裂缝钢筋位置的温度高出55%~140%,有五条裂缝的钢筋混凝土钢筋位置的温度比有一条裂缝的钢筋混凝土钢筋位置的温度高2.7%~11.5%。 (2) 通过算例对有无裂缝钢筋混凝土梁极限承载力进行比较分析,得到有裂缝的承载力比无裂缝的承载力低47%~82%。 [1]王玉镯,傅传国. ABAQUS结构工程分析及实例详解[M].北京: 中国建筑工业出版社,2010. [2]吴波. 火灾后钢筋混凝土结构的力学性能[M].北京: 科学出版社,2003. [3]王玉镯. 火灾作用下(后)混凝土框架节点的力学性能分析[D].南京: 东南大学,2010. [4]杨建平,时旭东,过镇海. 高温下钢筋混凝土梁极限承载力的简化计算[J].工业建筑,2002,32(3):26-28. [5]王玉镯,范安宁,闫凯,等. 四面受热时型钢混凝土柱的简化计算方法研究[J].山东建筑大学学报,2014,29(3):214-218,224. [6]Wang Y.Z., Fu C.G.. Calculation of ultimate bearing capacity of prestressed steel reinforced concrete structure under fire [J]. Advanced Materials Research, 2011, 250-253: 2857-2860. [7]方猛. 受火灾作用钢筋混凝土受弯构件的承载力分析与简化计算[D].济南:山东建筑大学,2013. [8]刘殿魁,林敏.火灾作用下钢筋混凝土构件等效火荷载的计算[J].哈尔滨工程大学学报,2007,28(5):549-523. [9]EN 1994—1—2, The European Standard[S]. Eurocode 4: Design of Composite and Concrete Structure, Part1.2: Structural Fire Design, 2011. [10]傅传国,于德帅,王玉镯,等.预应力型钢混凝土梁火灾下抗弯承载力计算[J].山东建筑大学学报,2013,28(3)189-196. [11]傅传国,王玉镯,于德帅,等.火灾作用下预应力型钢混凝土简支梁承载性能试验研究[J].防灾减灾工程学报,2012,32(1):1-7. [12]徐杰,周晓娜,傅传国,等. 预应力型钢混凝土梁结构设计与研究[J].山东建筑大学学报,2014,29(4): 303-307. [13]傅传国,王广勇,宫梅.钢筋混凝土框架节点火灾反应非线性分析[J].山东建筑大学学报,2009,24(6):495-499. [14]傅传国,刘玮,孔唯一,等.基于升降温全曲线的钢筋混凝土梁温度场分析[J].山东建筑大学学报,2015,30(4):307-317. [15]廖杰洪,陆洲导,苏磊.火灾后混凝土梁抗剪承载力试验与有限元分析[J].同济大学学报,2013,41(6)806-812. [16]袁广林,李志奇,王勇,等.钢筋混凝土板温度场的非线性有限元分析[J].四川大学学报(工程科学版),2015,47(3):44-52. (学科责编:吴芹) Calculation method of bearing capacity of reinforced concrete beam with cracks under fire Wang Yuzhuo, Wang Cancan, Fu Chuanguo (School of Civil Engineering, Shandong Jianzhu University, Jinan 250101, China) In this paper, the capacity formulas of reinforced concrete beam with cracks under fire are proposed to study the effect of cracks on reinforced concrete structure, providing the reference for structural fire design. This paper presents a calculation method of reinforced concrete beam with cracks under fire. The temperature field calculation of the reinforced concrete beam with cracks under fire is achieved by ABAQUS. According to the results, isothermal of 300 ℃ and 800 ℃ is achieved. Combined with the calculation formula of reinforced concrete beam under the fire, the ultimate bearing capacity formulas of reinforced concrete beam with cracks are created. By using a case, the result of reinforced concrete beam with cracks and without cracks is obtained. The results indicate that the beam with cracks is 50% ~ 144% higher than that without cracks under the same conditions, and the beam with five cracks is 2.7%~11.5% higher than that with one crack. The results can be obtained that the bearing capacity of beam with cracks is 47%~82% less than that without cracks. reinforced concrete beam; fire; cracks; temperature field; ultimate bearing capacity 2015-07-04 国家自然科学基金资助项目(No.51378302);山东省科学技术发展计划项目(2013GSH2005);济南市高校院所自主创新计划项目(201303076);山东省高校科研发展计划项目(J11LE06);住房和城乡建设部科学技术项目(2013-K2-39) 王玉镯(1973-),男,副教授,博士,主要从事工程结构的抗火及防灾等方面的研究.E-mail:yuzhuowang@163.com. 1673-7644(2016)01-0007-07 TU375 A

2 高温下带裂缝钢筋混凝土梁的计算
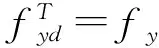
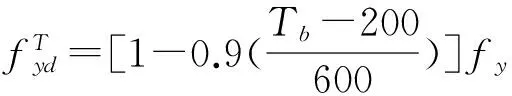
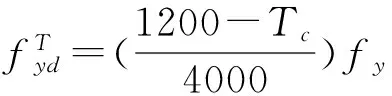
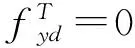
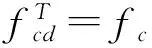
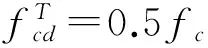
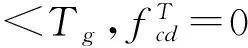
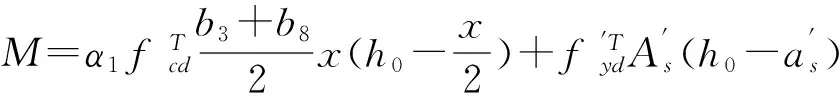
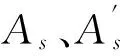
3 算例验证
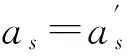
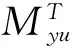

4 结论

