基于空间自相关性和模糊集的空间数据噪声点检测算法

朱付保　徐显景　白庆春　朱颢东

(郑州轻工业学院计算机与通信工程学院　河南 郑州 450002)



基于空间自相关性和模糊集的空间数据噪声点检测算法

朱付保徐显景白庆春朱颢东*

(郑州轻工业学院计算机与通信工程学院河南 郑州 450002)

大数据时代数据纷繁复杂，同时在数据挖掘过程中数据质量又至关重要，数据质量的高低将直接影响数据挖掘结果的好坏，但现实中数据缺失和噪声数据的现象在所难免。针对上述问题，通过引入空间对象的自相关性理论和模糊集理论，提出一种基于空间自相关性和模糊集的空间数据噪声点检测算法。该算法首先运用邻域对象的空间自相关性理论，计算出特定对象与邻域内其他对象的距离，进而将距离以模糊隶属度的概念予以表达，最后通过与该属性的置信水平进行比较，以此来判定噪声数据。理论分析和实验对比结果均表明，该算法对于处理空间数据噪声点问题是有效可行的。

噪声数据数据预处理空间自相关性模糊集

0　引　言

随着空间数据在社会、生活等各方面应用的深入，从空间数据库中自动或半自动地挖掘隐藏的关系模式，进而根据现有关系模式预测空间对象未来可能发生的行为已变得更具价值。伴随着大数据时代的到来，如何从大数据中提炼出大价值已成为数据挖掘领域研究的重点[1]。与此同时，数据的质量也变得尤为重要，数据预处理则是数据挖掘过程中一个重要步骤和数据质量提升的关键手段[2]。空间数据挖掘相较于传统的数据挖掘具有更为复杂的数据特点，空间数据都不是孤零零的存在，一种事物总是与其他事物相关联，而且距离相近的事物其相关性要大于距离较远的事物，因此在特定的应用领域要更加注重空间数据对象间的自相关性问题。在大数据时代，数据类型更加多样，规模更为庞大，数据间的关联也更为复杂。在数据挖掘过程中，如果缺失数据处理不当，那么与之相关的有价值的知识也常常会被忽略[3]。大而低质量的数据有时不仅不能支撑有效的数据挖掘，反而还会给数据挖掘的结果造成不同程度的干扰，简单地认为数据越多越好而不关心数据的质量会使得挖掘的结果变得难以预料[4]。

但是在现实世界中，由于人为的或自然的因素造成的数据缺失或噪声数据在所难免，噪声数据或缺失数据不可避免地会对空间数据挖掘的结果产生影响。在这方面许多人都曾做过比较深入的研究，文献[5]对传统的数据质量评估方法和数据质量提高技术做了分析比较，文献[6]则着重分析了领域无关的数据清洗的特点，并对相关方法进行了分类介绍。异常数据检测主要可以分为四类：基于分布、基于聚类、基于距离和基于密度的方法[7]。文献[8]提出了基于空间局部偏离因子的离群点检测算法，该算法运用空间局部偏离因子来衡量离群点问题，但对于给定对象邻域范围的定义采用的是对象的非空间属性带权距离小于特定值k的所有空间邻居的集合，没能充分利用空间对象在空间位置上的自相关性特点，而且在数据量大的情况下会造成很大的计算压力。

为了有效控制数据质量，提高检测的准确率和效率，本文通过研究空间数据的自相关性理论和模糊集理论在解决模糊问题方面的优势，提出基于空间自相关性和模糊集的空间数据噪声点检测算法。该算法对空间数据离群点的度量方式进行了进一步的改进，以空间对象的空间位置作为对象邻域划定的标准，进而将该对象对于领域内其他对象的隶属度和置信水平进行比较判定该对象的可靠性。

1　空间数据消噪模型

模糊集理论认为元素总是以一定的程度隶属于某一集合，也可能是以不同的程度隶属于多个集合，而非经典数学中的二元性，使得元素的隶属度概念具有一种亦此亦彼的模糊性[9,10]。空间自相关描述的是一些变量在同一个分布区内的观测数据之间潜在的相互依赖性关系。地理学第一定律指出任何事物与其他事物之间都是相关联的，同时距离较近的事物比距离较远的事物的关联性更强[11,12]。对于空间数据库而言，因为包含大量的空间信息，因此各数据元素之间的相关度比一般的业务型数据库中数据的相关度更大，相互联系更为紧密。本文据此提出了基于空间自相关性和模糊集理论的空间数据消噪模型。首先，计算指定对象与其邻域内其他对象的平均距离；其次，在相似性概念的基础上引入模糊集理论，在特定对象与邻域内其他对象平均距离的基础上定义其与领域内其他对象相似度的隶属度函数；再次，根据计算所得的隶属度与置信水平进行比较，在置信水平之内认定为可靠性数据，置信水平之外则认为是非可靠性数据；最后，依据对数据属性的可靠性判断，对非可靠性数据进行消噪处理。

在数据消噪处理过程中最重要而且最核心的问题是对数据噪声点的检测，所谓数据噪声点指的是在数据集中与整体数据集或局部数据集有显著异常或表现不一致的数据观测点[13]，本文基于空间自相关性和模糊集理论来进行噪声点数据的判定。

空间对象的属性数据与邻域内相应属性数据的距离，可以有效地表达数据对于邻域数据的融入度。属性空间中对象与邻域空间内其他对象的距离越小，说明越相似，进而表明对象的数据可靠性越高；距离越大，表明对象与邻域空间内其他对象的差异越大，进而说明该数据的可靠性越低，出现错误的可能性就越大。设包含N个空间对象{O1,O2,…,ON}的空间数据集O，每个空间对象Oi具有M个可度量特征属性Oi={Oi1,Oi2,…,OiM}，对象Oi的第k个特征属性与其邻域内对象Oj的第k个特征属性的平均距离定义为：

(1)

(2)

(3)

2　基于自相关性和模糊集的空间数据消噪算法

2.1算法描述

通过对空间消噪模型的定义说明，基于空间自相关性和模糊集理论的空间数据消噪算法描述如下：

1) 初始化空间对象集合O，针对空间对象的M个可度量特征属性，分别为每个属性设置对应的邻域半径r、可靠性系数C和置信水平λ，以3*M的二维数组Arr形式存储；

2) 将空间对象集合O中的所有对象投影到二维平面上；

3)FORi=1ToO.Length；

4)FORk=1ToM；

5) 令r=Arr[0][k-1]，C=Arr[1][k-1]，λ=Arr[2][k-1]；

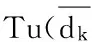
9)ELSE;

10)Continue;

11)ENDFOR;

12)ENDFOR;

2.2参数控制说明

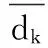
3　实验结果与分析

根据上文介绍的算法思想，本文以某机场及其附近地区2003年至2009年各监测点利用永久散射体点(PS)监测到的地面沉降量数据为例进行实验。实验的软件环境是：MicrosoftWindows7操作系统；MicrosoftSQLServer2008数据库；Microsoft.NETFramework4.0；算法的实现语言为C#。

实验选取数据集中的经度、纬度和年均沉降量3个属性进行，数据量为39 195条，在此数据集中随机加入240条噪声数据组成新的数据集，实验中以数据噪声点检测率和噪声点检测的错检率来度量算法的准确性。实验结果如表1所示。

表1　噪声数据检测结果

从表1中的实验结果可以看出，本文提出的算法相对于整个数据集而言具有检测率高、错检率低的特点。同时，可靠性系数C和置信水平λ对数据噪声点检测的结果影响比较明显，在同一数据集的基础上，可靠性系数和置信水平的改变会相应地改变所检测到的噪声点数据的数量，因此运用该算法进行空间数据消噪处理时，需要根据数据的特性选择合适的可靠性系数和置信水平。

为了进一步验证本文所提出算法的有效性，本文算法与LOF算法、SLDF算法分别从正检率、错检率和算法执行时间三个方面进行了对比，对比结果如表2所示。实验结果表明，在相同情况下，本文所提算法在检测率和算法执行时间方面都要优于LOF算法和SLDF算法，并且适用于数据集规模较大的空间数据检测。

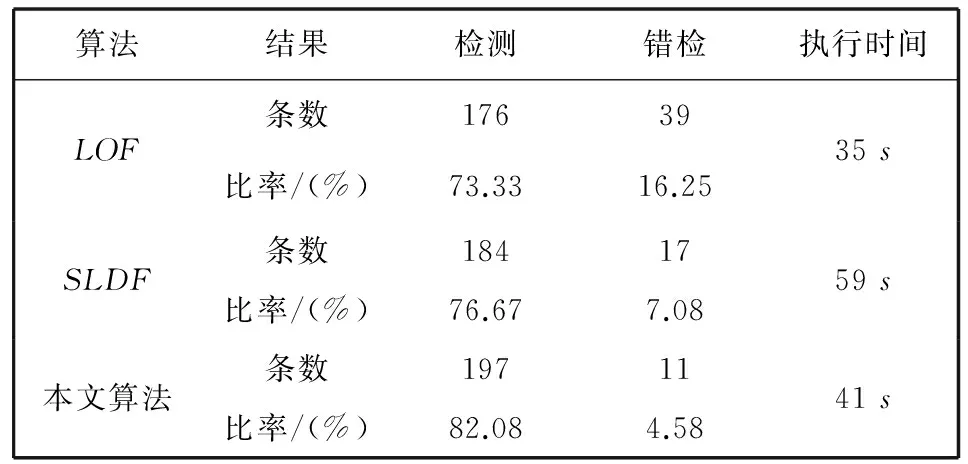
表2　实验结果对比

4　结　语

针对空间数据具有自相关性的特点和模糊集在解决模糊问题方面的优势，本文提出了一种基于空间自相关性和模糊集理论的空间数据噪声点检测算法。该算法主要利用空间数据的自相关性，对数据对象的离群度度量方式进行了进一步改进，将对于某一点数据对象的判定借助于其邻域内其他的数据对象来进行，进而通过可靠性系数得出该点相对于邻域对象的隶属度关系，通过隶属度与置信度水平来检测空间数据库中可能存在的噪声点数据。将该算法在实验数据集上进行相关实验，并与文献[14]的LOF算法和文献[8]的SLDF算法分别进行比较。理论分析与实验结果表明，本文算法在检测较大规模空间数据集的噪声点问题时，具有较高的效率和准确率。

[1] 王树良,丁刚毅,钟鸣.大数据下的空间数据挖掘思考[J].中国电子科学研究院学报,2013,8(1):8-17.

[2] 汪伟,邹璇,詹雪.论数据挖掘中的数据预处理技术[J].煤炭技术,2013,32(5):152-153.

[3] 武森,冯小东,单志广.基于不完备数据聚类的缺失数据填补方法[J].计算机学报,2012,35(8):1727-1737.

[4] 靳小龙,王元卓,程学旗.大数据的研究体系与现状[J].信息通信技术,2013,7(6):35-42.

[5] 韩京宇,徐立臻,董逸生.数据质量研究综述[J].计算机科学,2008,35(2):1-5.

[6] 曹建军,刁兴春,汪挺,等.领域无关数据清洗研究综述[J].计算机科学,2010,37(5):26-29.

[7] 薛安荣,姚林.离群点挖掘方法综述[J].计算机科学,2008,35(11):13-18.

[8] 张天佑,王小玲.基于空间局部偏离因子的离群点检测算法[J].计算机工程,2011,37(14):282-284.

[9]PrzemysawGrzegorzewski.Onpossibleandnecessaryinclusionofintuitionisticfuzzysets[J].InformationSciences,2011,181(2):342-350.

[10] 赵立权.模糊集、粗糙集和商空间理论的比较研究[J].计算机工程,2011,37(2):22-24.

[11]DanielaStojanova,MichelangeloCeci,AnnalisaAppice,etal.Dealingwithspatialautocorrelationwhenlearningpredictiveclusteringtrees[J].EcologicalInformatics,2013,13(1):22-39.

[12]XiQu,LungfeiLee.LMtestsforspatialcorrelationinspatialmodelswithlimiteddependentvariables[J].RegionalScienceandUrbanEconomics,2012,42(3):430-445.

[13] 王伟一,郝文宁,赵水宁,等.基于相对密度的军事高维数据噪声点检测方法[J].计算机工程,2009,35(5):50-52.

[14]BreunigMM,KriegelHP,NgRT,etal.LOF:IdentifyingDensity-basedLocalOutliers[C]//Proc.ofACMSIGMODConference.NewYork,USA:ACMPress,2000:427-438.

SPATIALDATANOISEDETECTIONALGORITHMBASEDONSPATIALAUTO-CORRELATIONANDFUZZYSET

ZhuFubaoXuXianjingBaiQingchunZhuHaodong*

(School of Computer and Communication Engineering,Zhengzhou University of Light Industry,Zhengzhou 450002,Henan,China)

Datashowsmorecomplexcharacteristicsintheeraofbigdata.Meanwhile,thequalityofdataiscrucialintheprocessofdataminingandwilldirectlyaffecttheresultsofdatamining,butthephenomenaofdatamissingandnoisedataareinevitableinreality.Aimingattheaboveproblems,byintroducingthetheoryofspatialauto-correlationofspatialobjectandthetheoryoffuzzysetweproposeaspatialdatanoisepointdetectionalgorithm.First,thealgorithmcalculatesthedistancebetweenthespecificobjectandotherobjectswithinitsneighbourhoodbyusingspatialauto-correlationtheoryofneighbourhoodobject.Thenitexpressesthedistancebytheconceptoffuzzymembershipdegree.Finally,itdetermineswhetherthereisanoisedatabycomparingwiththeconfidenceleveloftheattribute.Theoreticalanalysisandexperimentalcomparisonresultsallshowthatthismethodiseffectiveandfeasibleinhandlingtheproblemofspatialdatanoisepoint.

NoisedataDataprepossessingSpatialauto-correlationFuzzyset

2014-08-09。国家自然科学基金项目(61201447)；河南省科技攻关项目(122102210492)；河南省教育厅科学技术研究重点项目(13A520368，13A520367)。朱付保，副教授，主研领域：智能信息处理，空间数据库。徐显景，硕士生。白庆春，硕士生。朱颢东，副教授。

TP315

ADOI:10.3969/j.issn.1000-386x.2016.03.062