轨道客车随机振动精细分析方法
刘晓雪,郭翰飞,佟维,张有为
(1.大连交通大学 交通运输工程学院,辽宁 大连 116028; 2.大连理工大学 运载工程与力学学部,辽宁 大连 116024; 3. 大连交通大学 机械工程学院,辽宁 大连 116028)*
轨道客车随机振动精细分析方法
刘晓雪1,2,郭翰飞3,佟维1,张有为2
(1.大连交通大学 交通运输工程学院,辽宁 大连 116028; 2.大连理工大学 运载工程与力学学部,辽宁 大连 116024; 3. 大连交通大学 机械工程学院,辽宁 大连 116028)*
建立了轨道客车结构随机振动精细分析计算方法和工程应用系统.将求解随机振动的虚拟激励法与分体耦合式振型分解法相结合,大幅提高了结构随机振动分析计算的效率,使车辆动力学计算模型与静强度分析模型的规模有相同量级;有效地处理了比例阻尼和非比例阻尼共存同一模型的复杂阻尼体系,保证数值计算精度.可采用有限元法建立车辆整体结构动力学精细模型,以轨道不平顺谱作为输入激励载荷,进行随机振动仿真计算,除了将车辆运行平稳性的评价精度从“体”提高到“点”外,可以直接进行结构随机应力计算和疲劳寿命评估,从而形成车辆结构全生命周期的完整仿真体系.开发了工程应用系统,并通过工程实例证明方法和应用系统的有效性.实例给出25T型客车详细的结构随机振动响应分布,表明利用该系统可以揭示轨道客车结构任意部位的动态行为和减振效果,扩展了现行车辆系统动力学功能.
精细分析;虚拟激励法;随机振动;轨道车辆
0 引言
传统车辆动力学采用多刚体动力学为基础的简化模型,忽略车体、构架等结构件内部弹性、阻尼和质量分布.由于模型的粗糙,弱化了车辆动力学应有的功能,对于现代车辆设计来说有以下不足:①不能通过计算获得部件的局部振动详细信息,特别是相对高频部分,从而使局部结构改动对动力学指标的影响很不敏感,相关数据只能在实际样车造出后,通过现场试验测得;②受电弓、空调及气动力等载荷难以施加,而这些载荷对局部结构振动的影响不可轻视;③计算结果不适用于作为基础数据进行疲劳预测、噪声分析等需要详细信息的工程问题研究.要真正解决上述问题,在设计中确切掌握随机性动载荷作用下车辆结构的详细振动状态是关键.因此,开发随机振动精细分析方法是轨道车辆动力学领域的重要课题[1].近年来,国内外学者不断探讨包含车辆部件弹性的车辆动力学分析方法,归纳起来有将车体用梁单元模拟的随机振动分析、谐振分析、振动模态分析和采用刚柔混合模型的多体动力学分析等4类.其中,将车体用梁单元模拟的随机振动分析和谐振分析一般用于专题研究,不能用于定量评价[2];模态分析已经被广泛应用,是从振动特性的角度对结构提出要求,在某种程度上代替对车体振动指标的评价[3];采用刚柔混合模型的多体动力学是近年来被研究开发最多的方法[4- 5],它将部件变形的影响在某种程度上纳入振动分析中,使求解精度有所提高,但本质上未能超越多刚体动力学的基础.总之,上述方法各有特点,但均没有从根本上解决轨道车辆随机振动精细分析问题[6- 7].
本文从提高轨道客车结构随机振动分析计算效率入手,利用解随机过程的虚拟激励法[6]与求解结构振动的振型分解法结合作为基础方法,开发了车辆结构随机振动精细分析的计算方法和应用仿真系统.所谓精细是指,车辆动力学模型用有限元方法建立,其网格大小与目前静应力计算同一量级,不但可以计算车辆结构任意点的位移、速度和加速度,而且能获得足够精度的随机应力信息.并通过工程实例证明了本文方法和应用系统的有效性[8- 9].
1 车辆系统振动特点与精细计算思路
1.1基本受力分析
轨道车辆的主要结构由车体、转向架、轮对等部件组合而成.对于现代客车,车体通过中央弹簧阻尼系统(称二系悬挂装置)落在转向架构架上,构架通过轴箱弹簧阻尼系统(称一系悬挂装置)落在轴箱及轮轴上,结构系统简图如图1所示.其结构动力学方程为:

(1)
式中:x(t)为随时间变化的位移;M、C、K常量系数分别为质量、阻尼和刚度;F(t)为随时间变化的载荷.当方程为多自由度体系时,上述各量均为矩阵形式.

图1 轨道客车结构简图
1.2两个主要特点
(1)载荷的随机性
由于轨道车辆动力学系统的载荷主要来自具有随机特性的轨道不平顺、车钩载荷和风载荷,所以轨道车辆振动行为是随机过程.根据随机振动理论[10],对于受平稳随机激励的线性系统,方程(1)的响应x(t)的自谱密度Sxx(ω)为
(2)
其中:H(ω)为频率响应函数;SFF(ω)为随机载荷F(t)的自谱密度.如果自由度数为n,频率响应函数H(ω)为n×n阶矩阵.常规计算Sxx(ω)首先求出H(ω)矩阵,然后进行矩阵相乘.所以,当问题规模较大时,式(2)的计算求解量极大,虽然随机振动理论早已建立,但解题规模有限,对于工程问题必须做大幅度简化后才能求解.计算效率低,成为制约轨道车辆等大型结构随机振动分析的瓶颈.
(2)刚度和阻尼的不均匀性
车辆主要部件(车体、构架、轮轴等)结构与两系悬挂装置相比,刚度大、阻尼小,而且数值相差较大,属于刚度、阻尼不均匀的振动系统.对此类系统运用数值方法求解,往往会产生不同程度的奇异,影响计算精度.
以上两点也是车辆动力学采用多刚体动力学建立模型体系的主要原因.
1.3精细计算方法思路
认为轨道车辆振动为受多点(轮轨接触点)完全相干平稳随机激励的线性平稳随机过程,悬挂装置的各类弹簧和阻尼(减振器)为线性.
计算模型完整(包括车体、转向架、轮对及弹簧悬挂等),且能够描述足够的结构细节,是实现轨道车辆随机振动精细分析的基本要求,意味着动力学模型必需具有相当的规模.就目前的数值方法和计算工具而言,建立精细分析模型不难,可以采用已经广泛应用的有限元法,解决问题的关键是提高计算效率.
为此,本文从两方面入手:
(1)结构动力学计算采用振型分解法,它被证明解大规模结构振动问题是行之有效的,并根据车辆结构特点采用分体耦合方式;
(2)随机过程求解采用虚拟激励法,将计算效率提高3~4个数量级[10].有了高效的计算能力,就可以采用有足够信息量的精细模型,从而获得详细的随机响应,实现轨道客车结构随机振动仿真从“体”到“点”的进步.具体技术路线如图2所示.
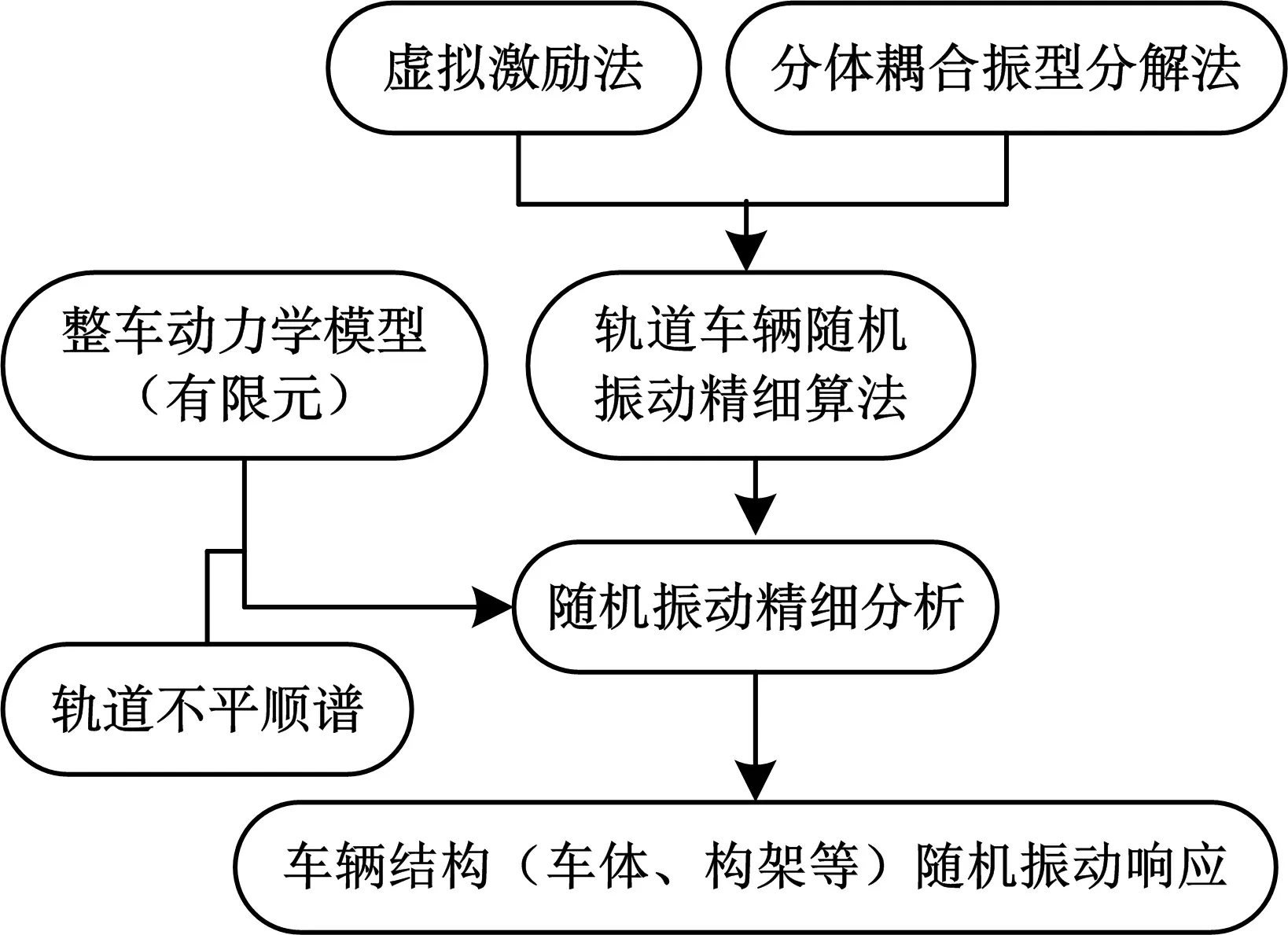
图2 轨道车辆随机振动精细分析方法技术路线简图
2 分体耦合式振型分解法
将车辆结构按车体、构架和轮对3个部件采用有限元法分别建立动力学方程,方程右端项为部件间作用力,通过部件间作用力建立耦合关系.
车体
(3a)
构架
(3b)
轮对
(3c)
其中:下标c、t、w分别表示车体、构架、轮对;下标为两个字母的表示两个部件之间相互作用关系,第一下标表示作用点在这一部件上,第二下标表示相连的另一部件;
为二系悬挂装置(车体与构架间)作用力;
为二系悬挂装置(构架与轮对间)作用力;Fwr=Kwr(ur-xw)为轮轨作用力;
ur为具有随机性质的轨道不平顺(包括高低、方向、轨距、水平四种);Kwr为轮轨接触相当刚度[7];Cs1、Cs2分别为悬挂装置的阻尼(下标s1、s2分别表示该元件属一系悬挂装置还是二系悬挂装置);Ks1、Ks2分别为悬挂装置的刚度(下标s1、s2意义同上).
建立动力学方程组后,对各部件分别实施振型分解法.将xv(v=c,t,w)用各自前q阶振型的组合表示,即
(4)

(5)
方程(5)为二阶线性常微分方程.如果是通常的铁路客车(模型包括1个车体、2个构架和4个轮对,共7个部件),方程(7)为7×q个独立的动力学方程,右端项Fr中的非零元素为轮轨接触点的随机不平顺等载荷谱.
3 基于虚拟激励法的随机振动分析
根据文献[10]针对方程(5)实施虚拟激励法解随机振动响应.
首先构造虚拟激励
(6)

l1为构架轴距,l2为车辆定距,v车辆运行速度.

(7)

根据结构动力学理论解此方程求得虚拟主坐标
(8)
其中频响函数
(9)
使虚拟位移相乘得
(10)
其中:‘*’表示复共轭,得到与式(2)相同的真实位移响应功率谱.将随机振动分析求解响应功率谱的问题,转化为简谐振动分析问题求解.在精度不变的情况下,较之传统计算方法免去了求解频响函数矩阵和矩阵连乘的大量运算.这个方法特别适用于工程实际问题,模型规模越大,计算效率的优势越明显.
4 工程实例
为了检验上述方法和应用程序系统的有效性,对国产25T型提速软卧客车进行了随机振动精细分析.
4.1计算模型
25T型提速软卧客车为碳钢材料,传统的骨架蒙皮式结构,采用国产CW- 200型转向架,最高运行速度160km/h,按照生产企业提供的工程图建立整车动力学模型(包括车体、构架轮对结构及两系悬挂系统)如图3所示.其中3(a)为整体结构模型图,3(b)为构架网格.模型节点总数为979 163个,其中,车体414 213个,构架153 803个,轮对64 336,自由度数约20万.分别对车体、构架、轮对等部件进行模态分析,取前100阶振型作为输入数据,截取频率范围各部件不同,其中车体33Hz、构架421Hz、轮对5 915Hz,可以保证部件在低阶段的主要振型不被漏掉.

(a)车体有限元模型

(b)构架有限元模型

(c)轮对有限元模型
激励载荷为轮轨接触点的轨道随机不平顺谱.考虑到目前我国的相关标准中尚未包含具体载荷谱,本文采用美国AAR标准提供的六级轨道谱,施加在车轮的轮轨接触点,离散为1 000个采样点.
4.2结果分析
计算得到25T型客车结构详细的随机振动响应数据.下面仅对计算效率和部分计算结果进行考察.
4.2.1计算效率
计算耗时23 min左右,其中,大部分时间用于模态分析、数据传输和计算结果图形化过程.关于图3所示模型网格的疏密程度,单纯的动力学分析已经足够,但是作为能够反映应力集中的动应力分析还显粗糙.为了进一步考察计算规模和速度,我们将结构模型加大到130万个自由度,全部计算用时83 min.这样的解题规模(模型网格密度)与当前轨道车辆结构静应力计算处在相同的量级,计算时间完全可以接受,实现了在普通微机上进行车辆结构随机振动精细分析的目的.
4.2.2构架振动分析
在轨道车辆领域习惯将振动按照垂向、横向和纵向分解表达,因篇幅有限,不能全部介绍,这里只给出构架垂向和横向随机振动分析.
为了清楚表达结构加速度功率谱的分布,设计了两种形式的功率谱图.一种是用三维直角坐标表达连续结构的 “线图”(如图4(a)所示),其中一个水平轴为结构,另一水平轴为频率,垂向轴为功率谱;另一种是二维直角坐标表达结构离散点的 “点图”(如图4(b)所示),图中横轴为频率,纵轴为加速度功率谱密度值.图4(a)为构架侧梁的加速度功率谱分布.从频率看,振动能量主要分布在5 ~100 Hz之间,40~90 Hz是比较集中的频段,几个峰值都在10以上,最大在60~70 Hz的范围,峰值达26.从结构上看,加速度功率谱值分布可分为两个区,一个是侧梁端部(轴箱弹簧处)到与横梁交点,为迅速衰减区,其峰值大约下降90%以上;另一个是从与横梁交点到中点(空气弹簧处),是保持较低水平振动的区段.
为了便于比较,图4(b)给出侧梁端部、横梁连接处和中间位置这三个特征点的加速度功率谱.根据多年的经验和掌握的运行试验数据(笔者2005年曾组织实施了该车在京广线的动力学试验),认为计算结果无论是量级还是分布规律都符合实际情况.

(a)节点选取示意图

(b)垂向加速度功率谱

(c)横向加速度功率谱

(d)侧梁三个位置的垂向加速度功率谱
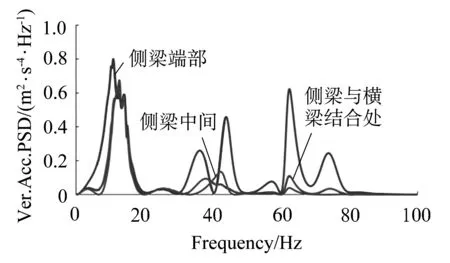
(e)侧梁三个位置的横向加速度功率谱
由此可见,本文方法能够获得足够的仿真信息,详细给出构架随机振动能量分布,清晰的表达了构架在车辆系统中的减振作用,实现了轨道车辆动力学仿真计算精细程度从“体”级到“点”级的进步.
5 结论
(1)打破了轨道客车结构系统随机振动分析计算效率低下的瓶颈,其模型的规模与静强度分析有相同的级别(自由度数达百万级),实现了精细分析之目的;
(2)有效的处理比例阻尼和非比例阻尼共存、部件间刚度相差较大的复杂振动体系,保证数值计算精度;
(3)开发的轨道客车随机振动精细分析应用系统达到预期目标,能够在设计阶段(造出物理样车之前)通过数值仿真技术对机车车辆结构进行任意部位的随机响应分析,扩大了车辆动力学的应用范围;
(4)算例给出25T型软卧客车构架随机振动响应分布规律,40~90 Hz是比较集中的频段;详细揭示了构架的减振作用,可将一系悬挂装置传来的激扰衰减90%左右.为设计提供精确的参考,大幅提高了动力学仿真在车辆设计中的参考价值;
(5)由于模型的精细程度能够反映应力集中(与静强度模型同量级),可进一步求得作为结构疲劳评价基础数据的随机应力,为实现轨道车辆全生命周期的设计理念提供强有力的支持.
[1]金学松,温泽峰,张卫华,等.世界铁路发展状况及其关键力学问题[J].工程力学,2004(增刊1):90- 104.
[2]李世亮.计及车体弹性效应的车辆动力学振动方程、振型函数和频率方程解析[J].铁道车辆,1998,36(7):9- 12.
[3]王开云,蔡成标,徐志胜.基于频域方法的轨道随机振动特性及试验验证分析[J].机械工程学报,2005,41(11):149- 152.
[4]程海涛,王成国,钱立新.考虑车体柔性的货车动力学仿真[J].铁道学报,2000,22(6):40- 45.
[5]任尊松,孙守光,刘志明.构架作弹性体处理时的客车系统动力学仿真[J].铁道学报,2000,24(6):31- 35.
[6]陈果.车辆轨道耦合系统随机振动分析[D].成都:西南交通大学,2000.
[7]TD LE,KK AHN.A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat[J].Journal of Sound and Vibration,2011,330(26):6311- 6335.
[8]佟维,王帝,郭翰飞,等.25T型软卧车结构随机振动精细分析[J].大连交通大学学报,2013,34(5):58- 62.
[9]郭翰飞,刘晓雪,佟维,等.高速检测车车下BTM吊装座随机应力分析[J].大连交通大学学报,2014,35(增刊1):17- 21.
[10]林家浩,张亚辉.随机振动的虚拟激励法[M].北京:科学出版社,2004:42- 58.
An Accurate Method of Railway Vehicles Random Vibration Analysis
LIU Xiaoxue1,2,GUO Hanfei3,TONG Wei1,ZHANG Youwei2
(1.School of Traffic & Transportation Engineering,Dalian Jiaotong University,Dalian 116028,China; 2.Faculty of Vehicle Engineering and Mechanics,Dalian University of Technology,Dalian 116024,China; 3.School of Mechanical Engineering,Dalian Jiaotong University,Dalian 116028,China)
An accurate method of railway vehicles random vibration analysis and engineering application systems are established. Pseudo excitation and mode decomposition methods are coupled to improve the efficiency of analysis which make vehicle dynamics model with the static strength analysis model has the same order of magnitude. Proportional damping and non-proportional damping models coexisted in the same complex damping system are effectively handled. Finite element method is used to establish the vehicle dynamic accurate model, and track irregularity spectrum is employed to calculate excitation loads, the random structural stress and fatigue life of every point. A complete simulation system life cycle of the vehicle structure is formed. Engineering applications is developed, and the effectiveness of the method and application systems is demonstrated. 25T vehicle structural distributed random vibration response is given as example to indicate the use of the system to give the dynamic behavior and structural damping effect of the railway vehicles and extend the vehicle system dynamics.
accurate analysis method; pseudo excitation method; random vibration; railway vehicles
1673- 9590(2016)05- 0036- 06
2016- 06- 10
国家自然科学基金资助项目(11402043)
刘晓雪(1982-),女,讲师,博士研究生,主要从事车辆结构随机振动的研究
E-mail:snow_228@djtu.edu.cn.
A

